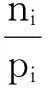关于Q值法的一种改进
王 颖
(安徽科技学院 数理与信息工程学院,安徽 滁州 233100)
浙江科技学院学报,第27卷第1期,2015年2月
Journal of Zhejiang University of Science and Technology
Vol.27 No.1, Feb. 2015

关于Q值法的一种改进
王颖
(安徽科技学院 数理与信息工程学院,安徽 滁州 233100)
摘要:Q值法是处理席位公平分配问题的一种简便实用的方法。通过分析Q值法和新Q值法的优缺点,借鉴它们的思想,对相对不公平度的度量问题进行了探讨;并在此基础上给出了新的相对不公平度的定义及计算Q值的简易算法,同时结合实例对3种方法进行了对比分析,进而揭示了三者之间的联系与区别,认为新方法避免了已有Q值法的一些缺陷,相对更为合理。
关键词:相对不公平度;Q值法;席位公平分配
席位公平分配研究的是一类资源分配问题,在管理和对策论等众多领域具有广泛的应用价值。在处理这个问题时,早期使用的是尾数最大法,后来又陆续采用了Q值法[1-3]、D’Hondt法、新Q值法[4]、最大熵法[5]、判别数法、最小极差法及最大概率法等。然而,由于席位分配问题的复杂性,很多情况下并不存在绝对公平的分配方法。笔者通过对Q值法和新Q值法的比较研究,参照它们对相对不公平度的定义,给出了相对不公平度的新定义,并在此基础上提出了较简单合理的Q值计算方法。
1经典Q值法和新Q值法的评价
1.1 问题的一般表述
设m方共P人参与总席位数为N的分配,第i方的人数为pi(i=1,2,…,m),记第i方分配到的席位数为ni,试问ni是多少?
例如,设某学院有3个系共200名学生,其中甲系103名、乙系63名、丙系34名。现召开学生代表会议,设21个席位,试确定公平合理的席位分配方案。
对于这种问题,通常的做法是按人数比例分配席位,当出现小数时采用尾数最大法。但是实践表明,这种比例加惯例的分配方法在很多情况下并不一定公平合理,因而出现了很多其他方法,本研究仅就Q值法进行详细讨论。
1.2 经典Q值法
设A、B两方人数分别为p1和p2,占有的席位分别为n1和n2,当p1/n1>p2/n2时,经典Q值法定义对A方的相对不公平度为

(1)
当总席位增加1席时,根据公平的席位分配方法应该使得相对不公平度尽量小,定义Q值

(2)
并将增加的1席分给Q值较大的一方。式(2)可以推广到有m方分配席位的情况,当总席位增加1席时,计算Q值为

(3)
并将增加的1个席位分配给Q值最大的一方,这就是席位分配问题的Q值法[3]。
利用Q值法对甲乙丙三系分配21个席位问题的分配结果是:甲系11席,乙系6席,丙系4席。
Q值法的优点是:在pi/ni(i=1,2,…,m)不相等的情况下尽量将相对不公平度降到最低,并且保证了总席位增加时各方所占席位不会减少。然而其缺陷也比较明显,只有当ni≥1时,Qi才有意义,因而Q值法要求各方至少已有一个席位,在总席位比较少或各方人数相差较大的时候可能会导致较大的不公平。
1.3 新Q值法
在新Q值法中,将
(4)
定义为第i方的相对不公平值,称
(5)
为第i方的Q值,并在此基础上提出了新Q值法:先给各方按人数比例取整分配,然后由式(5)计算各方的Q值,再将剩余席位逐一增加给那些Q值较大的各方。

2Q值法的改进探讨
2.1 Q值计算的改进
寻求公平分配席位方法的关键,是建立衡量不公平程度的既合理又简明的数量指标。现借鉴Q值法和新Q值法的思想,从另一个角度对相对不公平度进行定义。
定义:设A、B两方人数分别为p1和p2,所占席位分别为n1和n2,记P=p1+p2,N=n1+n2
当n1/p1 (6) 为对A方的相对不公平度。 当n1/p1>n2/p2时,称 (7) 为对B方的相对不公平度。 以下利用新定义的相对不公平度讨论当总席位增加1席时,应该分配给A方还是B方。假设n1/p1 1)若(n1+1)/p1≤n2/p2,则显然增加的1席应分给A方; 2)若(n1+1)/p1>n2/p2,则说明当A方增加1席时将对B方不公平,此时 (8) 3)若n1/p1<(n2+1)/p2,则说明当B方增加1席时将对A方不公平,此时 (9) 因为公平分配的原则是使相对不公平度尽可能小,所以如 rA(n1,n2+1)>rB(n1+1,n2) (10) 则这一席应分给A方;反之则分给B方。根据式(7)~(9),可知式(10)等价于 (11) 该方法可以推广到有m方分配席位的情况,当总席位增加1席时,计算Q值如下: (12) 可将增加的1个席位分配给Q值最大的一方。为方便起见,不妨将式(12)定义的Q值称为修正Q值。 现用修正Q值讨论甲乙丙三系分配21个席位的问题。 对于前19个席位,采用修正Q值进行分配与采用按比例取整分配的结果是一致的,即甲系10席,乙系6席,丙系3席。 最终的分配结果是:甲系11席,乙系6席,丙系4席,总席位得到了相对公平的分配。这个结果与采用经典Q值法的结果一致,而与新Q值法的结果存在差异。 为便于比较分析,对3种Q值计算公式进行变形后分别为: 3结语 公平的席位分配是一个实用性很强且比较复杂的问题。本研究在Q值法和新Q值法的基础上,对席位分配进行了探讨,给出了相对不公平度的新定义,并在此基础上提出了较为简便的计算Q值的方法,最后对3种方法进行了比较分析。总体而言,修正Q值具有较为直观的意义,且计算简便,适用性强,在席位分配问题中具有一定的实用价值。 参考文献: [1]王若鹏.席位公平分配问题Q值法的改进[J].北京石油化工学院学报,2011,19(2):61-64. [2]邵正隆,王悫,邹向荣.基于Q值法的奖学金自动分配方案的设计与应用[J].计算机应用,2011,31(11):3132-3134. [3]姜启源,谢金星,叶俊.数学模型[M].3版.北京:高等教育出版社,2003. [4]岳林.关于Q值法的一种新定义[J].系统工程,1995,13(4):70-72. [5]高尚.席位分配的最大熵法[J].数学的实践与认识,1996(2):73-75. Improvement of Q-value method WANG Ying (College of Mathematics, Physics and Information Engineering, Anhui Science and Technology University, Chuzhou 233100, China) Abstract:Q-value method is a simple and practical method for processing the fair allocation of seats. After analyzing the advantages and disadvantages of Q-value method and new Q-value method, and refering their ideas to discuss just allocation of seats number, we put forward a new definition of relative unjustice value and a simple calculating method ofQvalue. We also compare and analyze the three methods, reveal the connection and distinction among them. The new method avoids some shortcomings of Q-value method now, which is more reasonable. Key words:relative unjustice value; Q-value method; just allocation of seats number 中图分类号:O221 文献标志码:A 文章编号:1671-8798(2015)01-0011-04 作者简介:王颖(1975—),女,江苏省徐州人,副教授,硕士,主要从事泛函微分方程及高等教育与教学的研究。 基金项目:安徽省重大教学改革研究项目(2014zdjy098);安徽科技学院自然科学研究项目(ZRC2014441) 收稿日期:2014-12-02 doi:10.3969/j.issn.1671-8798.2015.01.003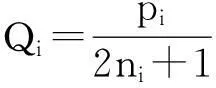
2.2 经典Q值、新Q值与修正Q值的比较