氯离子侵蚀下预应力混凝土桥梁抗弯承载寿命函数

卫 璞，肖汝诚

(同济大学土木工程学院，上海 200092)

混凝土结构在其寿命期内面临诸多耐久性问题，其中钢筋锈蚀最为普遍［1］.主要包括混凝土碳化和氯离子侵蚀，后者不仅产生去钝效应，还会产生去极化作用和导电作用，且氯离子在这一过程中并不消耗，对钢筋锈蚀产生反复催化，造成的耐久性问题往往更为突出［2］.钢筋锈蚀形态分为均匀锈蚀与局部锈蚀，由于组成预应力筋的钢丝尺寸较小，局部锈蚀下，其截面损失远大于普通钢筋混凝土结构，承载能力下降较快［3］，带来严重的耐久性隐患.氯离子侵蚀下的结构耐久性问题越来越得到国内外研究者关注［4-8］.合理描述结构性能退化是耐久性研究的起点，用以描述退化的指标包括状况指标、安全指标和可靠度指标等.近年来，国内外研究者开始使用寿命函数作为结构性能退化指标，如被用于结构维修加固决策［9］和斜拉索换索策略研究［10］等.通过时变可靠度理论结合配分布曲线法［11］可拟合结构的寿命函数，由于分析中可采用目标桥梁处的实测数据，因而能很好地反映目标结构的真实情况.本研究以一座预应力混凝土桥梁为例，分析其在氯离子侵蚀下的预应力筋面积损失，运用蒙特卡罗方法对其抗弯承载可靠性进行研究，拟合其寿命函数，并进行参数分析，为桥梁结构耐久性能研究提供理论借鉴.

1 背景桥梁及其功能函数

1.1 桥梁简介

选用一座跨径为20 m的预应力混凝土T梁作为分析对象，其立面布置如图1所示.桥面总宽11.25 m，由5片T梁构成，梁高1.5 m，跨中截面尺寸如图2所示.桥梁承担公路I级汽车荷载，两车道.主梁采用C50混凝土，预应力筋为Φs15.2 mm高强度低松弛预应力钢绞线，铺装层由80 mm现浇C50混凝土、防水层和100 mm沥青混凝土组成.边梁受力相对不利，将之作为耐久性分析对象，其内设置3束预应力钢束，其中N1钢束由7根钢绞线组成，N2和N3各6根.

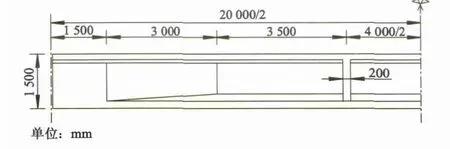
图1 桥梁立面布置图

图2 跨中截面尺寸

1.2 功能函数

桥梁结构在其寿命期内需要同时具备安全性和适用性，我国现行规范对预应力混凝土桥梁的性能要求包括正截面抗弯、斜截面抗剪、抗裂、挠度及使用阶段应力验算等多项内容，这些内容意味着不同的功能函数.完整的结构性能退化分析应当包括结构所需满足的全部功能，研究对应可靠概率的退化情况.本研究仅考虑主梁跨中正截面抗弯承载能力，对应功能函数为

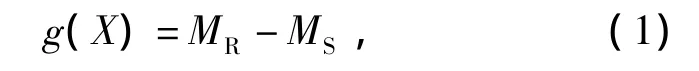
式中:MR为截面的弯矩抗力;MS为截面的弯矩效应.考虑恒载效应MG、汽车活荷载效应MQ及冲击系数Cimp，其表达式为

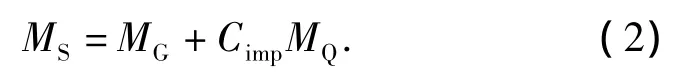
根据公路钢筋混凝土及预应力混凝土桥涵设计规范计算MR，且不考虑普通钢筋的贡献.

2 荷载效应与抗力时变模型

2.1 汽车荷载效应时变模型

汽车荷载效应可按极值分布模拟［12］，100年设计基准期内，其累积分布函数为

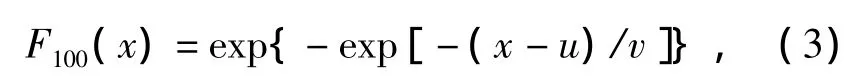
式中:u=0.768 5SQK;v=0.053 7SQK;SQK为按照规范荷载标准值计算的结构效应［13］.则t时间内汽车荷载效应分布函数为

2.2 抗力时变模型

2.2.1 氯离子扩散

氯离子混凝土结构中的扩散过程通常采用菲克第二定律进行描述:

其解为

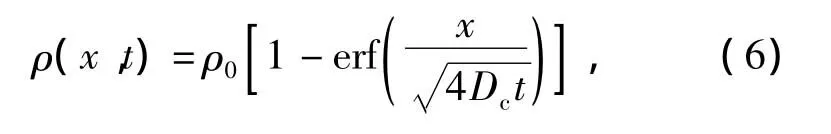
式中:ρ为氯离子质量浓度;ρ0为混凝土表面氯离子质量浓度;Dc为表观氯离子扩散系数;x为计算位置到混凝土表面的距离;t为计算时间;erf(·)为标准高斯误差函数.

当钢筋表面氯离子质量浓度达到临界值ρth时，钝化膜遭到破坏，预应力筋锈蚀开始发生.由上式可得开始锈蚀时间ti:

式中:dp为预应力筋净保护层厚度;erfc(·)为互补标准高斯误差函数.

2.2.2 预应力筋面积的减小

文献［8］通过试验，认为预应力筋局部锈蚀深度可用极值I形分布描述，锈蚀深度概率密度函数为

式中:

式中:a为锈蚀深度(见图3);λ为与参考时间相比，锈蚀物的比率;α，μ 为极值分布参数;α0，e，μ0，e为试验数据获取的极值分布参数;D0为预应力钢丝的初始直径;ic，i为初始腐蚀电流密度;ti为腐蚀开始时间;t0，t0，e分别为实际腐蚀时间参考点、加速腐蚀试验时间;L，L0，e分别为实际预应力钢丝长度、试验钢丝长度;ic，e为试验腐蚀电流密度;κ，θ皆为经验系数，其中，减速腐蚀情况取 κ=0.85，θ=-0.29，匀速腐蚀情况取κ=1，θ=0，此处按匀速腐蚀考虑.

假设锈蚀形成圆形蚀坑［14］，钢丝剩余面积按图3所示几何关系计算，具体算式参考文献［14］.

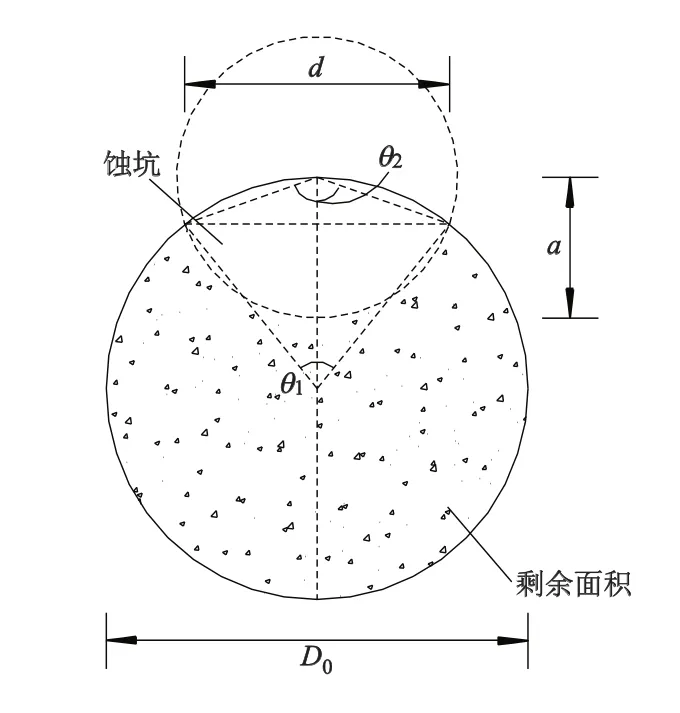
图3 蚀坑形状示意图

由于施工误差等原因，预应力筋保护层厚度存在一定离散性，此外一维氯离子扩散方程也与实际存在差异.为此，偏安全地假定钢束最外侧处氯离子质量浓度达到临界值时，钢束内钢绞线全部开始腐蚀，并且钢绞线外围钢丝发生局部锈蚀，蚀坑深度彼此独立，中间钢丝不锈蚀.

3 蒙特卡罗法计算流程

氯离子侵蚀下的结构可靠度分析随机变量众多，与功能函数间的关系复杂.蒙特卡罗方法采用随机抽样数据进行计算，只需要建立各个变量与功能函数之间的函数传递关系，便能够通过多次模拟得到结构的时变可靠概率或失效概率.

蒙特卡罗法采用随机抽样数据进行计算，只需建立各变量与功能函数间的函数传递关系，便可得到功能函数一系列样本值，进而计算其中安全样本点或失效样本点占总样本点数的比率，进而得到结构的时变可靠概率或失效概率.蒙特卡罗法计算过程方便直接，在结构可靠度分析中得到广泛应用.

采用蒙特卡罗方法计算结构时变可靠概率流程如图4所示.计算所需变量取值如表1(随机变量)和表2(非随机变量)所示，数据来源同时列于表中.其中，氯离子质量浓度等环境参数为相关文献对除冰盐环境的统计值.

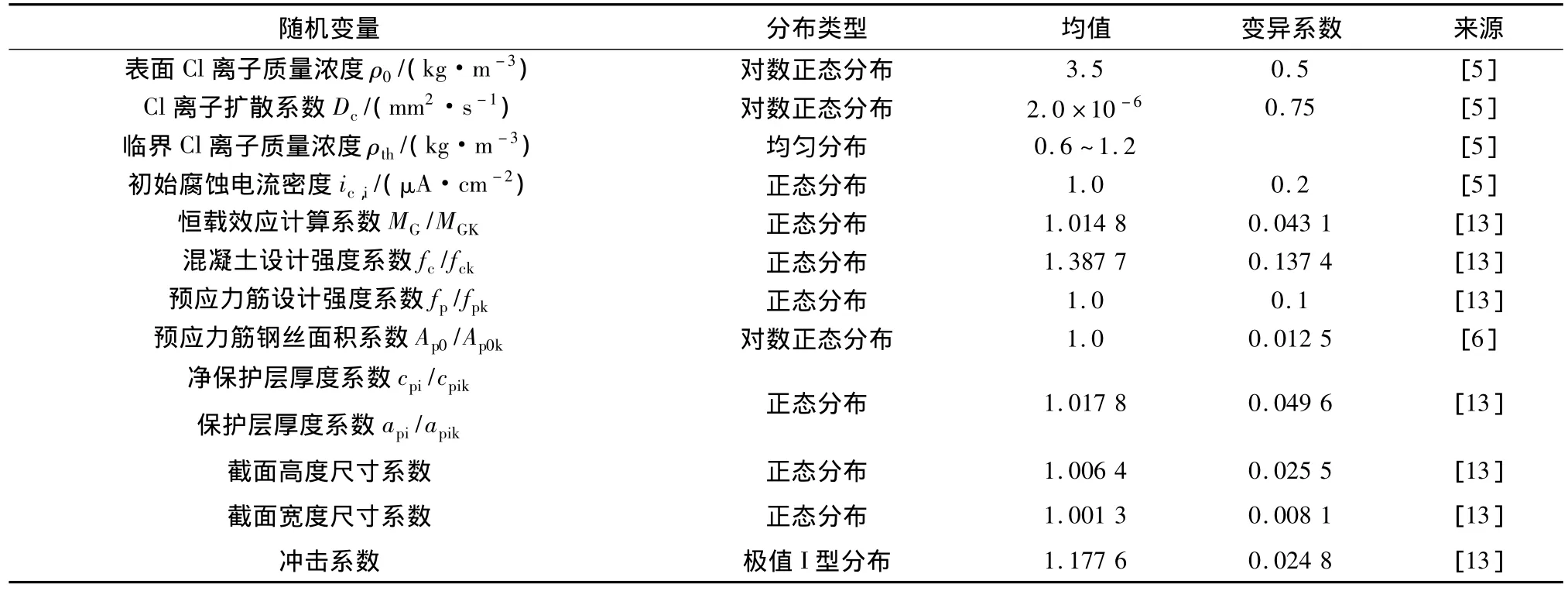
表1 随机变量

图4 蒙特卡罗法计算流程

表2 非随机变量

4 结果及分析

4.1 预应力筋锈蚀分析结果

图5，6分别为N1，N2号预应力筋开始锈蚀时间的模拟计算结果.由于N1号预应力筋侧边保护层厚度(90 mm)小于底边保护层厚度(115 mm)，因此其开始锈蚀时间由侧边氯离子侵蚀控制.N3预应力筋的起锈时间分布应与N1相同，但由于蒙特卡罗模拟计算的不确定性，二者计算结果略有差异，均值均为30.96 a，变异系数则分别为1.707和1.711.

图5 N1钢束开始锈蚀时间概率密度

图6 N2钢束开始锈蚀时间概率密度

由图6可知，N2起锈时间由底边保护层厚度控制，均值为62.29 a，变异系数为1.147.可见，较大的预应力筋保护层厚度可以有效地延长开始侵蚀时间.此外，氯离子的侵蚀可能由预应力筋的任一表面开始，设计时应当保证四周均有足够的保护层厚度.图5，6中实线是用对数正态分布对模拟数据的拟合，可见二者拟合程度较好.因此可用对数正态分布描述氯离子侵蚀下的预应力筋开始锈蚀时间.

图7为预应力筋总面积在不同年份的概率密度函数模拟结果.由图7可知，整个寿命期内，预应力筋面积逐步减小，80 a时剩余面积均值仅为20 a时的1/2左右.此外，面积分布的离散性也在逐步增加.

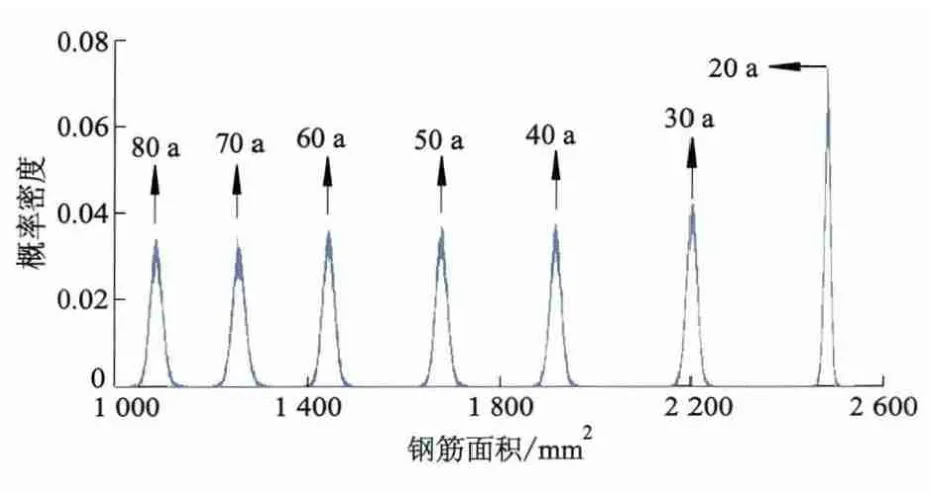
图7 不同年份预应力筋总面积概率密度

4.2 荷载效应及抗力计算结果

图8，9分别为结构跨中弯矩效应和抗力的均值及标准差变化规律.其中荷载效应的时变性由汽车荷载引起，由于其极值分布特性，总效应均值在前十几年内增长较快，此后增长速率相对比较缓慢.

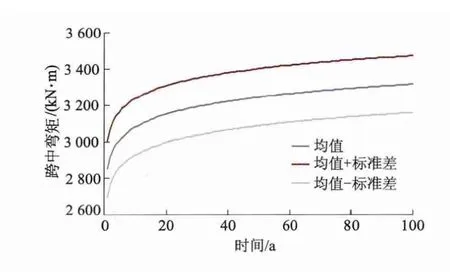
图8 跨中截面弯矩效应

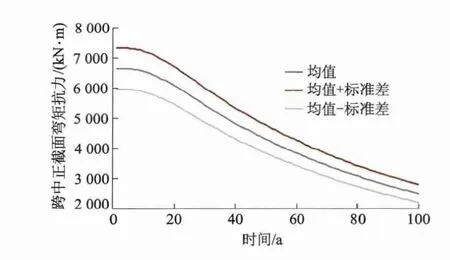
图9 跨中正截面弯矩抗力

抗力均值在其寿命期内逐步减小，末期抗力仅为初期的1/3左右，同时其标准差显示出逐步减小的趋势，这是由于抗力下降速度较快，即使离散性有所增加，标准差的绝对数值仍有可能减小.

图10为抗力变异系数的变化规律.系数在寿命期内逐步增加，反映了对抗力预测的不确定性随时间的增长情况.

图10 跨中正截面弯矩抗力变异系数

4.3 可靠性分析结果

威布尔函数随其参数变化可以灵活地表示不同类型的失效规律，因而得到了广泛应用［9-10］.其可靠概率函数为

式中PS为可靠概率.变形后可得

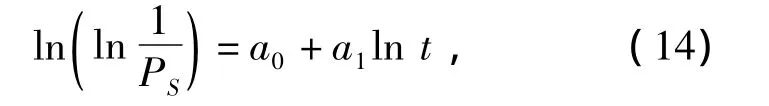
式中:a0=γln λ;a1=γ.通过计算得到的PS-t值进行线性回归，得到威布尔分布参数κ和λ.图11为结构寿命期的正截面抗弯可靠概率及对应的威布尔分布拟合曲线.

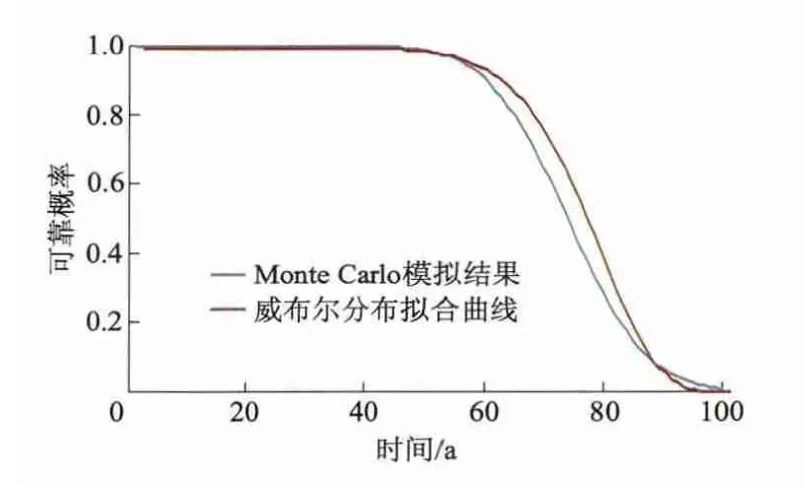
图11 结构寿命期正截面抗弯可靠概率

由图11可知，模拟计算结果与威布尔函数曲线具有很好的相合程度，因此，可以用威布尔型寿命函数作为结构的可靠性描述，并由时变可靠概率的计算结果对其参数进行估计.

5 参数分析

图12，13为主梁梁高和保护层厚度对结构寿命函数的影响.由图12，13可知，主梁梁高变化对结构退化的影响程度较小，这主要由于梁高增加的同时会增加恒载弯矩，同时结构抗力的退化速度较快，初始抗力的提高并不能充分补充后期抗力的衰减.此外，增加梁高会大幅度增加材料用量，经济性能较差.可见，单纯地依靠扩大结构尺寸来应对耐久性问题是不可取的.相比而言，增加保护层厚度并不会带来过大的材料增量，但可以有效地阻止氯离子在混凝土内的扩散，从而延缓预应力筋起锈时间，对耐久性能有较大提高.

图12 主梁梁高对结构退化的影响

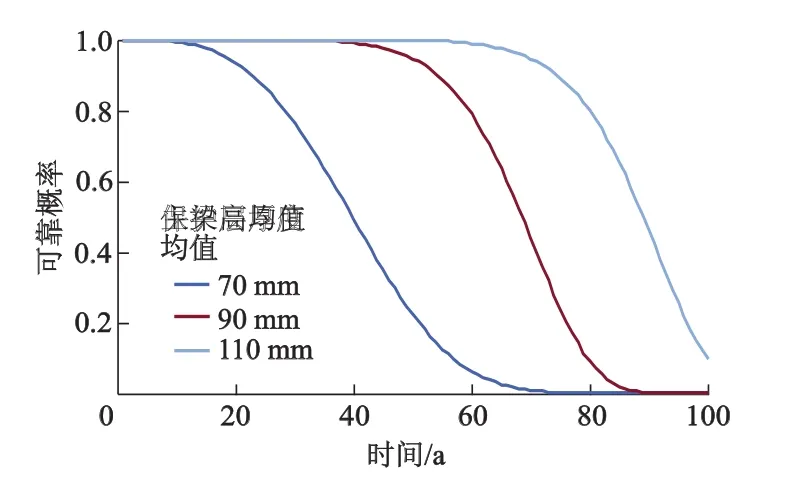
图13 保护层厚度对结构退化的影响

图14，15为结构表面氯离子质量浓度和扩散系数对结构寿命函数的影响，二者对结构耐久性能影响较大.因此，为缓解氯离子环境下混凝土结构的腐蚀问题，应当减小环境氯离子质量浓度，如避免使用含氯离子的混凝土掺合料，减小道路桥梁除冰盐的使用等;或降低氯离子在混凝土中的渗透扩散能力，如使用海工混凝土、混凝土表面涂层、适当增加混凝土保护层厚度等.对于已经进入混凝土内的氯离子应当阻断其与钢筋的接触，如使用环氧涂层钢筋、阻锈剂等，或采用电化学脱盐方法减小混凝土中氯离子质量浓度，并重建碱性环境，使钢筋恢复钝化［2］.

图16为腐蚀电流密度对结构寿命函数的影响.可以看出，减小腐蚀电流密度可以有效地减缓结构退化速率.大部分环境条件下，预应力筋开始锈蚀后，反应速率主要由氧气的供应情况控制［15］，提高混凝土密实度和增加保护层厚度等均能阻断氧气供应，从而减小腐蚀电流密度.

图14 表面氯离子质量浓度对结构退化的影响

图15 氯离子扩散系数对结构退化的影响

图16 腐蚀电流密度对结构退化的影响

6 结论

1)可用威布尔分布描述结构抗弯承载寿命函数，其分布参数由时变可靠概率计算结果拟合而得.

2)单纯采用增加结构尺寸的方法应对耐久性问题效果不佳，且经济性能较差.

3)保护层厚度对寿命函数影响较大，是重要的耐久性设计参数.

4)对于氯盐环境下的混凝土结构，应当针对氯离子质量浓度、扩散系数和腐蚀电流密度等因素采取相关措施.

References)

［1］牛荻涛.混凝土结构耐久性与寿命预测［M］.北京:科学出版社，2000.

［2］金伟良.腐蚀混凝土结构学［M］.北京:科学出版社，2011.

［3］Darmawan M S，Stewart M G.Effect of pitting corrosion on capacity of prestressing wires［J］.Magazine of Concrete Research，2007，59(2):131-140.

［4］Coronelli D，Castel A，Vu N A，et al.Corroded post-tensioned beams with bonded tendons and wire failure［J］.Engineering Structures，2009，31(8):1687-1697.

［5］Stewart M G，Rosowsky D V.Time-dependent reliability of deteriorating reinforced concrete bridge decks［J］.Structural Safety，1998，20(1):91-109.

［6］Akgül F，Frangopol D M.Lifetime performance analysis of existing prestressed concrete bridge superstructures［J］.Journal of Structural Engineering，2004，130:1889-1903.

［7］刘荣桂，陆春华.海工预应力混凝土氯离子侵蚀模型及耐久性［J］.江苏大学学报:自然科学版，2006，26(6):525-528.

Liu Ronggui，Lu Chunhua.Modeling of chloride ingress and durability of maritime prestressed concrete［J］.Journal of Jiangsu University:Natural Science Edition，2006，26(6):525-528.(in Chinese)

［8］Darmawan M S，Stewart M G.Spatial time-dependent reliability analysis of corroding pretensioned prestressed concrete bridge girders［J］.Structural Safety，2007，29(1):16-31.

［9］Van Noortwijk J M，Klatter H E.The use of lifetime distributions in bridge maintenance and replacement modeling［J］.Computers＆Structures，2004，82(13):1091-1099.

［10］王立彬，李爱群，马小利，等.基于寿命函数的斜拉索系统维修更换策略研究［J］.土木工程学报，2012，45(6):162-170.

Wang Libin，Li Aiqun，Ma Xiaoli，et al.Stay-cable maintenance and replacement strategy based on lifetime functions［J］.China Civil Engineering Journal，2012，45(6):162-170.(in Chinese)

［11］张志华.可靠性理论及工程应用［M］.北京:科学出版社，2012.

［12］张建仁，王 磊，薛 雷.考虑抗力劣化的既有钢筋混凝土桥梁车辆荷载取值研究［C］∥中国公路学会桥梁和结构工程分会2005年全国桥梁学术会议论文集.杭州:人民交通出版社，2005:859-864.

［13］GB/T 50283—1999.公路工程结构可靠度设计统一标准［S］.

［14］Val D V，Melchers R E.Reliability of deteriorating RC slab bridges［J］.Journal of Structural Engineering，1997，123(12):1638-1644.

［15］Vu K，Stewart M G.Structural reliability of concrete bridges including improved chloride-induced corrosion models［J］.Structural Safety，2000，22(4):313-333.