无轴承无刷直流电机悬浮力新型控制策略

朱熀秋，单 龙

(江苏大学电气信息工程学院，江苏镇江 212013)

凭借调速性能优良、可靠性高、寿命长、噪声低等优点以及高性能钕铁硼永磁材料的出现，无刷直流电机已在家电、硬盘、CD/VCD等领域得到了广泛的应用［1-3］.由于机械轴承的存在，无刷直流电机在一些免维护、长周期，尤其是在高强度及高转速的场合中已不能满足其要求.无轴承电机具有无接触、无磨损、无需润滑和密封、高速度、高精度、寿命长等优点，在生命科学、半导体工业、食品化工、飞轮储能等特殊传动领域有重要的使用价值和应用前景［4-5］.

无轴承无刷直流电机除了具有一般无轴承电机的优点外，还具备无刷直流电机的无需励磁、高效可靠、出力大等优点，在血液泵、高速/超高速离心机、手术切割电锯等生物医学领域及飞轮储能等新能源领域具有较高的研究价值和广泛的应用前景，因而研究无轴承无刷直流电机具有科研价值和工程意义［6-9］.但在传统无轴承无刷直流电机悬浮力控制方法中，根据检测到转子位置角的不同，选择性的导通悬浮力单相绕组，转子受到的单位电流径向悬浮力较小［10］.电机转子每旋转一周，控制悬浮力绕组的逆变器需通断24次，提高了对逆变器的要求，增加了控制系统的复杂度［11］.逆变器开关频率高，开关损耗大，上述这些问题限制了它的应用与发展.

文中在阐述无轴承无刷直流电机结构及原理的基础之上提出一种悬浮力新型控制策略，并借助Ansoft软件及Matlab/Simulink验证该新型控制策略的正确性.

1 无轴承无刷直流电机悬浮力产生原理

无轴承无刷直流电机结构图如图1所示.

图1 无轴承无刷直流电机结构图

12个定子齿均匀分布于定子磁轭的内圆周表面上，8块永磁体以表贴式均匀分布在转子铁心表面，转矩绕组和悬浮力绕组均采用集中绕组的方式缠绕在定子齿上.其中转矩绕组由A，B，C共3相构成，A1，A2，A3，A4绕组串联连接构成转矩绕组 A相;B1，B2，B3，B4绕组串联连接构成转矩绕组 B相;C1，C2，C3，C4绕组串联连接构成转矩绕组 C相，转矩绕组线圈按 A1，B1，C1，A2，B2，C2，A3，B3，C3，A4，B4，C4顺序沿逆时针方向依次缠绕于定子齿上，电磁转矩产生原理与传统的无刷直流电机相似.悬浮力绕组 SU1，SU2，SV1，SV2，SW1，SW2 等 6个绕组叠压在定子齿内，绕组SU1，SU2为U相悬浮力绕组;绕组 SV1，SV2为 V相悬浮力绕组;绕组SW1，SW2为W相悬浮力绕组，每对绕组串联连接，沿定子圆心对称分布于定子齿上.悬浮力绕组导通时产生的磁通和永磁体磁通相互叠加，打破转子两侧原有的气隙磁密平衡而产生转子径向悬浮力.

图2给出了3相12槽8极无轴承无刷直流电机悬浮力产生原理图.

图2 浮力产生原理图

如图2所示，当转子角θ为0°时，V相悬浮力绕组导通控制转子悬浮，当悬浮力绕组SV1，SV2通以图示方向的电流时，气隙1处的磁密增加，气隙2处的磁密减少，导致转子两侧的气隙磁密不平衡，产生V1负方向的悬浮力FV1，同理，气隙3处的磁密增加，气隙4处的磁密减少，产生V2负方向的悬浮力FV2，因此调节悬浮力绕组SV1，SV2电流的幅值和方向可以产生x轴向的悬浮力Fx，其为FV1和FV2的合力.同理分析可得当U或W相的悬浮力绕组SU1，SU2或SW1，SW2导通时，产生相应的悬浮力，悬浮力绕组的导通情况主要取决于转子角θ，其悬浮力产生的相位如图3所示.

图3 浮力产生的相位

当转子角 θ位于 0°到 15°，45°到 60°之间时，V相悬浮力绕组SV1，SV2导通;转子角θ位于15°到30°，60°到75°之间时，U 相悬浮力绕组 SU1，SU2 导通;转子角 θ位于 30°到 45°，75°到 90°之间时，W相悬浮力绕组SW1，SW2导通.悬浮力绕组以90°为周期轮流导通来产生转子径向悬浮力，使得转子稳定悬浮而无任何机械接触.

在此绕组结构的无轴承无刷直流电机中，采用悬浮力绕组单相导通技术，虽能够使得转子稳定悬浮，但转子受到的径向悬浮力小，这是由于磁通密度分布不平衡的气隙只分布于悬浮力绕组导通的定子齿槽下，而不分布于悬浮力绕组未导通的定子齿槽下.且电机转子每旋转一周，控制悬浮力绕组的逆变器需通断24次，无疑提高了对逆变器的要求，增加控制系统的复杂度.为改变这一现象，文中提出一种悬浮力新型控制方法，采用悬浮力绕组3相同时导通的控制策略来控制转子悬浮.

2 悬浮力新型控制策略

2.1 无轴承无刷直流电机结构

悬浮力新型控制策略的电机结构如图4所示.

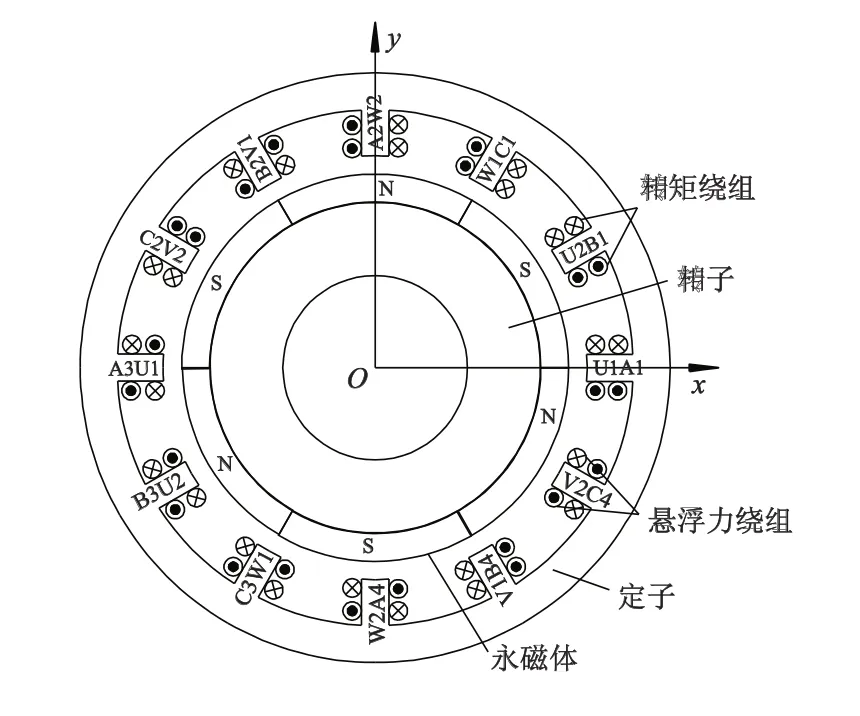
图4 新型电机结构

采用3相12槽6极电机结构，绕组A，B，C为电机转矩绕组，其绕组分布及电磁转矩产生原理与无刷直流电机相似.绕组 U1，V1，W1，U2，V2，W2 分别替代了传统悬浮力绕组 SU1，SU2，SV1，SV2，SW1，SW2，在此电机结构中，悬浮力绕组 U1，V1，W1相在同一时刻导通，悬浮力绕组U2，V2，W2相在同一时刻导通.定义U1，V1，W1相为悬浮力绕组U1-V1-W1，U2，V2，W2 相为悬浮力绕组 U2-V2-W2.每一套悬浮力绕组导通时，转子两侧的气隙磁密分布不平衡，导致在其磁通方向上产生电磁力，3个方向上的电磁力合成矢量使得转子稳定悬浮.

图5为新型控制策略中悬浮力产生原理示意图.

图5 新型控制策略悬浮力产生原理示意图

由图5可见当转子角θ为30°时，悬浮力绕组U1-V1-W1导通，其中悬浮力绕组V1，W1相的电流值大小为悬浮力绕组U1相的一半，且方向相反，以满足3相电流之和为零的要求，转子两侧的气隙磁密分布不平衡导致其受到如图所示的悬浮力FU1，FV1，FW1，因此调节悬浮力绕组 U1，V1，W1 相的电流幅值和方向可以得到x轴向上的径向悬浮力Fx，其为FU1，FV1，FW1这3者的合力.同理，转子径向悬浮力也可以由悬浮力绕组U2-V2-W2导通产生.根据转子角位置的不同，2套悬浮力绕组系轮流交替导通产生径向悬浮力，使得转子稳定悬浮而无任何机械接触.

2.2 悬浮力新型控制策略的实现

在无轴承无刷直流电机的转子径向x轴和y轴向上分别放置2个电涡流位移传感器，利用x轴向上的电涡流位移传感器检测无轴承无刷直流电机转子沿x轴向上的实际位移，将x轴向上给定参考位移x*与实际位移比较之后得到x轴向上位移偏差，差值由PID调节器控制，得到无轴承无刷直流电机转子沿x轴向上的悬浮力给定值，同理，也可以得到沿y轴向上的悬浮力给定值.

图6为两相坐标到三相坐标的2/3变换示意图.

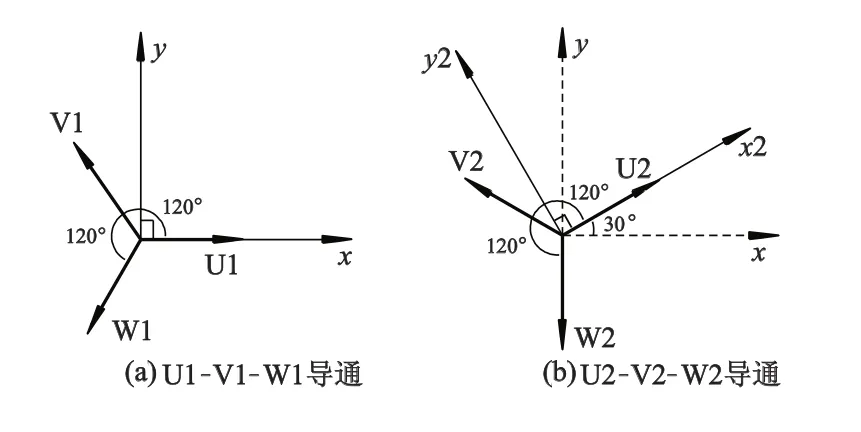
图6 两相到三相坐标系变换

由图6 可见，当转子角 θ位于 15°到 45°，75°到105°之间时，悬浮力绕组U1-V1-W1导通，x，y轴向上的悬浮力给定值，经2/3变换得到 U1，V1，W1方向上的悬浮力给定值，如式(1)所示:

把式(1)代入力电流公式i=KF可得

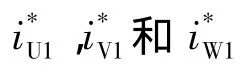
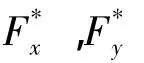
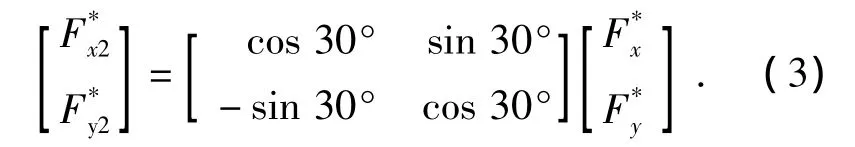
然后x2，y2轴向上悬浮力给定值再经2/3变换后得到U2，V2，W2方向上的悬浮力给定值，如式(4)所示:

把式(4)代入力电流公式i=KF可得

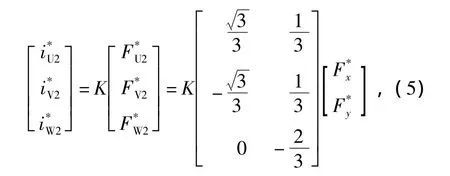
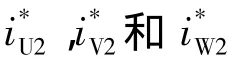
两套悬浮力绕组以120°为周期轮流通电导通，产生径向悬浮力使得转子稳定悬浮，较传统悬浮方法，转子受到的单位电流径向悬浮力将大大增加.且电机转子每旋转一周，控制悬浮力绕组的逆变器仅需通断12次，降低了对逆变器的要求，减小了控制系统的复杂度.

3 有限元分析与仿真试验

3.1 径向悬浮力有限元分析

为了验证悬浮力新型控制策略的有效性，借助Ansoft软件建立无轴承无刷直流电机的二维电磁场模型并对转子径向悬浮力进行验证分析，主要参数为:定子外圆半径40 mm;定子外圆半径15 mm;永磁体厚度2 mm;转轴外圆半径6 mm;平均气隙长度0.5 mm.悬浮力绕组U1-V1-W1导通时的气隙磁密分布云图和磁力线如图7所示.

图7 无轴承无刷直流电机磁密分布和磁力线

由图7可知，悬浮力绕组U1，V1，W1所在的定子齿上的磁通较其他定子齿上的磁通较大，且转子两侧的气隙磁密分布不平衡，转子受到的径向悬浮力合力在x轴向上.

径向悬浮力仿真结果如图8所示.

图8 悬浮力有限元仿真结果

通过对比分析可知，当两种控制方法中的悬浮力绕组通以相同电流时，新型控制策略产生的转子径向悬浮力较传统控制策略提高约为35%.从图8中还可以看出，当悬浮力绕组电流上升到一定值时，转子径向悬浮力将不再增加，径向悬浮力和悬浮力绕组电流不再是理想的线性关系，这是因为在有限元分析计算中，综合考虑了磁路饱和和非线性的影响.这种非线性关系要求在设计无轴承无刷直流电机控制器时，需要考虑磁路饱和和非线性的影响，避免在径向负载较大的情况下，导致悬浮力控制系统失控.

3.2 控制系统仿真试验

运用Matlab/Simulink构建无轴承无刷直流电机控制系统仿真模型进行仿真.起始时间0 s，终止时间0.2 s，仿真选用参数如下:转子转速n=5 000 r·min-1;转矩绕组电阻Rm=1.5 Ω，互感Lm=-0.006 7 H，自感Ls=0.020 H;极对数PM=2;转子转动惯量J=0.005 kg·m2;电机反电动势系数ke=0.382 1;悬浮力绕组电阻Rs=1.5 Ω，自感Ls=0.015 H;极对数PB=1;电机转子质量m=1 kg.

图9为电机转子在x方向未受到干扰力下时的位移曲线.

图9 未受外力时x方向位移曲线

从图9可见，最后转轴仅在中心位置会有微小摆动，基本维持转轴在中心位置小范围内振荡.图10为电机转子在x方向受到40 N干扰力时的位移曲线.

图10 受外力时x方向位移曲线

从图10可见，给x方向一个力的扰动时，系统可以很快地响应并达到稳定状态，转轴振荡后能基本稳定在中心位置.仿真结果证明了该悬浮力控制子系统具有较好动态性能和较快的响应速度.

4 结论

针对传统无轴承无刷直流电机悬浮力控制方法的不足，提出了悬浮力绕组三相同时导通的控制策略，电机转子每旋转一周，控制悬浮力绕组的逆变器仅通断12次，降低了对逆变器的要求，减小了控制系统的复杂度.有限元分析及控制系统仿真试验结果表明，该新型控制策略不仅能够增加转子的单位电流径向悬浮力，而且该控制系统可以实现转子稳定的悬浮，具有良好的动静态性能.

References)

［1］Ooshima M，Takeuchi C.Magnetic suspension performance of a bearingless brushless DC motor for small liquid pumps［J］.IEEE Transactions on Industry Applications，2011，47(1):72-78.

［2］Grabner H，Amrhein W，Silber S，et al.Nonlinear feedback control of a bearingless brushless DC motor［J］.IEEE/ASME Transactions on Mechatronics，2010，15(1):40-47.

［3］朱熀秋，陈雷刚，李亚伟，等.Halbach阵列无轴承永磁电机有限元分析［J］.电机与控制学报，2013，17(4):45-49.

Zhu Huangqiu，Chen Leigang，Li Yawei，et al.Finite element analysis of bearingless permanent magnet motors with Halbach array［J］.Electric Machines and Control，2013，17(4):45-49.(in Chinese)

［4］Sun Xiaodong，Chen Long，Yang Zebin.Overview of bearingless permanent-magnet synchronous motors［J］.IEEE Transactions on Industrial Electronics，2013，60(12):5528-5538.

［5］朱熀秋，王成波，张伟霞.基于电感矩阵的无轴承电机径向悬浮力模型［J］.江苏大学学报:自然科学版，2009，30(1):53-57.

Zhu Huangqiu，Wang Chengbo，Zhang Weixia.Mathematic model of radial suspension force for bearingless motors based on induction matrixes［J］.Journal of Jiangsu University:Natural Science Edition，2009，30(1):53-57.(in Chinese)

［6］朱熀秋，孙晓东，孙玉坤.无轴承永磁同步电机数控系统设计与实现［J］.江苏大学学报:自然科学版，2006，27(6):536-540.

Zhu Huangqiu，Sun Xiaodong，Sun Yukun.Design and realization of digital control system for bearingless permanent magnet-type synchronous motors［J］.Journal of Jiangsu University:Natural Science Edition，2006，27(6):536-540.(in Chinese)

［7］朱熀秋，李元飞.无轴承同步磁阻电机设计及有限元分析［J］.江苏大学学报:自然科学版，2011，32(3):330-335.

Zhu Huangqiu，Li Yuanfei.Design and finite element analysis of bearingless synchronous reuctance motor［J］.Journal of Jiangsu University:Natural Science Edition，2011，32(3):330-335.(in Chinese)

［8］Ooshima M，Miyashita K，Rahman M A.Control circuit topology of a time-divided torque and suspension force control type bearingless motor［C］∥Proceedings of2012IEEE Power and Energy Society General Meeting.San Diego:IEEE Computer Society，2012，doi:10.1109/PESGM.2012.6345015.

［9］Ooshima M，Rahman M A.Control strategy of magnetic suspension and performances of a bearingless BLDC motor［C］∥Proceedings of2011IEEE International Conference on Electric Machines and Drives.Niagara Falls，CA:IEEE Computer Society，2011:71-76.

［10］Ooshima M.Winding arrangement to increase suspension force in bearingless motors with brushless DC structure［C］∥Proceedings of the33rd Annual Conference of IEEE Industrial Electronics Society.Taipei，Taiwan:IEEE Computer Society，2007:181-186.

［11］陈雷刚，朱熀秋.无轴承无刷直流电机径向悬浮力精确数学模型［J］.中国电机工程学报，2012，32(36):75-81.

Chen Leigang，Zhu Huangqiu.An accurate mathematical model of radial suspension force in bearingless brushless DC motors［J］.Proceedings of the CSEE，2012，32(36):75-81.(in Chinese)