基于虚拟迭代技术的汽车喇叭支架疲劳分析

王良模，赵 野，徐 娟，袁刘凯，张汤赟

(1.南京理工大学机械工程学院，江苏南京 210094;2.南京依维柯汽车有限公司，江苏南京 210028)

汽车零部件的疲劳寿命已成为评价汽车产品品质的重要因素之一，零部件的疲劳问题越来越受到各大主机厂的关注.疲劳寿命评估的传统方法是在试验场进行道路试验，这种方法直接准确，但是会消耗大量人力物力［1］.CAE(computer aided engineering)方法的基础是获得车身或零部件连接点处可信的载荷谱或者加速度谱.采用多体动力学仿真提取载荷谱时一般是以编制的路面位移输入［2］，由于输入非真实的道路载荷谱，提取的载荷缺乏可信度，而且轮胎特性的准确模拟一直是个难题［3］，需投入大量资源.利用六分力传感器可以获得较精确的轴头六分力响应信号，但六分力传感器的造价昂贵.如何以低成本获取合理的零部件载荷谱，已成为制约CAE疲劳分析的重要因素.

虚拟迭代技术基于实车道路试验采集容易得到的信号，通过建立多体动力学模型迭代求解，可以得到各连接点的力，再进行疲劳寿命预测和结构优化，满足产品可靠性设计目标［4］，具有成本低、周期短等优点.目前Magna公司正在推广虚拟迭代技术，国内厂商正逐步将此技术应用于汽车产品设计开发上［5-6］.

笔者针对某轻卡喇叭支架的避振片断裂问题，对该避振片进行疲劳分析，重点介绍刚柔耦合多体动力学模型的建立及虚拟迭代载荷提取的过程，在此基础上对喇叭支架进行疲劳分析，分析避振片损伤位置与实际断裂位置吻合情况，验证虚拟迭代技术应用在汽车零部件疲劳分析中的有效性.

1 虚拟迭代原理简介

虚拟迭代的实质是根据已知的响应，迭代出系统的驱动.可以通过试验场实车测试得到相关部件响应信号(悬置下方的测量信号)，通过FEMFATLab进行虚拟迭代反求出所加激励处的外部激励，将反求出的外部激励重新激励系统便可提取出所关心部位的载荷.迭代的整个过程:创建白噪声，获得响应，求取传递函数，加载期望信号求解初始驱动，获得虚拟迭代响应信号，响应信号与期望信号对比，重复迭代.文献［7］对此作了比较详尽的阐述.

驱动可以是外力或者绝对位移，响应可以是加速度、应变、相对位移或者系统内力.利用白噪声激励系统，获得相应响应，得到系统的传递函数:

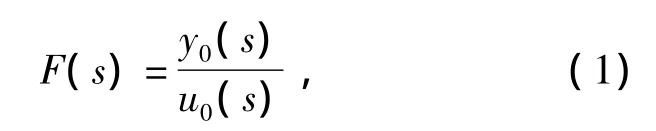
式中:u0(s)为系统输入;y0(s)为相应的系统响应.

从而可得F-1(s)，根据试验得到的期望信号yDesired(s)可以获得初始驱动信号:

用初始驱动信号激励系统，可以获得相应的响应y1(s).因Adams中建立的样机模型是个非线性系统，而传递函数是线性的，所以y1(s)与yDesired(s)会有一定的误差，需要反复修正驱动信号(激励)，使响应信号逼近实测值，最终得到近似等效的激励输入.

用F-1(s)继续作用于响应误差(yDesired(s)-y1(s))，用修正参数a加以修正并与初始驱动叠加，以此类推，第n次的迭代可表示为

信号比较包含时域曲线比较、功率谱曲线比较和相对损伤值比较等.时域曲线主要比较相位幅值和趋势吻合度;功率谱曲线比较幅值和趋势吻合度;相对损伤值接近1.0.

2 虚拟迭代过程

2.1 多体动力学模型建立

多体动力学模型的精度是影响迭代结果的重要因素，而刚柔耦合多体动力学已经成为车辆系统动力学发展的一个趋势［8］.车架的运动形式是否正确将会直接影响迭代结果，为了提高迭代的准确性，采用柔性体建模方法建立车架以及驾驶室的多体动力学模型;同时建立模型过程中对结构进行简化，这一简化要以符合结构主要的力学特性为前提.由于后半部分车架与驾驶室并非直接相连，驾驶室运动的主要直接输入点在前半部分车架，采用半车架模型进行迭代.

喇叭的质量约为1 kg，质量相对较轻，对迭代结果影响较小.模型中对喇叭总成进行柔性化，图1a为喇叭支架前4阶模态振型，分别为避振片1阶弯曲(41.4 Hz)、避振片1阶扭转(57.7 Hz)、避振片2阶弯曲(111.3 Hz)和避振片2阶扭转(152.4 Hz)，采用固定副连接模拟喇叭支架的螺栓连接.驾驶室形状复杂，有很多钣金件，各零件之间通过焊接、铆接等方式进行连接［9］，利用Hypermesh进行网格划分处理.驾驶室中性文件中包含有很多局部模态，图1b为整个驾驶室参与变形的前4阶模态振型，性质分别为左门参与较多的驾驶室弯曲变形(27.9 Hz)、右门参与较多的弯曲变形(28.7 Hz)、1阶扭转(53.5 Hz)以及驾驶室地板前部弯曲变形(60.1 Hz).取车架的前59阶模态，驾驶室取前46阶模态，模型中乘员采用质量点模拟，以刚性单元连接到相应部位.

图1 支架及驾驶室前4阶整体振型

悬置刚度是影响模型准确度的重要参数，车架与驾驶室之间有6个悬置，悬置的刚度曲线由拉伸、压缩试验获得，通过Gforce函数来模拟衬套的非线性刚度特性.

当所研究的多体动力学模型系统的固有频率分布贴近期望信号的频率分布时迭代过程会更平稳.车架以下部分可视作台架，当迭代发散或者驱动对应的响应出现毛刺时可适当增加台架的质量，提高系统的稳定性，使迭代更加容易进行.

根据车辆7自由度模型的简化思想，对模型的4个激励点的z向(垂直方向)、2个y向(侧向)和1个x向(纵向)施加外部激励约束.模型中下方4个激励点总共限制了4个自由度;车架为柔性体，可视为小变形，侧向及纵向的3个激励约束限制了车架沿x，y向的运动以及绕z向的转动.在6个悬置上、下端以建立加速度响应;在喇叭支架连接点处建立提取载荷所需的力响应.完整的多体动力学模型如图2所示，在6个悬置处分别建立相应的Request，其中左前悬置下端的z向、右前悬置下端的x，y，z向、左后悬置下端的z向和右后悬置下端的y，z向这7个通道为迭代信号通道.多体动力学系统迭代模型总共设有7个外部激励点和13个响应点.

图2 车架与驾驶室多体动力学模型

2.2 数据采集与处理

试验数据曲线由在定远试验场进行的实车路试采集而来.在车架与驾驶室之间的6个悬置点上、下端各布置1个3向加速度传感器，悬置下端传感器采集的信号将作为迭代目标信号(期望信号);悬置上端的测量信号作为监测信号.分别在砂石路、搓板路、鹅卵石路、扭曲路等路面上进行信号采集.最终采集的信号总时长为640 s，如图3所示，对应的总测试路程约为6 km.对采集的信号进行单位转换、将测量信号按256.0 Hz进行重采样、滤波、截取等处理.

图3 7通道期望信号

所研究对象喇叭支架是安装在车架右前端靠近右前悬置处，右前悬置处的信号迭代结果精确与否将显著影响所要提取的载荷谱的准确度.将左前悬置下端的z向、右前悬置下端的x，y，z向、左后悬置下端的z向和右后悬置下端的y，z向加速度信号筛选出来作为迭代目标信号.

2.3 迭代过程及结果评价

基于FEMFAT-Lab相关软件进行迭代.将多体动力学求解文件导入，定义输入、输出通道，输出的7条响应顺序应与期望信号的排列顺序相一致.经过创建白噪声、求取模型传递函数、选择期望信号、产生初始驱动和选择迭代步数等过程，即可进行迭代，初步选择迭代步数为8步.

图4仅显示了右前悬置下端z向信号在初步的8次迭代结束之后的迭代情况，通过与相应的期望信号在时域内对比可见迭代响应信号与期望信号已经比较接近.各路段以及各过渡路段的迭代信号都在逼近期望信号，未有出现发散现象.其他6个通道的迭代效果也很好，将迭代步数增加至15步.

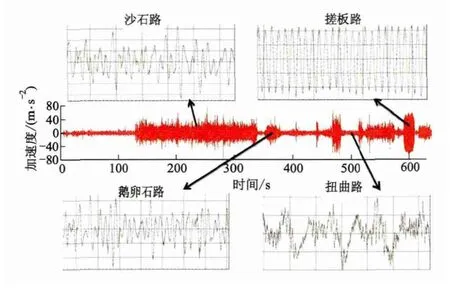
图4 右前悬置下端z向信号第8次迭代结果

迭代结果通常采用的评价方法:通过比较迭代出来的响应信号与试验采集信号的时域曲线图可以直观地看到信号迭代的准确程度，从而直观地评价结果的准确性;相对损伤值分布图从损伤的角度反映了迭代出来的响应曲线是否与期望曲线一致;功率谱密度曲线可以从能量分布的角度比较二者的差异.

以相对损伤值为例评判此次迭代结果的准确性:图5a为迭代过程中各通道响应信号与期望信号之间的相对损伤值变化趋势图，迭代进行了15次，由图5a可见各通道的相对损伤值趋于平稳并且接近数值1.000，说明了迭代结果的可信度很高;图5b是15次迭代结束之后各通道的迭代响应信号与期望信号的相对损伤值，左前z向、右前x，y，z向、左后z向、右后y，z向7个通道的相对损伤值分别为 1.006，1.064，0.999，1.007，1.007，0.987 和1.006.各通道相对损伤都很接近1.000，迭代结果较准确.

时域信号越吻合、相对损伤值越接近1.000，说明响应信号与期望信号越吻合，即相应部位的变形越接近实测情况.本研究的对象喇叭支架是安装在车架右前悬置附近，对应的右前悬置3个方向(x，y，z向)的迭代信号与试验获得的期望信号的相对损伤值分别为1.064，0.999和1.007，迭代结果可以接受.

图5 相对损伤值分布

3 载荷提取与疲劳分析

3.1 载荷提取

进行疲劳寿命分析首先要了解构件的载荷情况，载荷随时间变化的历程称为载荷谱.结构所承受的真实载荷往往是不规则的，在计算时必须对这些不规则载荷进行处理，得到计算载荷谱，而对这类事件的分析普遍应用循环计数法［10］.迭代完成之后，从生成的结果文件中可以直接读取到支架安装点处的载荷.提取喇叭支架连接点处的3个方向的力作为支架疲劳分析所需的载荷谱，如图6所示.对载荷谱进行适当滤波，因低频部分对疲劳计算的影响很小，将0.1 Hz以下的低频信号滤掉.

图6 喇叭支架安装点处提取的载荷

3.2 疲劳损伤机理及累积损伤模型

疲劳失效是荷载反复作用的结果，材料在应力或应变的反复作用下发生了性能变化［11］.工程中常用的疲劳分析方法有3种:名义应力法、局部应力应变法和损伤容限法.通常，疲劳过程可以观察到以下4个阶段:裂纹成核、微观裂纹扩展、宏观裂纹扩展和最终断裂.工程应用中，通常将零件在裂纹成核和微观裂纹扩展期间的寿命长度称为裂纹萌生阶段，而将零件在宏观裂纹扩展期间的寿命长度称为裂纹扩展阶段，对从萌生到扩展的过渡阶段无法做出精确的定义.

利用道林(Dowling)1998年提出的光滑试样线弹性断裂力学可以估算出裂纹萌生尺寸:

式中:ΔSe为疲劳极限应力范围;ΔKth为R=-1时的临界强度因子的范围，R为应力比.

零件的损伤可以用趋向可接受最大裂纹长度的裂纹长度累积量来表示.曼森和哈尔福德(Manson and Halford)在1981年提出了裂纹扩展方程:

式中:n为达到裂纹长度a时外加载荷的循环次数;a0为初始裂纹长度;Nf为在达到最终断裂的裂纹长度af时外加载荷的循环次数;αf为根据经验确定的指数，可根据式(6)进行计算:

累积损伤(D)是瞬时裂纹长度与最终裂纹长度的比值:

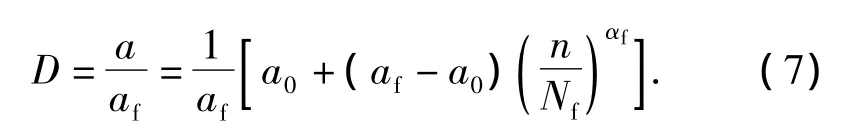
这个损伤公式表示:当疲劳损伤D大于或等于1(即a≥af)时，就会发生疲劳失效.

3.3 疲劳分析及结果对比

运用有限元法进行零部件疲劳分析时主要有模态叠加法和惯性释放法2种.惯性释放法的原理相对简单，没有考虑共振的影响;模态法为任何以振动为主或者动态加载的部件的疲劳寿命分析提供了技术分析手段［12］.如果结构中某部位的载荷可能激发共振模态，那么线性叠加将可能无法准确地计算由此产生的应力时间历程.选择模态叠加法对支架进行疲劳分析，在HyperWorks中对模型进行前处理，获得模态应力和模态坐标作为耐久性分析的输入，采用E-N法计算喇叭支架避振片的疲劳累积损伤，避振片的材料为65Mn.

图7为循环1 400次、对应的道路试验里程约为8 400 km的计算结果，避振片最大损伤值为31.356，远大于1.000，该区域位于避振片上端螺栓孔下方附近位置，将产生疲劳失效，这与喇叭避振片的实际断裂部位一致，验证了虚拟迭代结果的正确性.

图7 计算结果与样品实际断裂位置对比

4 结构改进

根据仿真分析和实际断裂的情况，考虑到避振片属于标准件，单个避振片的结构不可随意改动，因此，通过增加1片避振片来提高支架的使用寿命.用同样的方法对改进后的支架进行疲劳分析，循环1 400次的计算结果显示避振片处最大的损伤值为0.011，循环5 000次的损伤值为0.038，远小于1.000;将改进后的支架安装在整车上，在定远试验场进行疲劳道路试验，结果表明:支架通过了试验，满足疲劳寿命的要求.

5 结论

1)通过建立柔性车架和驾驶室，提高了多体动力学模型的精确度，使得迭代的结果更加可信;基于提取到的载荷谱得到的避振片疲劳分析结果与实际完全吻合，验证了虚拟迭代结果的正确性.

2)研究对象喇叭为典型的汽车挂件之一，使用的方法具备通用性，对于车架上的其他挂件的疲劳载荷提取具有一定的借鉴意义;对于驾驶室疲劳分析所需的载荷可通过提取驾驶室悬置上的力获得.

References)

［1］沈宏杰，周 鋐.汽车零部件道路模拟加载谱研究［J］.汽车工程，2010，32(2):159-162，142.

Shen Hongjie，Zhou Hong.A study on the loading spectra for the road simulation of vehicle components［J］.Automotive Engineering，2010，32(2):159-162，142.(in Chinese)

［2］Cui An，Liu Zihui，Zeng Qingyang，et al.The layout and fatigue life analysis of welding spots for the cab body in white of a commercial vehicle［C］∥Electronic＆Mechanical Engineering and Information Technology.Piscataway，USA:IEEE，2011:2089-2093.

［3］Taheri S，Sandua C，Taheri S，et al.A technical survey on Terramechanics models for tire-terrain interaction used in modeling and simulation of wheeled vehicles［J］.Journal of Terramechanics，2015，57:1-22.

［4］Fischer P，Witteveen W.Intergrated MBS-FE-Durability analysis of truck frame components by modal stresses［C］∥ADAMS User Meeting，2000:1-15.

［5］邵 建，董益亮，肖 攀，等.基于多体模型仿真的载荷谱虚拟迭代技术分析［J］.重庆理工大学学报:自然科学，2010，24(12):84-87.

Shao Jian，Dong Yiliang，Xiao Pan，et al.Virtual iteration technology of load spectrum based oil multiple body simulation［J］.Journal of Chongqing University of Technology:Natural Science，2010，24(12):84-87.(in Chinese)

［6］钱立军，吴道俊，杨年炯，等.基于道路模拟激励的汽车下摆臂多轴疲劳分析［J］.汽车工程，2012，34(3):249-254.

Qian Lijun，Wu Daojun，Yang Nianjiong，et al.Multiaxial fatigue analysis of vehicle lower control arm based on simulated road excitation［J］.Automotive Engineering，2012，34(3):249-254.(in Chinese)

［7］Helmut D，Matthias M，Otmar G，et al.Integrating virtual test methods and physical testing to assure accuracy and to reduce effort and time［C］∥SAE Technical Paper Series.USA:SAE Publication Group，Paper Number:2006-01-3563.

［8］Lu Yaohui，Zeng Jing，Wu Pingbo，et al.Modeling of rigid-flexible coupling system dynamics for railway vehicles with flexible bogie frame［C］∥Fourth International Conference on Innovative Computing，Information and Control，2009:1355-1360.

［9］王良模，陈东益，邹小俊，等.某轻型卡车正面A柱撞击仿真与改进［J］.江苏大学学报:自然科学版，2014，35(2):132-136，143.

Wang Liangmo，Chen Dongyi，Zou Xiaojun，et al.Simulation and improvement of a light truck in A-pillar impact［J］.Journal of Jiangsu University:Natural Science Edition，2014，35(2):132-136，143.(in Chinese)

［10］高东明，王德成，王光辉，等.草地切根机切刀的疲劳寿命分析［J］.江苏大学学报:自然科学版，2012，33(3):283-287.

Gao Dongming，Wang Decheng，Wang Guanghui，et al.Fatigue life analysis of root cutting machine blade［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(3):283-287.(in Chinese)

［11］任伟平，李小珍，李 俊，等.公轨两用钢桁桥轨道横梁与整体节点连接头的疲劳荷载［J］.中国公路学报，2007，20(1):79-84.

Ren Weiping，Li Xiaozhen，Li Jun，et al.Fatigue load of welded connections between rail across beams and integral joints of combined steel truss bridges［J］.China Journal of Highway and Transport，2007，20(1):79-84.(in Chinese)

［12］Gaier C，Dannbauer H.A multiaxial fatigue analysis method for ductile，semi-ductile，and brittle materials［J］.The Arabian Journal for Science and Engineering，2008，33(1):223-235.