一种改进型声线修正算法在超短基线定位系统上的应用

范赞(昆明船舶设备研究试验中心，昆明，650051)



一种改进型声线修正算法在超短基线定位系统上的应用

范赞
(昆明船舶设备研究试验中心，昆明，650051)

摘要根据声线分层恒速修正原理和超短基线设备测量的水下温度、深度信息，结合系统海上使用的环境特性，提出一种改进型声线修正新算法进行水下精确测距。该算法通过湖上试验和海上验证，较传统平均声速算法大幅提高测距精度，有效解决了声线在水下复杂环境中曲线传播的难题，提高了超短基线定位系统的水下测距及定位精度。

关键词超短基线；水声定位；声线修正；应答器；步长

超短基线定位系统由于体积小、重量轻、携带方便等优点，在水下定位领域应用广泛，其定位原理是利用水下应答信号到达接收单元之间的相位差（或时延差）结合水下测量目标到超短基线阵之间的斜距来实现的[1]。超短基线定位系统水声信号在水下传播过程中，随着水温和深度的变化，声线以曲线轨迹方式进行传播，那么从水下测量目标到超短基线阵（基阵孔径很小）上接收单元的声线轨迹的弯曲程度必定非常接近，几乎一致，因此声线弯曲传播对超短基线两个接收单元的相位差（或时延差）值影响非常小，但影响传统水声传播时差测距的精度，与真实值存在较大的偏差，带来系统定位误差。因此运用超短基线定位时需要对水声传播的声线进行修正，提高水声测距和定位精度。

1　声线修正原理

为了精确逼近实际声线轨迹，同时考虑工程应用中数据处理的能力，修正算法拟运用现场测试得到的深度、温度等信息，在垂直剖面上将目标深度进行等高度分层，把复杂的声速垂直分布剖面近似视为由多层恒定声速构成，即用每个分层为同声速层(声速递度为0)的声速分布来代替连续变化的声速分布，然后每一层用一段折线来逼近实际声线轨迹[2]。图1为声速传播轨迹示意图。

假设将水面到水下S目标的垂直深度分N层，每层深度相等，每一层为恒定声速传播，那么声速轨迹为折线，因此可以直接用声线轨迹图来求每一层的水平距离Δxi和Δti，ΔZi为每层深度值，其中Z0= Z1=……Zi，i=(0、1、2、……N)。

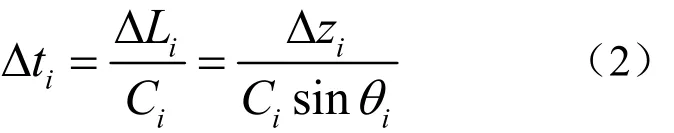
图1　声速传播轨迹示意图

在分层介质中，射线声学遵循Snell 定理[2]

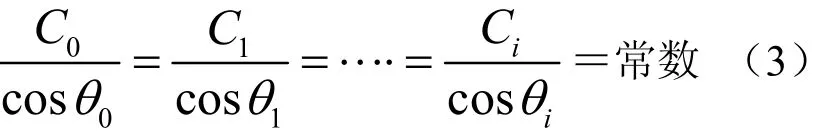
式中： C0和θ0为起始出发层的声速和掠射角，Ci为第i层处的声速，θi为第i层边界处的掠射角。任意复杂的声速垂直分布，可近似划分成每层声速恒定介质的连接，共分成N层，总的声线行程L和声线单程时间t等于N层的ΔL 和Δt的叠加[2]，于是

水声信号从水下目标S处到接收单元O处的传播总时间t，可以通过应答模式或同步模式精确测得，在系统可以测量水下目标深度的情况下，把水下目标S分层到最后一层上，利用公式（3）、（5）来反推θ0的值，在Ci(i=0、1、2……N)数值已知的基础上，θj(j=0、1、2……N)值可以通过公式（3）用θ0与Ci(i=0、1、2……N)来表示，然后代入公式（5），那么整个解算方程就只有一个未知项θ0，由于整个计算复杂，直接计算出θ0相当困难，实际工程应用中可以通过编程运用“夹逼法”得到初始掠射角θ0。

图2　“夹逼法”计算流程图

“夹逼法”计算流程如图2所示，主要步骤如下：

（1）利用深度传感器测得系统接收单元与水下目标的深度差H，将1500 m/s(参考声速)乘以总时间t得到斜距估值，然后利用公式（6）来估算出θ0'，此时θ0'大小很接近0θ。

（2）利用一个非常小的Δθ值，进行(θ0'+Δ θ)或者(θ0'−Δ θ)的运算，将结果代入公式（5），每次算出的时间t'与测得的总时间t相比较，结果需要满足t− t'≤Δ t（其中Δt越小，计算的角度越接近真实值），否则将步骤（2）一直循环进行下去，直到满足要求。

（3）在计算出θ0的数值后，利用公式（3）计算出θj(j=1、2……N)，代入公式（7）来计算出水平总距离X，在得到深度差H和水平距离X后，运用直角三角形公式（8）就可以得到超短基线阵与水下目标较为真实的斜距。

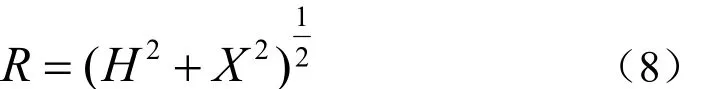
2　算法内容改进及应用

为了现场操作便利，使系统适应性更广，系统通过在超短基线阵和水下应答器上的温度和深度传感器，测量出水下应答目标和超短基线阵两点的周边水温值和深度值，利用水声遥测技术将水下应答器测量的信息发回平台，再结合海洋盐度平均值(S=3.6%)，运用海洋声速公式解算出超短基线阵和水下应答器这两点的声速值[3]。水下应答器的应用水深达不到深海等温层，因此声速剖面分布主要受海水温度影响，参考图3所示的典型浅海温度剖面图，可以认定冬季大多为等温层声速剖面，夏季则为负跃变层声速梯度剖面[3]，而夏季水下40 m深度以内声速梯度变化较大，修正算法以40 m深度为界，大致将水下声速区域划分为阶跃变化和等差变化两大块。

算法参考图3声速变化趋势图，以超短基线阵与水下应答器两处温差T结合水面温度T0为判断条件，当T0>15℃时,声线修正算法为以下两类，如果T0<15℃时，则以第一类算法修正声速：

1、当超短基线阵与应答器两处测量水温差值T不大于5℃时，则认为从超短基线阵到水下应答器之间为等声速梯度(假设声速梯度为g)区域。其中超短基线阵、水下应答器两处分别通过测量温度，计算出声速为C1和C2，

其中n为垂直距离分层的层数，那么根据公式（9），可以得到每层的声速值，再运用声线修正原理计算出精确的R值；

2、当超短基线阵与应答器两处测量水温差值T大于5℃时，以40 m深度为界，大于40 m深度区域声速采用第一类声速方法测距；而在40 m内，从水面而下每相邻层的声速梯度为kig(k>1,i=1、2……m−1)， m(m>3)设定为40 m深度内分层数。根据图3可知k值从水面开始由小变大，在声跃层时达到最大，再每层逐渐衰减。同时随着超短基线阵周边水温值T0越大，初始值k1也越大，每层衰减的比例也增大，根据经验公式：

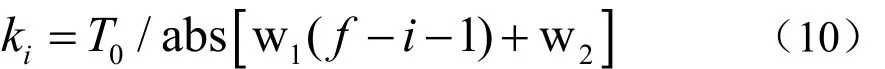
式中：abs为取绝对值符号；w1、w2为固定常数；i=1、2……m−1； f=round(m/2)，round为四舍五入符号。再将ki值代入式(11)计算出g值：

其中n为垂直距离分层的总层数，再根据g、k、C1和C2值计算出每层声速值，最后通过声线修正算法完成R值的解算。

3　算法效果检验

借助国内湖上某水下环境测量系统，在7月利用声速仪和温度传感器在0～50 m深度范围内每5 m测量一次。而在50～100 m深度范围内，每10 m测量一次，获取一组精确数据，假定5 m和100 m声速值为已知，对各类算法效果进行比较和检验，实测与各类算法计算的声速图见图4，具体测量和计算数据见表1。

图4　实测与各类算法声速变化曲线比较图

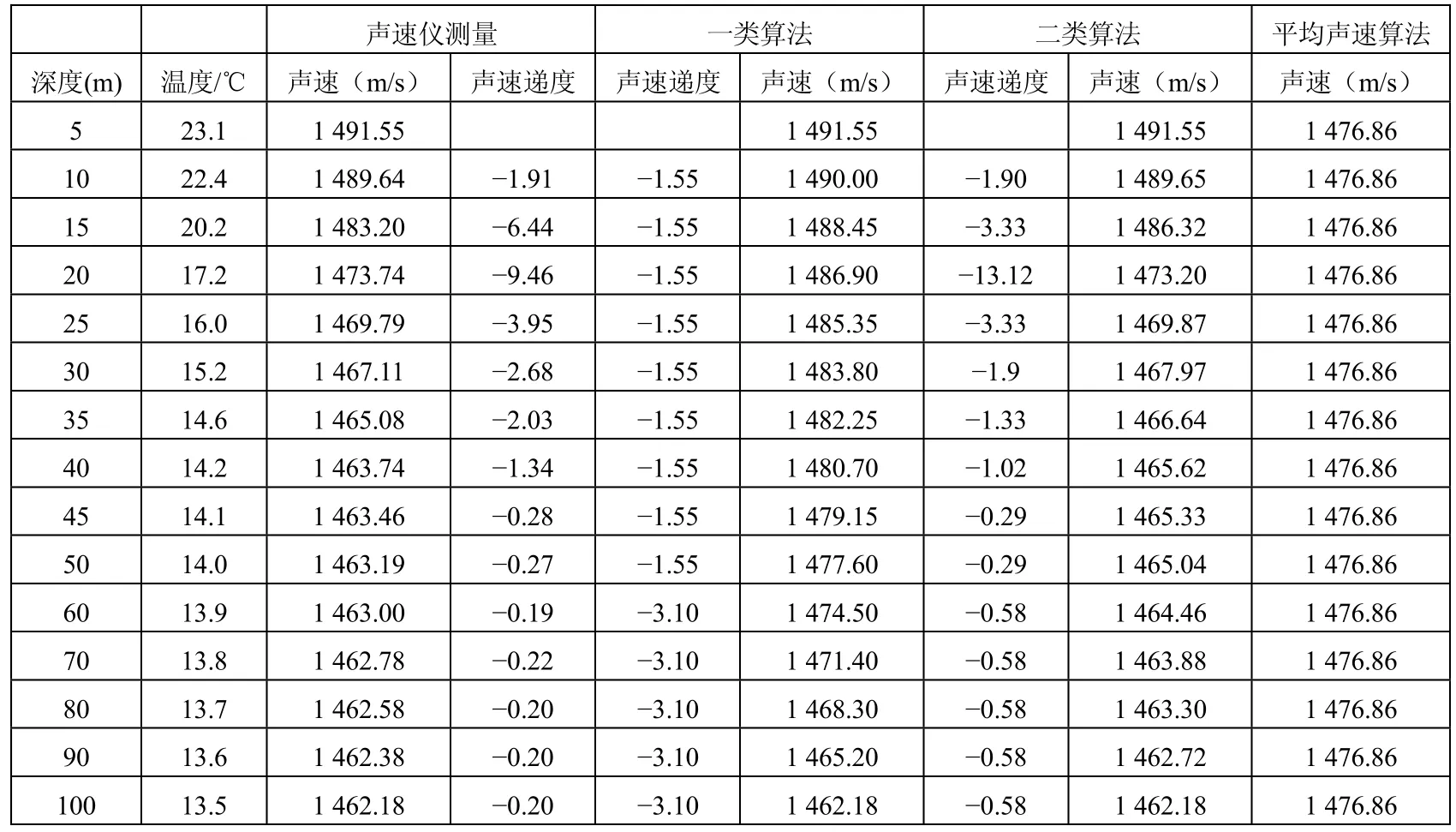
表1　各类算法与实测数据比较

以在夏天我国南海区域进行系统测试为例：超短基线水深5.6 m，温度24℃；应答器水深72.2 m，温度11℃；水声应答信号传播时间为88.3 ms。海水温度24℃和11℃处由式（12）计算分别为1 532.0 m/s和1 494.1 m/s。

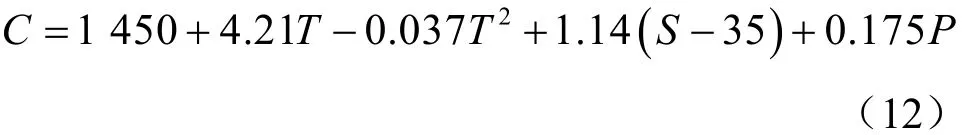
根据传统平均声速定位算法，得到Ra值为133.604 m。而考虑超短基线阵与应答器两处温度差值为12℃且超短基线阵周围水温为24℃，因此采用第二种算法处理，运用声线修正算法将水面到应答器之间的垂直深度分为15层，每层5 m，那么超短基线阵处在第2层，应答器处在最后一层，依据第1、2节算法计算出Rb为135.2892 m。两种方法结果比较，改进型修正算法在测量斜距时比传统测距计算精度高1.26%((Rb−Ra)/Ra)。当分层深度步长设置更小时，层数越多，那么根据改进型修正算法特性，其计算的精度还会更高。

从图4和表1可以明显看出，以7月份湖上声速仪测量数据为真实样本，在100 m深度范围内比较各类算法的声速变化曲线，第二类算法的声速变化曲线与声速仪测量声速曲线最为接近；第一类算法次之；而传统平均声速算法由于只简单平均起始两点声速值，与声速仪测量声速曲线最不符。

同样由海上系统测试结果也可以得出在水温变化较大，特别是在声跃层附近的水深区域，传统的平均声速处理方法不能模拟真实的声速梯度变化，与改进型声线修正算法相比，测距误差较大。但在深度垂直剖面上，如果温度相差不大或者冬季海域，各深度层的声速梯度变化小，依据以上各类算法计算的测距结果差值也不大。依据图4声线变化的趋势，沿深度垂直剖面分析，当水下目标深度延伸到海洋等温层甚至更深，声速梯度逐步由水压值主导，声速梯度变化非常小，随着声跃层在整个深度垂直剖面所占的比重越小，传统平均算法计算与改进型声线修正算法的测距误差将逐步减小，测距结果并也逐渐向真实值靠拢。

4　结束语

随着我国近年海洋工程的迅速发展，超短基线系统使用越来越广泛，国内海上应用的超短基线定位系统几乎全为进口，其产品也属不同技术阶段，在水声修正算法方面也是从无到有。国外最新的第5代超短基线系统，也是在基阵与应答器上配备温度和深度传感器，其水声修正具体技术方法无从得知，但国外公司有海洋水声测量数据库和长期的实践经验，修正效果超过国内水平。在国内已经实现超短基线国产化的基础上，文章根据海上运用经验，提出了一种编写简单实用、计算复杂性低、易于实现和工程实用性强的声线修正算法，较好的解决了声线在水下复杂环境中曲线传播的难题，提高了系统定位精度，获得了很好的工程运用价值。此算法也可以推广到长、短超短基线阵水下跟踪领域，但在水下目标长距离和浅水区域跟踪时，不能解决水声信号反射引起的声线路径变化，存在一定的使用局限性。

参考文献：

[1] 刘伯胜,雷家煜. 水声学原理[M]. 哈尔滨:哈尔滨工程大学出版社,1993.

[2] 梁民赞,余毅,王黎明,等. 一种声线修正的查表方法[J].声学技术,2009,28 (4): 18-21.

[3] 王燕,梁国龙. 一种适用于长基线水声定位系统的声线修正方法[J]. 哈尔滨工程大学学报,2002,23(5): 32-35.