基于高斯核的波束形成

王超 邹丽娜（第七一五研究所 声纳技术重点实验室，杭州，310023）



基于高斯核的波束形成

王超 邹丽娜
（第七一五研究所 声纳技术重点实验室，杭州，310023）

摘要MVDR是波束形成常用的方法，但当信号到达方向与先验信息不一致时，MVDR的性能会出现下降，而将支持向量机应用于波束形成，并增加宽容性的限制条件，就可以解决这一问题，并能实现旁瓣控制。文章在此基础上考虑非线性处理，利用高斯核函数将信号从数据空间变换到再生核希尔伯特空间下进行处理，使得在阵元数小于干扰数目的情况下也能在干扰处陷零。

关键词高斯核；宽容性波束形成；支持向量机

波束形成是为了增强接收信号，并抑制干扰信号。依据这个标准出现了著名的MVDR算法，但是由于阵元位置和通道误差等原因，使得信号到达方向与先验信息不一致，此时它的性能就会变差，并且由于MVDR算法的旁瓣过高，在干扰很强的时候会对其性能产生影响。文献[1]中提出将支持向量机（SVM）引入到MVDR算法中来，它增加了额外的宽容性限制来减弱旁瓣，与此同时又允许信号到达方向与先验信息存在一定的误差，通过最小化风险函数来求解。把SVM引入MVDR中得到的解不再是满足限定条件的可行解，而是最接近于旁瓣等级的近似解。

通过高斯核可以把原有数据非线性变换到高维再生核希尔伯特空间（RKHS）中，在RKHS内做线性处理，最后把结果再变换到原始低维数据空间中。非线性映射的函数就称为核函数。RKHS有一个显著的特点，就是在其内部进行的内积运算可以通过对应的低维数据空间内的点运算得到。因此使得在高维RKHS的内积运算可以通过低维数据空间内运算得到，从而使映射到高维的问题可解。

对于探潜，如果探测海域内除了目标潜艇，还有很多行驶的船只，他们对目标形成干扰，并且当接收阵元比干扰数少时，常规线性算法就无法处理这个问题。因为如果有M个接收阵元，那么就有M−1个自由度可以来抑制干扰和噪声。如果此时干扰个数大于M−1，那么这个问题就没有办法解。为了解决这一问题，就需要考虑非线性运算，文献[3]已讨论如何将核方法引入到常规波束形成中。本文更进一步，将核方法引入到SVM宽容性波束形成算法中求解，并作了仿真分析。

1　MVDR波束形成

对于一个M阵元接收阵，其波束形成输出为

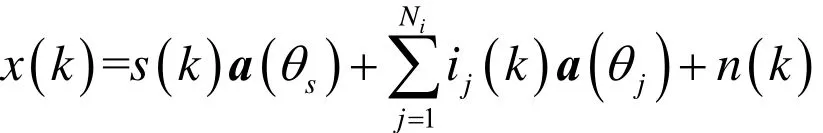
其中s(k)和ij(k)表示信号和干扰，n(k)代表噪声。信号和干扰到达角度分别为θs和θj,j=1,...,Ni。a(θs)和a(θj)代表相应角度的驾驶向量。

若信号到达角度已知，则可用经典的MVDR波束形成求解权重，即通过求解

得权重最佳解

其中Rx接收信号的协方差，可通过接收数据来计算。

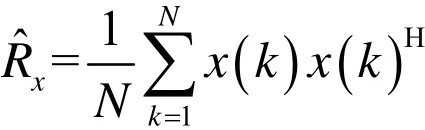
N是阵元采样点数。

对于旁瓣过高的问题，我们可以通过增加限制条件来抑制非信号到达方向的响应，所以问题就变为

式中P为约束条件数目，如果P>M此问题无解，此时可引入松弛变量，把等式限制条件变为不等式限制条件，就能使问题有解，此时的解是一个近似解，不再像原问题一样求的是最佳解。原有的MVDR问题变为

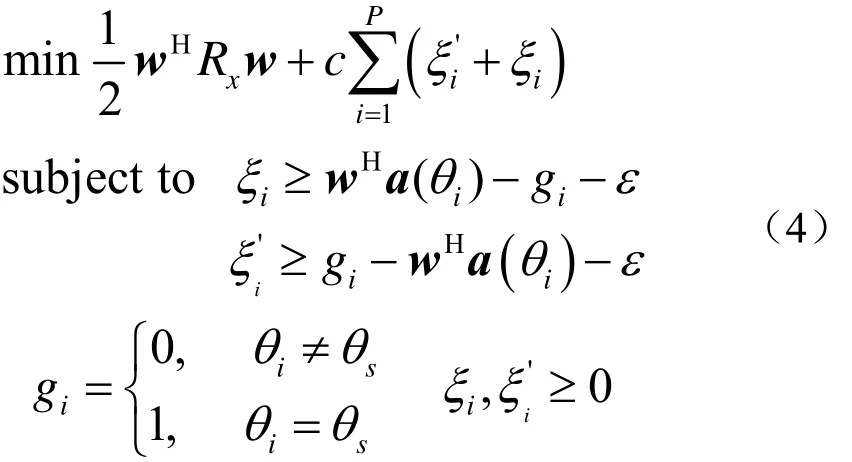
ε为期望响应允许的误差，ξi、为松弛因子，表示超过允许误差的部分，把此部分放入代价函数中，求代价函数极小值。这样就把等式约束变为不等式约束，使P>M情况下该问题仍有解。

MVDR的第二个问题：如果信号到达方向与先验信息不一致，上式中的约束条件就不对。在高SNR下，这种不一致会对MVDR产生显著的影响。

我们的宽容性处理方法就是设定先验角度，一定范围内的所有角度的期望响应都不为0。具体来说是将角度范围[−90°,90°]平均分为P份，对应的值为θi(1≤ i≤ P)，gi为角度θi的期望响应，θs为信号到达方向的先验信息，Δ为很小的正数，表示期望到达角可变动的范围，即假定在[θs−Δ ,θs+Δ ]内到达的角度都为真实的目标，所以体现了宽容性处理。具体问题转化为

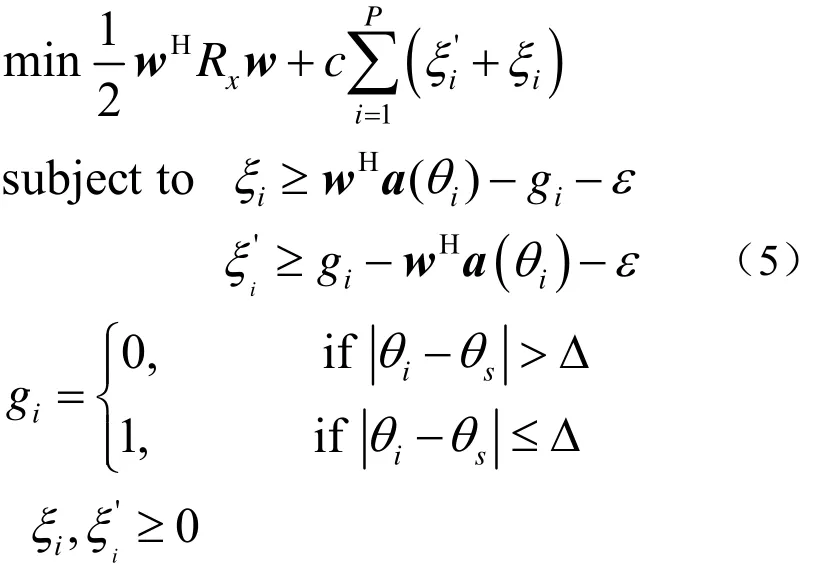
Δ的大小取决于先验信息的准确程度。

将上面表达式中的Rx做特征分解，再化简，得到的问题等价于一个支持向量回归问题（SVR）。可以通过二次最优化或者迭代加权最小二乘方法求解。

从图1可以看出，当干扰数目比较少时，输出信干比较大。而当干扰数目增大时，特别是干扰数大于阵元数，输出信干比一直在减小。这是因为SVM-MVDR中那么多的约束条件主要是针对非信号和干扰到达方向的角度。当() x k中干扰数目大于阵元数时，受维度所限，权重w不可能抑制所有干扰，使结果变差。下面提出的方法在干扰数目较大时仍能得到较好的结果。

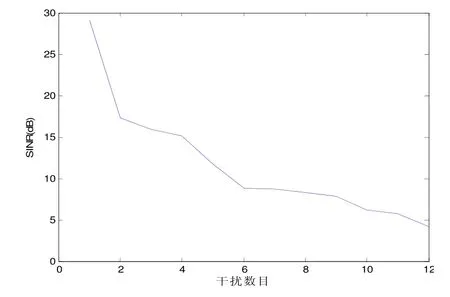
图1　SVM-MVDR信干比

2　干扰数大于阵元数的波束形成

如果将数据变换到高维特征空间就可以处理这个问题。对于任何一个正定对称的核k，我们可以对它做如下特征分解

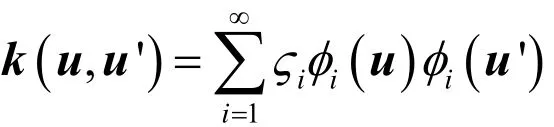
ςi、φi是核k(u,u ')的特征值和特征向量。u、u'是核函数的输入，他们是一个m×1的向量。我们要用的核函数为高斯核

设定F是核函数的特征函数所组成的空间，对于高斯核，它有无限个特征函数，其特征空间就是无限维。用ϕ(.)来表示一种映射，它将m×1的向量映射到特征空间F中。具体形式为，

其满足φ(u)Hφ (u')=k(u,u ')，所以只要知道所用的核函数形式，即使我们不知道φ(u)、φ(u')的具体形式，仍可以求出φ(u)Hφ (u ')的具体值，下面就是根据这一原理在高维特征空间处理数据。我们把驾驶向量映射到高维空间，即φ(a(θi))。接收信号的协方差R也要变换到高维特征空间中。具体形式为R=φφH/N，其中φ=[φ(x[1]) ,...,φ(x[ N ]) ]表示映射到RKHS下的点。

变换后的表达式为

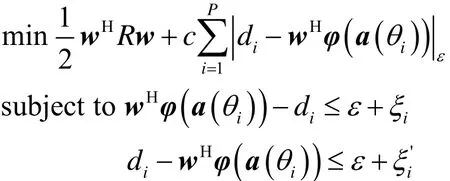
考虑实部和虚部误差，最终得到的目标函数为

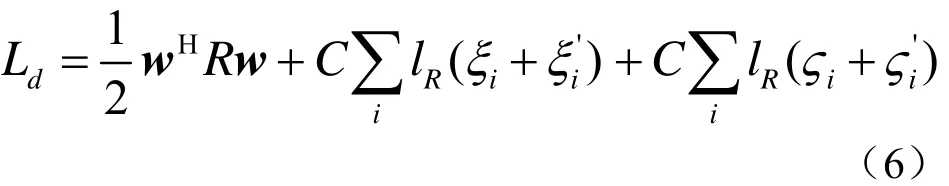
约束条件为

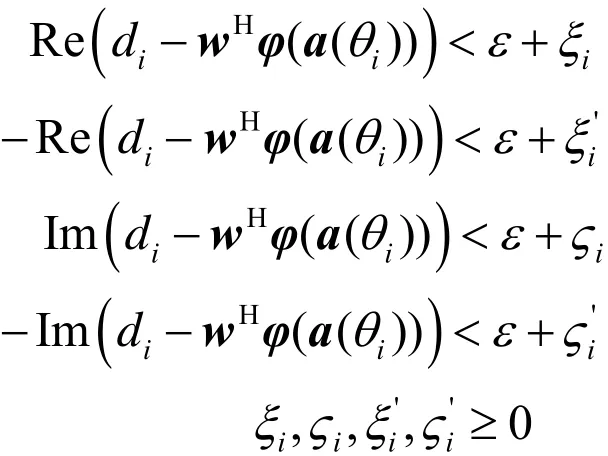
lR(.)为代价函数，ξi,ςi,为松弛因子，加入它以后将原来的等式约束变换为不等式约束，从而求得这些限定条件的最佳解。

应用拉格朗日乘数法可求得w =R−1φθψ，其中φθ=[φ(a(θ1)),...,φ(a(θi))]，其中ψ= α− α'−j(β− β'),α,α',β ,β'为四个限制条件所对应的拉格朗日乘数。并且

从这个式子可以看出即使我们写不出w的具体表达式仍能求出其相关运算结果。将此结果带入式（6）中，再进行特征分析，用Matlab的二次最优化函数求解。

3　仿真结果分析

对上述原理进行仿真分析，主要是将信号变换到高维去处理，具体过程如图2所示。

图2　原理示意图

用一个均匀线阵来进行仿真，阵元数为10，半波长布阵。源信号为独立同分布的BPSK信号，采用的信号快拍个数为50，仿真过程中加入高斯白噪声。设P=60，0°为信号到达方向，其响应值为1，其他方向到达的期望响应值为0。C和 ε为与环境有关的参数，可通过增加C或者减少ε来减小旁瓣等级。仿真过程中设定为1和0.001。

图3信号到达角度为0°，强度为10 dB，有6个干扰信号，到达角度分别为−75°、60°、−40°、−25°、35°、−60°，强度都为30 dB，此时阵元数大于干扰数。图中虚线是MVDR的结果，带o的线是Kernel-MVDR的结果，普通直线是SVM-MVDR的结果。从图中可以看出Kernel-SVM在所有算法中旁瓣最低，所以它的性能最好。

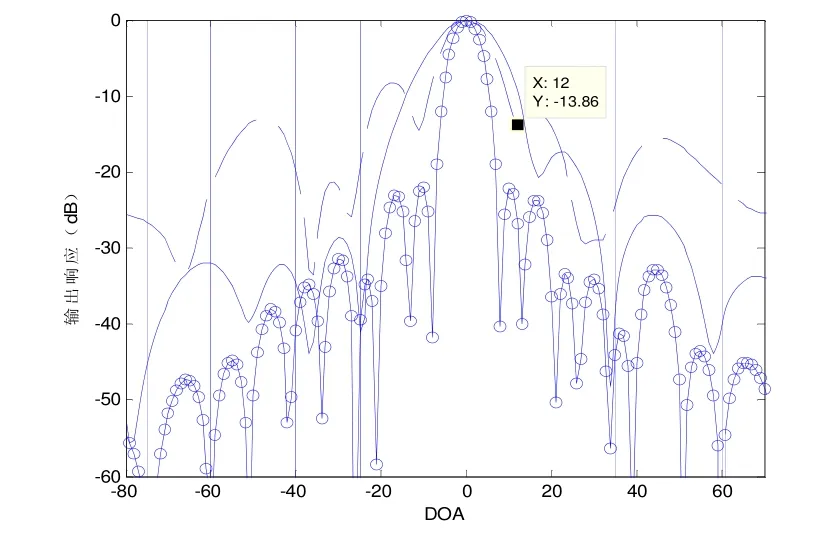
图3　6干扰无失配波束图

图4信号到达角度为0°，强度为10 dB，但是有12个干扰信号，到达角度分别为−75°、60°、−40°、30°、−10°、−25°、35°、−50°、80°、50°、−60°、−30°，强度都为30 dB，此时阵元数小于干扰数。图中*线是MVDR的结果，带o的线是Kernel-MVDR的结果，普通直线是SVM-MVDR的结果。

从图中可以看出MVDR与线性SVM算法都不能在所有点陷零，而Kernel-SVM算法在各个干扰角度的输出响应都有一定程度的下降，对比可得在干扰数目大于阵元数时Kernel-SVM算法依旧能达到比较好的性能。

图4　12干扰无失配波束图

图5中干扰情况与图4相同，但信号到达方向有2°失配情况下的波束图，虚线是MVDR的结果，带o的线是Kernel-MVDR的结果。图中0°线右边的那条线对应的是2°，可以看出Kernel-MVDR在信号到达的真实方向上有较强响应。

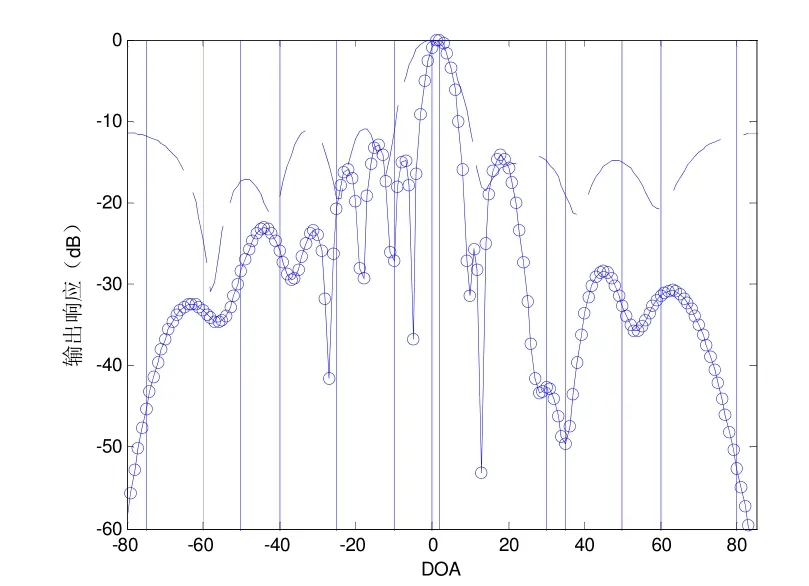
图5　12干扰2°失配波束图

图6为不同干扰个数所对应的输出信干比，从图中可以看出，在干扰数目较多时Kernel-SVM算法提供的性能比SVM算法要好。

图 6 信干比

4　结论

本文将数据从原始数据空间变换到再生核希尔伯特空间来求解多个不等式约束条件下的MVDR问题。从仿真结果可以看出把核方法引入到宽容性波束形成以后，可以在干扰数目多于阵元数时进行有效波束形成。

参考文献：

[1] CESAR C GAUDES,IGNACIO SANTAMARIA,FAVIER VIA,et al. Robust array beamforming with sidelobe control using support vector mechines[J]．IEEE Transactions on Signal Processing,2007,55(2):574-584．

[2] KONSTANTINOS SLAVAKIS,SERGIOS THEODORIDIS,ISAO YAMADA,et al. Adaptive constrained learning in reproducing kernel hilbert spaces:the robustbeamforming case[J]．IEEE Transactions on Signal Processing,2009,57(12).

[3]MANEL MARTINEZ RAMON,JOSE LUIS ROJOALVAREZ YAMADA,et al. Kernel antenna array processing[J]. IEEE Transactions Signal Process,2007,55(3): 642-650.