基于STM32的四旋翼飞行器的姿态最优估计研究*

何 川 ，李 智 ，，王勇军

（1.桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004；2.桂林航天工业学院无人遥测重点实验室，广西 桂林 541004）

0 引言

姿态最优估算是飞行器自主飞行的先决条件，在飞行过程中，实时准确地获得飞行器的姿态信息，可以决定飞行器的控制精度和稳定性[1]。随着微电子技术的发展，飞行器姿态解算系统普遍采用低成本的航姿参考系统（AHRS），其主要包括：基于微机电系统（MEMS）的三轴陀螺仪、三轴加速度计和三轴磁罗盘。由于系统机械结构和传感器自身三轴并非完全正交，引入了不正交误差，以及数据积分产生的发散误差和外部干扰产生的随机误差。因此要估计飞行器姿态的最优信息必须对多传感器进行误差处理，并寻求最佳数据融合算法。

目前国内对MEMS传感器姿态解算系统研究的常用算法有：扩展卡尔曼滤波、梯度下降法、互补滤波等。扩展卡尔曼滤波应用非常广泛，但为其建立可靠稳定的状态方程、确定合适的量测噪声和过程噪声协方差矩阵都比较困难。梯度下降法的好处在于姿态解算过程只有普通的乘法和加法运算，普通的微控制器即能满足算法要求，但难点在于构造合适的目标函数[2]。本系统在Mahony[3]提出的补偿滤波器的基础上进行优化，采用双环补偿滤波算法，外环引用重力场和地磁场进行补偿，内环引用重力场进行补偿，并将修正后的陀螺仪和磁罗盘进行互补滤波，以期得到最优姿态输出。

1 飞行器姿态描述

飞行器常用的姿态描述方法有欧拉角、方向余弦矩阵和四元数三种。三维空间中，飞行器有3个转动自由度，分别可以通过3个角度参数来描述飞行器的姿态，分别定义为：绕机体坐标系的Z轴转动为偏航角Ψ；绕X轴转动为横滚角φ；绕Y轴转动为俯仰角θ[4]。

如图1所示，飞行器在飞行过程中，地理坐标系b通过绕不同坐标轴三次连续转动来实现对机体坐标n的转换。第一次转动，OX0Y0Z0坐标系即地理坐标系ENU绕Z0轴转动Ψ角，得到坐标系OX1Y1Z0；第二次转动，OX1Y1Z0坐标系绕OX1轴转动φ角，得到坐标系OX1Y2Z2；第三次转动，OX1Y2Z2坐标系绕OY2轴转动 θ角，得到坐标系OXYZ，OY2轴即OY轴[5]。这三次坐标轴旋转可以用数学方法表述为3个独立的方向余弦矩阵。两个坐标系的转换可以用这3个独立变换矩阵的乘积表示：

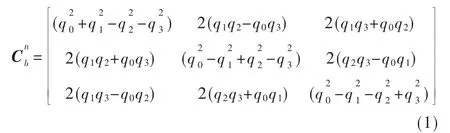
图1 飞行器坐标系和姿态角

由于载体的运动，四元数Q=[q0q1q2q3]T是变量，q0、q1、q2、q3是时间函数。 刚体绕瞬时转轴 n转过 σ角度来实现坐标的转换。为参考坐标系下的一个单位矢量，其角速度为：

机体坐标系n和地理坐标系b之间的变换也可以用四元数的三角形式表示[6]：

在忽略地球的自转和公转运动对四旋翼飞行器造成的影响，并假设飞行器为刚体运动且质量分布对称、均匀，中心为重心位置且不随着运动而发生变化[7]，则四元数矩阵表达式Q的微分方程解为：

2 飞行器姿态解算系统构建

2.1 系统硬件

本姿态解算系统硬件主要包括主控制器和航姿参考系统(AHRS)。其中主控器采用ST(意法半导体)公司的Cortex-M4为内核的32位ARM微控制器STM32F405RGT6；航姿参考系统采用2款高精度的姿态传感器，分别为：InvenSense公司的 MPU-6500和 ST公司的 LSM303D，构成了一个九轴的姿态测量系统。传感器均选用数字芯片，内部均集成有高精度的ADC。主控制器通过SPI总线，读取出传感器采集到的原始数据，然后通过四元数的坐标换算、姿态误差的双环PI控制和互补滤波解算出欧拉角。姿态解算系统框图如图2所示。

图2 姿态解算系统框图

2.2 传感器数据标定

在数据融合之前需要对传感器测量得到的原始数据进行标定，从而消除传感器的零点偏置误差。陀螺仪消除偏置误差的方法是保持器件水平位置不变，多次采集后求取输出平均值；加速度计消除偏置方法为八面校准法，将飞行器姿态解算系统保持机头方向不变，正面朝上、下、左、右、前、后和机头朝上、机头朝下。在这八种状态下分别测量三轴加速度计 ADC输出的X、Y、Z三轴的最大最小值，并与±1 g(重力加速度)所对应的ADC数值进行校准；磁罗盘零点数据误差采用椭圆假设法进行标定，将姿态解算系统分别在坐标系下XOY和XOZ两个平面内360°旋转，并将采集到的数据用MATLAB软件拟合成椭圆，然后修正椭圆的偏心和半径。

3 系统数据融合与姿态解算

系统姿态解算分为两个部分。第一部分是双环PI控制器修正数据融合后传感器偏差。第二部分为修正后的三轴陀螺仪与三轴磁罗盘进行互补滤波，消除磁罗盘的高频干扰，提高磁罗盘的响应能力和抗干扰能力。姿态解算流程图如图3所示。

3.1 双环PI控制器

陀螺仪可以快速响应机体的旋转，短时间误差较小、可信度高，但是存在温漂和零漂，以及积分误差随时间累积等因素影响。加速度计在静止的状态下漂移很小，倾角求解过程不存在积分误差，但是受到飞行过程中电机和机架的振动以及转动和运动加速度的干扰。磁罗盘测量得到的地磁向量在一定地理范围内可以认为不会发生改变，但是，磁罗盘容易受到硬磁场和软磁场的干扰。

图3 姿态解算流程图

因此，系统外环采用九轴姿态传感器（三轴加速度计、三轴磁罗盘和三轴陀螺仪）数据融合。由于磁罗盘容易受到干扰，有可能导致外环九轴数据融合后依旧存在较大误差，所以，内环采用六轴姿态传感器（三轴加速度计和三轴陀螺仪）数据融合，对数据融合后的传感器姿态偏差进行二次修正。

外环九轴姿态传感器数据融合，记在飞行器机体坐标系下 an=[axayaz]T和 mn=[mxmymz]T分别为加速度计和磁罗盘实际测量得到的重力向量和地磁向量。记vn=[vxvyvz]T和wn=[wxwywz]T是将地理坐标系下重力向量kb=[0 0 1g]T和地磁向量nb=[nx0nz]T（不考虑地理磁偏角因素，将机头固定向北）通过四元数坐标换算成机体坐标系下的重力向量和地磁向量。向量之间的误差为坐标轴的旋转误差，可以用向量的叉积en=[exeyez]T表示，如式（6）所示。由于陀螺仪是对机体直接积分，所以，陀螺仪的误差可以体现为机体坐标的误差。因此修正坐标轴的误差可以达到修正陀螺仪误差的目的，从而将加速度计和磁罗盘进行修正陀螺仪，实现了九轴的数据融合。即如果陀螺仪按照叉积误差的轴，转动叉积误差的角度，就可以消除机体坐标上实际测量的重力向量和地磁向量和坐标换算后的重力向量和地磁向量之间的误差。

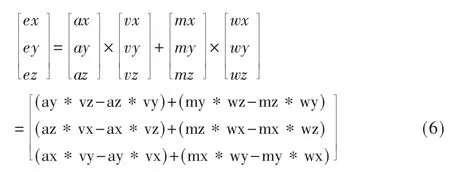
PI调节器的比例部分用于迅速纠正陀螺仪误差，积分部分用于消除稳态偏差[7]。通过大量实验验证后取PI调节器的比例系数为1.0，积分系数为0.2。陀螺仪经过外环PI控制器修正姿态误差后输出值为gn=[gxgygz]T：

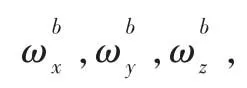
3.2 互补滤波

本系统姿态解算的第二部分是磁罗盘的修正，主要采用互补滤波算法。互补滤波算法简单可靠且对器件精度要求低。互补滤波的目的在于将陀螺仪和磁罗盘各自在频域角度上进行互补。因为磁罗盘动态响应能力差且易受外界环境的干扰，而陀螺仪动态响应快，故可在频域上将二者形成互补，即对磁罗盘低通滤波，对陀螺仪进行高通滤波。如图4所示，将修正后得到的陀螺仪数据与磁罗盘数据进行互补滤波，即可消除磁罗盘的高频干扰。

图4 互补滤波

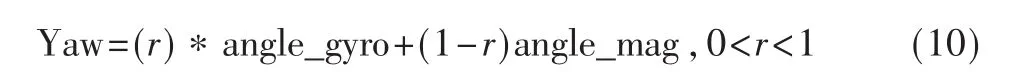
如式(10)所示，r为互补滤波中的权值，r值越大，证明陀螺仪占的权重越大。

4 姿态解算结果分析

为了验证姿态解算系统在多旋翼飞行器实际飞行过程中的性能，搭建了一个半实物仿真平台。将基于STM32的姿态解算系统的四旋翼飞行器机头朝向地理正北方，机架底部水平固定在万向节一端，万向节另外一端固定在水平的桌面上。启动四旋翼飞行器电机，将飞行器油门通道值保持在空中悬停状态，及四个螺旋桨产生的向上的合力等于飞行器自身重力。然后，通过串口读取出传感器采集到的原始数据以及姿态解算后的数据，并用MATLAB进行数据分析。

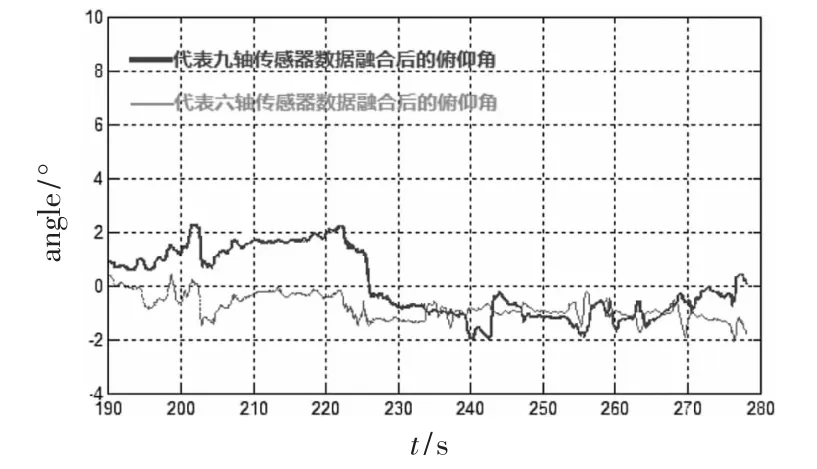
图5 俯仰角和横滚角

图5中采集的是模拟定点悬停时俯仰角和横滚角。由于单纯地通过陀螺仪采集得到的角速度进行积分得到角度会产生积分误差，并且积分误差会随着时间进行累加，所以未进行姿态解算所得到的姿态角零点误差会不断变大。图中的2条线分别代表姿态解算后的横滚角和俯仰角。由于采用了双环PI修正陀螺仪，所以姿态角零点误差与解算前相比不会随着时间累计不断变大。但是由于姿态解算系统处于四旋翼飞行器模拟定点悬停状态，所以，电机引起的机架振动、载体重力分布不均、机械连接处阻尼问题等因素，导致零点误差相对于水平放置在桌面上时的静态零点误差，偏差较大且波动相对厉害。零点误差基本稳定在±2.2°以内。随着时间的推移，零点误差逐步趋近平稳，可以满足四旋翼飞行器对姿态数据的要求。

图6中测试结果分别代表磁罗盘姿态解算前采集的数据和姿态解算后测量的数据。本系统采用的互补滤波算法中权值r取0.15，偏航角以磁罗盘采集的数据为主，数据融合后的陀螺仪只进行辅助修正。可以观测到细线代表的是没有使用滤波算法的磁罗盘测量的偏航角，零点误差相对较大，达到了±3°左右，而且上下波动也很大，表示磁罗盘受到外界环境严重干扰。粗线代表磁罗盘和陀螺仪经过互补滤波后采集得到的偏航角，消除了部分干扰信号，上下波动明显减弱，并且误差稳定保持在±1.7°以内。由于磁罗盘自身具有不可忽略的零位、灵敏度及非正交误差，因此通过软件算法无法彻底消除零点误差。

图6 偏航角

5 结论

旋翼飞行器飞行过程中获得姿态最优估计是飞行器系统稳定运行的根本保障。本文基于四元数坐标换算，将地理坐标系下的重力向量和地磁向量换算到机体坐标系下。然后通过修正坐标系旋转误差，实现了多传感器的数据融合，避免了陀螺仪零点积分误差的累积，并将修正后的陀螺仪与磁罗盘进行互补滤波，消除了磁罗盘的高频干扰。实验表明：经过双环PI控制修正姿态偏差的陀螺仪，俯仰角和横滚角零点动态误差保持在±2.2°左右；互补滤波后的磁罗盘消除了部分高频干扰，偏航角误差保持在±1.7°左右。本文设计的姿态解算系统较好地解决了噪声干扰与姿态最优估计问题，并在半实物仿真平台上得到了验证，实现了长时间稳定地输出准确可靠的姿态数据，满足了四旋翼飞行器飞行控制对姿态信息的要求。

[1]张浩，任芊.四旋翼飞行器航姿测量系统的数据融合方法[J].兵工自动化，2013，32（1）：28-31.

[2]杜杉杉，吴昊，张继文，等.一种面向 AHRS的改进互补滤波融合算法[J].国外电子测量技术，2015(3)：13-18.

[3]MAHONY R，HAMEL T.Complementary filters on the special orthogonal group[C].IEEE Transactions on Automatic Control，2008，53（5）：1203-1218.

[4]张天光，王秀萍，王丽霞.捷联惯性导航技术[M].北京：国防工业出版社，2007：15-16.

[5]邓正隆.惯性技术[M].哈尔滨：哈尔滨工业大学出版社，2006：10-11.

[6]李一波，宋述锡.基于模糊自整定PID四旋翼无人机悬停控制[J].控制工程，2013（5）：910-914.

[7]廖懿华，张铁民，廖贻泳.基于模糊-比例积分偏差修正的多旋翼飞行器姿态测算系统[J].农业工程学报，2014(20)：19-27.