超前探测巷道灾害性含导水构造的双频激电法
张金涛,周 游,刘志民,2,刘希高,吕一鸣,吴 淼
(1.中国矿业大学(北京)机电与信息工程学院,北京 100083;2.河北工程大学机电工程学院,河北邯郸 056038)
超前探测巷道灾害性含导水构造的双频激电法
张金涛1,周 游1,刘志民1,2,刘希高1,吕一鸣1,吴 淼1
(1.中国矿业大学(北京)机电与信息工程学院,北京 100083;2.河北工程大学机电工程学院,河北邯郸 056038)
摘 要:针对频率域煤巷超前探测灾害性含导水构造解析数学模型研究不足这一现状,基于空间电位拉氏方程和介质电阻率cole-cole模型,建立了煤巷超前探测灾害性含导水构造双频激电法的解析数学模型。通过模型分析,结果表明:双频激电法具有自动消除探测过程中对高低频电位相同干扰因素的影响,以及巷道空腔对探测结果的影响等优点;提出了利用所建解析数学模型,通过观测的视幅频率(PFE)数据快速确定灾害性含导水地质构造的厚度及其距掘进面的距离的方法。最后通过具体实施算例对所提方法进行了详细论证。
关键词:超前探测;含导水构造;双频激电法;解析模型
责任编辑:韩晋平
张金涛,周 游,刘志民,等.超前探测巷道灾害性含导水构造的双频激电法[J].煤炭学报,2015,40(8):1894-1899.doi:10.13225/ j.cnki.jccs.2015.0387
水害矿难对生命财产造成的损失在煤矿灾害事故中最为突出[1],为保证煤矿安全高效的生产,需要一种探测精度高、速度快和抗干扰能力强的超前探测方法来探明掘进工作面前方是否存在灾害性含导水地质构造。目前常用物探法主要分为地震类、电磁法类和电法类[2]。程久龙等[3]详细论述了地震类和电磁法类煤巷超前探测方法的缺点,此处不再赘述。目前用于煤矿井下的电法类超前探测方法主要是直流电法[4-5]。但是,直流点源场存在对掘进工作面前方异常体的弱敏感性[3]。总之,现有物探方法不能很好地解决煤巷综掘超前探测所面临的问题,探测理论有待深入研究。
何继善[6]详细论述基于激发极化理论的由高频和低频两种频率对组合的双频激电法的探测原理,并成功将其用于地面勘察金属矿和地下水。另外何继善指出双频激电法的优点是:探测精度高、速度快和抗干扰能力强,从这些优点看来双频激电法不失为一种较为理想的煤巷超前探测方法。但是,他并没有将该方法应用到煤巷超前探测。目前虽有学者将激发极化理论引入岩巷超前探测的研究,但他们的研究仅限于时域且检测的对象是半衰时和电阻率[7-9],相对频域而言时域抗干扰能力较差[6];张伟杰[10]和杜毅博[11]在双频激电法的基础上提出了电场激励法煤巷综掘超前探测技术,但其研究主要侧重点是软件仿真和数值模拟,并没有给出解析表达式。笔者分析巷道空腔对探测结果的影响之后,通过一系列的理论推导,给出了双频激电法煤巷综掘超前探测直接观测量——视幅频率(PFE)的解析数学表达式;PFE的解析表达式表明双频激电法在算法上可消除巷道空腔对探测效果的影响;最后,通过算例给出了根据现场观测的PFE曲线,快速确定灾害性含导水地质构造位置和厚度的方法。
1 巷道影响分析
目前有很多学者研究了巷道空腔对电法超前探测的影响,总结如下:王小龙等[12]在考虑巷道影响的电位数值模拟值与不考虑巷道影响的数值解析值的对比时发现,越靠近点电源的电位误差越大,距离点电源越远误差越小。在距离点电源2 m处绝对误差为0.117 548 V,相对误差为3.2%;在距离点电源15 m处绝对误差为4.6×10-5V,相对误差为0.01%;黄俊革等[13-14]指出巷道空腔只会影响极距较小时的视电阻率幅值,不会掩盖工作面前方地质体的异常响应;聂利超等[15]指出巷道空腔对视电阻率的影响主要集中在AM 距离较小的情况,而对视极化率的影响可以忽略;王永胜[16]和胡雄武等[17]指出巷道空间影响下的视电阻率与全空间视电阻率之间的线性关系:
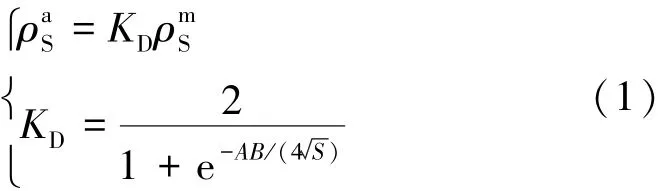
式中,ρS为视电阻率,Ω·m;上角a,m分别表示全空间和实测;KD为无量纲校正系数;AB为供电电极距,m;S为巷道截面积,m2。
前人的研究表明,小巷道空腔对现有探测方法的观测量的影响可以忽略,大巷道空腔的影响不可以忽略。但是双频激电法,由于其算法自身的特点,可以消除巷道空腔的对PFE的影响。这将在第2.3节得到证明。
2 解析模型推导
2.1 模型的建立
采用文献[13]中的建模方法,所建模型如图1所示。假设煤为各向同性介质,其电阻率为ρ1,极化率为η1;灾害性含导水地质构造为均匀无限大板状体,其厚度为a、电阻率为ρ2、极化率为η2、到掘进工作面中心的距离为d、与掘进工作面法线夹角为θ;灾害性含导水地质构造前面的煤的电阻率为ρ3、极化率为η3。后续参数分析过程中取ρ3=ρ2,η3=η2。
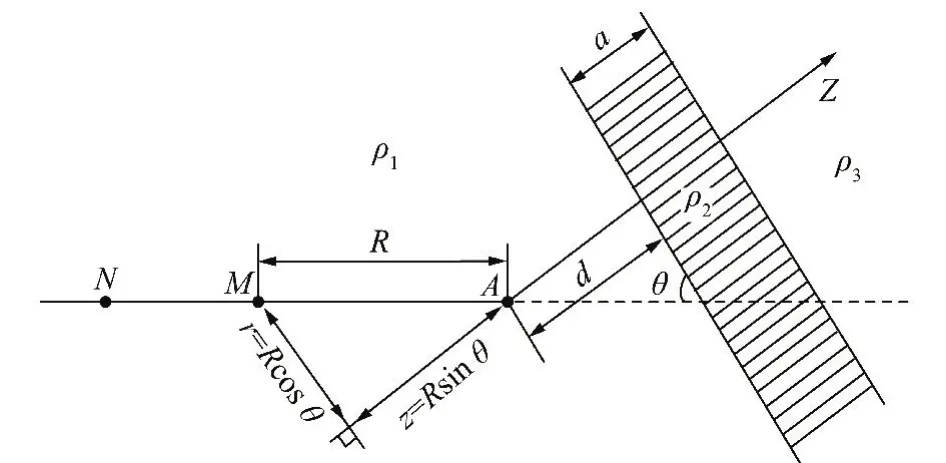
图1 巷道及灾害性含导水地质构造模型Fig.1 Model of the roadway and water-conducting or water-bearing structure
这样灾害性含导水地质构造将整个空间分成了3部分:有源ρ1介质区、无源ρ2介质区和无源ρ3介质区,且除A点外其他各点的电位Ui(i=1,2,3)都满足拉氏方程[13,18],即
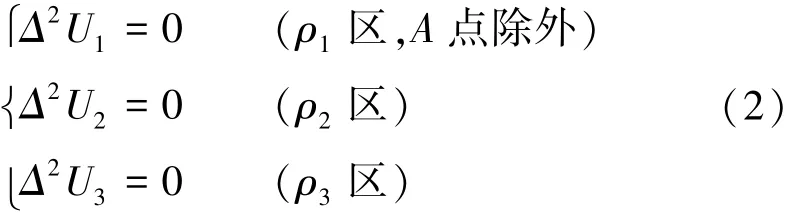
2.2 拉氏方程的解
建立柱坐标系,坐标原点位于A点,Z轴垂直于板状灾害性含导水地质构造且远离掘进工作面。由对称性可知,电位只与半径r和高度z有关,故电位U的拉氏方程可简化为
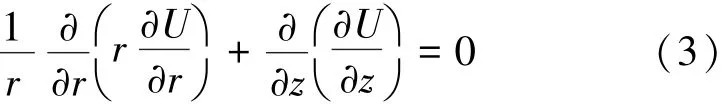
式(3)的一般解[13,19]为

式中,J0(mr)为零阶贝塞尔函数;A(m),B(m)为待定系数。
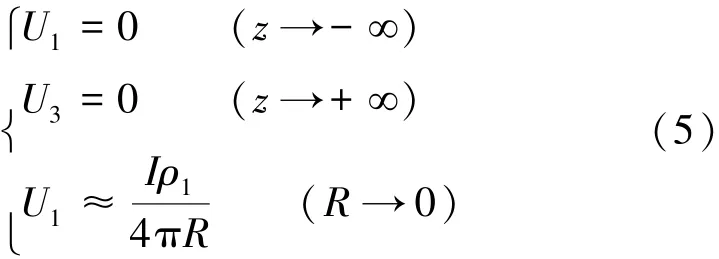
第3类边界条件形式为

根据式(5),(6)解方程(4)可得,采用二极装置在有源介质ρ1中的P点电位表达式为

式中,
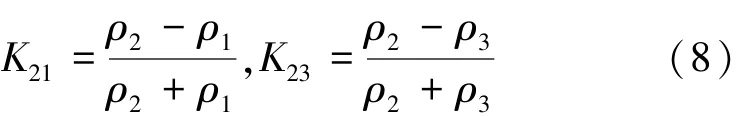
2.3 频率域参数推导
在频率域激电领域,用于表示介质电阻率的模型有阻容模型、德拜模型、瓦尔堡模型和cole-cole模型等[6]。其中cole-cole模型是以观察和实验为基础建立的模型,符合实际情况[20-22],其表达式为

式中,ρ(iω)为频率为ω时的介质电阻率,Ω·m;ρ0为零频时的电阻率,Ω·m;ω为激励的角频率,ω= 2πf,rad/ s;m为充电率,即极化率,为无量纲量;c为频率相关系数,一般0.1 由式(9)可得频率域中视电阻率的实部和虚部分别为 故ρ(iω)可写成 此时有 将式(13)带入式(8)整理得 其中,j=1,3,进一步整理式(14)得 将式(13),(16)带入方程(7)得 根据视幅频率(PFE)的定义[6]可得 式中,kf为分频系数,无量纲。 由式(20)可以看出在PFE值计算的过程中,存在两种频率的电位的减运算,那么对高低频电位相同的干扰因素便会借此消除,故双频激电法超前探测的探测精度高[6,10-11]。由于激励点电源的电流幅值是恒定的,所以由欧姆定律知 结合式(1)和式(21)可得 由式(22)可以看出在PFE值的计算过程中,消除了巷道空腔的影响系数KD。此外,巷道影响系数KD可能不仅有式(1)这一种表达形式。但是,无论KD的表达形式如何,只要它存在,那么经式(22)的计算KD的影响总会被消除。这体现了双频激电法的一大优点——消除巷道空腔对探测结果的影响。 分析了激励频率f、灾害性含导水地质构造的厚度a和灾害性含导水地质构造与掘进断面的距离d等主要参数与频率域超前探测观测参数PFE值的关系。关系曲线如图2所示。分析过程中,图2中除相应的分析参数外,其他参数选择如下:ρ10=ρ30= 100 Ω·m,ρ20=10 Ω·m,η1=η3=0.1,η2=0.5,kf= 13,a=2.5 m,d=25 m。 图2 频率f、倾角θ1、厚度a、距离d与PFE的关系Fig.2 Relationship between frequency f, inclination θ1,thickness a,distance d and PFE 从图2(a)可以看出,随f的大幅度变化,PFE极值点的位置并没有发生大幅度的变化;另外,随f的增大PFE先增后减,且使PFE整体最大的f在区间[0.001 Hz,0.1 Hz]。考虑到实际探测效率问题,建议在实际应用中将频率f定为1 Hz,分频系数kf定为13[6]。图2(b)~(d)的分析中f=1 Hz。 从图2(b)的分析表明随着灾害性含导水地质构造倾角θ1大幅度的变化,PFE极值的大小和位置变化都很小。经计算,θ1从30°增加到90°时PFE只减小了5.6%。如此小幅度变化极易被实际观测误差淹没,所以实际探测过程中不能够根据现有的观测参数确定灾害性含导水地质构造的倾角。 从图2(c),(d)可以看出PFE的极值和极值位置都随灾害性含导水地质构造厚度a和灾害性含导水地质构造到掘进面距离d的变化而大幅度变化。在实际应用中煤的电性参数以及矿井水的电性参数可以现场测得。然后再利用本文的解析数学模型就可以做出类似图2(c),(d)中的若干条相应极值拟合曲线图。然后利用现场测得的PFE极值大小及其位置,便可以快速得到灾害性含导水地质构造的厚度a和其到掘进工作面的距离d这两个需要探明的关键参数。具体方法见第4节算例分析。 算例中模型参数如下:ρ10=ρ30=100 Ω·m,ρ20= 10 Ω·m,η1=η3=0.1,η2=0.5,kf=13,a=2.5 m;d= 24 m。“实测”PFE曲线是在相应测点的理论PFE基础上,随机增加0~6%的误差后获得的。 图3中d和a分别标注的是相应模型参数下与图2(a),(b)中相同的理论PFE极值拟合曲线。在图3不难发现,“实测”PFE曲线的极值存在于椭圆形虚线框内。故根据“实测”PFE曲线可判定:2 m≤a(实测)≤3 m、22 m≤d(实测)≤26 m,取中间平均值得:a(实测)= 2.5 m、d(实测)= 24 m。 图3 具体实施算例Fig.3 Concrete example (1)双频激电法可以消除高低频电位相同干扰因素和巷道空腔对超前探测结果的影响。 (2)双频激电法超前探测的直接观测参数PFE的极值的大小和位置,随灾害性含导水地质构造的位置d和厚度a的变化呈规律性大幅度变化。 (3)通过这种变化规律利用PEF极值的大小和位置,可以反求出灾害性含导水地质构造的位置d和厚度a这两个巷道超前探测的目的性参数。 参考文献: [1]武 强.我国矿井水防控与资源化利用的研究进展、问题和展望[J].煤炭学报,2014,39(5):795-805. Wu Qiang.Progress,problems and prospects of prevention and control technology of mine water and reutilization in China[J].Journal of China Coal Society,2014,39(5):795-805. [2]刘盛东,刘 静,岳建华.中国矿井物探技术发展现状和关键问题[J].煤炭学报,2014,39(1):19-25. Liu Shengdong,Liu Jing,Yue Jianhua.Development status and key problems of Chinese mining geophysical technology[J].Journal of China Coal Society,2014,39(1):19-25. [3]程久龙,李 飞,彭苏萍,等.矿井巷道地球物理方法超前探测研究进展与展望[J].煤炭学报,2014,39(8):1742-1750. Cheng Jiulong,Li Fei,Peng Suping,et al.Research progress and development direction on advanced detection in mine roadway working face using geophysical methods[J].Journal of China Coal Society, 2014,39(8):1742-1750. [4]韩德品,李 丹,程久龙,等.超前探测灾害性含导水地质构造的直流电法[J].煤炭学报,2010,35(4):635-639. Han Depin,Li Dan,Cheng Jiulong,et al.DC method of advanced detecting disastrous water-conducting or water-bearing geological structures along same layer[J].Journal of China Coal Society,2010, 35(4):635-639. [5]张平松,李永盛,胡雄武.巷道掘进直流电阻率法超前探测技术应用探讨[J].地下空间与工程学报,2013,9(1):135-140. Zhang Pingsong,Li Yongsheng,Hu Xiongwu.Application and discussion of the advanced detection technology with DC resistivity method in tunnel[J].Chinese Journal of Underground Space and Engineering,2013,9(1):135-140. [6]何继善.双频激电法[M].北京:高等教育出版社,2005. [7]李术才,刘 斌,李树忱,等.基于激发极化法的隧道含水地质构造超前探测研究[J].岩石力学与工程学报,2011,30(7): 1297-1309. Li Shucai,Liu Bin,Li Shuchen,et al.Study of advanced detection for runnel water-bearing geological structures with induced polarization method[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(7):1297-1309. [8]聂利超.隧道施工含水构造激发极化定量超前地质预报理论及其应用[D].济南:山东大学,2014. [9]刘 斌.基于电阻率法与激电法的隧道含水地质构造超前探测与突水灾害实时监测研究[D].济南:山东大学,2010. [10]张伟杰.动态定向电场激励法煤巷掘进超前探测技术研究[D].北京:中国矿业大学(北京),2012. [11]杜毅博.电场激励法煤巷综掘超前探测机理研究及原理样机研制[D].北京:中国矿业大学(北京),2014. [12]王小龙,冯 宏,李 萍,等.矿井电阻率超前探测正演模拟[J].煤炭科学技术,2011,39(11):112-117. Wang Xiaolong,Feng Hong,Li Ping et al.Application of COMSOL multiphysicsto pilot detection positive evolution of mine resistivity[J].Coal Science and Technology,2011,39(11):112-117. [13]黄俊革,王家林,阮百尧.坑道直流电阻率法超前探测研究[J].地球物理学报,2006,49(5):1529-1538. Huang Junge,Wang Jialin,Ruan Baiyao.A study on advanced detection using DC resistivity method in tunnel[J].Chinese Journal of Geophysics,2006,49(5):1529-1538. [14]黄俊革,阮百尧,王家林.坑道直流电阻率法超前探测的快速反演[J].地球物理学报,2007,50(2):619-624. Huang Junge,Ruan Baiyao,Wang Jialin.The fast inversion for advanced detection using DC resistivity in tunnel[J].Chinese Journal of Geophysics,2007,50(2):619-624. [15]聂利超,李术才,刘 斌,等.隧道激发极化法超前探测快速反演研究[J].岩土工程学报,2012,34(2):222-229. Nie Lichao,Li Shucai,Liu Bin,et al.Fast inversion for advanced detection using induced polarization in tunnel[J].Chinese Journal of Geotechnical Engineering,2012,34(2):222-229. [16]王永胜.井下直流电法解释软件系统[J].煤田地质与勘探, 1998,26(S1):52-54. Wang Yongsheng.System of interpreter of direct current method in coal mine[J].Coal Geology & Explorations,1998,26(S1):52-54. [17]胡雄武,张平松,吴荣新,等.矿井多极供电电阻率法超前探测技术研究[J].地球物理学进展,2010,25(5):1709-1715. Hu Xiongwu,Zhang Pingsong,Wu Rongxin,et al.Study on the advanced detection technique by multi-electrode direct current resistivity in mines[J].Progress in Geophysics,2010,25(5):1709-1715. [18]李金铭.地电场与电法勘探[M].北京:地质出版社,2005. [19]顾 樵.数学物理方法[M].北京:科学出版社,2012. [20]杨振威,郑 伟,李晓斌,等.频谱激电法的发展与展望[J].物探与化探,2015,39(1):22-28. Yang Zhenwei,Zheng Wei,Li Xiaobin,et al.The development and prospect of the spectral induced polarization method[J].Geophysical and Geochemical Exploration,2015,39(1):22-28. [21]Eirik G F.A physical basis for the Cole-Cole description of electrical conductivity of mineralized porous media [J].Geophysics, 2013,78(5):355-368. [22]Andrey T,Konstantin T.On the use of the Cole-Cole equations in spectral induced polarization[J].Geophysical Journal International,2013,195(1):352-356. Zhang Jintao,Zhou You,Liu Zhimin,et al.Dual-frequency induced polarization method for advanced detection on disastrous water-conducting or water-bearing structure in roadway[J].Journal of China Coal Society,2015,40(8):1894-1899.doi:10.13225/ j.cnki.jccs.2015.0387 Dual-frequency induced polarization method for advanced detection on disastrous water-conducting or water-bearing structure in roadway ZHANG Jin-tao1,ZHOU You1,LIU Zhi-min1,2,LIU Xi-gao1,LÜ Yi-ming1,WU Miao1 (1.School of Mechanical Electronic & Information Engineering,China University of Mining and Technology (Beijing),Beijing 100083,China;2.Mechanical and Electrical Engineering Institute,Hebei University of Engineering,Handan 056038,China) Abstract:In order to overcome the problem with the inadequate study on frequency domain advanced detection on the disastrous water-conducting or water-bearing structure in roadway,a mathematical model of Dual-frequency induced polarization (IP) method was built based on the Laplace equation in spatial potential field and cole-cole model.Through model analysis,it manifests that the dual frequency IP method has the advantages of automatic elimination of the same interference factor for high and low frequency potential,and the influence of the tunnel cavity on the detection results.The thickness and position of water-conducting or water-bearing structure can be quickly obtained by PFE with the analytical model.Finally,a case study demonstrates the process of determining the thickness and position. Key words:advanced detecting;water-conducting or water-bearing structure;dual-frequency IP method;analytical model 作者简介:张金涛(1985—),男,河北邢台人,博士研究生。Tel:010-62339112,E-mail:jtzhangwhy@163.com 基金项目:国家高技术研究发展计划(863)资助项目(2012AA06A405) 收稿日期:2015-03-25 中图分类号:P631.4 文献标志码:A 文章编号:0253-9993(2015)08-1894-06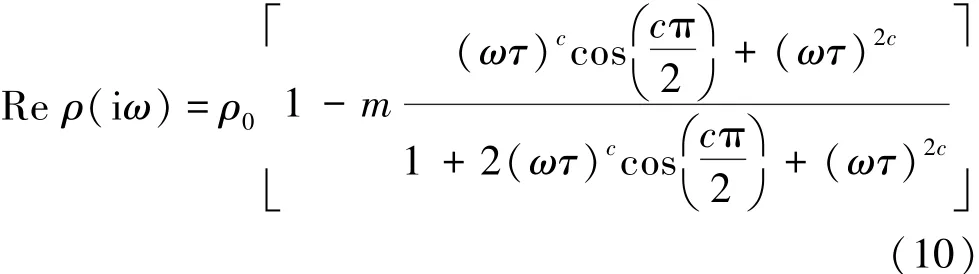
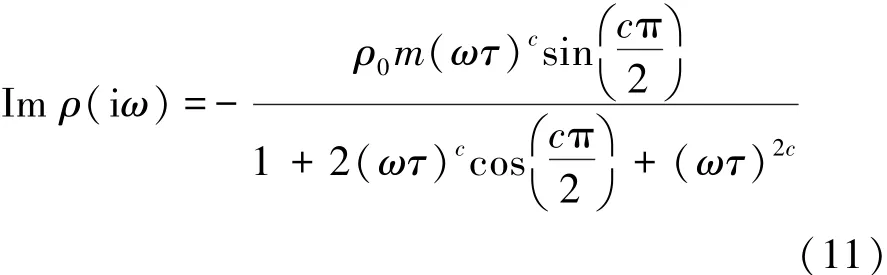
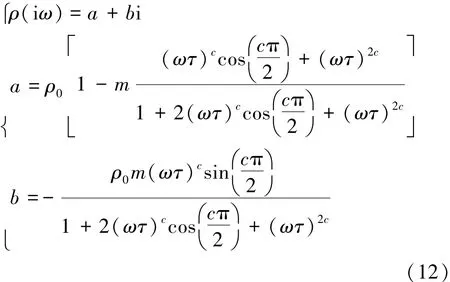
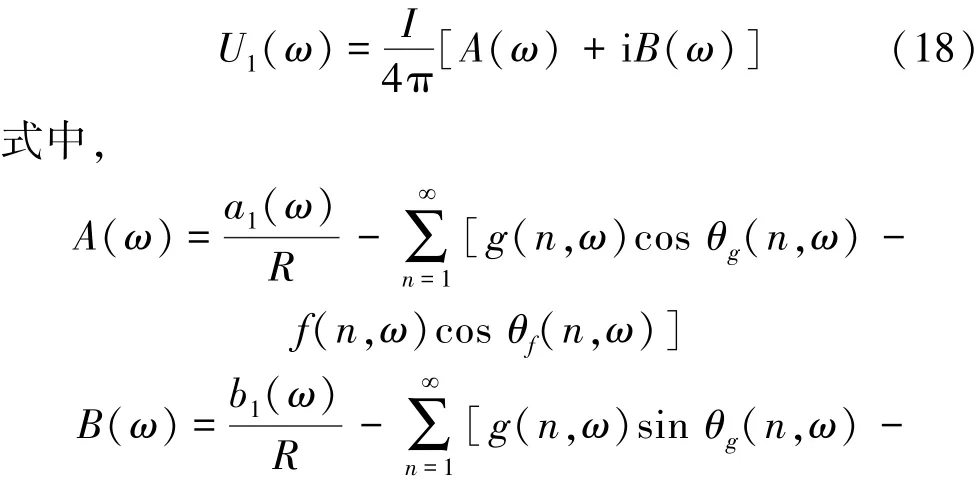
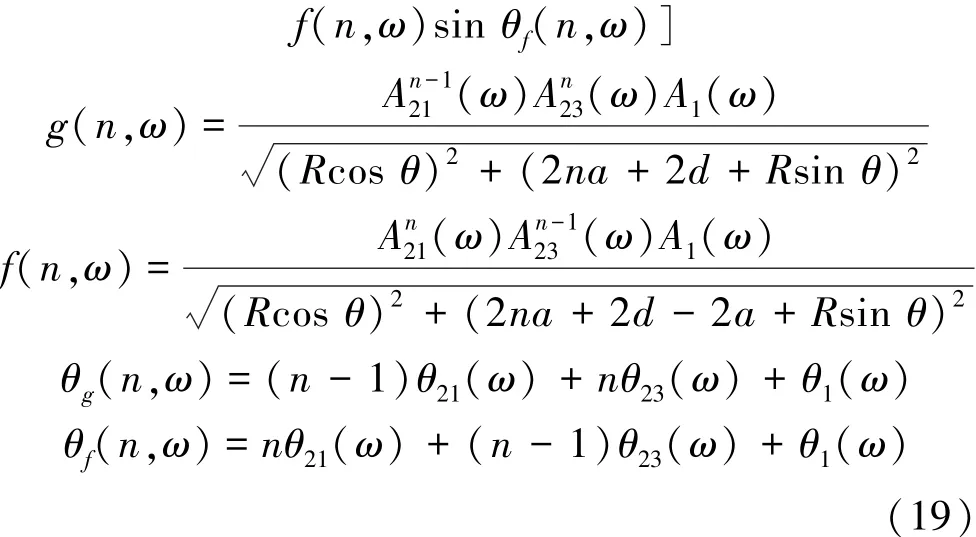
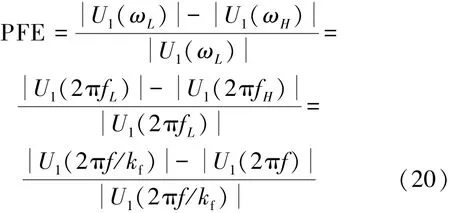
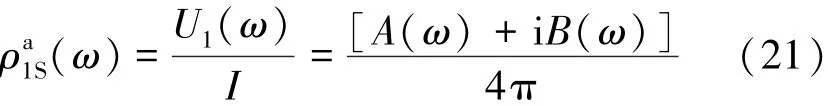
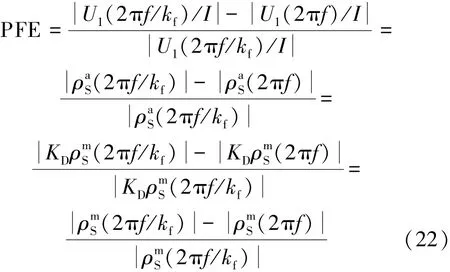
3 参数分析

4 算例分析
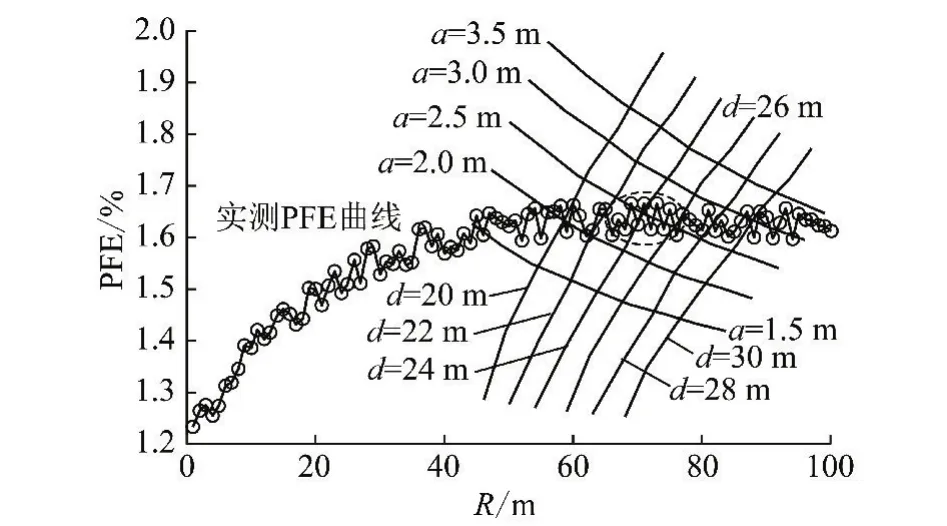
5 结 论

