侧斜变化对螺旋桨水动力及变形振动特性的影响

张瑞，王先洲，张志国，江伟健，陶铸

华中科技大学船舶与海洋工程学院，湖北武汉430074

侧斜变化对螺旋桨水动力及变形振动特性的影响

张瑞，王先洲，张志国，江伟健，陶铸

华中科技大学船舶与海洋工程学院，湖北武汉430074

由于艇后伴流场的不均匀性，螺旋桨运转时，周期性变化的载荷与桨叶结构的耦合作用会使桨叶发生变形。基于ANSYS Workbench平台，利用ACT_Transient FSI技术，将Fluent结果直接转换导入有限元求解器来计算螺旋桨结构响应，从而实现艇后螺旋桨瞬态单向的耦合分析。以DTMB 4381，DTMB 4382和DTMB 4383桨为研究对象，对艇后螺旋桨的水动力特性及桨叶的变形等进行数值模拟。结果表明：随着螺旋桨侧斜角的增加，脉动推力振荡明显减弱，桨叶最大变形量增加，但桨叶振动明显减弱。

螺旋桨；流固耦合；脉动推力；变形特性

0 引 言

螺旋桨是目前使用得最广泛的船舶推进器，不少学者在其水动力性能、空泡和噪声等方面进行了大量的计算与研究，同时对螺旋桨的桨叶振动也给予了关注。由于伴流场的不均匀性，螺旋桨运转时会产生非定常的推力与转矩，从而引起桨叶和轴系的振动，而螺旋桨侧斜的变化又会对桨的脉动推力产生影响，进而影响到桨叶的振动。

在国内外的螺旋桨流固耦合研究领域，Georgiev等［1］基于势流理论建立流固耦合算法，对螺旋桨进行了水动力计算；Young［2］研究了面元法与软件ABAQUS耦合的螺旋桨流固耦合计算方法；Lin等［3］采用升力面法和九节点退化壳单元耦合算法，推导了求解复合材料螺旋桨水动力性能的算法；孙海涛和熊鹰等［4-7］在复合材料螺旋桨流固耦合算法方面进行了大量研究，建立了较为完善的流固耦合控制方程和求解算法，给出了复合材料螺旋桨预变形设计的原则；洪毅等［8］采用将基于RANS方程的计算流体力学与有限元方法相结合的方法，对复合材料螺旋桨的敞水性能进行了研究；张帅等［9-10］发展了应用CFD/CSD耦合方式分析螺旋桨流固耦合特性的求解方法；吴建岚和周振龙［11］应用ANSYS-CFX技术对复合材料螺旋桨进行了双向流固耦合计算。

本文将基于非定常RANS方法与有限元方法相结合的方法，利用商业软件ANSYS Workbench中的FSI瞬态流固耦合技术，以螺旋桨DTMB 4381，DTMB 4382和DTMB 4383为对象，研究侧斜变化对螺旋桨变形特性的影响，包括变形量和桨叶振动等。

1 算例说明

以直径0.304 8 m的DTMB 4381，DTMB 4382和DTMB 4383模型为计算对象，侧斜角分别为0°，36°和72°，进速系数J=0.889，来流速度2.71 m/s，转速600 r/min；Suboff模型艇体总长4.356 m，最大直径0.508 m。螺旋桨模型如图1所示。

图1 不同侧斜螺旋桨模型图Fig.1 The models of DTMB 4381，DTMB 4382 and DTMB 4383

2 网格与求解设置

将整个流场划分为与螺旋桨同轴线的内、外2个圆柱体区域：在螺旋桨所在旋转区域，采用网格较密的非结构化网格；在艇体所在区域，采用网格尺度稍大的结构化网格，内、外域之间通过定义interface传递数据。艇体带桨网格如图2所示。

图2 Suboff艇体及周围网格划分Fig.2 The mesh of Suboff hull and propeller

桨叶在外载荷作用下将产生弯扭耦合变形。进行变形计算时，采用8节点实体单元对桨叶进行有限元剖分，单元之间通过节点相互连接，划分的这些单元集合的整体效果与原来的连续体的效果基本相同。螺旋桨DTMB 4381的有限元网格如图3所示。

螺旋桨材料设为铜合金，材料密度为8 300 kg/m3，杨氏模量E=110 GPa，泊松比为0.34。

桨叶为流固耦合面，桨毂为位移固支约束，如图4所示，旋转中心在螺旋桨轴线处，施加的螺旋桨转速与流体求解中的螺旋桨转速相同，可保证流固耦合计算压力加载点完美匹配。

图3 DTMB 4381桨的有限元网格Fig.3 Finite element mesh of DTMB 4381

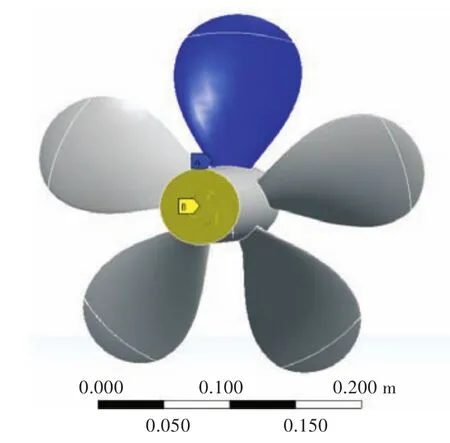
图4 DTMB 4381桨的流固耦合面设置Fig.4 Fluid-structure interaction surface of DTMB 4381

3 结果分析

3.1 敞水结果验证

对敞水模型进行网格独立性检验，确定使用的网格方案，螺旋桨旋转域网格60万，外流域140万。螺旋桨DTMB 4381的敞水性能计算结果与试验结果对比如表1所示。

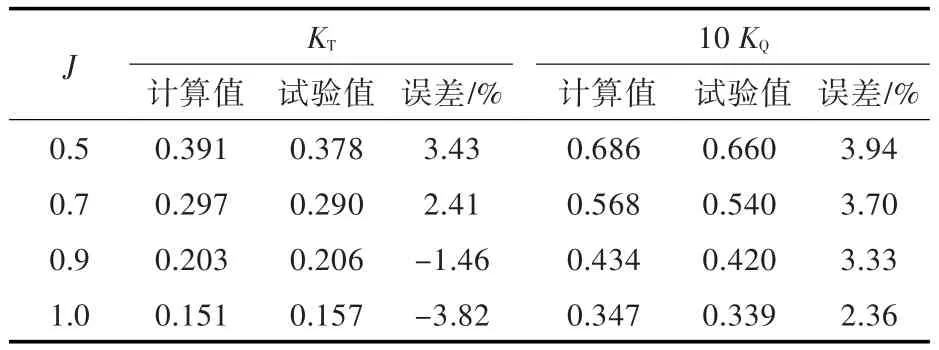
表1 DTMB 4381的敞水性能比较Tab.1 The open water performance results of DTMB 4381

表1给出了螺旋桨DTMB 4381在J=0.5，0.7，0.9和1.0这4个进速系数下的水动力系数计算结果，通过对比试验结果［12］，发现在常用进速系数区间的预报误差可控制在4%以内，并且比较稳定，确认了数值模拟的准确性与可靠性。

3.2 螺旋桨脉动力

对艇后螺旋桨脉动推力采用滑移网格进行非定常计算。图5～图7所示为不同侧斜螺旋桨的整桨脉动推力曲线，从中可以注意到，当螺旋桨轴向推力以近似50 Hz的频率振荡时，DTMB 4381的激振力幅值与时均值之比为0.49%，DTMB 4382的激振力幅值与时均值之比为0.31%，DTMB 4383的激振力幅值与时均值之比为0.11%，振荡的峰值最大约为螺旋桨轴向推力时均值的1%。计算结果与Liefvendahl等［13］计算的相当，Liefvendahl等计算的轴向力峰值约为推力的2%～3%，其原因可能在于每个桨叶的网格划分不一致，以及使用网格重塑使得每个时间步所计算的网格不同而导致离散误差。结果表明，侧斜对螺旋桨激振力幅值的影响非常明显，随着侧斜的增加，激振力震荡明显减弱。

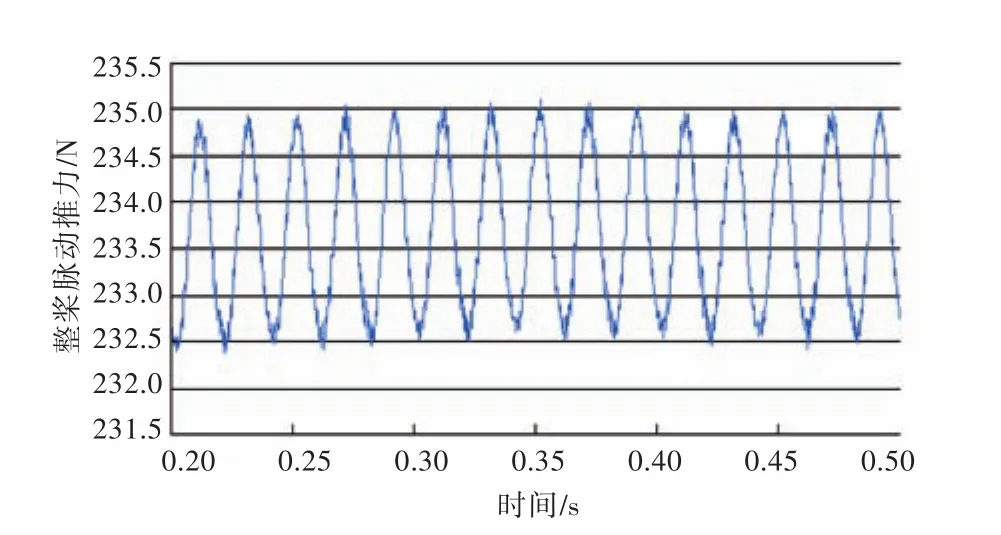
图5 DTMB 4381整桨脉动推力曲线Fig.5 Time history curve of propeller thrust of DTMB 4381

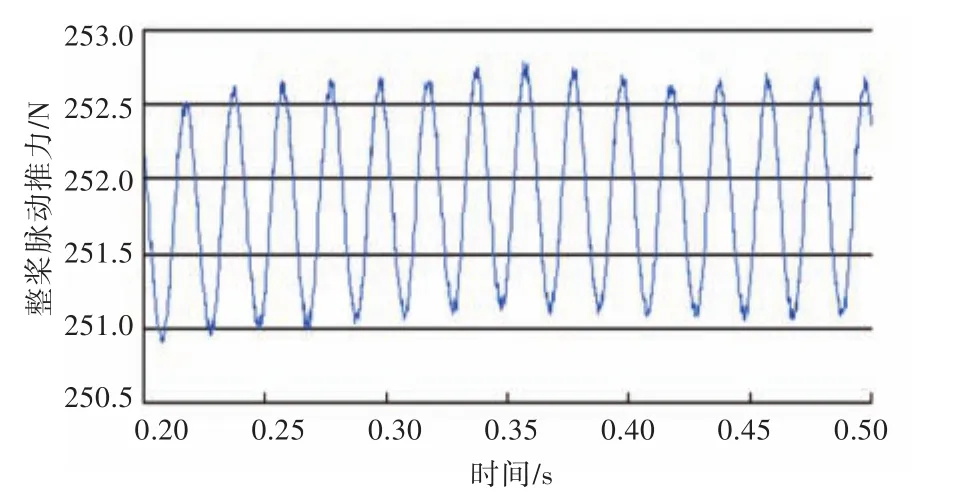
图6 DTMB 4382整桨脉动推力曲线Fig.6 Time history curve of propeller thrust of DTMB 4382

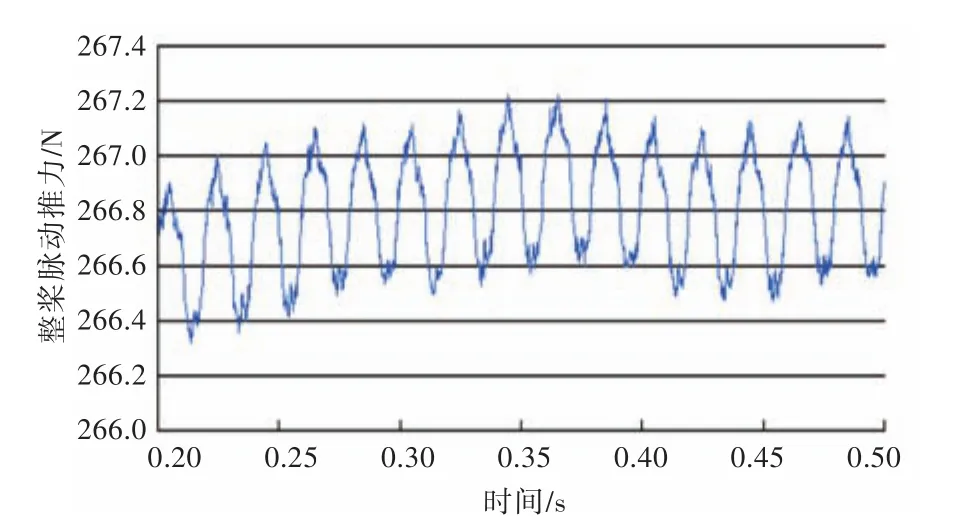
图7 DTMB 4383整桨脉动推力曲线Fig.7 Time history curve of propeller thrust of DTMB 4383

图8～图10所示为不同侧斜螺旋桨的压力分布图。由图可发现，压力峰值位于压力面近导边处，与实际桨叶表面的压力分布规律相符，表明本文所用的仿真方法能够很好地捕捉到桨叶吸力面与压力面的压力分布。

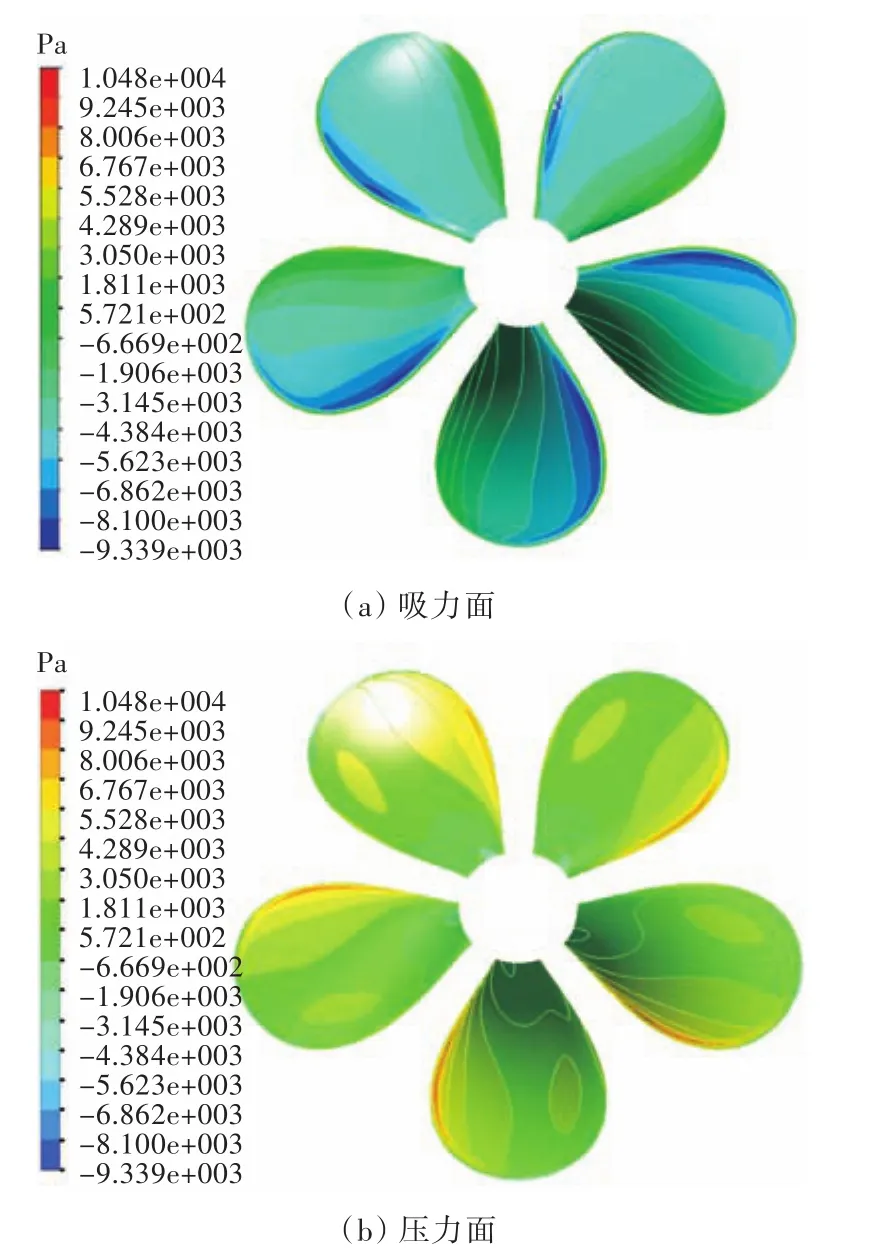
图8 DTMB 4381吸力面与压力面压力分布图Fig.8 Pressure contours of DTMB 4381

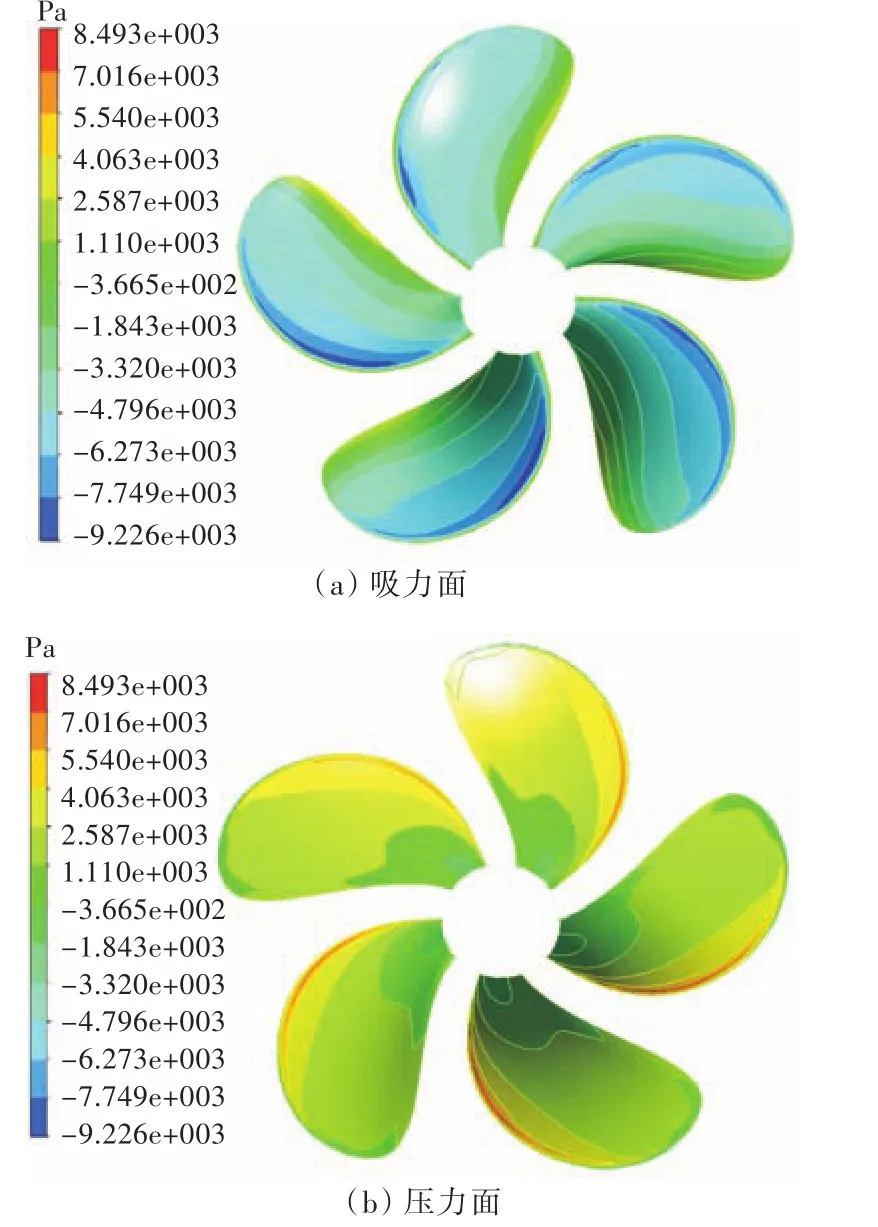
图9 DTMB 4382吸力面与压力面压力分布图Fig.9 Pressure contours of DTMB 4382

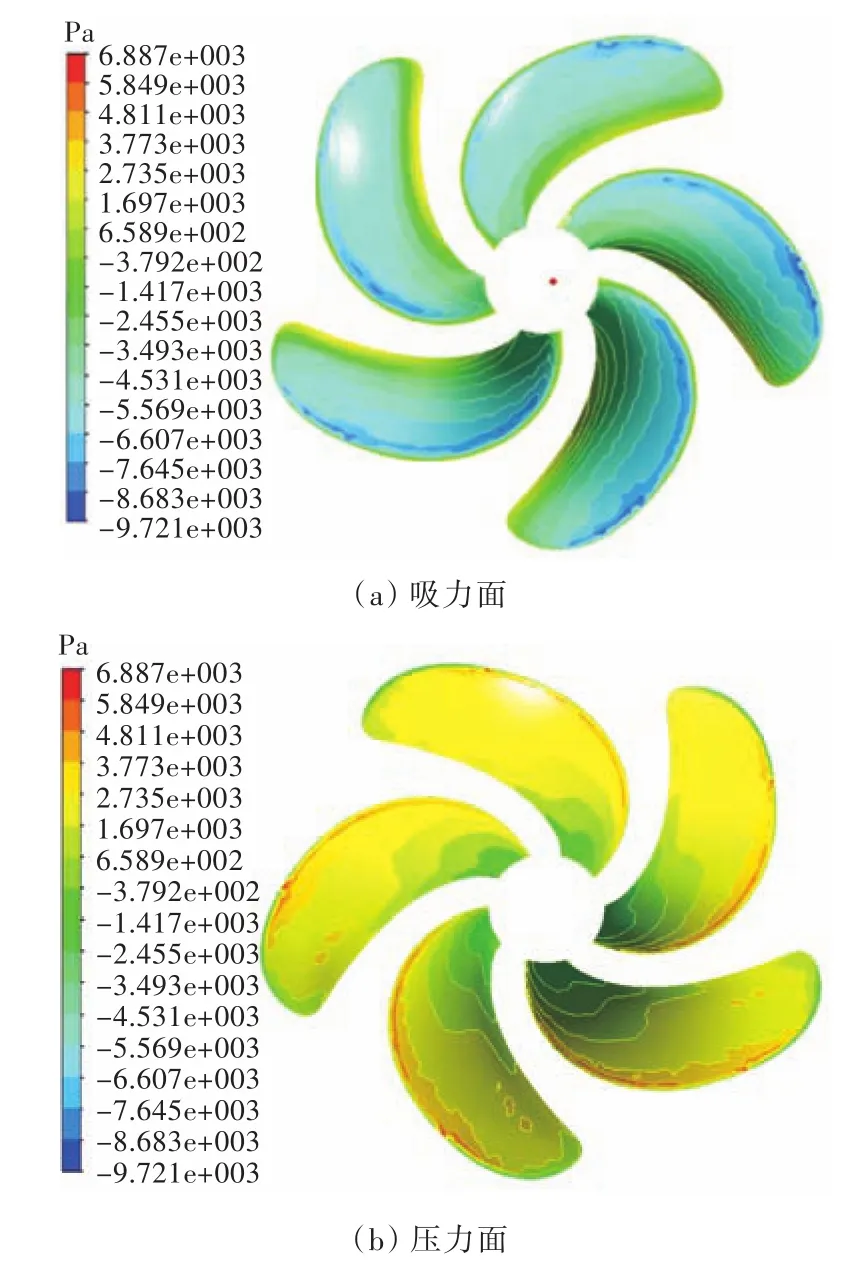
图10 DTMB 4383吸力面与压力面压力分布图Fig.10 Pressure contours of DTMB 4383

本文采用流固耦合计算桨叶变形研究的是单个桨叶的变形振动，所以需仔细分析单桨叶推力随时间变化的情况。图11和图12所示为桨叶初始相位角位置示意图及DTMB 4381单个桨叶在不同相位角处轴向推力的变化曲线。从图12中可以清晰地看出十字形尾翼对螺旋桨推力变化的影响，同时在90°相位角处，马蹄涡对推力的影响也很清晰。

图13所示为不同侧斜螺旋桨单个桨叶轴向推力随时间变化的曲线图。从图中可以对比看出，随着螺旋桨侧斜的增加，单桨叶的推力震荡明显减弱，且在90°相位角处马蹄涡对推力的影响也明显减弱。

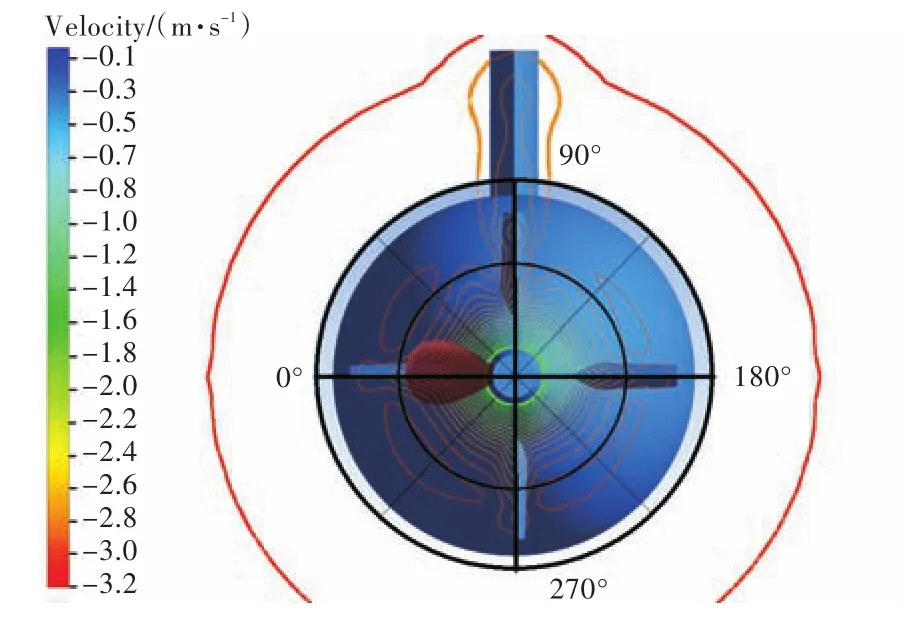
图11 桨叶初始相位角示意图Fig.11 The initial phase angle of blade

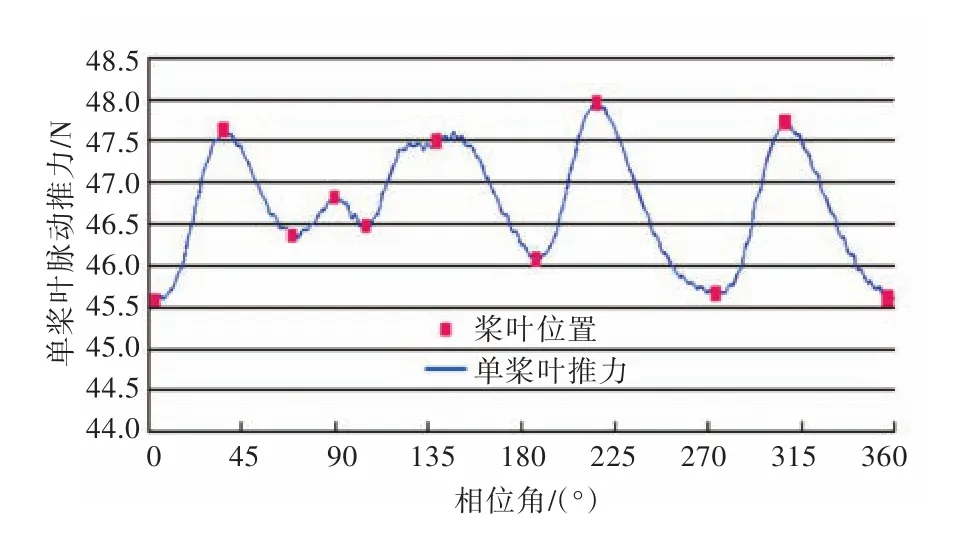
图12 桨叶旋转一周不同位置处的推力Fig.12 The thrust of blade at different locations

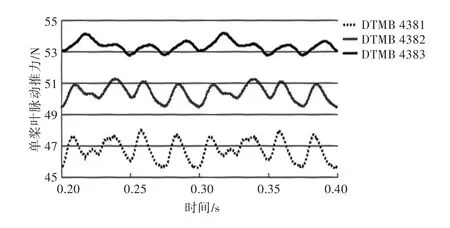
图13 不同侧斜螺旋桨单桨叶推力曲线Fig.13 The thrust curves of DTMB 4381，DTMB 4382 and DTMB 4383

3.3 螺旋桨桨叶变形

螺旋桨桨叶表面压力分布加载于桨叶上，通过计算，可以直观地看到桨叶的变形云图。图14～图16给出了迭代稳定后的最大位移情况：最大变形量在叶梢处，且随着侧斜角的增加，桨叶最大变形量不断增大；当侧斜为0°时，DTMB 4381的最大位移量为0.281 mm，侧斜为36°时，DTMB 4382的最大位移量为0.323 mm，侧斜为72°时，DTMB 4383的最大位移量为0.479 mm，可以看出DTMB 4382桨的最大位移量与无侧斜的DTMB 4381的较为接近，而侧斜为72°的DTMB 4383的增大较为明显。

图14 DTMB 4381桨桨叶变形分布图Fig.14 Deformation contours of DTMB 4381

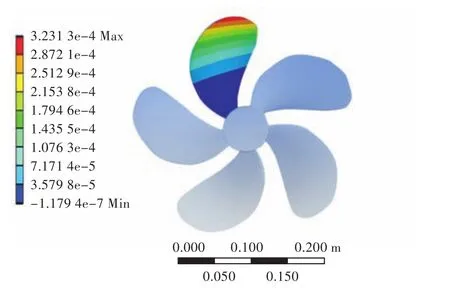
图15 DTMB 4382桨桨叶变形分布图Fig.15 Deformation contours of DTMB 4382

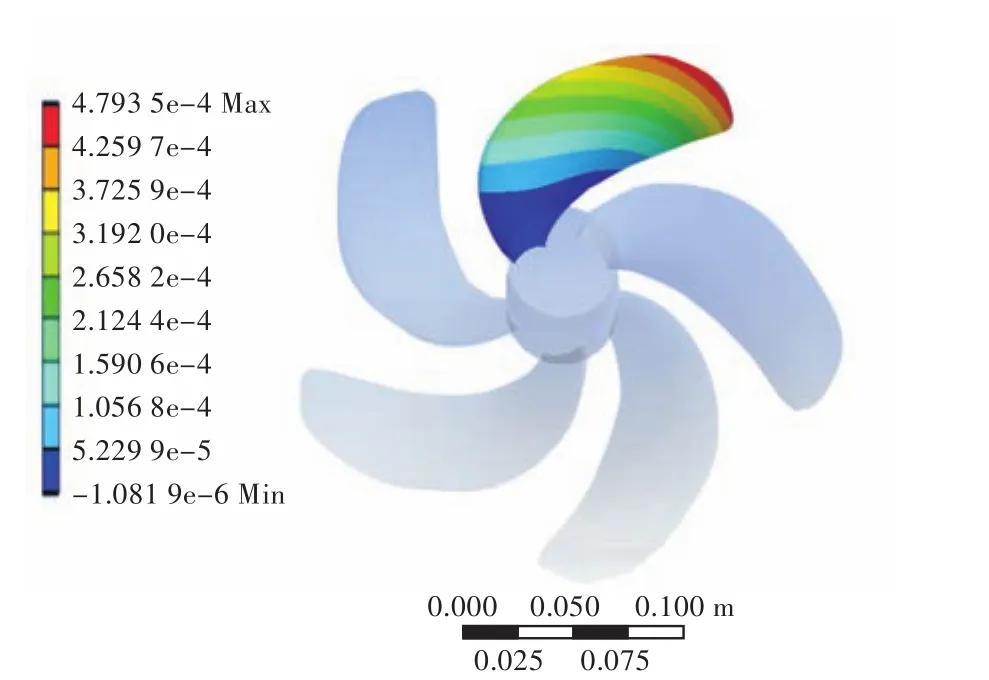
图16 DTMB 4383桨桨叶变形分布图Fig.16 Deformation contours of DTMB 4383

3.4 螺旋桨桨叶振动

计算采用单向瞬态耦合，整理得到桨叶最大位移随时间变化的曲线，然后，将单桨叶推力曲线的轮廓加入该曲线进行对比，如图17～图19所示。

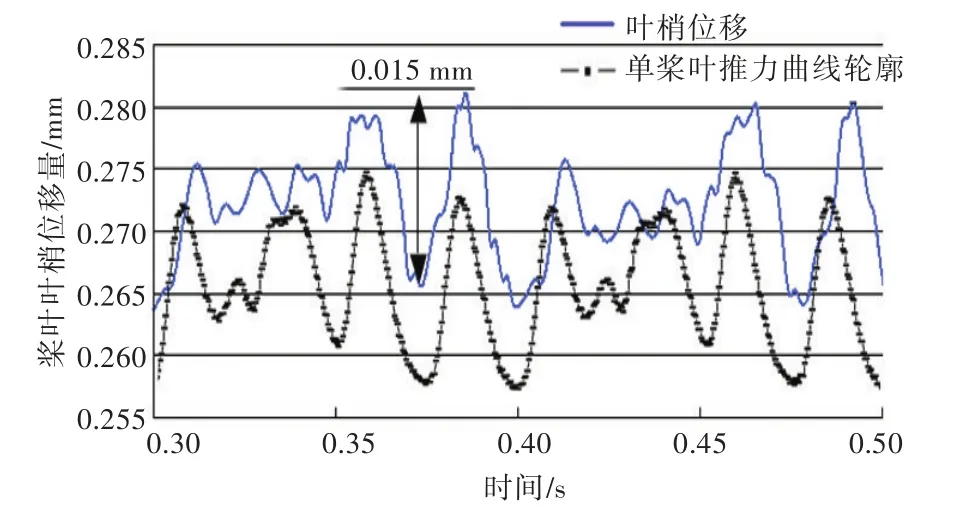
图17 DTMB 4381桨叶位移曲线Fig.17 The displacement curves of DTMB 4381

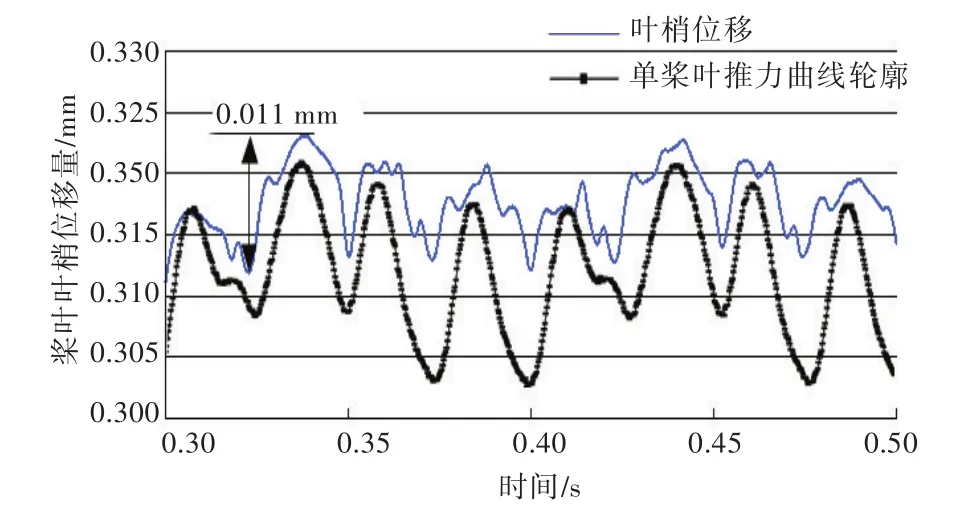
图18 DTMB 4382桨叶位移曲线Fig.18 The displacement curves of DTMB 4382

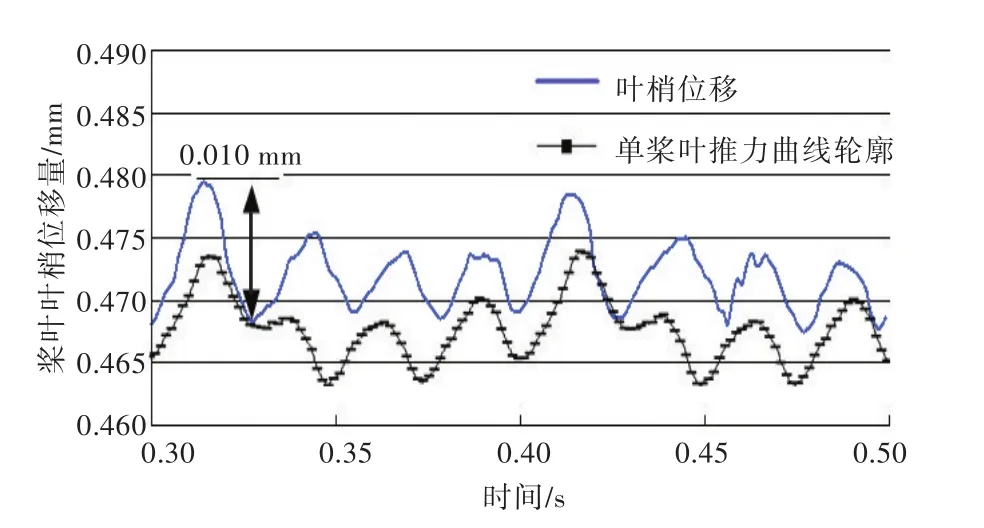
图19 DTMB 4383桨叶位移曲线Fig.19 The displacement curves of DTMB 4383

通过对比图17～图19可以看出，螺旋桨DTMB 4381的变形峰值为0.015 mm，为时均值的5.49%；螺旋桨DTMB 4382的变形峰值为0.011 mm，为时均值的3.47%；螺旋桨DTMB 4383的变形峰值为0.010 mm，为其时均值的2.12%；随着侧斜的增加，桨叶最大变形量随之增加，但变形曲线振荡会减弱。

图20～图22所示为桨叶振动加速度曲线及其频谱响应分析图。通过对比可以清晰地看到，随着侧斜的增加，桨叶振动幅值明显减弱，桨叶振动减弱的原因主要有2点：一是单个桨叶表面压力振荡减弱；二是侧斜变化有效地抑制了桨叶的振动。给出了桨叶振动曲线的频谱特性，其峰值对应的频率主要为40和80 Hz，其主要原因是十字形尾翼将来流分成了4个高、低速伴流区，桨叶旋转一周会交替进入4组高、低伴流区，从而使其具有4/T=40 Hz频率的非定常力特性，而这种非定常力加载于桨叶表面会引起桨叶变形振动频率同样接近于40 Hz；此外，桨叶振动加速度与桨叶表面的加载并不完全一致，在对应的二倍频、三倍频甚至是四倍频处都会产生振动。另外，还可以注意到有更小的幅值，其原因可能受指挥室围壳的影响，致使十字形尾翼分割成的4组高、低伴流不完全对称，或者不同周期内的数值计算结果有一定的差异。

图20 DTMB 4381单个桨叶振动加速度时域图与频谱分析图Fig.20 Time history curves of vibration acceleration and the Fourier transform of the blade of DTMB 4381

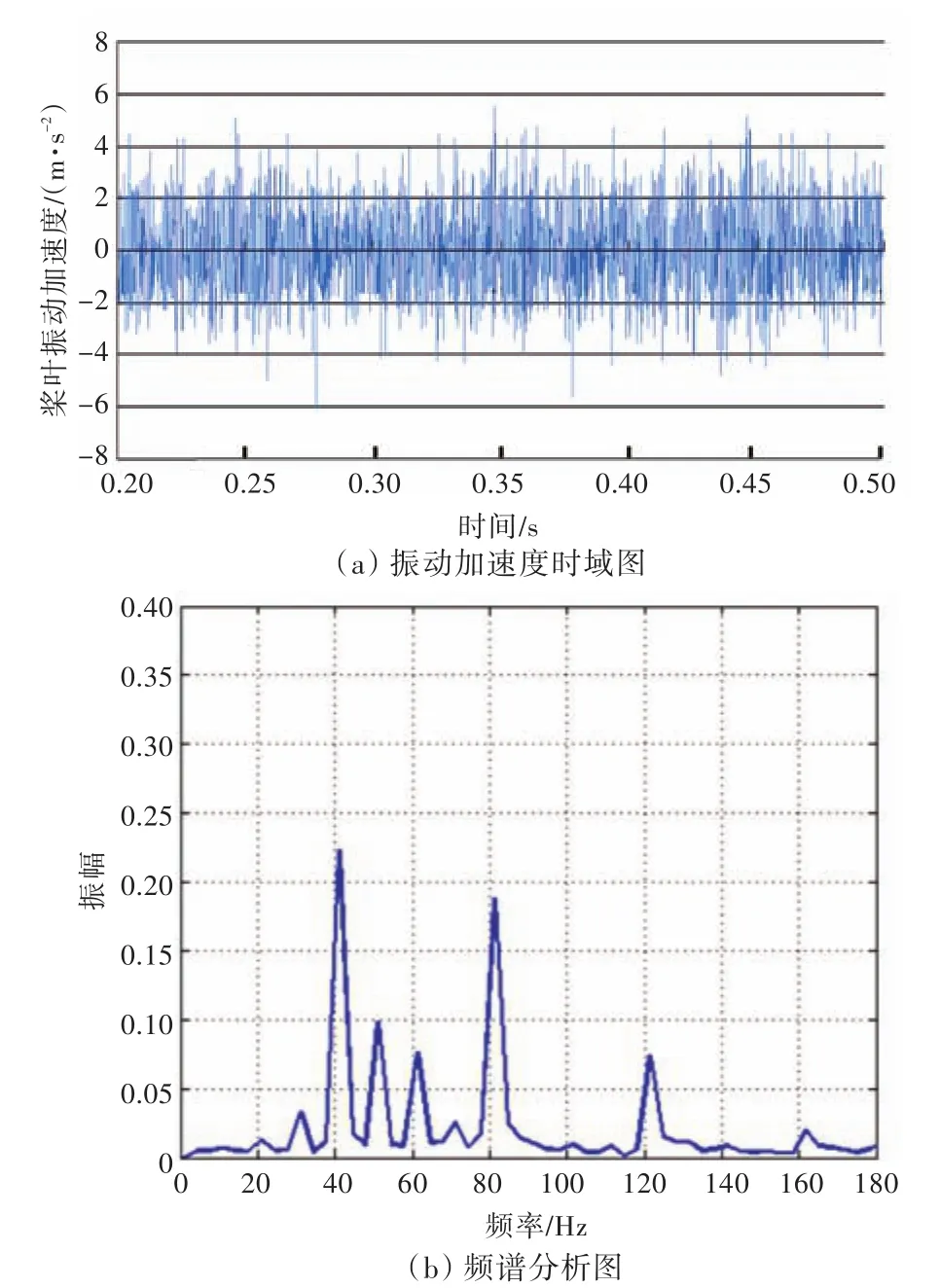
图21 DTMB 4382单个桨叶振动加速度时域图与频谱分析图Fig.21 Time history curves of vibration acceleration and the Fourier transform of the blade of DTMB 4382

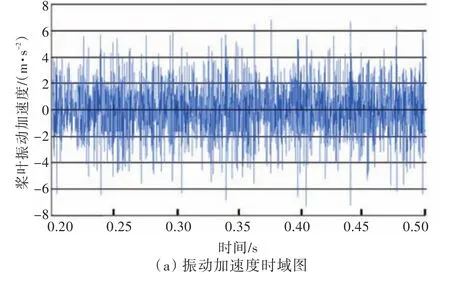
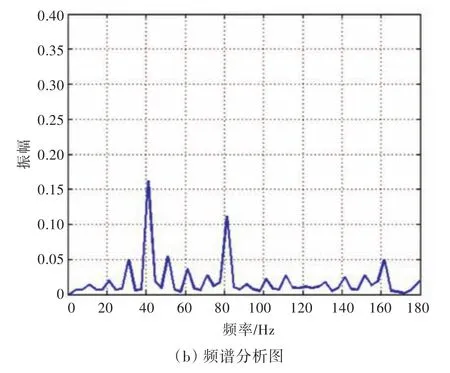
图22 DTMB 4383单个桨叶振动加速度时域图与频谱分析图Fig.22 Time history curves of vibration acceleration and the Fourier transform of the blade of DTMB 4383

4 结 论

本文以螺旋桨DTMB 4381，DTMB 4382和DTMB 4383为研究对象，利用ANSYS中流体载荷与结构响应数据的单向瞬态耦合技术FSI，实现将Fluent结果直接导入结构响应中进行瞬态计算，从而得到艇后螺旋桨的桨叶变形以及桨叶振动曲线。通过对不同侧斜螺旋桨的水动力性能、桨叶变形以及桨叶振动曲线进行数值模拟，得到以下结论：

1）首先，对螺旋桨的敞水性能进行仿真，通过对比敞水试验结果，确认了数值计算结果与试验值之间的误差以及数值模拟的可靠性与准确性；然后，通过对Suboff潜艇模型尾部不同侧斜螺旋桨非定常水动力性能进行数值仿真，分析了其推力、单桨叶推力随时间变化的规律，同时还对比了推力变化曲线与桨叶在不同位置时的伴流分布，获得了推力峰值与伴流峰值之间的对应关系，验证了推力变化规律与螺旋桨一阶叶频相关的一般性结论；最后，分析了侧斜对螺旋桨水动力的影响，发现随着侧斜的增加，螺旋桨激振力震荡明显减弱，为后续桨叶变形振动的流固耦合计算做好了准备。

2）对铜合金的螺旋桨进行流固耦合计算，得到了不同侧斜螺旋桨的桨叶变形及振动。桨叶变形会改变螺旋桨的几何初始参数，导致螺旋桨的侧斜有所增加，且侧斜越大，桨叶变形量越大，侧斜增加得越多，其抵抗变形的能力越弱；但当侧斜较大时，变形曲线的震荡会减弱，桨叶振动加速度幅值也会明显减弱，这表明随着侧斜的增加，在桨叶抵抗变形能力减弱的同时，抵抗变形波动以及侧斜波动的能力均有所增强。桨叶振动频率并不受侧斜影响，而是由艇后伴流场所决定。

［1］ GEORGIEV D J，IKEHATA H.Hydroelastic effects on propeller blades in steady flow［J］.Journal of the Society of Naval Architects of Japan，1998，184：1-14.

［2］ YOUNG Y L.Time-dependent hydroelastic analysis of cavitating propulsors［J］.Journal of Fluids and Struc⁃tures，2007，23（2）：269-295.

［3］ LIN H J，LIN J J.Nonlinear hydroelastic behavior of propellers using a finite-element method and lifting surface theory［J］.Journal of Marine Science and Tech⁃nology，1996，1（2）：114-124.

［4］ 孙海涛，熊鹰.桨叶变形对复合材料桨水动力性能影响［J］.华中科技大学学报（自然科学版），2013，41（6）：81-85. SUN Haitao，XIONG Ying.Effect of blade deformation of a composite propeller on its hydrodynamic perfor⁃mance［J］.Journal of Huazhong University of Science and Technology（Natural Science Edition），2013，41（6）：81-85.

［5］ 孙海涛，熊鹰.考虑变形的螺旋桨水动力及变形特性研究［J］.哈尔滨工程大学学报，2013，34（9）：1108-1112. SUN Haitao，XIONG Ying.Study on hydrodynamic and deformation performance of propellers considering the blade deformation［J］.Journal of Harbin Engineering University，2013，34（9）：1108-1112.

［6］ 孙海涛，熊鹰，时立攀.螺旋桨流固耦合特性的数值模拟［J］.江苏大学学报（自然科学版），2015，36（1）：23-29. SUN Haitao，XIONG Ying，SHI Lipan.Numerical simu⁃lation of fluid-structure interaction characteristics for propeller［J］.Journal of Jiangsu University（Natural Science Edition），2015，36（1）：23-29.

［7］ 孙海涛，熊鹰，黄政.大侧斜螺旋桨水动力及变形特性研究［C］//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会.北京：中国海洋出版社，2012：961-967.

［8］ 洪毅，赫晓东.复合材料船用螺旋桨设计与CFD/ FEM计算［J］.哈尔滨工业大学学报，2010，42（3）：404-408. HONG Yi，HE Xiaodong.Design of composite marine propeller and the calculation of CFD/FEM［J］.Journal of Harbin Institute of Technology，2010，42（3）：404-408.

［9］ 张帅，朱锡，侯海量.船舶螺旋桨流固耦合稳态求解算法［J］.哈尔滨工程大学学报，2012，33（5）：615-621.ZHANG Shuai，ZHU Xi，HOU Hailiang.Computation algorithm of fluid-structure interaction of marine pro⁃pellers in steady state［J］.Journal of Harbin Engineer⁃ing University，2012，33（5）：615-621.

［10］ 张帅，朱锡，周振龙，等.易变形船舶螺旋桨流固耦合特性分析［J］.海军工程大学学报，2014，26（1）：48-53. ZHANG Shuai，ZHU Xi，ZHOU Zhenlong，et al.Flu⁃id-structure interaction characteristics for flexible ma⁃rine propellers［J］.Journal of Naval University of En⁃gineering，2014，26（1）：48-53.

［11］ 吴建岚，周振龙.流固耦合下的复合材料螺旋桨变形特性研究［J］.船海工程，2013，42（6）：74-77. WU Jianlan，ZHOU Zhenlong.Study on deformation behaviour of composite propeller in FSI［J］.Ship& Ocean Engineering，2013，42（6）：74-77.

［12］ 熊鹰.非均匀流中螺旋桨空泡及脉动压力的数值和实验研究［D］.武汉：武汉理工大学，2002. XIONG Ying.Numerical and experiment research on propeller-induced pressure fluctuations and cavita⁃tion in non-uniform flow［D］.Wuhan：Wuhan Univer⁃sity of Technology，2002.

［13］ LIEFVENDAHL M，TROËNG C.Computation of cy⁃cle-to-cycle variation in blade load for a submarine propeller，using LES［C］//Proceedings of the Second International Symposium on Marine Propulsors SMP' 11.Hamburg，Germany，2011：199-206.

［责任编辑：卢圣芳］

Effects of blade skew on the hydrodynamic and deformation performance of propellers

ZHANG Rui，WANG Xianzhou，ZHANG Zhiguo，JIANG Weijian，TAO Zhu
School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

During the operation of submarine propellers,the fluid mechanical pressure load on the blades could result in a structural load on the component,which in turn causes deformation of the blade.In this pa⁃per,the structural response is analyzed with the finite element method,and the coupling simulation is ac⁃complished by using ACT_Transient FSI in ANSYS Workbench.The geometries of the propeller DTMB 4381～4383 are then taken as the research objects,where the deformation characteristic and hydrodynamic performance of these propellers are studied.The results show that the max blade displacement worsens with the increase of skew angles,and the vibration of the blade decreases simultaneously.

propeller；Fluid-Structure Interaction（FSI）；thrust pulsation；deformation performance

U661.1

A

10.3969/j.issn.1673-3185.2015.06.013

http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1026.028.html期刊网址：www.ship-research.com

张瑞，王先洲，张志国，等.侧斜变化对螺旋桨水动力及变形振动特性的影响［J］.中国舰船研究，2015，10（6）：87-94. ZHANG Rui，WANG Xianzhou，ZHANG Zhiguo，et al.Effects of blade skew on the hydrodynamic and deformation performanceofpropellers［J］.Chinese Journal of Ship Research，2015，10（6）：87-94.

2015-06-15 < class="emphasis_bold"> 网络出版时间：

时间：2015-11-10 10:26

张瑞，男，1990年生，硕士生。研究方向：舰船水动力。E-mail：hust_zhangrui@hust.edu.cn王先洲（通信作者），男，1975年生，博士，讲师。研究方向：舰船水动力。E-mail：wangxz@hust.edu.cn