无人水面艇航向航速协同控制方法

曹诗杰，曾凡明，陈于涛

海军工程大学动力工程学院，湖北武汉 430033

无人水面艇航向航速协同控制方法

曹诗杰，曾凡明，陈于涛

海军工程大学动力工程学院，湖北武汉 430033

针对无人水面艇（USV）在未知干扰环境下的自主运动控制问题，研究基于模糊自适应算法的USV航向、航速协同控制方法。设计以航向角偏差量和直线距离偏差量为输入量，以及以舵角偏转控制量和油门开度控制量为输出量的模糊控制算法，并通过以航向角偏差率为输入量及以控制周期为输出量的自适应控制，使系统响应外部环境的变化。以抵达目标点的时间和舵角变化次数的加权最小值作为优化目标函数，分析论域、控制周期等参数对控制效果的影响。优化分析的结果表明：此方法在不同海面风、浪、流随机干扰的条件下，均能使无人艇抵达目标点，实现点对点的自主航行。

无人水面艇；模糊算法；自适应控制；协同优化

0 引 言

无人水面艇（USV）是一种无人操作的水面舰艇，属于无人智能动力平台的研究领域。自主运动控制是USV区别于有人操纵船舶的核心技术之一。在自主运动的控制问题中，实用有效的航向、航速控制算法是USV平台在各种不确定水面环境中完成复杂航行任务的关键［1］。

目前USV航向、航速的控制方法主要包括以下2个方面。

1）将航向保持作为自动控制目标，使船舶能够自动跟随给定的航向，但是航向给定不在自主控制的范围内。相应的控制算法主要包括：基于精确运动模型的PID控制、Lyapunov控制、Back⁃stepping控制等常规控制算法［2］，基于在线辨识模型参数的变结构控制等自适应控制算法，基于模糊规则的模糊控制算法等［3］。

2）在航向保持的基础上，将航向给定纳入自主控制的范围，由艇载计算机通过控制算法自主得出航向给定值，进行闭环控制，但航速给定不包括在自主控制的范围内［4］。

以上控制方法存在的问题是：在控制算法方面，基于精确数学模型的常规控制算法中，船体运动模型较难精确确定，而且在不确定和强非线性的水面环境中，线性时不变的运动模型参数难以实时和准确地描述船体运动状态的变化；在自适应控制算法中，自适应函数和精确干扰模型较难确定；在模糊控制算法中，算法结构、输入输出变量的模糊域、模糊规则的确定需要丰富的工程实践经验；在控制策略方面，航向、航速的协同控制程度较弱，主要考虑航向对运动控制结果的贡献，仅将航向纳入自主控制算法的范围，而较少考虑航速对运动控制的快速性、鲁棒性和自主性的影响。

本文将针对现有技术的不足，研究一种基于模糊自适应算法的USV航向、航速协同控制方法，避免常规方法中的船体运动建模问题，改进模糊控制的策略和算法，融入自适应因素，提高控制方法在不确定水面环境中的适应性和鲁棒性。

1 航向、航速协同控制方法

1.1 试验研究平台

本文所搭建的USV试验研究平台如图1所示，表1为艇体主尺度。平台上所使用的航向、航速协同控制系统软、硬件包括：

1）艇载嵌入式计算机，用于综合处理数据信号和控制信号；

2）传感器模块，用于测量船体的位置、速度信息以及航向、航姿信息；

3）动力驱动模块，通过数/模转换输出电压信号，驱动航向、航速控制的执行机构；

4）自适应模糊控制器软件，用于将输入的数据通过模糊解算，得到输出的控制量的软件。

1.2 航向、航速协同控制模型

图1 USV试验研究平台Fig.1 Experimental research platform of unmanned surface vehicle

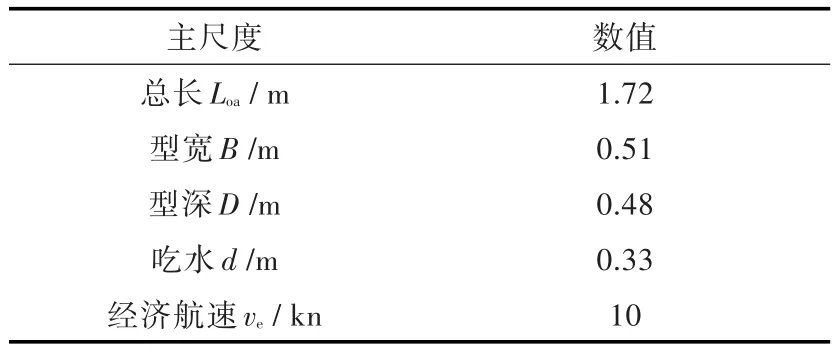
表1 USV艇体主尺度Tab.1 Main scale of the USV's hull

在现有的船舶运动控制研究中，一般研究船舶航向与航速控制的解耦问题，这在一定程度上解决了不匹配、不确定性的干扰。但要想得到更好的控制效果，就需要航向、航速协同控制，这将综合组成一个多输入多输出（MIMO）系统［5-6］。图2为本文的控制系统结构图。

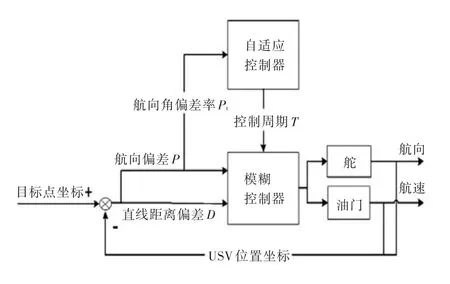
图2 控制系统结构图Fig.2 The structure figure of the control system

如图2所示，其控制原理是将USV与目标点比对得到的航向角偏差量P和直线距离偏差量D作为系统输入量，取代常规的模糊控制中航向角偏差量和航向角偏差率。因为本系统采用寻目标点的方法进行自主航行，在靠近目标点的过程中，距离偏差影响的控制效果更为明显［7-8］。系统的输出量设计为舵角偏转控制量U和油门开度控制量V这2个角度量，分别对应于对USV航向和航速的控制。

图3为本文所设计的USV航向、航速协同控制模型，同时也是试验平台软件的设计框架。具体控制方法分为2个子线程，分别对应模糊控制和自适应控制方法。

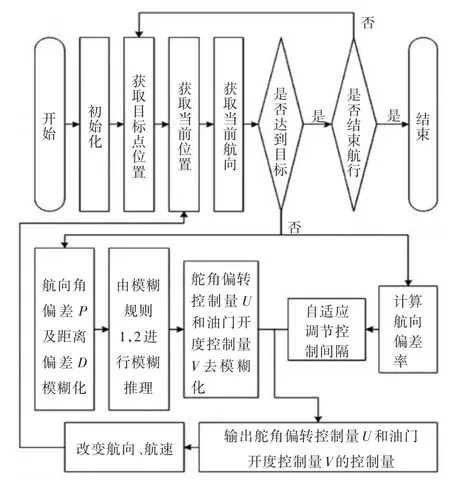
图3 航向、航速协同控制模型Fig.3 The model of the direction and speed cooperative control method

模糊控制线程中，对P和D进行模糊自适应控制算法的解算，由P和D在模糊集合中的隶属度计算，并输出U和V。

自适应控制线程中，计算单位时间航向角偏差率Pt=P/t，将航向角偏差率划分为3档，对高航向角偏差率使用较短的控制周期，反之，使用较长的控制周期，实现自适应调节模糊控制器参数，响应外部环境变化。

1.3 模糊自适应算法

本文所采用的模糊自适应算法是基于仿真实验和专家经验，拟定各函数参数和模糊规则［9-11］，并通过获取外界的环境变化采用应对机制进行一定的自适应调整。

首先，通过数据前处理得到算法的输入量。由传感器获取的位置及角度信息及初始设定可得到经度方向上的距离偏差量X（以东为正方向），纬度方向上的距离偏差量Y（以北为正方向），航向角θ（以真北方向为参考），由下式得到P和D：

将得到的P和D分别引入各自的隶属度函数进行模糊化处理，同样输出的U和V也分别由对应各自的模糊集合和隶属度函数表征。定义Aj为一个模糊集合

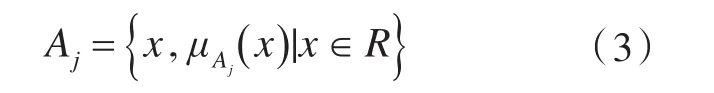
式中：A代表模糊量集合，以下由P，D，U，V具体指代，标识号j的不同值对应于不同的模糊分区；模糊集合的自变量是x，x的变化范围R为x的论域，代表其取值范围。本文中，对于P和U，j=-2，-1，0，1，2分别代表NB（负向大偏差/左舵大偏转），NS（负向小偏差/左舵小偏转），ZE（零偏差/零舵角），PS（正向小偏差/右舵小偏转），PB（正向大偏差/右舵大偏转），同样，对于D和V，j=0，1，2分别代表Z（零偏差/零油门），S（小偏差/小油门），B（大偏差/大油门）。对应不同的模糊集合，自变量有各自的高斯隶属度函数，其表达式为

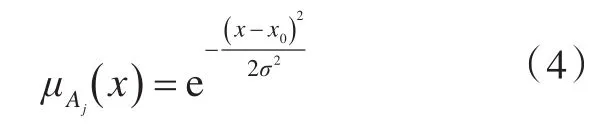
式中：x0决定了函数的中心位置；σ决定了函数的陡度。高斯函数法隶属度函数相对普通三角隶属度函数而言较为复杂，但是它能够很好地抵抗外界的不确定性干扰，同时，类似正态曲线的形式更符合未知环境这一随机概率事件［12-13］。输入输出量各自的隶属度函数曲线簇如图4所示。

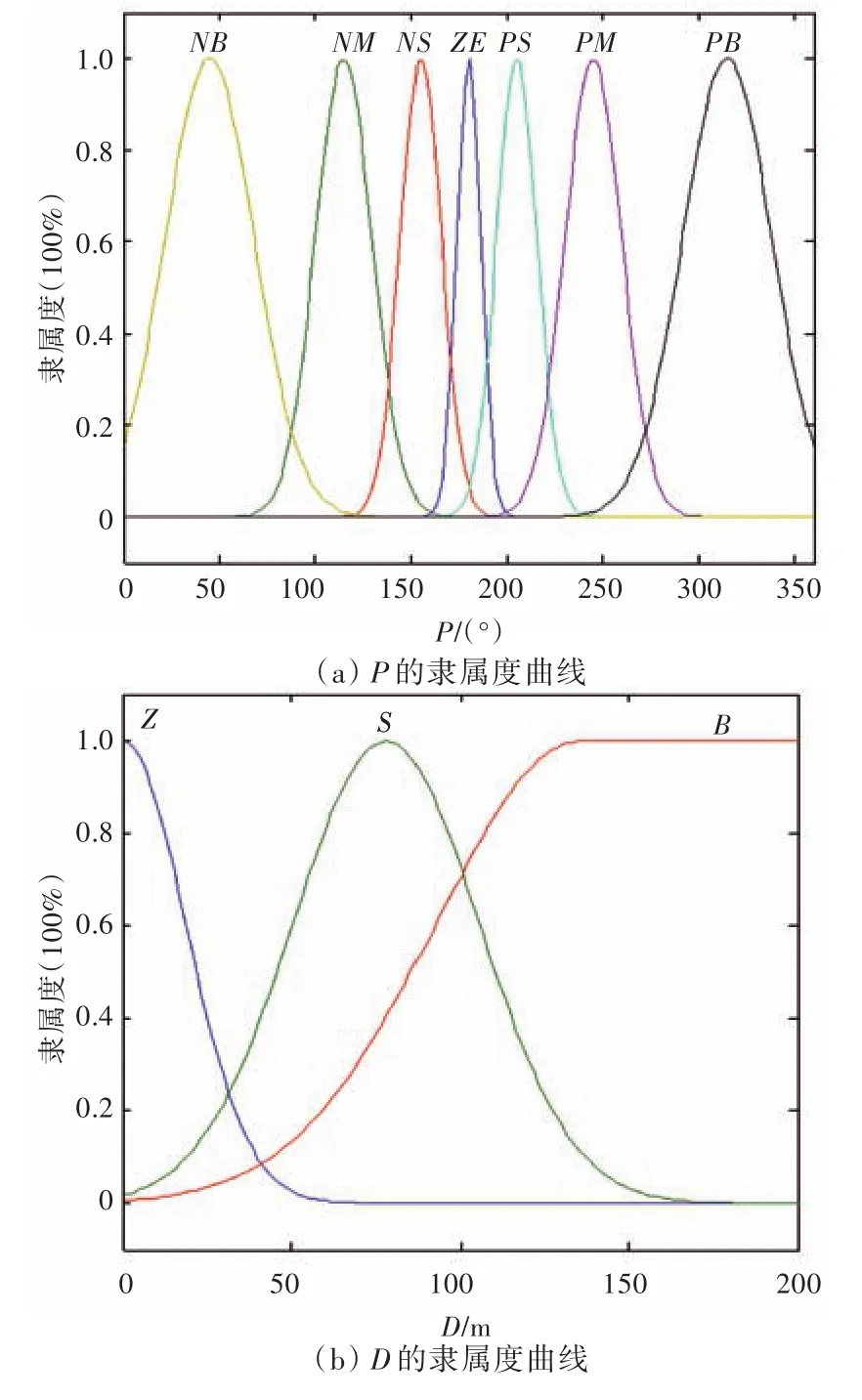
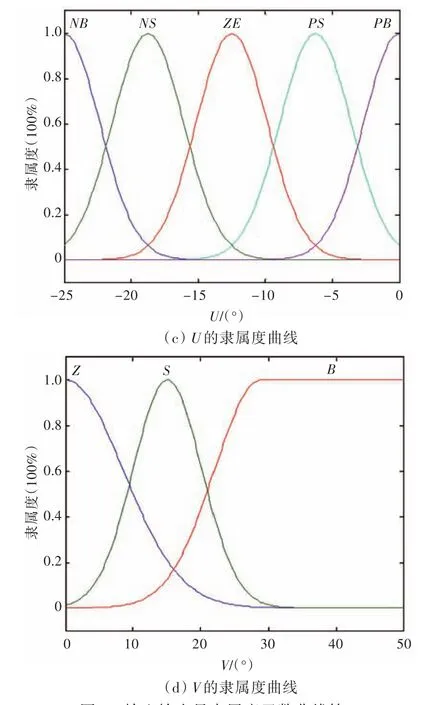
图4 输入输出量隶属度函数曲线簇Fig.4 Curves collection of membership function of the inputs and outputs

输入量P和D模糊化后，将分别由对应的模糊规则推理出输出量U和V，表2和表3为推理过程的规则表。

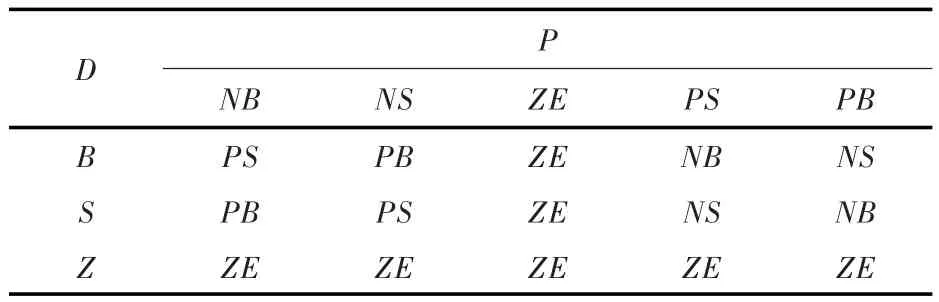
表2 舵角偏转控制量U模糊推理规则Tab.2 The fuzzy reasoning rule of deflection control of rudder angle U

表3 油门开度控制量V模糊推理规则Tab.3 The fuzzy reasoning rule of opening control of throttle V

模糊推理过程采用Mamdani规则，例如，为实现由输入量x∈P，y∈D得到输出量z∈U的推理过程，2条模糊控制规则语言为：

R1：IfxisP1 andyisD1 thenzisU1；

R2：IfxisP2 andyisD2 thenzisU2。

推理运算如下：

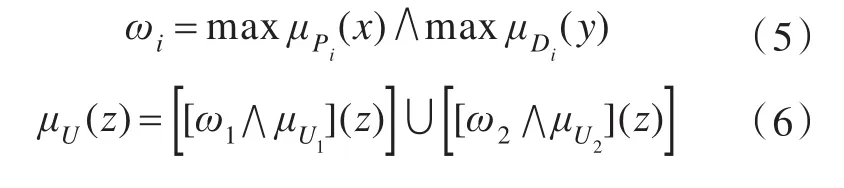
式中：符号∧指笛卡尔积，即进行取小运算的交集。中间变量ω为x和y在各自模糊集合中隶属度的最大值的取小结果。由此得到ω截取的输出量隶属度函数曲线的并集。最后对输出量清晰化，即曲线所围面积的形心坐标

在进入下一控制循环之前，引入自适应的方法调节自身参数可以提高算法的鲁棒性，加快对控制效果的收敛。本文中采用对控制周期进行自适应调节。计算Pt=P/t，将其按高低划分档位，代表控制环境的恶劣程度。在航向角偏差率较高时，视为复杂控制环境，采用高控制频率；在航向角偏差率较低时，视为平静控制环境，采用低控制频率；其余视为常规控制环境，采用经济巡航控制频率［14］。这样能够在海况复杂时提高控制效果，抗干扰能力强，在平静环境下增强计算精度和稳定性，延长使用时间。

本文所研究的控制算法与现有技术相比其优点在于：

1）采用模糊控制算法可以改善USV控制方法在不确定水面条件下的适应度，避免常规方法中船体运动的建模问题。

2）以经典模糊控制为基础，研究改进的2输入2输出USV模糊控制算法，增加距离模糊域函数作为算法输入，并将航向和航速都纳入自主控制范围，进行协同控制，提高USV运动控制的收敛速度，增强控制的鲁棒性。

3）采用航向角偏差率作为自变量，自动调节控制周期参数，使控制算法能够根据控制效果的变化，自适应地调整控制参数，进一步增强自主控制系统的智能性。

2 控制参数优化

在模糊自适应控制算法中，控制参数包括输入输出量论域、控制周期和模糊推理规则等，其中输入量论域和控制周期是影响控制效果的关键参数，可以进行量化分析寻优。

USV完成任务的过程中，抵达目标点时间和舵角变化的次数是任务完成的2个重要指标，将其加权作为目标函数，如下式所示

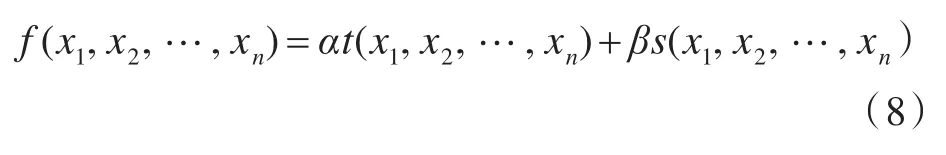
式中：t（x）为USV抵达目标的时间函数；s（x）为变舵次数函数，x为控制器参数；α，β分别为2个参数的权重，可以根据任务需求进行调整。以目标函数最小值为目标，即针对提高航行效率和减轻机构劳损进行参数寻优。

2.1 输入量论域优化分析

图5为输入量论域变化的USV航迹图，目标距离USV初始位置50 m，USV初始航向角90°，图中虚线圈为到达目标的范围圆，半径为5 m，设定USV到达圆中即视为到达目标。图中从左至右的航迹为输入量论域由小至大变化的结果。由于输入量论域中舵角偏差量隶属度函数的零偏差范围对控制效果的影响最为显著，零偏差的范围可视为对“正对目标”这个模糊概念定义的严格程度。

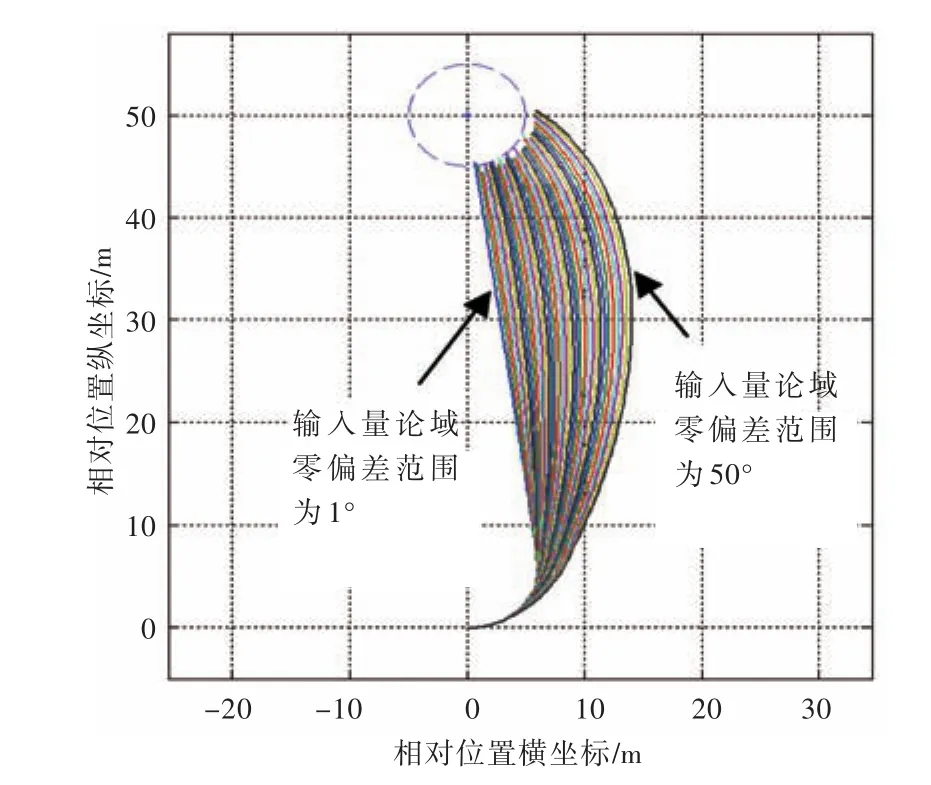
图5 输入量论域变化的USV航迹图Fig.5 The track figure of USV when the input's domain changes

图6和图7分别为抵达时间及变舵次数与输入量论域的关系，对仿真结果进行拟合，得到t（x）和s（x）的解析式。从图中可看出，抵达时间t与输入量论域正相关，变舵次数s与输入量论域负相关。将2个解析式代入式（8）中，f（x）取最小值时x的值即为输入量论域的最优解。

2.2 控制周期优化分析

图8为控制周期变化的USV航迹图，USV初始航向角为90°。图中从下至上的航迹为控制周期由小至大变化的结果。控制周期可视为“反应时间”这一模糊概念，可以从图中直观地发现，控制周期越长，USV朝目标点变化航向的响应越迟缓。

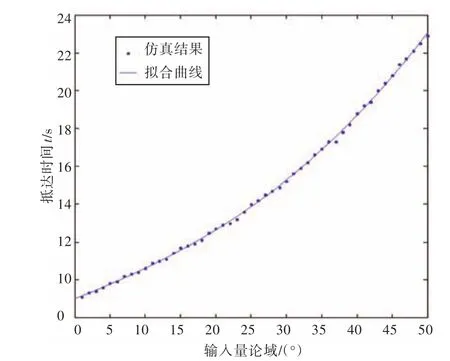
图6 输入量论域与抵达时间关系图Fig.6 The relationship between the arrival time and the input's domain

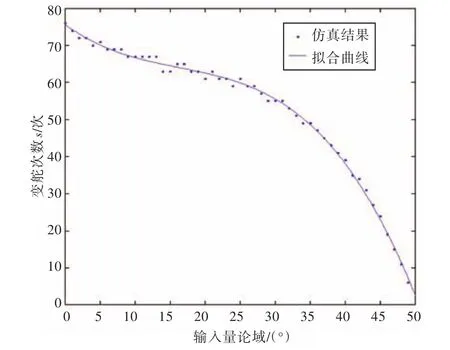
图7 输入量论域变化与变舵次数关系图Fig.7 The relationship between the change frequency of rudder and the input's domain

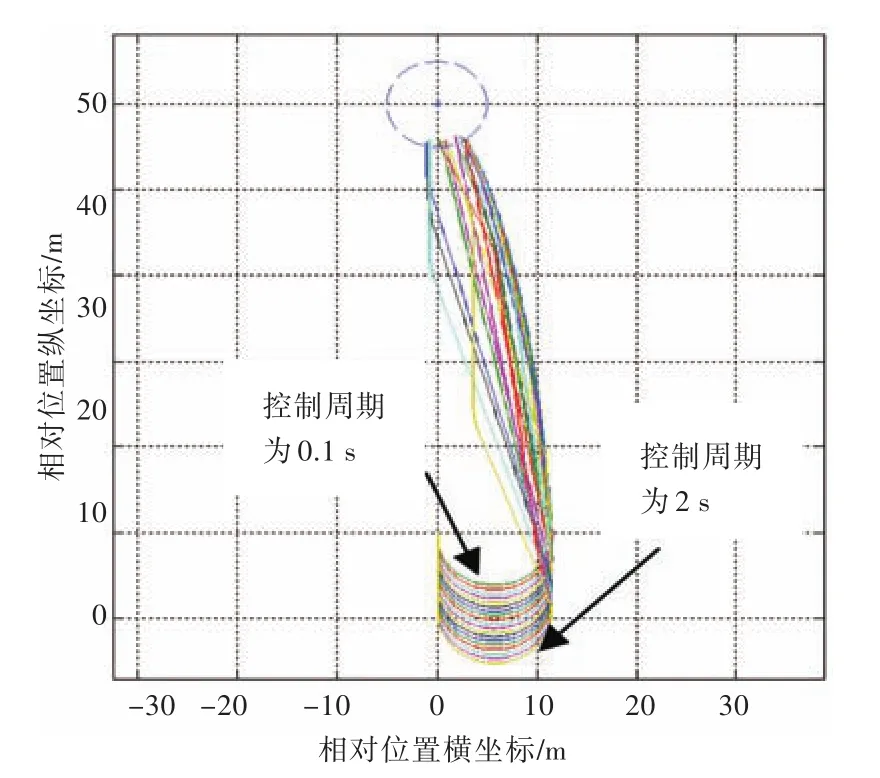
图8 控制周期变化的USV航迹图Fig.8 The track figure of USV when the control cycle changes

图9和图10分别为抵达时间及变舵次数与控制周期的关系，对仿真结果进行拟合，得到t（x）和s（x）的解析式，从图中关系曲线可知，抵达时间t与控制周期正相关，变舵次数s与控制周期负相关。但是在离散t（x）曲线中，曲线在高控制周期的波折较大，说明控制周期长则容错率较低，随机性加大，对环境鲁棒性不好，此时应该减少α的值，降低此指标的权重。同样将2个解析式代入式（8）中，f（x）取最小值时x的值即为控制周期的最优解。

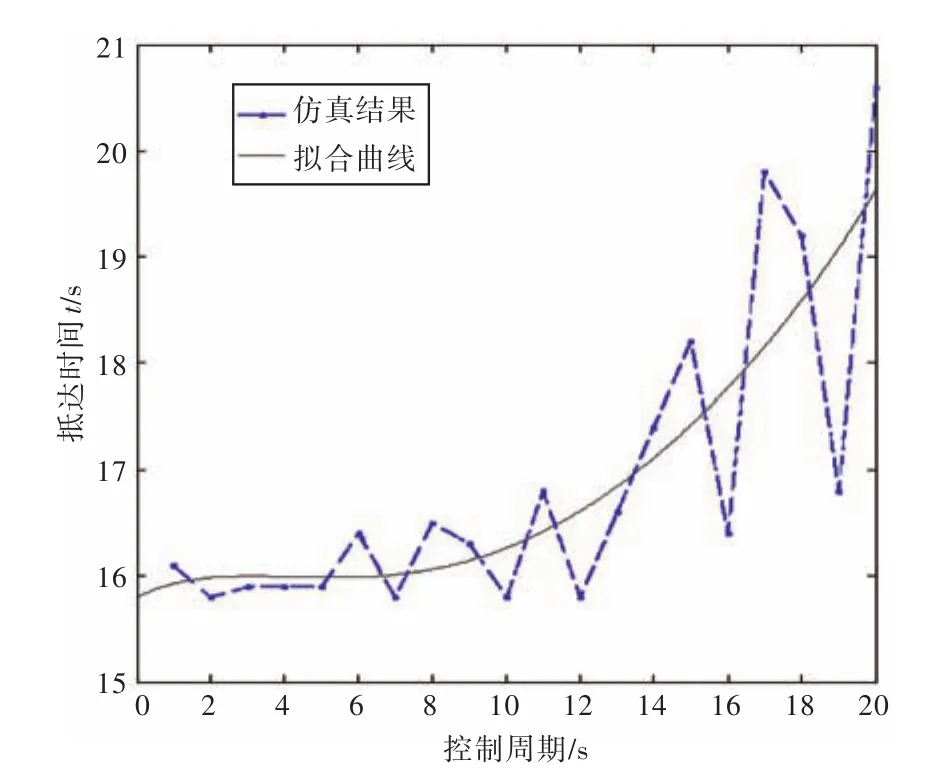
图9 控制周期变化与抵达时间关系图Fig.9 The relationship between the arrival time and the control cycle

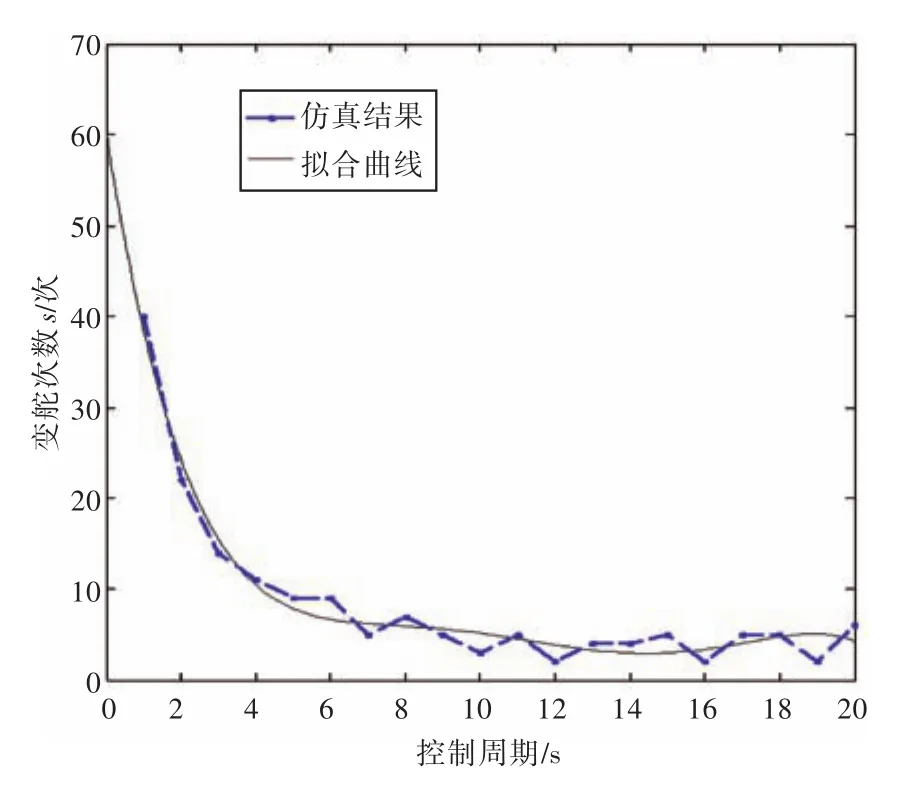
图10 控制周期变化与变舵次数关系图Fig.10 The relationship between the change frequency of rudder and the control cycle

控制参数优化分析的结果表明：

1）控制模型的性能参数是t和s，优化参数是输入量论域和控制周期，其中，t与输入量论域正相关，s与输入量论域负相关，t与控制周期正相关，s与控制周期负相关。

2）在关系曲线波动大，拟合曲线精度不高的情况下，应适当降低该关系函数的权重。

3）单一优化变量时，目标函数f（x）有界且收敛，能够求得最小值，说明优化方法普适于所有控制参数。由此可见，以上的优化方法能够切实有效地寻找到最优控制器参数。

2.3 优化效果分析

图11为USV在最优控制器参数的条件下，处于几种随机干扰情况的仿真结果航迹图。设定初始航向角为90°。

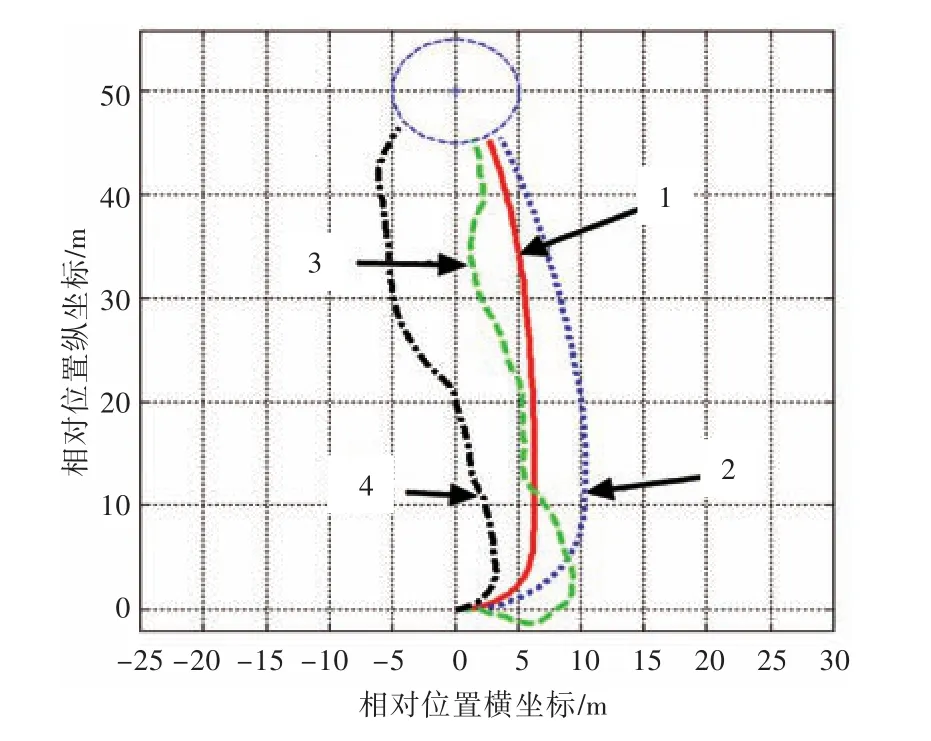
图11 不同随机干扰下的USV航迹图Fig.11 The track figures of USV under different random disturbances

考虑到USV工作环境的风、浪、流对控制效果的影响，仿真时用以下状态对航行时船舶受到的扰动进行模拟［15］：

1）平静水面，无扰动情况下的控制效果，结果如曲线1所示。

2）风或流对船舶的恒值扰动：ω=5°，结果如曲线2所示。

3）风、浪、流综合均匀随机干扰：ω=(4.5H1+ 3.5H2)°。H1和H2是2个相互独立的服从［0，1］均匀分布的伪随机变量，结果如曲线3所示。

4）风、浪、流综合正态分布随机干扰：ω=(4.5H3+3.5H4)°。H3和H4是2个相互独立的服从标准正态分布N（0，1）的伪随机变量，结果如曲线4所示。

由仿真结果可知，在随机扰动下，模糊自适应控制器能对系统输出进行有效的控制，实现了寻目标点自主航行，且USV在不同扰动下的抵达时间相对于平静航行增幅在10%以内。可以认为，该控制器能够有效适应外界环境，抗干扰强，稳定性好。

3 结 语

本文研究了一种USV航向、航速协同控制方法，利用模糊控制算法的优点，使用多输入多输出的控制结构，对航向、航速进行了协同控制。并且加入自适应控制环节，使系统能够对未知变化环境进行自主调节。通过试验平台的控制系统进行仿真及优化分析，得出了一套行之有效的优化方案，并对优化效果进行了抗干扰分析，为进一步的试验研究工作提供了理论基础。

［1］ YAN R J，PANG S，SUN H B，et al.Development and missions of unmanned surface vehicle［J］.Journal of Marine Science and Application，2010，9（4）：451-457.

［2］ DO K D.PAN J.Global robust adaptive path following of underactuated ships［J］.Automatica，2006，42（10）：1713-1722.

［3］ 陈铭.高速无人艇模型及航速/航向解耦控制研究［D］.哈尔滨：哈尔滨工程大学，2011.

［4］ 陈鸶鹭，程海边.基于模糊神经网络控制的水面无人艇建模与仿真［J］.舰船科学技术，2010，32（11）：134-136. CHEN Silu，CHENG Haibian.Modeling and simula⁃tion based on fuzzy neural network for unmanned sur⁃face vehicle［J］.Ship Science and Technology，2010，32（11）：134-136.

［5］ CACCIA M，BONO R，BRUZZONE G，et al.Design and exploitation of an autonomous surface vessel for the study of sea-air interactions［C］//Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Barcelona，Spain，2005：3582-3587.

［6］ CACCIA M，BONO R，BRUZZONE G，et al.An au⁃tonomous craft for the study of sea-air interactions［J］. IEEE Robotics and Automation Magazine，2005，12（3）：95-105.

［7］ 徐博，奔粤阳.自主水下航行器建模、控制设计与仿真［M］.北京：国防工业出版社，2013：117-138.

［8］ 伍文晖.水面无人艇试验平台设计［D］.大连：大连海事大学，2013.

［9］ LIAO Y L，WAN L，ZHUANG J Y.Backstepping dy⁃namical sliding mode control method for the path fol⁃lowing of the underactuated surface vessel［C］//Interna⁃tional Conference on Advanced in Control Engineering and Information Science.Amsterdam，2011.

［10］ CHWA D.Global tracking control of underactuated ships with input and velocity constraints using dynam⁃ic surface control method［J］.IEEE Transactions on ControlSystems Technology， 2011， 19（6） ：1357-1370.

［11］ DONG W.Cooperative control of underactuated sur⁃face vessels［J］.IET Control Theory and Applica⁃tions，2010，4（9）：1569-1580.

［12］ BØRHAUG E，PAVLOV A，PANTELEY E，et al. Straight line path following for formations of underac⁃tuated marine surface vessels［J］.IEEE Transactions on Control Systems Technology，2011，19（3）：493-506.

［13］ CONSOLINI L，TOSQUES M.A minimum phase out⁃put in the exact tracking problem for the nonminimum phase underactuated surface ship［J］.IEEE Transac⁃tionson Automatic Control，2012，57（12）：3174-3180.

［14］ JIA H M，ZHANG L J，BIAN X Q，et al.A nonlinear bottom-following controller for underactuated autono⁃mous underwater vehicles［J］.Journal of Central South University，2012，19（5）：1240-1248.

［15］ 孙巧梅.无人艇建模及逻辑网络自适应控制方法的研究［D］.大连：大连海事大学，2013.

［责任编辑：胡文莉］

The course and speed cooperative control method for unmanned surface vehicles

CAO Shijie，ZENG Fanming，CHEN Yutao
College of Power Engineering，Naval University of Engineering，Wuhan 430033，China

In order to solve the problem of autonomous dynamic control for unmanned surface vehicles (USV)under unknown conditions,a course and speed cooperative control method based on the adaptive fuzzy algorithm is studied in this paper.The fuzzy control algorithm is designed as to the inputs are the devi⁃ation of course and position,and the outputs are the rudder angle and throttle.The self-adaptive control method is applied,of which the input is the deviation rate of course and the output is the control cycle,to make the system effectively response to external changes.The objective function of the optimization is the weighted minimum of the arrival time and the changing frequency of rudder.The specific effects of the pa⁃rameters,like domains and the control cycle,are analyzed.The results of optimization analysis show that the method enables the USV to successfully reach the target point in random disturbance conditions with different wind,current and wave,and to achieve the point to point autonomous voyage.

Unmanned Surface Vehicle（USV）；fuzzy algorithm；self-adaptive control；cooperative opti⁃mization

U664.82

A

10.3969/j.issn.1673-3185.2015.06.011

http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1025.018.html期刊网址：www.ship-research.com

曹诗杰，曾凡明，陈于涛.无人水面艇航向航速协同控制方法［J］.中国舰船研究，2015，10（6）：74-80. CAO Shijie，ZENG Fanming，CHEN Yutao.The course and speed cooperative control method for unmanned surface vehicles［J］.Chinese Journal of Ship Research，2015，10（6）：74-80.

2015-05-05 < class="emphasis_bold"> 网络出版时间：

时间：2015-11-10 10:25

中国博士后科学基金资助项目（201150M1547）；湖北省自然科学基金资助项目（2013CFB440）

曹诗杰，男，1991年生，硕士生。研究方向：舰船动力装置总体设计、分析与优化。E-mail：975526435@qq.com曾凡明（通信作者），男，1962年生，博士，教授，博士生导师。研究方向：舰船动力装置总体设计、分析与优化