悬链线构件的有限元方法

王瀚，解德，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2船舶与海洋水动力湖北省重点实验室，湖北武汉430074

3高新船舶与深海开发装备协同创新中心，上海200240

悬链线构件的有限元方法

王瀚1，解德1，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2船舶与海洋水动力湖北省重点实验室，湖北武汉430074

3高新船舶与深海开发装备协同创新中心，上海200240

悬链线构件在船舶与海洋工程中是广泛存在的一种结构，无论是船舶码头旁靠、锚泊定位中的系泊线，还是各种系泊结构物中各种深海悬链线结构（如深海柔性立管、深海锚泊系统、复合材料悬链线立管等）的系泊力响应，对整个结构物都显得非常重要。其中，由于悬链线构件具有很强的几何非线性，其受力分析的精度对其运动响应的分析尤为重要。根据悬链线构件静力分析，得到悬链线单元的柔度矩阵，从而进一步推导出悬链线单元的刚度矩阵和单元节点力向量，最后以商业有限元软件ABAQUS的用户自定义单元（UEL）为工具，开发出悬链线单元。结果显示：运用此单元得到的简单悬链线结构的数值解与解析解完全一致，同时也基本符合实验结果，为解决各种复杂悬链线构件问题的直接计算法提供了一种新的思路。

系泊系统；悬链线单元；几何非线性；实验验证

0 引 言

21世纪是海洋的世纪，海洋中蕴含了大量的资源，如今海洋开发正在向深海发展［1］。仅就石油资源而言，目前进行的海洋石油开发主要模式为采用浮式或者固定式的各种适用于深海开发的新型海上石油生产处理装置。其中主要包括半潜式平台、张力腿平台（TLP）、单柱式平台（Spar）和浮式生产储油轮（FPSO）等系泊结构物。这些系泊结构物中的立管系统、锚泊系统等包含有大量的悬链线构件。对于立管系统而言，无论是传统的柔性立管、顶张力立管［2］，还是适用于高温、高压工作环境的钢悬链线立管［3-4］，亦或是结合上述各自优点还处于研究阶段的复合材料悬链线立管［5-6］，以及系泊结构物中进行海上定位的锚泊系统［7-11］，由于受风、浪、流等恶劣海洋环境的影响，它们要抵御外界的各种载荷以保证系泊结构物能正常工作运转。而对船舶而言，当进行码头旁靠或者水鼓系泊等各种停泊状态的分析时，悬链线构件都是重点关注的对象。因此，分析悬链线构件的受力无论是对海洋平台还是对船舶整个结构的运动响应都起着至关重要的作用。悬链线构件的受力主要表现为：在几何上为大变形，具有很强的几何非线性；悬链线的线长较大，其自重垂度不容忽略。针对悬链线的这些特点，必须选择正确的有限元模型对其进行非线性分析。Peuker等［12］将柔性管的每个组分都作为独立元素进行分析，并使其满足平衡条件和连续条件，建立了理论解析模型，但该模型无法计算立管的整体刚度值。Féret等［13］提出在柔性立管的总体分析中采用集中质量法，把柔性立管划分为有限数目的离散构件，将连续分布在柔性立管长度方向上的各种载荷等效集中在所建模型系统的节点处。对于锚泊系统而言，最常用的方法是采用包括非线性分析的通用有限元软件（如，ANSYS软件［14］）进行计算，然而软件的单元库中并不包含索单元。经过多年的发展，目前主要形成了3种主要数值模型［15］：用于静力分析的悬链线模型和用于动力分析的集中质量模型、细长杆模型。

本文将基于静力分析的悬链线模型推导出悬链线单元［16］，其可以根据一根索的任何一个参数值（如，索端张拉力或下垂高度）为已知条件来确定索的状态。并将进行相对应的实验［17］，用结果证明在商业有限元软件ABAQUS中运用该单元计算可以获得与解析解完全一致的结果，并且能与实验结果相吻合，以证明所推导出的单元的准确性。

1 悬链线的静力解析解

图1所示为无弹性悬链线段上任意一小段的静力图，其中W为系泊线单元长度的重量，dl为系泊线单位长度，T为系泊线的张力，dT为张力在dl上的增量，θ为张力T的方向与水平线的夹角，dθ为θ在dl上的增量。沿水平和垂直方向建立平衡方程，可以得到：

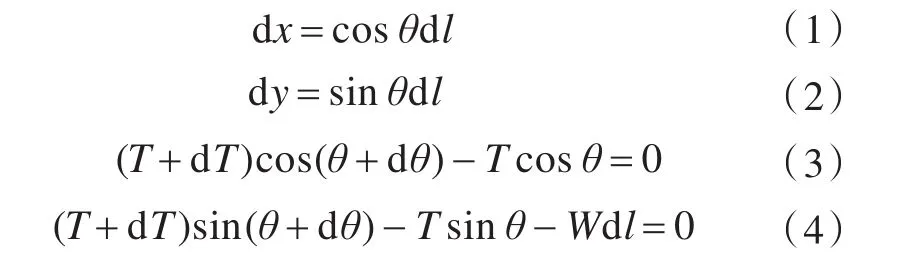
图2所示为无弹性悬链线段静力图。其中：Ta，θa与Tb，θb为悬链线段ab两端的张力及其倾角；T0为Ta和Tb的水平分量；ab长为l；a端和b端的垂直距离为y，水平距离为x。T0与Ta，Tb的关系如下：

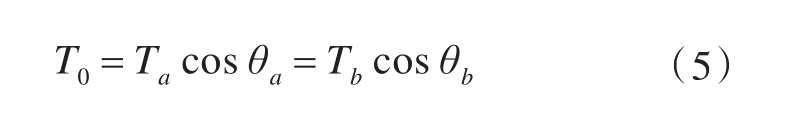
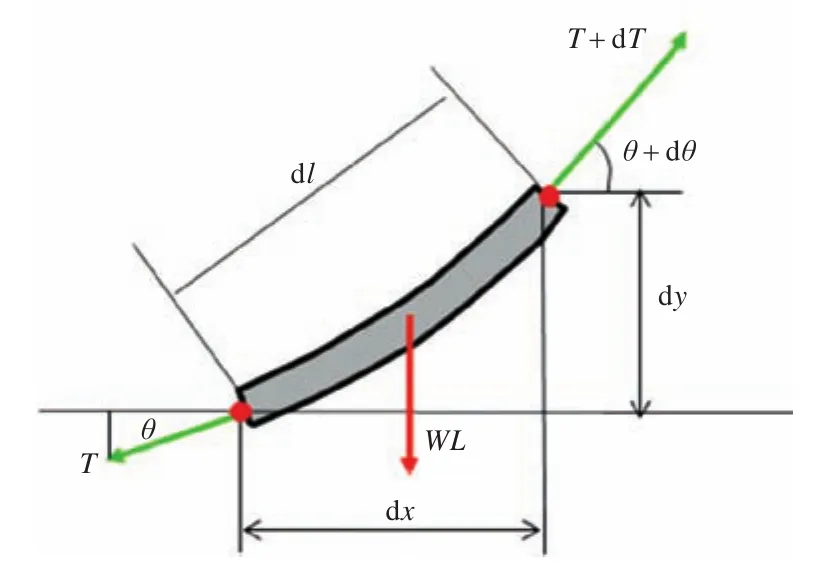
图1 无弹性悬链线静力图Fig.1 Statics graph of inelastic catenary

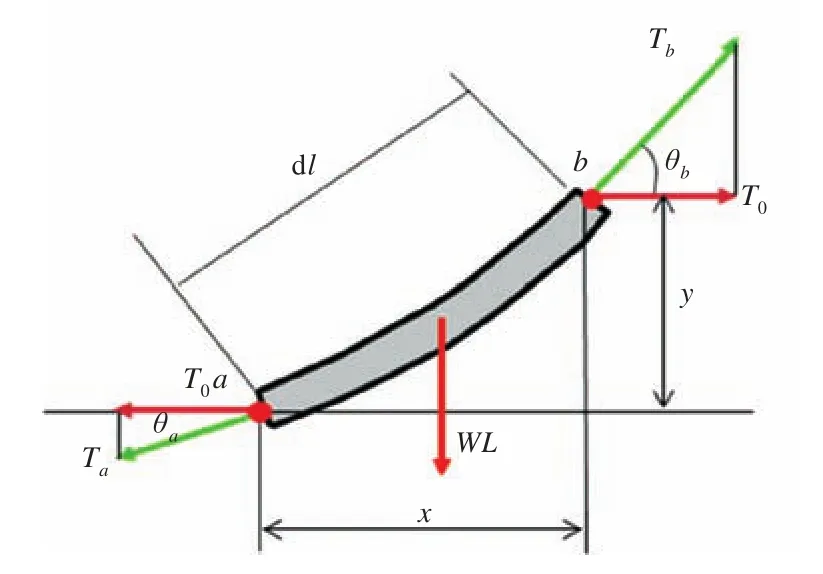
图2 无弹性悬链线单元静力图Fig.2 Statics graph of inelastic catenary element

由式（1）～式（5）可推导出悬链线段拉力的水平分量T0与其坐标的关系：

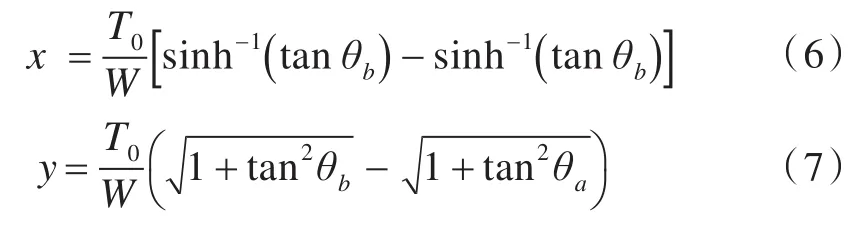
2 悬链线单元的刚度矩阵和节点力向量

将图2所示的悬链线段视为一个无弹性悬链线单元，如图3所示，由力的平衡条件，得

因此，式（6）和式（7）可改写为：

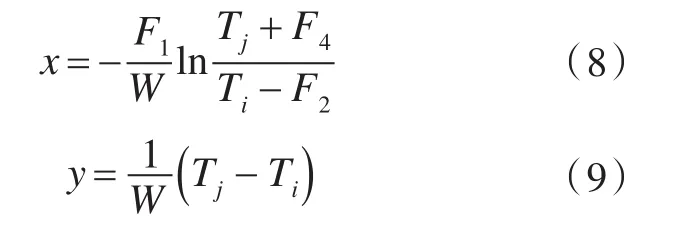
对式（8）和式（9）进行微分，得

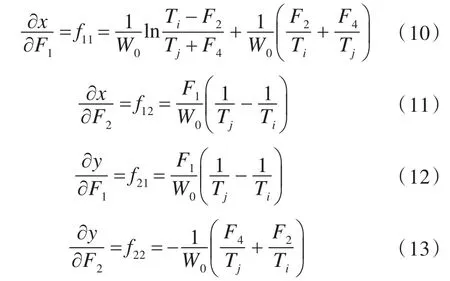
所以，可以得到

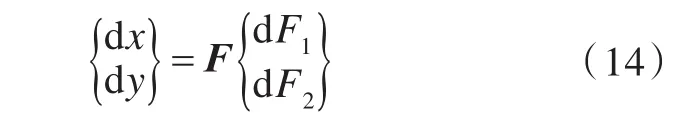
则刚度矩阵

式中，detF=f11f22-f12f21。

所以，单元的切线刚度矩阵为

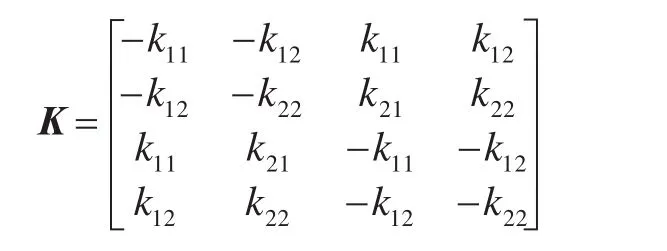
由于ABAQUS是一个通用的非线性有限元程序，因此它的求解过程是迭代法。因此结构的平衡方程为

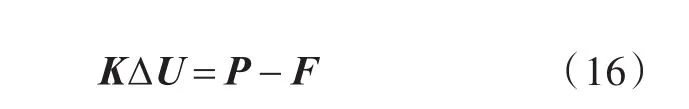
式中：ΔU为节点增量位移矩阵；P为各种外力形成的等效节点力矩阵。并以此为基础编写了二维问题的悬链线ABAQUS-UEL子程序。

3 悬链线单元的数值验证

以1根悬链线为例，链重W=100 kg/m，总长l=480 m。图4与图5分别为水深100 m和水深145 m时解析解与ABAQUS数值解的对比图。

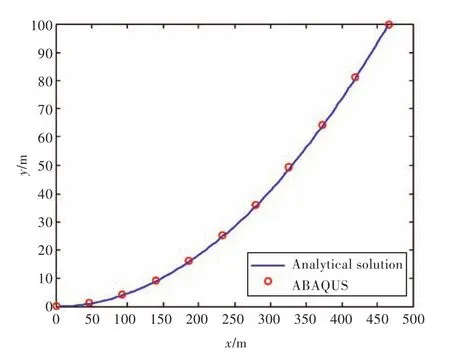
图4 水深100 m时结果对比Fig.4 The results contrast when depth is 100 m

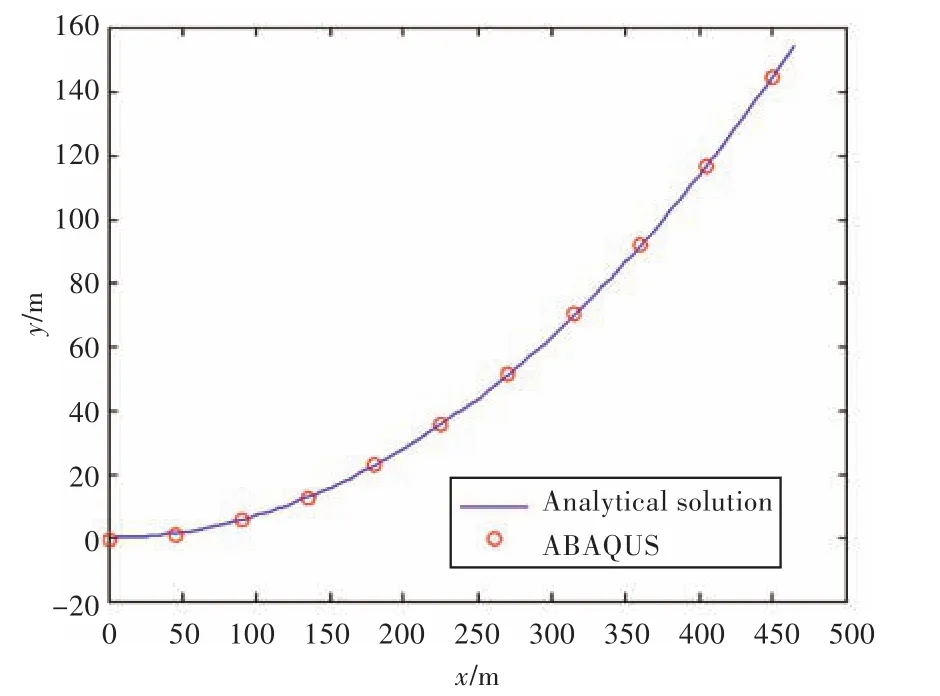
图5 水深145 m时结果对比Fig.5 The results contrast when depth is 145 m

可以看到，解析解与ABAQUS所求的数值解完全一致。

4 悬链线单元的实验验证

为进一步验证该单元的正确性，实验验证显然必不可少。铁链参数如下：

链重W/（N·mm-1） 0.002 844

总长l/mm 1 740

分别对500，1 000和1 500 mm这3个不同跨距下的悬链线进行了实验验证，与实验结果对比后的结果如图6～图8所示，图中带圆圈的线条为利用MATLAB得到的解析解。

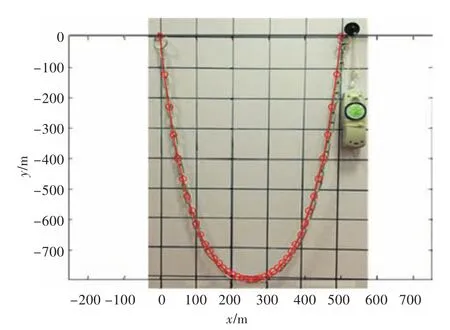
图6 跨距500 mm形状对比Fig.6 Shape comparison when span is 500 mm

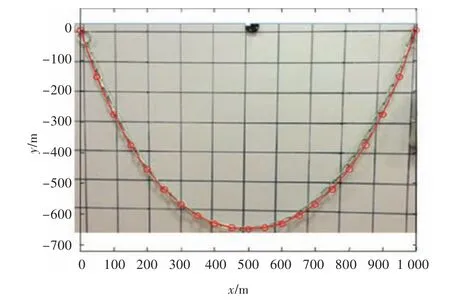
图7 跨距1 000 mm形状对比Fig.7 Shape comparison when span is 1 000 mm

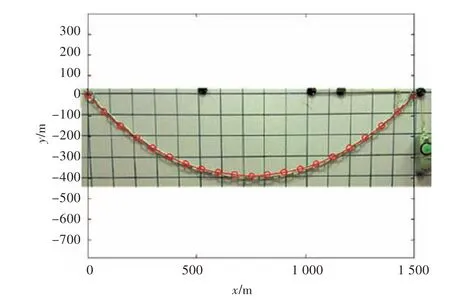
图8 跨距1 500 mm结果对比Fig.8 Shape comparison when span is 1 500 mm

利用测力计测得的最大拉力与解析解和数值解基本一致，具体结果如表1～表3所示。

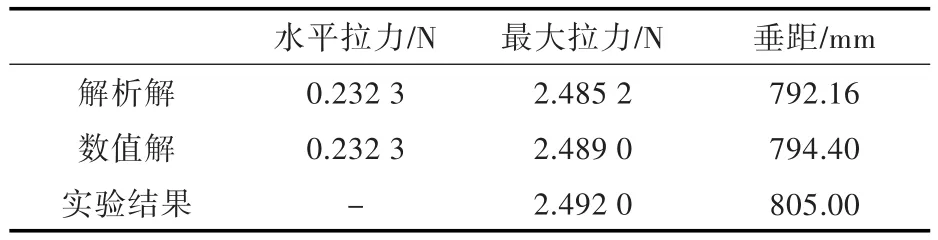
表1 跨距500 mm结果对比Tab.1 The results contrast when span is 500 mm

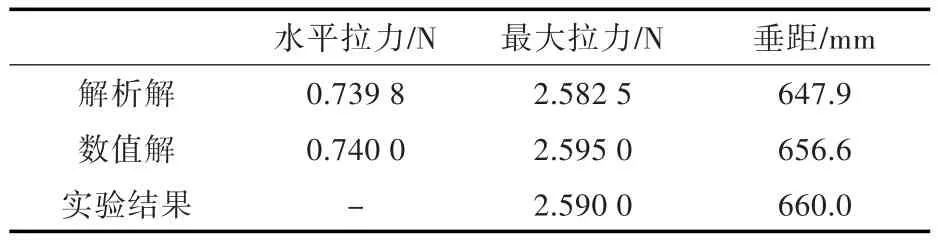
表2 跨距1 000 mm结果对比Tab.2 The results contrast when span is 1 000 mm

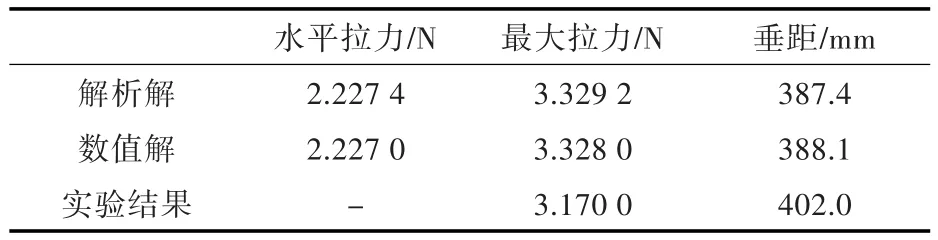
表3 跨距1 500 mm结果对比Tab.3 The results contrast when span is 1 500 mm

可以看到，利用MATLAB得到的解析解与实验中的铁链完全吻合，而通过测力计所得到的最大拉力以及链条的垂向距离也与解析解以及通过ABAQUS得到的数值解基本一致，从而进一步验证了此单元的精确度。

5 结 论

本文对悬链线构件的有限元分析进行了基础性的研究，并在简化模型中分析了其受力情况，主要结论如下：

1）计算出了悬链线的刚度矩阵，利用ABAQUS开发了一种悬链线单元，并且利用ABAQUS得到的数值解与解析解完全一致。

2）进行了简单的实验，并与解析解和数值解进行对比，结果基本吻合，证明了此悬链线单元的准确性。

3）本单元为解决悬链线构件运动等复杂问题的直接计算法提供了一种新的思路。但目前为止的计算及实验都是简化模型，还需对单元进行进一步的开发以使其能够适应多种载荷下以及在三维情况下的运动响应。

［1］ BAARHOLM R，PALAZZO F G.Hybrid verification of a DICAS moored FPSO［C］//Proceedings of the 14th International Offshore and Polar Engineering Confer⁃ence.Toulon，France：ISOPE，2004：307-314.

［2］ 姜豪，杨和振，刘昊.深海非粘结柔性立管简化模型数值分析及实验研究［J］.中国舰船研究，2013，8（1）：64-72. JIANG Hao，YANG Hezhen，LIU Hao.Experimental and numerical analysis of a new simplified model for the deepwater unbonded flexible risers［J］.Chinese Journal of Ship Research，2013，8（1）：64-72.

［3］ MARTINGS C A，HIGASHI E.A parametric analysis of steel catenary risers：fatigue behavior near the top［C］//Proceedings of the 10th International Offshore and Polar Engineering Conference.Seattle，USA：ISPOE，2000：54-59.

［4］ 黄维平，白兴兰，李华军.国外深水钢悬链线立管研究发展现状［J］.中国海洋大学学报，2009，39（2）：290-294. HUANG Weiping，BAI Xinglan，LI Huajun.State of the art of research and development of overseas deep⁃water steel catenary risers［J］.Periodical of Ocean Uni⁃versity of China，2009，39（2）：290-294.

［5］ OCHOA O O，SALAMA M M.Offshore composites：transition barriers to an enabling technology［J］.Com⁃posites Science and Technology，2005，65（15）：2588-2596.

［6］ 沈钦雄，杨和振，朱云.深海复合材料悬链线立管基于可靠度的优化设计［J］.中国舰船研究，2014，9（5）：77-84. SHEN Qinxiong，YANG Hezhen，ZHU Yun.Reliabili⁃ty-based design optimization of deep-water composite catenary risers［J］.Chinese Journal of Ship Research，2014，9（5）：77-84.

［7］ 陈徐均，崔维成，沈庆.对称式布置锚链系统的线性化处理［J］.海洋工程，2002，20（1）：75-79. CHEN Xujun，CUI Weicheng，SHEN Qing.Lineariza⁃tion for symmetrically collocated mooring system［J］. The Ocean Engineering，2002，20（1）：75-79.

［8］ 潘斌，高捷，陈小红，等.浮标系泊系统静力计算［J］.重庆交通学院学报，1997，16（1）：68-73. PAN Bin，GAO Jie，CHEN Xiaohong，et al.Static cal⁃culation of buoy mooring fast［J］.Journal of Chongqing Jiaotong Institute，1997，16（1）：68-73.

［9］ 胡灵斌，唐军.悬链线方程的求解及其应用［J］.船舶，2004（1）：17-20. HU Lingbin，TANG Jun.Solemnest and application of catenary's curve equation［J］.Ship and Boat，2004（1）：17-20.

［10］ 张火明，范菊，杨建民.复杂系泊系统静力特性快速计算方法研究［J］.舰船科学技术，2007，29（3）：113-118. ZHANG Huoming，FAN Ju，YANG Jianmin.Investi⁃gation on quick computation method of the static char⁃acteristics of complex mooring system［J］.Ship Sci⁃ence and Technology，2007，29（3）：113-118.

［11］ 郝春玲，滕斌.不均匀可拉伸单锚链系统的静力分析［J］.中国海洋平台，2003，18（4）：18-21，33. HAO Chunling，TENG Bin.Static analysis for a non-uniform flexible mooring cable system［J］.China Offshore Platform，2003，18（4）：18-21，33.

［12］ PEUKER M，KOKKINOWRACHOS K，GIESE K. Development of flexible riser for floating offshore pro⁃duction［C］//Offshore Technology Conference.Hous⁃ton，Texas：OTC，1987.

［13］ FÉRET J J，BOURNAZEL C L.Calculation of stress⁃es and slip in structural layers of unbounded flexible pipes［C］//Proceeding of First Offshore Mechanics and Arctic Engineering Specialty Symposium.New Orleans，Louisiana，1986：311-319.

［14］ 刘元丹，熊治国，刘敬喜，等.基于AQWA的旁靠油轮水动力相互作用研究［J］.舰船科学技术，2012，34（5）：13-17，22. LIU Yuandan，XIONG Zhiguo，LIU Jingxi，et al. Analysis on hydrodynamic interaction between side by side mooring tankers［J］.Ship Science and Tech⁃nology，2012，34（5）：13-17，22.

［15］ 王冰.基于细长杆理论的系泊缆索静力及动力分析方法研究［D］.哈尔滨：哈尔滨工程大学，2013.

［16］ 杨佑发，白文轩，郜建人.悬链线解答在斜拉锁数值分析中的应用［J］.重庆建筑大学学报，2007，29（6）：31-34. YANG Youfa，BAI Wenxuan，GAO Jianren.Applica⁃tion of catenary solution in numerical analysis of stayed cables［J］.Journal of Chongqing Jianzhu Uni⁃versity，2007，29（6）：31-34.

［17］ KIM M H，KOO B J，MERCIER R M，et al.Vessel/ mooring/riser coupled dynamic analysis of a tur⁃ret-moored FPSO compared with OTRC experiment［J］.Ocean Engineering， 2005， 32（14/15）：1780-1802.

［责任编辑：喻菁］

Analysis and experimetal verification of the catenary component with the finite element method

WANG Han1，XIE De1，2，3

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

2 Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics，Wuhan 430074，China

3 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China

The catenary component is widely applied on ships and ocean engineering structures.Whether it is for the mooring line of dockside ships,the anchor moored positioning,or various mooring structures with different deep-sea catenary structures(such as deep-sea flexible risers,deepwater mooring systems, deep-sea steel catenary risers,etc.),as well as the mooring force response of the entire structure are of par⁃ticular significance.To be more specific,the catenary component in the mooring system is obviously a non⁃linear structure geometrically,while the accuracy of the stress analysis of the catenary is particularly impor⁃tant.The stiffness matrix and node force vector of the catenary element can be gained based on the flexibili⁃ty matrix obtained from static analytical solutions of the catenary.Finally,the catenary element is estab⁃lished by using the UEL(User Defined Element)from commercial finite element software ABAQUS.The re⁃sult is seen to be fully consistent with the analytical solution and the experimental results.In brief,it induc⁃es creativity to the direct calculation method of solving various complex catenary component problems.

mooring system；catenary element；geometrical nonlinearity；experimental verification

U663

A

10.3969/j.issn.1673-3185.2015.06.006

http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1025.012.html期刊网址：www.ship-research.com

王瀚，解德.悬链线构件的有限元方法［J］.中国舰船研究，2015，10（6）：34-38. WANG Han，XIEDe.Analysisandexperimetalverificationofthecatenarycomponentwiththefiniteelementmethod［J］. Chinese Journal of Ship Research，2015，10（6）：.34-38

2015-03-18 < class="emphasis_bold"> 网络出版时间：

时间：2015-11-10 10:25

王瀚，男，1989年生，硕士生。研究方向：系泊结构物运动及响应。E-mail：327684188@qq.com解德（通信作者），男，1964年生，博士，教授，博士生导师。研究方向：船舶与海洋结构物设计制造