针对薄层介质的多极漫射模型扩展
吴一帆,杨旭波
(上海交通大学软件学院,上海200240)
针对薄层介质的多极漫射模型扩展
吴一帆,杨旭波
(上海交通大学软件学院,上海200240)
多极(Multipole)漫射模型能较准确地模拟半透明介质的次表面散射现象,但并不适用于厚度接近或小于一个平均自由程(MFP)的薄层介质。为此,在Multipole漫射模型的基础上扩展该模型使之适用于薄层介质。根据Multipole漫射模型所依赖的假设条件,针对薄层介质加以修改,将光线分解为直接透射和漫射部分,并调整Multipole放置点光源的方式,使之更符合薄层介质中光传输的特征。使用修改后的光源计算漫射部分,而直接透射部分则采用狄拉克δ分布来近似。对扩展方法和传统Multipole以及蒙特卡罗方法进行分布数值和实际渲染效果的对比,在处理厚度接近或小于一个MFP的薄层介质时,扩展方法的结果均较传统Multipole更吻合蒙特卡罗方法的结果,可直接和现有Multipole模型实现集成。
次表面散射;半透明;薄层介质;漫射模型;反射分布;平均自由程
1 概述
半透明介质在生活中无处不在:树叶、纸、蜡烛、牛奶、布料、生物的皮肤、贝壳、玛瑙等。事实上,几乎所有非金属物体都存在一定程度的次表面光传输现象[1]。如何正确地渲染这类物体是计算机图形学中的一个重要课题,而渲染它们需要首要解决的问题是如何模拟光线在半透明介质中的次表面散射现象。
在计算机图形学领域有不少针对半透明物体渲
染方法的研究。文献[2]提出了一个模拟光线在多层介质中的反射和折射的模型(H-K模型),使用蒙特卡罗方法模拟光线在各个表面上的反射、折射以及在介质中的散射、吸收现象。文献[3-4]针对皮肤扩展了H-K模型,增加了表面皮脂的模拟。文献[5]使用离散坐标模型给皮肤建模,考虑的是光线在2个粗糙表面之间半透明介质中的传播情况。这些模型均基于传统的双向反射分布函数,假设光线在物体表面的某一点入射,在同一点出射,并不能很好地描述次表面散射的一些特征,如阴影边缘处的颜色渗出现象。
本文提出一种基于Multipole模型的扩展方法,使得扩展后的Multipole模型适用于非常薄,即小于2个平均自由程(Mean Free Path,MFP)的介质。
2 背景介绍
直接求解辐射转移方程的方法可以非常准确地模拟次表面散射。这种完全基于蒙特卡罗(Monte-Carlo)方法的研究也有一些,比如文献[6-7]对湿润物体渲染的研究,文献[8]的研究。文献[9]提出了一个结合人体皮肤生物学特征的五层模型,通过蒙特卡罗方法模拟人体皮肤对特定波长光线的吸收、散射现象。所有这些方法的一个共同缺点是计算量太大,特别是对于以散射为主的介质(如皮肤),光线通常会在介质内部发生上千次散射才会离开介质或被吸收。
为了高效地模拟次表面散射的效果,计算机图形学领域出现了许多近似模型,大多数是基于双向散射表面反射分布函数(Bidirectional Scattering Surface Reflectance Distribution Function,BSSRDF)[10]的概念。文献[11]提出了Dipole漫射模型,使用漫射理论推导出BSSRDF的解析表达式。Dipole模型建立在介质无限厚以及均匀分布的假设上,对于具有一定厚度的介质以及多层介质并不适用。文献[12]使用Multipole模型替代了Dipole模型,给出了具有一定厚度介质的BSSRDF的解析表达式,同时使用Kubelka-Munk理论来计算多层介质的BSSRDF。文献[13]使用光子漫射,将Multipole方法扩展至不规则表面。这些模型的基本思路是将入射光转化为放置于一定位置的实光源和虚光源,其中实光源通常放置在表面以下一定距离的位置,这个距离通常和平均自由程(MFP)有关。这样的放置方法对于厚度小于这个固定距离的材料来说是病态的,通常会无法正确计算。文献[14]使用量化漫射部分解决了Multipole不适用于薄层介质的问题,但是他们使用的模型比Multipole复杂得多,并不容易与现有实现进行集成。
国内研究方面,目前较有代表性的是文献[15]关于皮肤渲染的论述,但也只是Multipole漫射模型的直接应用,未能涉及薄层介质的缺陷做相应改进。
3 Multipole漫射模型
3.1 双向散射表面反射分布函数
光线在半透明介质中的传播可以用双向散射表面反射分布函数(BSSRDF)表示[10]:

其中,L是出射辐射率;Φ是入射通量;xi和xo分别代表入射点和出射点的位置;ωi和ωo分别代表入射角和出射角。
文献[11]指出,针对均匀介质,考虑到径向对称性,BSSRDF可以用一个关于中心点距离的一维函数R(本文称为反射分布)以及菲涅尔(Fresnel)项表示:
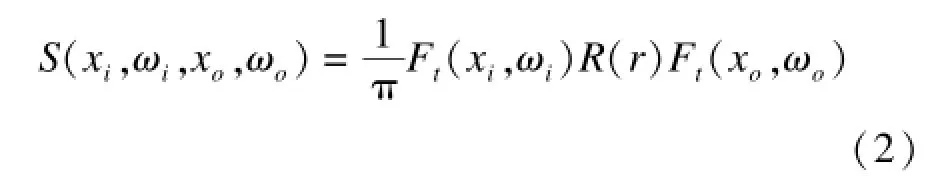
其中,r=xi-xo2为入射点和出射点间的距离;Ft(xi,ωi)和Ft(xo,ωo)分别表示入射点和出射点处的菲涅尔透射率。
3.2边界条件
漫射理论使用一个截断的球谐展开式来近似表示漫射辐射率:

其中,ϕ是标量辐照度;E是矢量辐照度。
记相对于表面的深度为z,z>0时为介质内部。对于介质表面,在平衡态时向下的漫射辐射率应该相当于向上的漫射辐射率在介质表面反射回内部的量,即:

其中,Ω+,Ω-分别表示对z>0,z<0部分积分;n为向外的表面法向量;Fdr=∫Ω+Fr(ω)(-n·ω)dω为内部菲涅尔漫反射系数,可用以下代数式来近似[17]:

其中,η为介质表面内外的相对折射系数。
将式(3)代入式(4),简化后即可得到边界条件:

对式(6)进行外插值,得到表面外距离zb=2AD处(z=-zb=-2AD处)辐照度为0。
对于厚度为d的介质,对下表面z=d重复上述过程可得到另一个边界条件[12]:

同样对式(7)外插值可以得到z=d+zb处辐照度为0。
Multipole漫射模型正是建立在式(6)、式(7)这2个边界条件之上,通过在表面上下放置一系列点光源,来达成这2个边界条件,从而计算径向反射率R和径向透射率T。
3.3 反射分布的推导

在2个点光源基础上,要满足边界条件式(7),可以将这2个点光源相对z=d+zb做一个镜像,得到一组新的点光源zr,1=2(d+2zb)+l,zv,1=2(d+ 2zb)-2zb-l。
这时边界条件式(6)不满足。继续将刚才的一组点光源相对z=-zb做一个镜像,得到新的一组点光源zr,-1=-2(d+2zb)+l,zv,-1=-2(d+2zb)-2zb-l。
依此类推,可以得到一系列的实点光源和虚点光源,它们的位置分别是:

其中,i=-n,-n+1,…n-1,n。
n趋近于无穷时,2个边界条件才同时被满足。图1(b)展示了部分点光源的位置。
将这些点光源在上下表面处(分别对应z=0和z=d)的贡献全部相加,得到反射分布和透射分布。

由于每一组点光源距离2个表面越来越远,它们对反射分布和透射分布的贡献也越来越小。实际计算时,取有限组点光源即可。本文的实现中使用11组(n=5)点光源来计算反射分布和透射分布。
从图1(c)中可以看到,实光源的放置位置对于厚度小于l的介质是病态的,因为这时实光源zr,0在介质之外,有相当一部分光线是直接透射而没有经历散射或吸收,这对于计算反射分布来说,会显著低估反射的量。在这种情况下,为了满足边界条件式(7),虚光源zv,1会过分接近介质上表面,从而降低其反射的量;同时,为了满足边界条件式(6),实光源zr,-1也会过分接近介质上表面,同样会降低反射量。对于透射分布来说,计算出的值有可能是负值。厚度稍大于l时,介质的下表面过于接近zr,0,可能会造成对透射量的高估。

图1 Multipole模型的点光源放置位置
3.4 多层材料
文献[12]提出Multipole漫射模型的同时也提供了处理多层材料的方法。在计算每一层的反射、
透射分布Ri,Ti后,根据Kubelka-Munk理论,对分布进行适当卷积即可得到多层材料的反射、透射分布:

其中,∗为卷积算子。
使用傅里叶变换将分布转换到频率域后,可以通过乘积操作快速计算。根据等比数列公式,有:

由于没有相应的解析表达式,本文的实现使用离散的方式计算各层的反射、透射分布,然后使用快速傅里叶变换转换到频率域进行操作,最后使用逆变换转换回离散分布。渲染时,使用线性插值对合并后的分布进行采样。
4 针对薄层介质的扩展方法

Multipole漫射模型的一个假设是大部分光线在介质中呈现漫射的性质,当介质厚度减少时,越来越多的光线会直接穿透介质而不发生任何散射或吸收,这种假设变得越来越不准确。考虑厚度d=0的极端情况,此时全部光线直接穿透介质,而没有任何反射,对应的反射和透射分布是:

其中,δ(r)表示中心在原点、径向对称的狄拉克δ分布函数,满足如下性质:

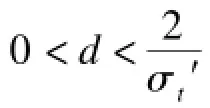

其中,i=-n,-n+1,…,n-1,n。
图2(b)展示了扩展后的点光源组放置情况。

图2 扩展方法中点光源的放置位置
结合两部分光线的贡献,可以得到扩展后的Multipole漫射模型:

其中,Rm,Tm为传统Multipole的反射、透射分布(式(9))。
剩下的问题就是如何选择H(d)。根据Lambert-Beer定律,一束光在介质中传播时其辐照度L与传播距离x有如下关系:
前期非洲猪瘟疫情防治工作取得的进展。主要是通过取缔泔水猪、限制生猪跨区域调运等途径,使得由餐厨剩余物喂猪引发的疫情由50%下降到34.3%,由生猪调运引发的疫情由35.3%下降到19.4%。

据此让H(d)大致等于发生漫射的光线相对于厚度为2MFP时的量:

最终的反射和透射分布可表示为:

4.2 狄拉克δ分布的离散表示方法
实现上可能的一个问题是如何表示狄拉克δ分布函数式(13)。离散分布P表示为相应的连续分布Pc在采样点处的值:

其中,s为采样步长;N为采样精度(决定离散分布P每行每列的元素个数)。离散卷积和连续卷积的关系如下:

其中,符号“~”表示“相当于”。由于本文使用离散分布进行计算,含有狄拉克δ分布的透射分布要与其他分布进行卷积操作,将δ(r)离散地表示为:


对于任意连续分布Pi,c及对应的离散分布Pi均成立。
如果预先对所有离散分布进行规范化,即令P′i=s2Pi,则离散分布之间的卷积操作便不涉及系数了,所有卷积操作完成后再进行反规范化即可。规范化后的狄拉克δ分布对应的离散分布如下:
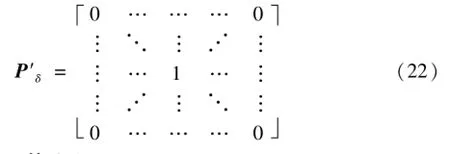
4.3 算法实现
本文的扩展方法实现起来比较简单,在Multipole的基础上只增加了不到30行C++代码。下面的伪代码实现了包含了本文扩展方法的Multipole反射、透射分布的计算。
算法1计算单层介质的反射、透射分布
输入介质参数η,σa,σs′,d,采样步长s和精度-N,-N+1,…,N-1,N

算法2 计算多层介质的反射、透射分布

5 结果比较
本节比较本文的扩展方法和传统Multipole、蒙特卡罗方法之间的效果差异。
使用的蒙特卡罗方法类似于文献[20]的方法,但在步长采样方式上更接近文献[21]的方法。具体实现如下:对于每一束光子,赋予其初始能量1,初始速度方向为z轴正向(即朝向介质内部)。每一步模拟中,根据优化散射系数σs′对散射自由程进行采样,经过一个自由程后,光子束被随机散射到一个新的方向。遇到介质表面时,根据菲涅尔项生成反射或折射光束。在模拟过程中,根据光子束经过的路径长度和吸收系数σa来减弱其能量。光子离开介质时,根据离开的位置将剩余的能量记录到相应的反射或透射分布中。考虑到径向对称性,将采样范围分割为1 024个径向片段(环状),从中心点延伸
至20 MFP之外。对于每一个蒙特卡罗分布,都使用了不少于1亿束光子来计算,以确保其准确性。
对于传统Multipole和本文的扩展方法,令N= 1 024,即取1 024个径向样本,延伸至20 MFP半径范围。最后获得的二维分布被转换为一维分布,以和蒙特卡罗方法做对比。
5.1 单层介质
固定单层介质的吸收系数σa=0.05,优化散射系数σs′=0.95,折射率η=1,光在该介质中的MFP恰好等于1。
图3展示了不同厚度d下反射分布、透射分布的对比。在图3(a)、图3(b)中,材料厚度为1.1 MFP,此时在接近中心点r=0处,传统Multipole低估了反射的量,而略微高估了透射量,本文的扩展方法结果较之更为接近蒙特卡罗方法。注意到透射分布接近中心点处的陡坡,这对应着本文扩展方法中的狄拉克δ分布部分。在图3(c)~图3(f)中,材料厚度分别为0.5 MFP和0.1 MFP,这时传统Multipole失效,可以看到0.5 MFP时的透射分布,以及0.1 MFP时的2个分布均不符合蒙特卡罗方法的结果,失真严重;0.5 MFP的反射分布,本文的扩展方法也较传统Multipole在近中心点处与蒙特卡罗方法更为吻合,而近中心点处对渲染效果的影响是比较大的。

图3 不同厚度下单层材料的反射和透射分布对比
5.2 多层介质
使用类似于皮肤构成的多层介质,表面是一个薄的主吸收层,在其下面是一个几乎无限厚的主散射层。所使用的介质参数如下:

图4展示了不同厚度d1下反射分布的对比。在图4(a)中,最上层介质的厚度稍大于1 MFP,这时其透射分布会有不小的狄拉克δ分布成分,这对卷积的结果是有影响的。传统Multipole在近中心点处低估了反射量的大小,本文的扩展方法对此有一定程度的弥补。在图4(b)、图4(c)中,最上层介质厚度分别为0.5 MFP和0.1 MFP,Multipole出现了严重失真,而本文的扩展方法依然比较吻合蒙特
卡罗方法。

图4 不同厚度d1下双层介质的反射分布对比
5.3 整体反射率/透射率的对比
整体反射率/透射率指的是介质的脉冲响应,即反射、透射分布在整个平面上的面积分:

整体反射/透射率往往反映了介质在一定光照条件下的整体色调。仍然使用4.1节中介绍的参数。图5展示随厚度变化的整体反射率和透射率的对比。从图5(a)中可以看到,传统Multipole对于厚度小于2 MFP的介质,会显著低估其整体反射率,在厚度小于0.2 MFP时无法计算(结果为负值)。在图5(b)中,从整体透射率方面看,传统Multipole在厚度为1 MFP左右失效,无法正确计算接近和小于1 MFP的介质的整体透射率。本文的扩展方法在整体反射率和整体透射率计算上均和蒙特卡罗方法比较吻合。

图5 3种方法计算的整体反射率和透射率的对比
5.4 渲染
为了更加形象地说明本文扩展方法的效果,设计了一个简单的场景:一束光入射到皮肤表面,观察其所造成的颜色渗出。由于皮肤的散射、吸收等系数是和光的波长紧密相关的,把可见光波段(400 nm~700 nm)分成了30个波段,分别对每个波段计算反射分布,然后根据得到的光谱反射分布进行渲染。使用俄勒冈州医学激光中心提供的人体皮肤的各项系数[22]。
实现方面,在PBRT[1]的基础上实现了Multipole和本文介绍的扩展方法,使用层次化积分方法[23]对BSSRDF进行积分,从而实现渲染。
对于蒙特卡罗方法,由于直接渲染的收敛速度太慢,先计算其反射分布,然后再用反射分布进行渲染。
图6展示了不同的表皮层厚度下渲染效果的对比。其中,表皮层厚度在0.2 mm(第1行)和0.1 mm(第2行)时,波长较长的红光相对于表皮层的MFP均超过了其厚度,也就是说传统Multipole并不适用。图6前3列展示了3种方法的渲染效果,后2列展示了Multipole以及本文扩展方法的结果与蒙特卡罗方法结果的差值。从图中可以看到,传统Multipole模型的误差范围较大,而本文扩展方法的误差仅仅集中在非常接近中心点的位置。

图6 实际渲染效果对比
图7对比了传统Multipole与本文的扩展方法渲染的人脸,其中表皮层厚度为0.1 mm,其他参数和图6相同。传统Multipole没能正确计算红光部分的反射分布,导致结果严重失真,扩展方法则不存在这一问题,色彩比较准确。

图7 2种方法的人脸渲染效果对比
6 存在的问题及方法性能对比
6.1 近中心点处误差问题
从实际渲染结果和之前对比过的分布曲线可以看到,不论是Multipole还是本文的扩展方法,在非常接近中心点的位置都有比较大的误差。这其实是漫射理论的一个缺陷。本文的扩展方法仍是基于Multipole,要想在这个基础上解决近中心点处误差问题比较困难。文献[14]使用量化漫射,通过在不同深度放置不同强度点光源的方法,部分解决了这一问题,但是他们的模型比Multipole复杂得多,实现较为复杂,不容易与现有Multipole实现进行集成,而本文的扩展方法实现简单,很容易与现有Multipole实现集成。
6.2 H(d)函数的选择问题
在4.1节中,所选择的H(d)函数(式(16))只是一个经验公式,实现出来的结果不错,因此采用了这一函数。不排除有更好的H(d)函数能够比现有的结果更吻合蒙特卡罗方法,这一点有待未来研究探讨。
6.3 2种方法的性能对比
本文的扩展方法对性能影响几乎可以忽略不计,因为主要改变的是单层介质的反射、透射分布的计算,而整个算法中的主要计算量在于涉及到快速傅里叶变换的卷积操作。表1比较了本文的扩展方法与传统Multipole方法在计算皮肤的光谱反射分布时所花费的时间。计算在一台具有Xeon E5462 (2.8 GHz)双处理器(总共8个核心)的工作站上进行,使用8个线程并行计算30个反射分布,结果为运行3次的平均值。表中最后一列表明了扩展方法与传统Multipole方法的性能差别在2%以内,这对于一个多线程程序来说,可以认为在误差范围内,因此2种方法没有性能上的差别。

表1 扩展方法与传统Multipole的性能比较
7 结束语
本文针对现有Multipole漫射模型的不足,提出了一个扩展方法,使其适用于非常薄的介质。该扩展方法的结果和蒙特卡罗方法的结果比较吻合,可以用于替代传统Multipole方法,且具有实现简单、容易与现有Multipole实现进行集成、对性能几乎没有影响等特点。本文提出的H(d)函数仅仅是一个经验公式,是否有更好的H(d)函数,有待未来研究探讨。
[1]Pharr M,Humphreys G.Physically Based Rendering: From Theory to Implementation[M].[S.l.]:Morgan Kaufmann,2010.
[2]Hanrahan P,Krueger W.Reflection from Layered Surfaces Due to Subsurface Scattering[C]//Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques.New York,USA:ACM Press,1993:165-174.
[3]Carmen S L,Li Ling.A Multi-layered Reflection Model of Natural Human Skin[C]//Proceedings of IEEE InternationalConferenceonComputerGraphics.Washington D.C.,USA:IEEE Press,2001:249-256.
[4]Li Ling,Carmen S L.Rendering Human Skin Using a Multilayer Reflection Model[J].Journalof Applied Mathematics and Computer Science in Simulation,2009, 3(1):44-53.
[5]Stam J.AnIlluminationModelforaSkinLayer Bounded by Rough Surfaces[C]//Proceedings of the 12th Eurographics Workshop on Rendering Techniques.Vienna,Austria:Springer,2001:39-52.
[6]Dorsey J,Edelman A,Jensen H W,et al.Modeling and Rendering ofWeatheredStone[C]//Proceedingsof Special Interest Group for Computer Graphics.New York, USA:ACM Press,2006:4.
[7]Jensen H W,Legakis J,Dorsey J.Rendering of Wet Materials[M].Vienna,Austria:Springer,1999.
[8]Pharr M,Hanrahan P.Monte Carlo Evaluation of NonlinearScatteringEquationsforSubsurfaceReflection[C]//Proceedings of the 27th Annual Conference on ComputerGraphicsandInteractiveTechniques.New York,USA:ACM Press,2000:75-84.
[9]Krishnaswamy A,Baranoski G V G.A Biophysically-based Spectral Model of Light Interaction with Human Skin[J].Computer Graphics Forum,2004,23(3):331-340.
[10]Nicodemus F E,Richmond J C,Hsia J J.Geometrical Considerations and Nomenclature for Reflectance[M].Washington,D.C.,USA:[s.n.],1977.
[11]Jensen H W,Marschner S R,Levoy M,et al.A Practical Model for Subsurface Light Transport[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques.New York,USA:ACM Press,2001: 511-518.
[12]Donner C,Jensen H W.Light Diffusion in Multi-layered TranslucentMaterials[J].ACMTransactionson Graphics,2005,24(3):1032-1039.
[13]Donner C,Jensen H W.Rendering Translucent Materials Using Photon Diffusion[C]//Proceedings of the 18th EurographicsConferenceonRenderingTechniques Eurographics Association.New York,USA:ACM Press, 2008:4.
[14]Irving G.A Quantized-diffusion Model for Rendering TranslucentMaterials[J].ACMTransactionson Graphics,2011,30(4):56.
[15]王家良.人体皮肤实时渲染的初步研究[D].青岛:青岛大学,2009.
[16]Ishimaru A.Wave Propagation and Scattering in Random Media[M].New York,USA:Academic Press,1978.
[17]Egan W G,Hilgeman T,Reichman J.Determination of Absorption and Scattering Coefficients forNonhomogeneous Media.2:Experiment[J].Applied Optics,1973, 12(8):1816-1823.
[18]Patterson M S,Chance B,Wilson B C.Time Resolved Reflectance and Transmittance for the Non-invasive Measurement of Tissue Optical Properties[J].Applied Optics,1989,28(12):2331-2336.
[19]Donner C S.TowardsRealisticImageSynthesisof Scattering Materials[D].San Diego,USA:University of California,2006.
[20]Wang Lihong,Wu Hsin-i.Biomedical Optics:Principles and Imaging[M].[S.l.]:John Wiley&Sons,2012.
[21]Fang Qianqian,Boas D A.Monte Carlo Simulation of Photon Migration in 3D Turbid Media Accelerated by Graphics Processing Units[J].Optics Express,2009, 17(22):20178-20190.
[22]Jacques S L.Skin Optics[J].Oregon Medical Laser Center News,1998,(1):1-9.
[23]Jensen H W,Buhler J.A Rapid Hierarchical Rendering TechniqueforTranslucentMaterials[J].ACM Transactions on Graphics,2002,21(3):576-581.
编辑 顾逸斐
Extension of Multipole Diffusion Model for Thin Medium
WU Yifan,YANG Xubo
(School of Software,Shanghai Jiaotong University,Shanghai 200240,China)
The Multipole diffusion model is a simple model that well describes light scattering in translucent materials.However,it is not well suited for very thin medium,particularly those close to or thinner than one Mean Free Path (MFP).This paper tries to extend the Multipole diffusion model for very thin medium with reasonable accuracy.It reviews the Multipole diffusion model and its assumptions,and to relax one of the assumptions by separating the direct transmitting component and the diffuse component of light.It adjusts the way the Multipole model places its point light sources to better match characteristics of light transport in thin medium.The diffuse part of the light is calculated using the modified source placement,and the direct transmitting part is approximated using a Dirac delta distribution.To evaluate the accuracy of the extended model,it is compared with the classical Multipole and Monte-Carlo simulations.The resulting profiles is predicted by the three models,as well as actual renderings.It is shown that the classical Multipole model is unable to compute profiles correctly for materials close to or less than one MFP thick.The extended model matches Monte-Carlo results better than the classical Multipole model.The extension of the current Multipole diffusion model proposed is suitable for medium close to or thinner than one MFP,and matches the Monte-Carlo method with reasonable accuracy.It can be easily integrated with existing Multipole implementations.
subsurface scattering;translucent;thin materials;diffusion model;reflectance profile;Mean Free Path(MFP)
吴一帆,杨旭波.针对薄层介质的多极漫射模型扩展[J].计算机工程,2015,41(3):228-236.
英文引用格式:Wu Yifan,Yang Xubo.Extension of Multipole Diffusion Model for Thin Medium[J].Computer Engineering,2015,41(3):228-236.
1000-3428(2015)03-0228-09
:A
:TP391.41
10.3969/j.issn.1000-3428.2015.03.043
国家自然科学基金资助项目(61373085,61173105,60970051)。
吴一帆(1988-),男,硕士研究生,主研方向:计算机图形学;杨旭波,教授。
2014-04-28
:2014-05-26E-mail:patwonder@163.com

