一种基于局部特征的三维模型检索算法
屠 宏,耿国华
(西北大学信息科学与技术学院,西安710127)
一种基于局部特征的三维模型检索算法
屠 宏,耿国华
(西北大学信息科学与技术学院,西安710127)
在基于内容的三维模型检索系统中,特征提取技术是三维模型检索的关键。为此,提出基于局部特征的三维模型检索算法。定义一种新的局部特征描述符:曲度,将其作为三维模型检索时的特征。曲度作为对平均曲率与高斯曲率的校正,在不增加额外计算量的前提下,可同时克服平均曲率对平滑模型的不敏感性和高斯曲率分布较均匀的缺点,更真实地反映三维模型的局部弯曲程度。实验结果表明,以曲度作为特征进行检索,可明显提高检索的查准率,配合全局特征检索时则可在保证查全率的基础上,大幅提高检索的准确性。
三维模型检索;曲度;高斯曲率;平均曲率;特征提取
1 概述
随着三维数据获取技术、三维建模以及计算机软硬件技术的快速发展,三维模型的获取和产生已经越来越容易,全世界每天都产生大量的三维模型,并且其应用的范围也越来越广泛,如工业设计、虚拟现实、游戏动漫等。如何在各种模型数据库和互联网上快速、准确地找到自己所需的三维模型,已成为多媒体信息检索中的一个重要课题。
三维模型检索系统一般包括模型的特征提取、特征库建立、特征向量的相似性匹配、查询及反馈接口等部分,其中,三维模型的特征提取是其首要的和关键的一步。三维模型特征向量的质量决定了三维模型检索的质量。文献[1-3]利用模型顶点的曲率的特性作为描述符进行模型检索。对于嵌入在欧几里得空间R3中的二维平面,有2种曲率存在:平均曲率(mean curvature)和高斯曲率(Gauss curvature)。平均曲率H=κ1+κ2和曲面面积的第一变分密切相关,平均曲率依赖于嵌入方式,例如,一个圆柱和一个平面是局部等距的,但是平面的平均曲率为0,而圆柱的平均曲率为非零。高斯曲率K=κ1·κ2实际上是曲面的内在属性,也就是高斯曲率不依赖于曲面的特定嵌入。
本文提出一种基于局部特征的三维模型检索算法,定义曲度D=κ21+κ22作为三维模型的特征描述符,利用其同时包含高斯曲率和平均曲率信息的特点,克服平均曲率对平滑模型的不敏感性,以及高斯曲率分布较均匀的缺点,更真实地反映三维模型的
局部弯曲程度,提高三维模型检索的查准率。
2 基于内容的三维模型检索
基于内容的三维模型检索首先从三维模型中自动计算并提取其特征向量也称为形状描述符,如形状、空间关系、材质的颜色及纹理等特征,建立三维模型的多维特征信息索引,然后在多维特征空间中计算待查询模型与目标模型之间的相似程度并进行排序,实现对三维模型数据库的浏览和检索[4]。其核心技术是三维模型的特征向量或是形状描述符的提取,图1是一个典型的基于内容的三维模型检索系统的框架。离线部分是对模型库中的模型进行特征提取并建立特征库的过程,每一个模型都由唯一的一个或一组特征向量表示。在线部分是对待检索的模型进行特征提取,然后在模型特征库中进行相似性比较,并进行排序得到最终的检索结果。在整个检索系统中,三维模型的特征提取是其核心,因此,国内外对三维模型特征提取算法的研究也比较多。

图1 三维模型检索系统框架
三维模型的检索算法可以分为基于全局特征的检索和基于局部特征的检索。全局特征描述了三维模型的整体形状特征,这些特征包括模型的各种统计矩、模型的体积和面积、傅里叶变换等。文献[5]利用高斯核函数描述模型投影轮廓特征的分布作为特征,进行模型检索。文献[6]提取了三维模型投影轮廓的边界点为描述符进行检索。文献[7]用W-系统矩融合volume descriptors不变特征用于模型检索。文献[8]推广了高斯映射,将模型表面点到原点的法向距离也存储在高斯映射中,高斯映射和推广的高斯映射都需要将模型归一化。文献[9]将模型映射到以模型中心为对称中心的12个平面上,通过对比二维映射图来确定模型间的相似度。近些年,很多学者不再直接比较三维模型全局特征的相似度,而是通过比较全局特征分布的相似度来确定三维模型的相似度,文献[10]将模型表面任意点的距离、角度、面积和体积的分布作为特征描述符进行三维模型的相似性匹配,通过他们的对比实验结果显示,模型表面任意点之间的距离分布图作为特征的效果最好。全局特征描述符适合对模型进行粗分类,对模型之间细微的不同不敏感,对同类模型间的检索效果不是很好。
基于局部特征的三维模型描述符主要考虑的是模型表面上的点和其邻近点之间的关系,文献[11]用球坐标系将模型表面曲率映射到了一个单位球上,比较两个模型的曲率分布来确定模型的相似性,它要求模型必须是封闭的,不能有“洞”。Zaharia and Preteux描述用三维形状谱描述符作为特征,形状索引被定义为模型表面2个主曲率的函数,这种方法需要复杂的计算,要求模型表面有良好的拓扑结构。文献[12]通过一点的邻域内的三维曲线的性质描述这点附近曲面的性质,以此为三维模型的局部特征进行检索,这种方法计算量大,很难应用到三维模型检索算法中去。
三维模型的全局特征描述符体现的是三维模型整体的特征,基于全局特征的检索算法对模型的粗分类比较有效,对于同类型的不同模型的敏感度较低,大多数全局特征描述符的计算较简单。三维模型的局部特征描述符体现的是三维模型局部的特性,基于局部特征的检索算法可以区分模型之间细微的差别,适合模型的精确检索,特征描述符的计算较复杂,对模型的要求较高。
3 平均曲率、高斯曲率和曲度
曲线的曲率描绘的是曲线的弯曲程度,曲面的曲率描绘了曲面的弯曲程度,曲面上任一点的曲率是由过这点的曲线的曲率来刻画的,对于曲面上任意一点,平均曲率H和高斯曲率K常被用来刻画曲面的弯曲特性。在三维模型检索算法中,平均曲率和高斯曲率常被用作三维模型的局部特征描述符进行三维模型的检索。
设曲面S的方程为r=r(u,v),则曲面上的点的平均曲率H、高斯曲率K可以由下面的公式给出:
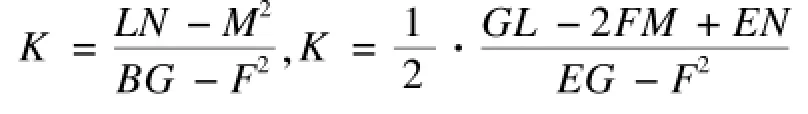
其中:

高斯曲率和平均曲率都是曲面的内在几何不变量,能很好地描绘曲面上某点的弯曲程度,但是也有
各自的缺陷。高斯曲率K=κ1·κ2是2个主曲率的乘积,圆柱形曲面上的任意一点,它的最小曲率都为0,因此,圆柱曲面上的任意一点的高斯曲率也为0,也就是说,以高斯曲率作为特征来看,圆柱曲面和平面是局部同构的,但从实际情况和视觉效果上看,它们是不同的。因此,以高斯曲率作为特征描述符进行模型检索,对此类曲面不敏感,会降低模型的查准率。平均曲率K=κ1+κ2/2是2个主曲率的和,当曲面上某点为鞍点时,其平均曲率为0,以平均曲率作为特征来看,曲面上的鞍点和平面的点是局部同构的,但从实际情况和视觉效果上看,它们是不同的。因此,以平均曲率作为特征描述符进行模型检索,对此类曲面不敏感,会降低模型的查准率。

曲度公式可以写成高斯曲率K和平均曲率H的和的形式。对于圆柱曲面,当高斯曲率为0时,平均曲率不为0;对于曲面上的鞍点,平均曲率为0时,高斯曲率不为0。因此,曲度克服了平均曲率和高斯曲率固有的缺点,能准确区分圆柱形表面上的点、鞍点和平面上的点,曲度作为特征描述符能提高模型检索的精确度。
对于表面较光滑的三维模型,平均曲率较小,以平均曲率作为特征描述符对此类模型并不敏感,相对而言,高斯曲率对此类模型具有较高的敏感性,曲度是平均曲率的平方和高斯曲率的和,当平均曲率较小时,其平方后的值会更小,这时曲度就近似等于高斯曲率,它克服了平均曲率作为特征对光滑模型不敏感的缺点。同时,曲度作为平局曲率和高斯曲率的和,在高斯曲率的值上又加上了平均曲率的值,克服了高斯曲率分布较均匀的缺点。从以上数值角度的分析来看,曲度作为特征描述符能提高模型检索的精确度。
4 曲度的计算
三维模型的表示方法有很多种,其中三角网格形式是三维模型常用的表示方法之一,本文以三角网格模型作为研究对象。经典的微分几何研究的是连续的曲线和曲面的微分特性,对于网格模型这种离散形式的曲面并不适用,因此需要借助离散微分几何的一些方法来计算高斯曲率和平均曲率。
三角网格上曲率计算的方法有多种,平均曲率的估计本文采用文献[13]的方法,引入Laplace-Beltrami算子Δ=2Hn(Δ为梯度算子,H为采样点的平均曲率,n为采样点的法向量)。对拉普拉斯算子Δ在三角网格曲面上进行离散,对网格曲面上的顶点pi,其 1-邻域点集为{pi,j∈N(i)},则Δ是其加权和:



图2 αij,βij示意图

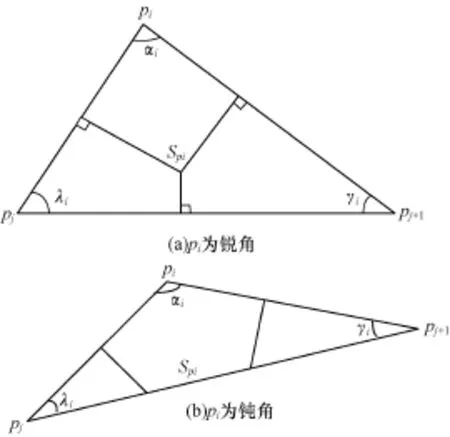
图3 Spi面积示意图
点S是三角形的外心(三角形的三边的垂直平分线交于一点。该点叫做三角形的外心)
当Ti为锐角三角形时:


5 实验结果与分析
本文实验的计算机配置为Intel CPU主频3.2 GHz,内存16 GB,测试平台是Windows 7操作系统,代码由Matlab 2012b编写,本文从普林斯顿基准数据库中抽取了4类125个模型建立了实验数据库,包括31个人、37个手、27个四足动物、30条鱼。采用相同的模型数据集,分别用平均曲率、高斯曲率和本文提出的算法进行对照实验,采用查准率(Precision)和查全率(Recall)评价3种算法的检索性能,部分检索结果如图4所示。

图4 部分检索结果
对于光滑模型,平均曲率不敏感,在第1组实验中,以平均曲率为特征的检索结果中有2个错误匹配的模型,高斯曲率的检索结果较平均曲率略好,有一个错误匹配的模型,以曲度为特征的检索效果最好,没出现错误匹配的模型,其查全率-查准率曲线如图5所示。

图5 查全率-查准率曲线(曲率均匀模型)
对于不光滑模型的检索,高斯曲率分布较均匀,对模型的变化并不是太敏感,平均曲率的检索效果较高斯曲率略好,只有一个错误匹配的模型,本文提出的特征提取方法检索效果最好,其查全率-查准率曲线如图6所示。

图6 查全率-查准率曲线(曲率不均匀模型)
6 结束语
本文定义了三维模型的曲度作为特征用于检索,将曲度表示为平均曲率和高斯曲率的和,包含了平均曲率和高斯曲率的信息,能较全面地反映模型表面的总体特征,其检索性能要优于单纯使用平均曲率或是高斯曲率的检索性能。但是,由于曲度的计算依赖于离散网格曲面曲率的计算,而离散网格上曲率的计算易受噪声的影响且计算量大,因此,更鲁棒、简单的曲率计算是下一步的改进方向。
[1]Torkhani F,Wang K,Chassery J M.A Curvature-tensorbased PerceptualQuality Metric for 3DTriangular Meshes[J].Machine Graphics&Vision,2013,32(16): 1-25.
[2]Liu Yujie,Zhang Xiaodong,Li Zongmin,et al.Extended Cone-curvature Based Salient Points Detection and 3D ModelRetrieval[J].MultimediaToolsand Applications,2013,64(3):671-693.
[3]Cho J W,ProstR,JungHY.AnOblivious Watermarkingfor3-DPolygonalMeshesUsing Distribution of Vertex Norms[J].IEEE Transactions on Signal Processing,2007,55(1):142-155.
[4]Funkhouser T,Min P,Kazhdan M,et al.A Search Engine for 3D Models[J].ACM Transactions on Graphics,2003,22(1):83-105.
[5]唐 祺,杨 新.基于高斯核密度函数和轮廓的三维模型检索[J].计算机工程,2013,39(10):172-180.
[6]姜 阳,吕学强,付成睿,等.基于边界点描述符的三维模型检索研究[J].微电子学与计算机,2013, 30(10):71-74.
[7]马自萍,康宝生,马金林.W-系统矩和Fourier变换下Volume Descriptors不变特征的三维模型检索[J].计算机辅助设计与图形学报,2014,26(4):519-616.
[8]Kang S B,Ikeuchi K.Determining 3-D Object Pose Using the Complex Extended Gaussian Image[C]// ProceedingsofComputerVisionandPattern Recognition.Lahaina,USA:IEEE Computer Society, 1991:580-585.
[9]Kazhdan M,Chazelle B,Dobkin D,et al.A Reflective Symmetry Descriptor for 3D Models[J].Algorithmica, 2004,38(1):201-25.
[10]Osada R,FunkhouserT,ChazelleB,etal.Shape Distributions[J].ACM Transactions on Graphics,2002, 21(4):807-832.
[11]Shum H Y,HebertM,IkeuchiK.On3DShape Similarity[C]//Proceedings of Computer Vision and Pattern Recognition.Ottawa,Canada:IEEE Computer Society,1996:526-531.
[12]Chua C S,JarvisR.PointSignatures:ANew Representation for 3D Object Recognition[J].International Journal of Computer Vision,1997,25(1):63-85.
[13]Xu Guoliang.DiscreteLaplace——BeltramiOperators and Their Convergence[J].Computer Aided Geometric Design 2004,21(8):767-784.
[14]Dyn N,Hormann K,Kim S J,et al.Optimizing 3D Triangulations Using Discrete Curvature Analysis[J].Mathematical Methods for Curves and Surfaces,2001, 38(8):135-146.
编辑 金胡考
A 3D Model Retrieval Algorithm Based on Local Feature
TU Hong,GENG Guohua
(School of Information Science and Technology,Northwest University,Xi’an 710127,China)
Feature extraction is the most important technology in content-based 3D model retrieval.This paper proposes an algorithm for feature extraction based on curvature features of 3D triangle model.The curvature of 3D model can become the sum of Gaussian curvature and mean curvature.So it is a blend of the Gaussian curvature and mean curvature.It can estimate the curvature of 3D model’s vertices through the discrete differential geometry,and build a feature vector of 3D model.Experimental results show that the algorithm of this paper is better than the average curvature or Gaussian curvature as the feature vector.
3D model retrieval;camber;Gaussian curvature;mean curvature;feature extraction
屠 宏,耿国华.一种基于局部特征的三维模型检索算法[J].计算机工程,2015,41(3):218-222.
英文引用格式:Tu Hong,Geng Guohua.A 3D Model Retrieval Algorithm Based on Local Feature[J].Computer Engineering,2015,41(3):218-222.
1000-3428(2015)03-0218-05
:A
:TP18
10.3969/j.issn.1000-3428.2015.03.041
国家自然科学基金资助项目(60873094)。
屠 宏(1979-),女,博士研究生,主研方向:图形图形处理,机器学习;耿国华,教授、博士生导师。
2014-03-24
:2014-05-06E-mail:tuhong7903@gmail.com

