基于粒子群优化的复杂网络社区挖掘
白 云,任国霞
(西北农林科技大学信息工程学院,西安712100)
基于粒子群优化的复杂网络社区挖掘
白 云,任国霞
(西北农林科技大学信息工程学院,西安712100)
为解决复杂网络社区结构挖掘的优化问题,根据复杂网络拓扑结构的先验知识,提出一种基于离散粒子群优化的社区结构挖掘算法。将粒子的位置和速度定义在离散环境下,设计粒子的更新规则,在不需要事先指定社区个数的前提下自动判断网络的最佳社区个数,给出局部搜索算子,该算子可以帮助算法跳出局部最优解,提高算法的收敛速度和全局寻优能力。实验结果表明,与iMeme-net算法相比,该算法能够准确地挖掘出复杂网络中隐藏的社区结构,且执行速度较快。
粒子群优化;复杂网络;社区结构;社区挖掘;局部搜索;模块密度
1 概述
网络存在于人们生活中的每一个角落,如社交网络、通信网络、金融网络、生物网络等。现实中绝大多数复杂系统如电力系统、科学引文系统、航线运输系统、移动通信系统等,都可以建模成由节点和边组成的复杂网络。目前,网络在以空前的广度、深度和速度改变人们的日常生活方式和交流方式,同时,网络也影响着社会的政治、经济和文化的发展。
文献[1]提出社会计算的概念,掀起了学术界研究的新高潮。社会计算是一种新的计算模式,计算对象是社会媒体数据,其典型的处理思路是将媒体数据建模成复杂网络数据然后对复杂网络进行分析。复杂网络有很多特性,如小世界性[2]、无标度特性等[3],其中,社区特性[4]近年来被证明是复杂网络最具典型的一个特性。所谓网络社区指的是网络的一些子块,这些子块内部的连接比较密集而子块与子块之间的连接则比较稀疏。挖掘复杂网络中隐藏的社区结构特性对于复杂网络分析具有及其重要的意义,目前已经有大量的社区结构挖掘算法被提出[5]。
在现存网络社区挖掘算法里,优化算法的核心
思想是将网络社区挖掘看成一种优化问题,然后采用启发式优化算法对该问题进行求解。在启发式算法中,粒子群优化算法[6]以其原理简明、操作简单、参数少、收敛快等特点而闻名,被广泛应用于求解各种优化问题。粒子群优化算法是受群居生物捕食和躲避捕食者行为的启发而人工建模的优化算法。然而,经典粒子群优化算法是为连续优化问题设计的,对于离散优化问题,经典粒子群优化算法无法求解。为此,本文提出一种离散粒子群优化算法,并将其应用于复杂网络社区挖掘。粒子的位置和速度被定义为离散形式,粒子的状态更新方程被重新设计,并充分利用了网络的先验知识。为提高算法的全局搜索能力和收敛速度,设计局部搜索策略,该搜索策略较为充分地挖掘了网络可以利用的信息,并在计算机模拟网络数据和真实网络数据上进行实验。
2 网络社区挖掘及粒子群优化
在对复杂网络进行分析时,通常是将其建模成由节点和边相互连接的图,然后再对图进行分析。网络社区挖掘就是要挖掘网络中潜在的社区结构,所挖掘的社区结构必须满足社区内部连接紧密,而社区与社区之间的连接则相对稀疏。网络与社区挖掘示意图如图1所示。

图1 网络与社区挖掘示意图
从图1可以看出,网络社区挖掘的本质是图的分割问题,其可以转化成数学优化问题,进而可以采用优化算法进行求解。然而,很多图的优化问题建模出来的数学函数都不具有可导性,甚至不具备连续性,因此,传统数学方法很难求解这类问题。为了求解这类优化问题,启发式优化算法被学者们提出。在启发式优化算法中,粒子群优化算法脱颖而出并得到广泛应用[7-8]。粒子群优化算法通过一组粒子来优化一个问题,每个粒子代表问题的一个解,每个粒子通过自身的学习根据一些简单的规则来调整自己的飞行状态,从而使粒子向问题的全局最好解靠近。

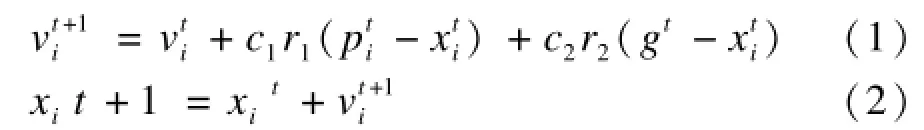
粒子i根据式(1)调整自己的飞行速度,再根据新的速度来调整自己的飞行轨迹,从而使粒子向最优解区域靠近。
3 基于粒子群优化的网络社区挖掘算法
经典粒子群优化算法都是为连续优化问题而设计的,其状态更新式(1)和式(2)无法直接应用于离散问题的求解。本文重新定义了粒子的状态及其更新公式,提出一种离散粒子群优化算法框架,并将其成功运用于复杂网络社区挖掘。
3.1 粒子的编码与解码
编码与解码是将优化问题与优化算法建立连接的桥梁。针对社区挖掘这个问题,文献[9]提出一种基于连接的编解码方式,文献[10]提出字符串的编解码方式。
本文采用的编解码方式为基于字符串的编码,因为这种编码操作简单而且解码方便。本文采用的粒子编解码方式如图2所示。
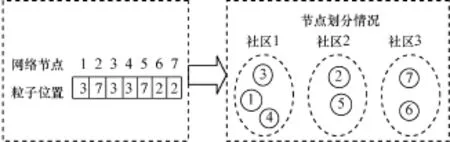
图2 粒子的编解码示意图
由图2可见,粒子的位置是一个整数序列,序列的每一位数字代表对应位置节点的社区分类标号,在解码时,具有相同社区标号的节点被划分到同一个社区中。由此可见,该编码可以自动判断网络到底划分成几个社区,而不需要人工事先指定社区个数。
3.2 粒子的状态更新方程
为了将粒子群优化算法和社区挖掘相结合,本文重新定义粒子的状态更新方程如下:
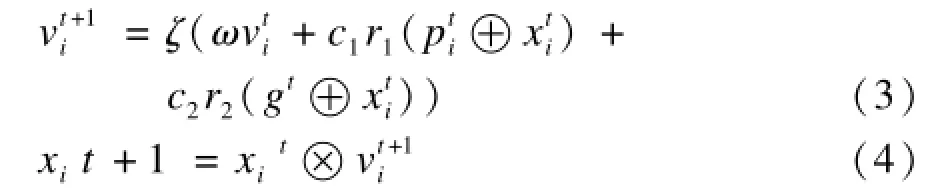
其中,ω是惯性权值常数;符号⊕表示异或操作;函数ζ(x)是一个限界函数,其目的是将变量x变为离散的二进制形式,以便于其与位置向量进行式(4)的操作,其具体定义如下:
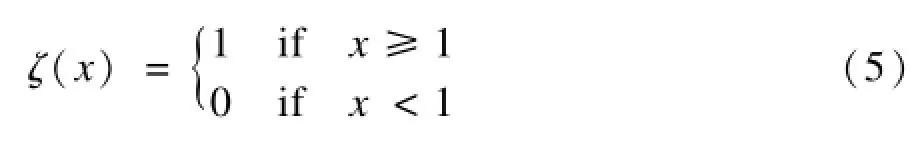
式(4)中的⊗操作是粒子状态更新的核心操作,该操作定义的好坏直接影响算法挖掘社区的性能以及算法的收敛情况。
对于一个网络而言,2个没有连接的节点属于同一个社区的概率要小于2个有连接的节点的概率,基于该事实,本文定义的⊗操作如下:
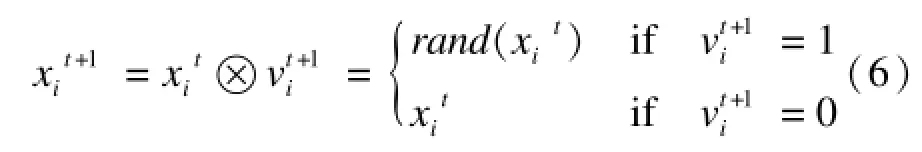
3.3 粒子的适应度函数
适应度函数是用来评价粒子状态好坏的,对于复杂网络社区挖掘问题而言,适应度函数评价的是网络社区划分的好坏。本文采用的适应度函数为文献[11]提出的模块密度函数。
令Ω={c1,c2,…,ck}为网络的一个划分,1≤k≤N,N是网络的节点个数,定义L(c1,c2)=∑i∈c1,j∈c2aij,其中,aij为网络的邻接矩阵A′的元素,模块密度定义如下:

其中,α是分辨率控制参数,其范围为[0,1];ci′=Ω-ci,|ci|表示社区ci的节点个数。
3.4 粒子的局部搜索策略
由于粒子群优化算法也是一种随机搜索算法,因此也避免不了陷入局部最优的情况,另外,由于现实的网络都比较大,算法处理起来可能收敛很慢,为了提高算法的全局寻优能力和收敛速度,本文设计了一种粒子局部搜索策略。该局部搜索策略是对文献[12]提出的搜索策略的一种改进。本文局部搜索策略的核心思想如图3所示。
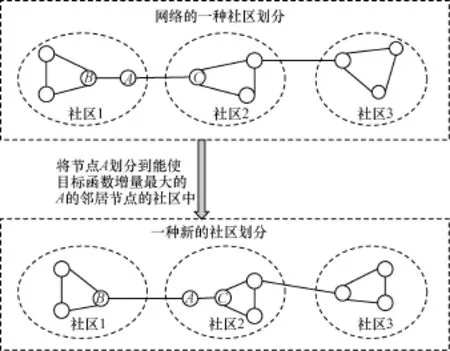
图3 粒子的局部搜索策略示意图
从图3可以看出,本文局部搜索策略的核心思想是对被选择进行搜索的节点A分配到能够使目标函数增量最大的邻居节点的社区中。文献[12]的搜索策略是将节点A分配到能使目标函数增量最大的其他社区中,而本文的做法则可以大大节省搜索空间,因为本文的搜索是基于节点的连接的,而对于一个大规模网络而言,社区数目通常很大,但节点的平均度却很小,即节点的连接是很稀疏的。
4 实验结果与分析
为了测试所提算法的社区挖掘性能,本节将对算法进行对比实验测试。实验中采用了计算机模拟网络数据和真实网络数据。实验采用了文献[12]的算法iMeme-net作为对比算法。本文算法参数设置为:分辨率控制参数α取值范围为[0.2,1.0];间隔为0.1;粒子群大小为50;迭代次数为50;社会系数和认真系数均设置为1.494;惯性权值设为0.792。为了公平起见,算法iMeme-net的种群大小和迭代次数都设为50,其他参数采用原文设置。
计算机模拟网络数据来源于文献[13],该数据被称为GN扩展基准网络数据,该网络数据包含128个节点,被平均分成4个社区,网络通过一个混合参数γ来控制社区内部以及社区之间边的连接。
对于网络的真实社区划分存在的情况下,为了评价算法挖掘出来的社区的好坏,本文采用文献[14]提出的互信息指标NMI来进行评价。
给定网络的2个社区划分A和B,令C′为一个混淆矩阵,矩阵C′的元素Cij为划分A中社区i和划分B中社区j共同拥有的节点个数,则划分A和B之间的归一化互信息NMI(A,B)的计算方式可以表示为:
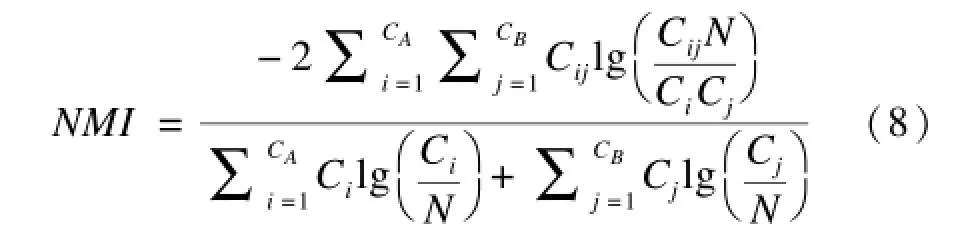
其中,CA(CB)表示划分A(B)中的社区个数;Ci(Cj)表示矩阵C′的第i行(第j列)的元素之和;N为网络节点个数。
实验中,在每个网络数据上每个算法独立运行30次。图4和图5记录了算法在计算机模拟网络上的实验结果。从图4和图5可以看出,本文算法在基准网络混合参数γ不大于0.35的情况下,可以较好地挖掘网络的真实社区结构,和iMeme-net算法相比,在参数α=0.9时,本文算法得到的NMI值明显高于iMeme-net算法。表1记录了本文算法和对比算法iMeme-net在真实网络上进行测试时得到的实验结果,其中,括号里面的为本文算法得到的结果;空手道网络和海豚网络的真实社区都为2个。
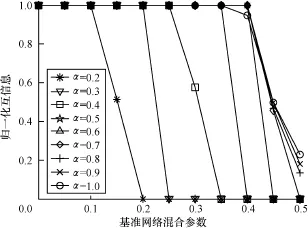
图4 本文算法在模拟网络上的实验结果
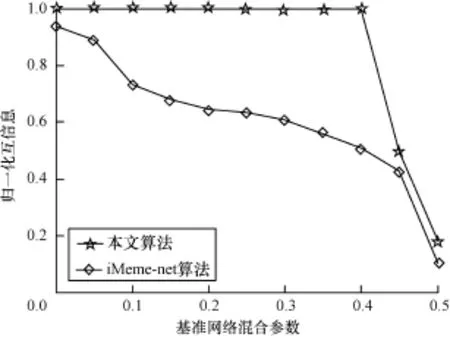
图5 本文算法与iMeme-net算法的实验结果对比

表1 真实网络数据上的实验结果对比
从表1的实验数据可以看出,本文算法相对iMeme-net算法在目标函数方面有明显的提高。在分辨率控制参数α=0.3时,本文算法得到了NMI为1的网络划分,即本文算法找到了网络的真实社区结构。本文算法在α=0.3时得到的空手道网络和海豚网络的社区结构如图6和图7所示,其中,圆形和四方形分别表示不同的社区划分。在科学家合作网上本文算法得到的目标函数值明显高于对比算法。可以看出,本文算法在挖掘网络的社区结构时是有效的,通过调节目标函数中的分辨率控制参数可以得到不同的网络社区划分。
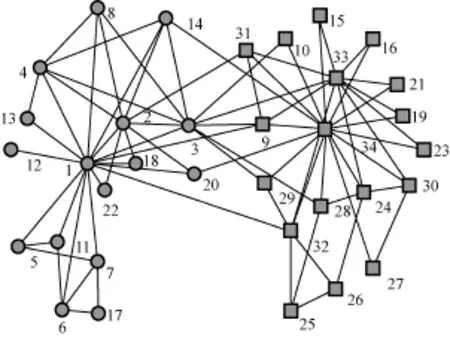
图6 本文算法得到的空手道网络社区结构划分
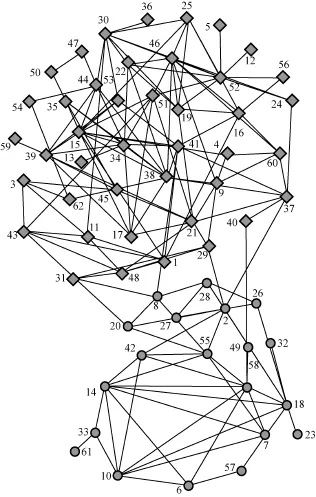
图7 本文算法得到的海豚网络社区结构划分
5 结束语
复杂网络社区挖掘对研究网络隐藏的知识和运行机制具有极其重要的作用。为此,本文提出一种离散粒子群优化算法,并将其运用于社区挖掘。从优化的角度着手挖掘复杂网络中的社区结构,通过粒子群优化算法优化性能指标,从而寻找该指标最优时对应的网络社区结构,并给出一种改进的局部搜索策略。实验结果证明了其有效性。今后将研究如何提高粒子群优化算法在大数据处理上的性能,以及多目标粒子群优化算法的设计。
[1]Lazer D,Pentland A S,Adamic L,et al.Life in the Network:The Coming Age of Computational Social Science[J].Science,2009,323(5915):721-723.
[2]Watts D J,Strogatz S H.Collective Dynamics of‘Smallworld’Networks[J].Nature,1998,393(6684):440-442.
[3]Barabási A L,AlbertR.EmergenceofScalingin Random Networks[J].Science,1999,286(5439): 509-512.
[4]Girvan M,Newman M E J.Community Structure in Social and Biological Networks[J].Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.
[5]Fortunato S.CommunityDetectioninGraphs[J].Physics Reports,2010,486(3):75-174.
[6]Kennedy J,Eberhart R.Particle Swarm Optimization[C]// Proceedings of IEEE International Conference on Neural Networks.Washington D.C.,USA:IEEE Press,1995, 1942-1948.
[7]邬开俊,鲁怀伟.云环境下基于DPSO的任务调度算法[J].计算机工程,2014,40(1):59-62.
[8]徐从东,陈 春.一种自适应动态控制参数的粒子群优化算法[J].计算机工程,2013,39(10):203-207.
[9]Pizzuti C.A Multiobjective Genetic Algorithm to Find Communities in Complex Networks[J].IEEE Transactions on Evolutionary Computation,2012,16(3):418-430.
[10]Gong Maoguo,Cai Qing,Chen Xiaowei,et al.Complex Network Clustering by Multiobjective Discrete Particle Swarm Optimization Based on Decomposition[J].IEEE Transactions on Evolutionary Computation,2014,18(1): 82-97.
[11]Li Zhenping,Zhang Shihua,Wang Ruisheng,et al.Quantitative Function for Community Detection[J].Physical Review E,2008,77(3).
[12]Gong Maoguo,Cai Qing,Li Yangyang,et al.An Improved Memetic Algorithm for Community Detection in Complex Networks[C]//ProceedingsofIEEECongresson Evolutionary Computation.Washington D.C.,USA:IEEE Press,2012:1-8.
[13]Lancichinetti A,FortunatoS,RadicchiF.Benchmark Graphs for Testing Community Detection Algorithms[J].Physical Review E,2008,78(4).
[14]Huberman B A.Finding Communities in Linear Time: A PhysicsApproach[J].TheEuropeanPhysical Journal B——Condensed Matter and Complex Systems, 2004,38(2):331-338.
编辑 刘 冰
Complex Network Community Mining Based on Particle Swarm Optimization
BAI Yun,REN Guoxia
(College of Information Engineering,Northwest A&F University,Xi’an 712100,China)
In order to solve the problem of community mining optimization from complex network,according to the prior knowledge of the topology structure of complex network,a complex network community mining algorithm based on Particle Swarm Optimization(PSO)is proposed.In the proposed algorithm,particle’s position and velocity are redefined in discrete case,particle’s update principles is redesigned,the proposed algorithm can automatically determine the best community numbers without knowing it in advance.In order to improve the global search ability of the proposed algorithm,a local search operator is designed,and this operator can help the algorithm to jump out of local optimum and improves the convergence speed.Experimental results demonstrate that the proposed algorithm can efficiently dig out the community structures hidden behind complex networks,and the execution speed is much faster than that of iMeme-net algorithm.
Particle Swarm Optimization(PSO);complex network;community structure;community mining;local search;modularity density
白 云,任国霞.基于粒子群优化的复杂网络社区挖掘[J].计算机工程,2015,41(3):177-181.
英文引用格式:Bai Yun,Ren Guoxia.Complex Network Community Mining Based on Particle Swarm Optimization[J].Computer Engineering,2015,41(3):177-181.
1000-3428(2015)03-0177-05
:A
:TP18
10.3969/j.issn.1000-3428.2015.03.034
白 云(1982-),女,硕士研究生,主研方向:数据挖掘,进化计算;任国霞(通讯作者),副教授。
2014-04-08
:2014-05-16E-mail:rgx@nwsuaf.edu.cn

