基于多变量判决函数的最优路由策略
赵海军,李 敏,李明东,岳 淼
(1.西华师范大学计算机学院,四川南充637009;2.成都供电公司信息通信分公司,成都610000)
基于多变量判决函数的最优路由策略
赵海军1,李 敏2,李明东1,岳 淼1
(1.西华师范大学计算机学院,四川南充637009;2.成都供电公司信息通信分公司,成都610000)
针对分布式并行处理系统中路由算法数据包的路由选择问题,提出一种改进的最优化路由策略。从输入数据包得到数据包前后到达时间分布Pt(x)和包大小分布Pp(x),采用权值函数通过对平均前后到达时间、平均包大小和向量的不断学习获得所有包的最小化平均延迟。仿真结果表明,该策略不仅在处理器数量发生变化,而且在包前后到达时间分布和包大小分布改变的情况下,都能获得所有包的最小平均延迟。
分布式并行处理系统;多变量;路由策略;平均延迟;最小化;流量强度
1 概述
近年来,随着计算机技术和网络技术的不断发展,并行处理技术已成为研究热点。主要体现在以下5个方面:(1)对称多处理技术。这种系统在结构上一般是用总线将多个处理机连接而成。系统中的硬件和软件都是对称的。硬件上每个CP的能力完全相等,它们共享主存。软件上共享一份操作系统代码。(2)大规模并行处理技术。目前松耦合分布式存储的MIMD型MPP系统是其主流技术,关键技术包括节点结构、高速互联网络和并行程序开发环境等。(3)工作站群机技术。是将一组工作站、服务器、小型机甚至巨型机或MPP系统用互联网连在一起,构成并行处理系统。(4)并行程序开发环境技术。它不仅要解决并行软件的编程问题,还应解决并行软件的可移植性问题。(5)并行数据库技术。即提高计算机在数据管理和查询方面的能力。包括对数据库的分区管理和并行查询。多线程技术和虚拟服务器技术是目前并行数据库实现中采用的重要技术[1]。
分布式并行处理系统是一种结构复杂的计算机处理系统,其基本特征是系统中有多个处理器(或称为服务器)。在设计分布式并行处理系统时,要考虑多方面。其中主机间的最佳资源配置和最小通信延迟都是典型的和通常要考虑的方面,而这方面又着重体现在数据包的路由选择算法。
针对当前各种服务网络结构存在的问题,文
献[1]针对计算机负荷并行处理的高效稳定和最优化问题,提出了选择各节点状态和启动策略,以使通信开销最小和负荷均衡的智能化任务分配算法。文献[2]采用一种服务网络架构,并提出使用向量长度的方法衡量不同服务路径的优劣从而得到非线性的合计函数F;文献[3]从体系结构上提出了动态重构容错算法,算法通过动态重构数据分布和操作解决了系统节点和网络故障,且使正在执行的任务不被中断,使系统可用性和效率得到大幅度提高。
本文主要研究并行传输处理器系统中数据包的路由选择问题。该问题把到达包分配给几个并行传输处理器中的一个,以使所有到达包的平均延迟最小化。对于重尾分布,文献[4-6]提出了一种启发式的基于包大小的路由算法;另一种常见的路由算法即JSD(Join Shortest Delay),但该算法被认为是个单一的最佳算法,因为它仅使每个到达包的延迟最小。而单一基于包大小的固定队列FQS(Fix Queue based on Size)算法是一种不公平算法;文献[7]提出了贪婪吞吐量(Greedy Throughput,GT)算法,这种算法虽然可以提高部分并行处理器的效率,但会造成整个并行处理系统的延迟增加;文献[8]提出了等负荷大小间隔任务分配(Size Interval Task Assignment with Equal load,SITA-E)算法,这种算法与文献[7]的结果刚好相反。因此,寻找一个利用每个到达包大小、并使所有到达包延迟最小的全局最优化算法仍是一个难题[9-14]。对此,本文提出路由判决的路由算法,以使所有到达包的平均延迟最小,提高分布式并行传输处理器的效率。
2 模拟最佳路由算法
把上述问题的数学模型表示为下列组合最佳问题P1:
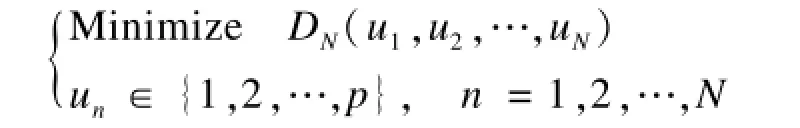
其中,N,p,DN和un分别表示到达包的数量、并行处理器的数量、所有到达包的平均延迟和分配给第n个到达包的处理器。于是,求解问题P1的数值解就是确定最佳路由。
本文确定最佳路由的主要思想为:随着输入流量强度的增加,就把数据包分别分配给不同的处理器,然后设计出一个算法(本文称为模拟最佳路由(Mimic Optimal Routing,MOR))来使所有到达包的平均延迟最小。
本文提出的MOR采用1个权值函数和3个参数,即平均前后到达时间(1/λ),平均包大小(1/μ)和向量α=(α1,α2,…,αp-1);目标就是通过从输入流量获得1/λ,1/μ和α的不断学习来提高MOR的适应性,并得到满足以下2个条件的权值函数:
(1)MOR可工作于任意数量的同类型并行处理器;
(2)尽管前后到达时间分布Pt(x)和包大小分布Pp(x)未知且可能随时间变化,但分别包含Pt(x)和Pp(x)的分布集St和Sp预先给定并可用于路由判决。
3 并行处理器模型
本文考虑的并行处理器模型M如图1所示,由系统S和输入流量T构成。在系统S中,有p个传输处理器且每个处理器k有自己的无限长队列k。每个到达包按照某种路由算法瞬间加入p个队列中的一个(忽略选择处理器的时间),每个到达包的传输按先到先服务。
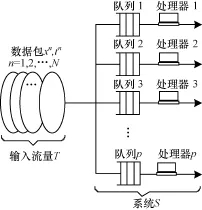
图1 并行处理器模型M(S,T)
为了得到到达包的平均延迟表达式,令Ck为处理器k的传输速率,xn和tn分别为系统S中第n个到达包的大小和到达时间。服务器k在时刻t的腾空时间(Wk(t))等于在时刻t通过处理器k传输的包的剩余传输时间与在时刻t队列k中所有包等待传输的总的时间之和。因此,如果第n个到达包被分配给处理器un,则对所有k∈Sp={1,2,…,p},有:

如果un=k,则,否则。文中的t-(t+)表示正好在t之前(之后)的时刻。因此,在时间间隔[tN0+1,tN+N0]内到达的N个包的平均延迟为:
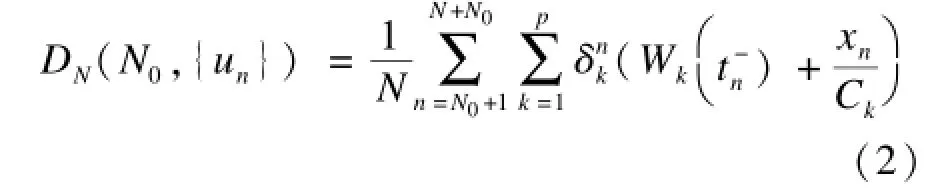
输入流量T可以用集合{tn}和{xn}来表示,它们的值按照某个概率分布来确定。设前后到达时间tn+1-tn和包大小xn的概率分别为Pt(x)和Pp(x)。在本文中,对Pt(x)和Pp(x)采用下列3个分布:
Pe(x;m),Pu(x;m)和Pt(x;m),Pe(x;m)是均值为m的指数分布,Pu(x;m)是区间(0,2m)上的均匀分布;Pt(x;m)是模式为m,左端点为0,右端点为2m的三角分布。另一方面,系统S可表示为C={C1,C2,…,Cp}。设所有处理器是同类的(C1=C2=…=Cp),因此,对所有k∈Sp,Ck=C/p,C(C=∑pk=1Ck)为总的传输速率。所以系统S可以由p和C来决定。
4 MOR算法
4.1 MOR的解析表达式
假设MOR把第n个到达包分配给处理器,则如果Mn,k=mini∈SpMn,i时,。其中:

其中,Mn,k可视为分配第n个到达包给服务器k的耗时。因此,MOR就是选择一个处理器以使耗时最小。式(3)中的wn为权值函数,与流量强度In有关。In定义为In=λn/Cμn,1/λn和1/μn分别为在时刻测得的输入流量T的平均前后到达时间和平均包大小;式(3)中的φn用来调整和的比例,φn的表达式为:
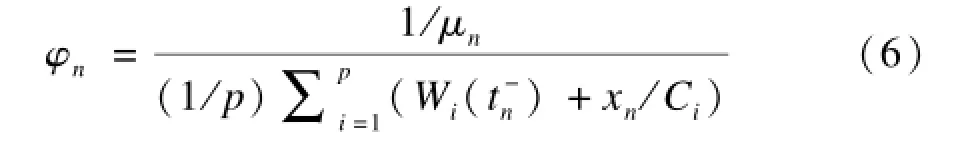
当最佳权值wn用一个最优算法求解时,φn有助于快速收敛到最优的解。
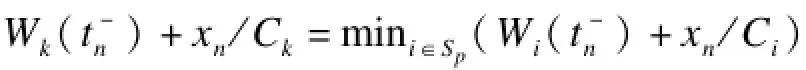
设系统S的结构为C,状态为W=(W1,W2,…,Wp),到达包大小xn对路由判决来说都是已知的。如果wn,α=(α1,α2,…,αp-1),1/λn和1/μn给定,则由式(3)~式(5),就可以得到判决函数如下:

由于1/λn和1/μn可以通过测量时刻的输入流量T来获得,因此下面主要讨论如何决定这4个参数中的另外2个参数α和wn的值。
4.2 α的确定
α的计算基于假设:如果所有前后到达时间{tn+1–tn}接近于0,则MOR就收敛。基于这个假设,α就是最优化问题P2的解:

其中,JN是在下列2个条件下得到的前N个到达包的期望平均延迟。(1)所有N个包的大小是独立、均匀分布的连续随机变量,而且它们的概率分布为Pp(x);(2)t1=t2=…=tN。同时路由判决{un}按顺序u1,u2,…,un进行。因而JN可表示为:

这里α0=0,αp=∞,且:
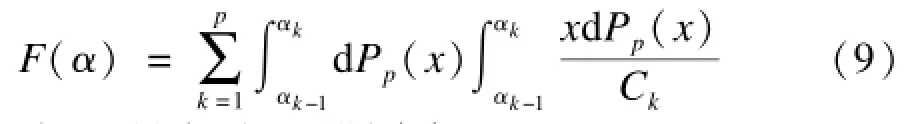
由于所有处理器同类(C1=C2=…=Cp),式(8)右边第一项是一个常量。因此,问题P2的解又等价于问题P3的解:
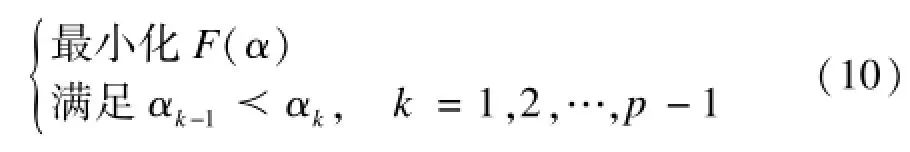
假设dPp(x)/dx≠0,如果x∈[xmin,xmax]。这里xmin和xmax分别为Pp(x)中的最小和最大包大小。对k=1,2,…,p–1,α使得F(α)为局部极小值(也就是(F(α)/(αk=0)的条件就可以表示为:
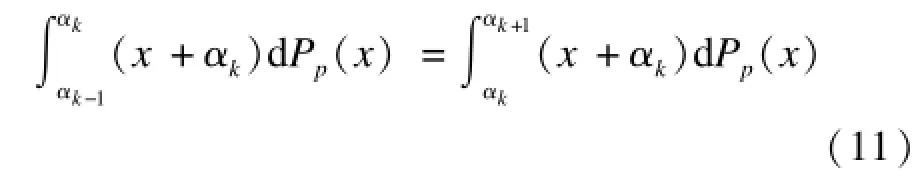
为了实时计算α值,用(x+s)代替式(11)中的被积函数(x+αk),对k=1,2,…,p-1有:
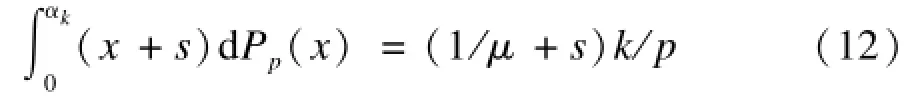
其中,1/μ是Pp(x)的平均值(也就是平均包大小)。如果s>0且式(10)成立,则式(12)有唯一解。这里p(x)=dPp(x)/dx。因此,G(αk)=0有唯一解。用牛顿法可一一得到α1,α2,…,αp-1,使α的计算量大大减少。
由于s替换αk,它必须接近αk,又由于α1,α2,…,αp-1分布在Pp(x)的均值1/μ周围,因此1/μ是一个很好的替换。当时,令为式(12)的解,且令,就可得到α(1),α(2),…,初始值为α(1)=(1/μ,…,1/μ)。
4.3 权值函数的确定
假设以下3个条件用于权值函数的计算:
(1)Pt(x),Pp(x)∈Sd(={Pe(x;1),Pu(x;1),Pt(x;1)});
(2)对每对Pt(x)和Pp(x)来说,输入流量T({tn}和{xn})是唯一的;
(3)N=4(105且N0=N/10。
从条件(1)和条件(2)可知,当改变1/λ,1/μ和C其中之一时,流量强度I(=λ/μC)都要变化(这里1/λ和1/μ分别为Pt(x)和Pp(x)的均值),
所以仅考虑1/λ=1/μ=1的情形,这时强度可简单地表示为I=1/C;条件(3)包含在状态W变成几乎稳态后,N0(=N/10)大到足以用来计算平均延迟,即使N进一步增大,计算结果也没有明显变化。
令DN(N0,{un};Pt(x),Pp(x))表示当输入流量T由Pt(x)和Pp(x)产生时由式(2)给出的平均延迟DN。首先来看最佳权值函数,因为当Pt(x)和Pp(x)已知时,要使用这个权值函数。对Pt(x)和Pp(x)来说,最佳权值w∗(Pt(x),Pp(x))(简记为w∗)的定义必须是w∗∈Sw(={0,Δw,2Δw,…,1}),且对所有w∈Sw满足:
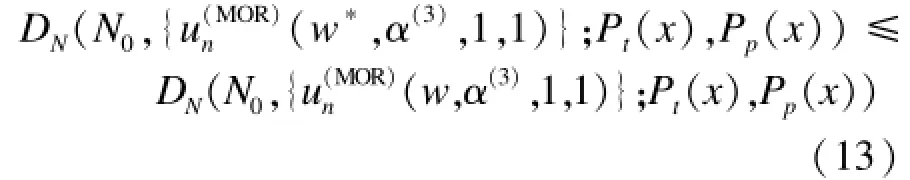
这里MOR按式(7)给出且α(3)必须在计算w∗之前计算。因为对所有w∈Sw,必须得到DN。对强度I(=1/C)来说,计算DN的次数就是集合Sw(|Sw|=1/Δw+1)中的元素的数量。最佳权值函数w∗(I;Pt(x),Pp(x))(简记为w∗(I))的定义对所有I∈SI(={ΔI,2ΔI,…,4})成立。
5 MOR算法的性能仿真
5.1 仿真环境及模型
为了对算法的性能进行测试,本文在Linux环境中,采用Opnet Modeler 10.0A网络仿真平台,并结合C++编程语言来对算法进行仿真。
用Opnet Modeler的Rapid Configuration方式建立仿真网络拓扑。其中源节点采用Possion PMF函数得到按泊松分布产生的DP数据包输入流量,数据包长度服从64 Byte~3 036 Byte的均匀分布,保护带时间为5 μs,最大负载为100 000 bit/s;工作站节点(服务器)数量分别设置为3和10,工作站节点模型均相同,到达每个工作站节点的DP数据包采用Exponential PDF函数得到前后到达时间分布Pt(x)和包大小分布Pp(x)的指数分布业务流和采用niform PDF函数得到前后到达时间分布Pt(x)和包大小分布Pp(x)的均匀分布业务流,且按先进先出(FIFO)的方式存于工作站节点处理器的模块存储器中,仿真时间设置为60 s。由于是基于包的仿真机制,因此采用背景业务能加速仿真运行速度。
5.2 仿真结果及分析
对本文提出的MOR算法和现有主要路由算法的性能进行仿真比较,性能指标为数据包的平均延迟。用于比较的现有主要路由算法包括等负荷大小间隔任务分配(Size Interval Task Assignment With Equal Load,SITA-E)算法、最短期望延迟(Shortest Expected Delay,SED)算法(等价于JSD)、贪婪吞吐量(GT)算法。分别对服务器数量为3和10,Pt(x),Pp(x)为指数和均匀分布的仿真结果如图2所示。

图2 MOR算法与现有路由算法的性能比较
从图2可见,MOR是最优的,JSD是次优的。MOR的平均包延迟在Pt(x)=Pp(x)=Pe(x;1)且p=3、Pt(x)=Pp(x)=Pe(x;1),p=10和Pt(x)=Pp(x)=Pu(x;1)且p=3,Pt(x)=Pp(x)=Pu(x;1)且p=10的情况下比SITA-E和GT的平均包延迟都要小得多,且随着流量强度的增加,平均包延迟减
少得更多,这对负荷流量日益加大的并行处理系统来说无疑节约了传输时间而相应地提高了处理速度;从图2还可看到,在重负荷条件下,所有算法的性能都将随p的减小而提高,这除了与算法本身因素有关外,还与处理器速度和通信链路的带宽等因素有关,后者不属于本文研究的内容。
6 结束语
本文提出一种模拟最佳路由(MOR)算法,该算可工作于任意数量的同类服务器。在目前应用的大多数互联网中,如文件传输和基于IP的语音在一个会话内的所有IP包(除最后传输的包外)大小相同。因此,考虑在一个会话内的IP包大小是不变的。当流量很大且发生突变时,可以把MOR扩展成自适应MOR。自适应MOR从输入流量中获得统计值,并能在前后到达时间或包大小分布变化后作出响应,下一步将对以下3个方面加以研究:(1)α的近似值的计算;(2)权值函数的动态选择,它基于近似包大小的分布;(3)包大小分布的有效近似值,如包大小区间[0,L]的动态选择。
[1]崔梦天,赵海军,李明东,等.基于智能化分配算法的计算机负荷并行处理技术[J].系统工程与电子技术, 2005,30(11):2270-2273.
[2]吴华鑫.分布式服务网络中保证QoS的服务路由算法研究[D].合肥:中国科学技术大学,2009.
[3]左朝树,刘心松,邱元杰,等.分布式并行服务器的动态重构容错算法[J].系统工程与电子技术,2005, 27(5):900-913.
[4]Pavone M,Frazzoli E,Bullo F.A Daptive and Distributed Algorithms for Vehicle Routing in a Stochastic and Dynamic Environment[J].IEEE Transactions on Automatic Control,2011,56(6):1259-1274.
[5]Mohammad S B.The Effect of Heavy-tailed Distribution onthePerformanceofNon-contiguousAllocation Strategies in 2D Mesh Connected Multi-computers[C]// Proceedings of IEEE International Symposium on Parallel& Distributed Processing.Washington D.C.,USA:IEEE Press,2009:1-8.
[6]Oida K,Shinjo K.Characteristics of Deterministic Optimal Routing for a Simple Traffic Control Problem[C]// Proceedings of IEEE IPCCC’99.Washington D.C.,USA: IEEE Press,1999:386-392.
[7]Shenker S,WeinribA.TheOptimalControlof Heterogeneous Queueing Systems:A Paradigm for Load-SharingandRouting[J].IEEETransactionson Computers,1989,38(12):1724-1735.
[8]Crovella M E.PerformanceEvaluationwithHeavy Tailed Distributions[C]//Proceedingsofthe7th JSSPP’01.Cambridge,USA:[s.n.],2221:1-10.
[9]Oida K,ShinjoK.CharacteristicsofDeterministic OptimalRoutingforTwoHeterogeneousParallel Servers[J].InternationalJournalofFoundationsof Computer Science,2001,12(6):775-790.
[10]Shenker S,WeinribA.TheOptimalControlof Heterogeneous Queueing Systems:A Paradigm for Loadsharing andRouting[J].IEEETransactionson Computers,1989,38(12):1724-1735.
[11]Matteo S,Ilaria V.Branch and Price for the Vehicle Routing Problem with Discrete Split Deliveries and Time Windows[J].EuropeanJournalofOperational Research,2011,213(3):470-477.
[12]Christophe D,PhilippeL,CarolineP.Efficient Frameworks for Greedy Split and New Depth First Search Split Procedures for Routing Problems[J].Computers&OperationsResearch,2011,38(4): 723-739.
[13]Nguyen N C,Thanh V D.Optimal Routing Algorithms for Hyper-de Bruijn Networks[C]//Proceedings of ATC’10.Washington D.C.,USA:IEEE Press,2010: 297-300.
[14]Banawan S A,Zahorjan J.Load Sharing in Heterogeneous Queueing Systems[C]//Proceedings of IEEE INFOCOM’89.Washington D.C.,USA:IEEE Press, 1989:731-739.
编辑 索书志
Optimal Routing Policy Based on Multivariable Decision Function
ZHAO Haijun1,LI Min2,LI Mingdong1,YUE Miao1
(1.School of Computer,China-West Normal University,Nanchong 637009,China;
2.Information Communications Branch,Chengdu Power Supply Company,Chengdu 610000,China)
Aiming at the disadvantage of existing routing algorithm in distributed parallel processing system,a novel and effective routing policy is proposed.The concrete implement is to obtain the packet fore-and-aft arriving time distributionPt(x)and the packet size distributionPp(x)from input packets,and a weight function is introduced to achieve the minimal average delay of all packets by learning continuously average fore-and-aft arriving time,average packet size and vector.Simulation result shows that the minimal average delay of all packets can be obtained not only in the condition of the varied number of processors,but also in the condition of the changed packet fore-and-aft arriving time and the packet size distribution.
distributed parallel processing system;multivariable;routing policy;average delay;minimum;flow intensity
赵海军,李 敏,李明东,等.基于多变量判决函数的最优化路由策略[J].计算机工程,2015,41(3):92-96.
英文引用格式:Zhao Haijun,Li Min,Li Mingdong,et al.Optimal Routing Policy Based on Multivariable Decision Function[J].Computer Engineering,2015,41(3):92-96.
1000-3428(2015)03-0092-05
:A
:TN915.6
10.3969/j.issn.1000-3428.2015.03.017
四川省教育厅自然科学基金资助项目(10ZC012);西华师范大学基本科研业务费专项基金资助项目(14C002)。
赵海军(1966-),男,教授,主研方向:无线通信,网络数据通信;李 敏,工程师、硕士;李明东,教授;岳 淼,讲师、硕士。
2014-03-13
:2014-05-21E-mail:zhaohai_jun@163.com

