AVA资料处理方法探讨

刘 冰

（中国石油化工股份有限公司上海海洋油气分公司研究院，上海 200120）

AVA资料处理方法探讨

刘 冰

（中国石油化工股份有限公司上海海洋油气分公司研究院，上海 200120）

摘 要：AVA技术是油气预测中应用较广、准确率较高的方法之一。此文主要介绍了AVA角度道集的处理方法和国内外常用算法，并结合实际钻井钻前AVA预测和钻后油气层特征进行了比较分析。多年的实际AVA应用表明，在选取合适窗口和方法的条件下，AVA预测结果是可靠的。

关键词：AVA; Zeoppritz；角道集；钻前预测

Discussion on AVA Data Processing Methods

LIU Bing

(Institute of SINOPEC Shanghai Offshore Oil and Gas Company, Shanghai 200120, China)

Abstract:AVA method is one of the most useful and accuracy methods in hydrocarbon prediction. The angle stack processing method and common calculation methods at domestic and overseas are mainly discussed in this paper. Combined with the actual drilling data before AVA prediction and after drilling were compared and analyzed. After years of practical application, under the appropriate windows and methods, the results of AVA prediction reliable.

Keywords:AVA; Zeoppritz; angle stacks; prediction before drilling

Shuey通过对Zoeppritz方程的简化[1]，使得AVA技术在实际生产中得到了广泛的应用。本文主要利用叠前地震道集转化成角度道集，针对处理过程中遇到的关键问题进行讨论。

在西湖地区，有早期（1983年）的24次覆盖的地震道集，也有新近（2013年）采集的120次覆盖地震道集；既有直井AVA处理，也有斜井AVA处理。通过钻前预测与钻后含油气层及岩心取样对比，验证了AVA技术的可靠性，并为今后的工作提供有价值的参考。本文的地震角道集处理使用了CGG处理软件的ANGLE模块。

1　叠前道集的预处理

在做AVA资料处理前，通常需要对叠前道集进行一些预处理，比如速度要求远道畸变的道集处理、反动校正用到的密点速度。此外，还有直井和斜井的不同处理方式，弯曲射线路径还是直射线路径等，下面我们就这些情况分别进行讨论。

1.1 对于速度的要求

为了尽可能准确地将道集数据转换为角度道集，需要对校平的道集进行反动校正，对单点进行加密提取叠加速度。需要注意的是反动校正的速度必须和原动较时的速度一致，否则会影响到反动校道集、角度道集的效果和由此提取时深关系的准确性。

1.2 对于远道畸变的处理

对于叠前道集，在做反动校正的时候，有的时候会遇到远道畸变很严重的道集，这个时候我们需要对远道进行切除，但这里需要注意，由于

AVA道集的大角度信息主要利用的是远道道集（图1），在做切除的时候我们需要格外小心，在实际工作中，我们总结的经验是对于浅层畸变可以切除的多一些，深层畸变建议保留，这样可以既保证道集质量，又最大限度的保留大角度信息，以满足AVA反演的要求。但是，多年AVA资料应用表明，30°以内的角道集信息可信度较高。

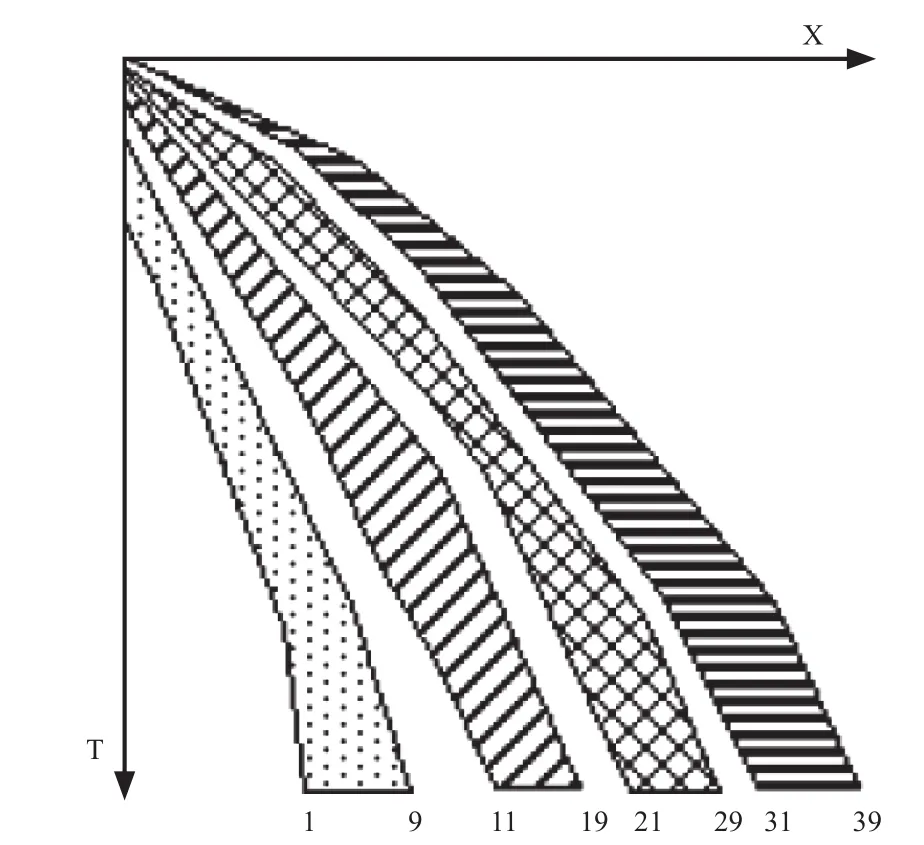
图1　角道集上各角度在道集上的分布

1.3 直井和斜井的处理方式

直井AVA角道集处理通常选取靶点附近左右若干个CDP，具体可视实际情况而定。

实际生产中，经常能遇到斜井的处理情况，这时候靶点的选择通常是沿井轨迹和地层变化特征选择靶点，然后依次按直井的处理方式连接起来。

1.4 弯曲射线与直射线路径选择

在CGG软件里，有弯曲射线路径和直射线路径两种选择方式，实际使用效果和钻井结果对比表明：采用弯曲射线路径处理的含油气层AVA异常特征更清楚，见图2，显示了弯曲射线随振幅变化规律特征明显。该图为东海某井P9含气水层，深度3 707～3 724 m，时间2 725～2 735 ms。

2　常用的算法

Shuey的近似表达式提供了反射振幅随入射角正弦函数的平方的线性表达式：

道集数据是以入射角正弦的平方x和反射振幅y成对出现的。这些点形成集合{(xi, yi), i=1,2, ... , N}，其中N是处理中所有数据的集合。因此，AVO模型可以表示为：

其中我们用Shuey公式的前两项a和b分别表示AVO的截距和梯度。这里 ei对应数据中的误差。预测的 y(xi)值并非实际观测到的yi，我们建立的模型和实际数据只有当ei为零时才成立。线性模型的剩余误差可以表示为：

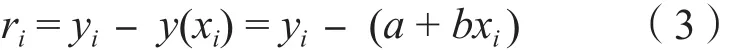
其中ri应该等于ei。我们定义包含a和b的优化函数为 M(a , b)。

2.1 最小二乘法（L2范数）

模型和观测数据的最小平方差可以表述为：

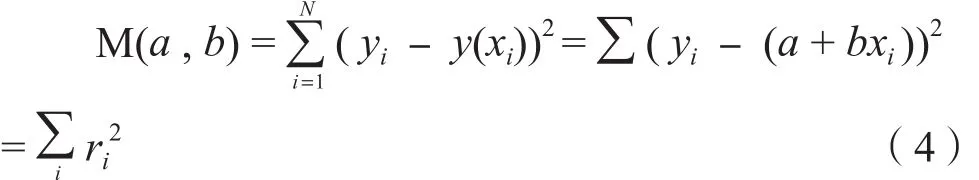
图2　弯曲射线和直射线角度道集（左图为弯曲射线，右图直射线）

通过假设M(a , b)中的a和b为零的偏导数，

可以得到最小化的 M(a , b)[2]。其中 ，

该方法在AVO计算中可以分别估计初始数据的截距 ainit和梯度 binit，并且可用于计算剩余量 ri，进一步可用于估算与初始直线的相似度 σ，其中

2.2 L1模法

在此法中，模型和观测数据的最小平方差可以表述为：

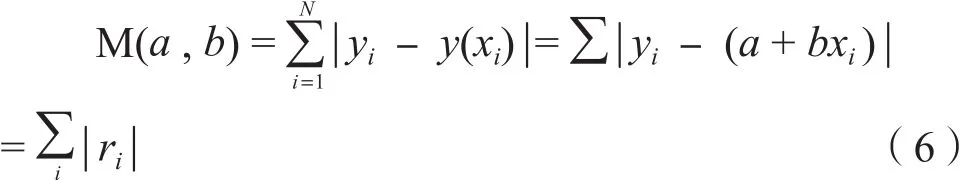
在这个表达式中，找到合适的a和b使M(a , b)的值最小要比最小二乘法难一些[3]，但是如果设定两点就很容易得到，首先，对于设定的b，使 M(a , b)最小的a值为：

对于b的最小化条件，零的偏微分可以表述为：

该方法可从整体数据中根据最小二乘法分别得到初始截距a0和梯度b0，从式（7）中估计出截距a1，从式（8）中估计出梯度b1，重复计算式（7）和式（8）直至得到的精度被控制在0.4%以内。

2.3 Tir中值法

在此法中，没有模型函数，此法的策略是把数据分成三组，每一部分包含相同的数据[4]，此三等分数据被排序在入射角的平方值xi上：对于每组数据（L，M和R），计算x值的中值：

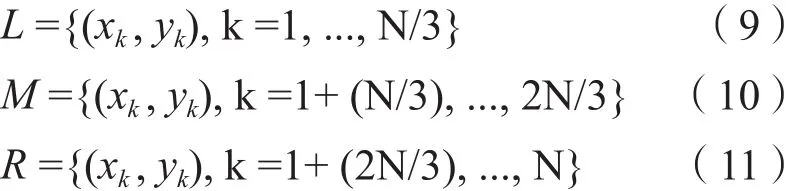
该法可以总结为：对初始数据分成三等分数据，分别计算每组的xi和yi的中值，利用三组 (x, y)估算截距和梯度，其中利用最小二乘法得出最佳的a 和b。

2.4 鲁棒统计法

此法的优化方程是一个加权的最小二乘优化函数，可以表述为：

此法可总结为：首先利用二元中值法得到ainit和binit，利用初始值计算剩余量ri，这些剩余量可用来估算离散度σ，加权的最小平方值可用来分别计算最终的截距afin和梯度bfin。

2.5 时窗AVA法

Ratcliffe和Adler[6]提出一种新的AVA法以改善当相位和振幅随偏移距没变化时的分析法。该法利用反射函数卷积的道集数据的冗余量随不同时间样本的变化量。此法的优化方程可表征为：

其中mji是AVO模型， dji是道集数据关于时间j和偏移距i的函数。

该法可用以估算：①CMP道集中的相位，②地震数据可表述为零偏移距数据sj的卷积模型，则AVO的反映可表述为：

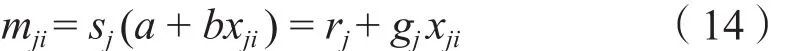
该法可总结为：在时窗中的振幅可叠加为近道（0～10），远道（20～30）和全道（0～30），叠加时窗中的最大能量被用于分析时窗中的子波；需要的子波加权值用于计算最小二乘中的A和B；该分析循环执行到下一个时间样本直至得到设定的误差范围内。

3　 钻前AVA预测与钻后含油气层岩心取样对比

由图3可见，该井钻遇4套明显的含气水层，均有含气后AVO异常显示。其中，第一处含气水层厚度29.6 m，孔隙度10%、泥质质量分数10%，物性较好，钻前预测与实钻结果基本一致；第二处含气水层厚度7.6 m，孔隙度11.3%、泥质质量分数8.3%，物性较好，钻前未预测，但角道集上略有弱显示；第三处含气水层厚度40.1 m，孔隙度9.7%、泥质质量分数11%，物性较好，钻前预测与实钻结果基本一致；第四处含气水层厚度12.2 m，孔隙度9.7%、泥质质量分数4.7%，物性较好，钻前预测与实钻结果基本一致。

显而易见，对处理较好的AVA资料而言，只要含油气层厚度较厚、且物性较好时，角道集上有可能呈现含油气后的AVA异常显示。

4　结论

（1）在对较平的道集进行反动校正时，需使用原动校正的速度，否则会产生误差；

（2）多年的AVA实际应用表明，30°以内的角度道集信息可信度较高；

（3）在AVA资料处理中，采用弯曲射线计算方法比直射线计算方法更能显示含油气层AVA异常特征。

图3　东海某井钻前AVA预测与钻后含油气层岩心取样对比

参考文献：

[1]SHUEY R T. A Simplification of the Zoeppritz Equations[J]. Geophysics， 1985（50）: 609-614.

[2]DRAPER N R， SMITH H. Applied Regression Analysis[M]. John Wiley & Sons， 2ndedition， 1981.

[3]PRESS W H， TEUKOLSKY S A， VETTERLING W T， et al. Numerical Recipes in FORTRAN: The Art of Scientific Computing[M]. Cambridge University Press， 2ndedition， 1992.

[4]ANDREWS D F. A Robust Method for Multiple Linear Regression[J]. Technometrics， 1974（16）: 523-531.

[5]WALDEN A T. Making AVO Sections More Robust[J]. Geophys. Prosp.， 1991: 915-942.

[6]RATCLIFFE A， ADLER F. Accurate velocity analysis for Class II AVO events[C]， 70th SEG annual conference， expanded abstracts， 2000.

作者简介：刘冰，男，1983年生，硕士，主要从事地震资料处理和储层预测工作。E-mail: liubing.shhy@sinopec.com。

收稿日期：2014-09-01；改回日期：2014-11-28

文章编号：1008-2336（2015）01-0032-04

中图分类号：P631.4+43

文献标识码：A DOI:10.3969/j.issn.1008-2336.2015.01.032