RTK在南水北调中线工程顶管贯通中的应用

王铁生, 李广静, 高亚伟, 冯　康

(1.华北水利水电大学,河南 郑州 450045; 2.郑州瑞龙混凝土有限公司,河南 郑州 450000)



RTK在南水北调中线工程顶管贯通中的应用

王铁生1, 李广静1, 高亚伟2, 冯康1

(1.华北水利水电大学,河南 郑州 450045; 2.郑州瑞龙混凝土有限公司,河南 郑州 450000)

摘要：针对顶管技术无需开挖的施工特点,结合南水北调中线工程焦作段某顶管贯通工程的具体实例,提出了RTK测量应用于短距离顶管贯通的方法.对比分析了导线测量、三角网测量、RTK测量3种方法在顶管贯通过程中的测量精度水平,用导线法和权函数法来计算贯通误差.计算结果表明:RTK测量技术完全满足该顶管贯通工程的精度要求,在短距离顶管贯通工程中可以代替导线测量和三角网测量建立顶管贯通测量控制网,并且其具有速度快、受地形条件影响小的特点,在短距离顶管贯通中具有较好的适用性.

关键词：南水北调中线工程；顶管贯通;RTK;精度水平;导线法;权函数法

顶管法施工技术是非开挖铺设地下管道的施工技术.其借助主顶油缸及管道间、中继间等的顶推力,把工具管或掘进机从工作井内穿过土层一直推到接收井内吊起，管道紧随工具管或掘进机后埋设在工作井与接收井之间[1-2].顶管贯通测量技术中存在横向、竖向和纵向误差[3].竖向误差的影响规律比较简单,纵向误差并不直接影响顶管的贯通,而横向误差直接影响顶管贯通的效果,是贯通误差预计计算的控制指标[3-4].

横向贯通误差的来源包括洞外地面控制测量的误差、联系测量的误差、洞内导线测量的误差以及施工误差[4].其中,施工误差可以忽略不计，在仅有一个贯通面的情况下不存在联系测量[4-5]，常规情况下地面控制测量误差比较容易满足要求，因此,减小洞内导线测量的误差是测量人员的主要任务.顶管贯通测量中常用的方法有导线测量、三角网测量[6-7].但是在本次的焦作段顶管贯通实例中，由于地下管线短且比较简单,故洞内测量误差比较容易控制.在洞外地面控制测量的过程中，由于顶管入口处至顶管出口处只有一条狭长的区域，且顶管需要穿越车流量大的省道,严重影响了通视观测，使导线测量、三角网测量均受到限制.而RTK(Real-time Kinematic)测量是一种能够在野外实时得到厘米级定位精度的测量方法，因此提出了用RTK的方法进行顶管贯通测量.

1地面控制网常用方法

1.1　导线网

导线网的布设可分为闭合导线、附合导线及支导线.导线测量容易克服地形障碍,布设灵活,可单线推进,精度均匀.缺点是结构强度低,几何条件少,测边工作量大[6].

1.2　三角网

三角网是在地面选取一系列控制点,分成若干相互连接的三角形,构成各种网或锁状图形[7].观测三角形的内角或边长,再根据已知控制点的坐标方位角、坐标和起始边边长解算得到各边的边长和坐标方位角,然后待定点的平面坐标可由直角坐标正算公式计算.三角网测量对测边要求很高,易受地形影响,平差工作量大.

1.3　RTK及GPS测量

GPS作为新兴的测量技术,具有速度快、全天候、劳动强度低、数据解算精度高、受外界环境影响较小、布网范围大等优点.如图1所示，在顶管的贯通过程中,GPS控制网的布网设计应满足:洞口至少应设置3个控制点作为顶管施工各开挖口的控制点;每个点至少连接3条边;GPS定位点之间如J1和C1一般不要求通视,但点位四周高度角15°以上,无成片障碍物,以保证GPS信号接收；为削弱垂线偏差,同一洞口处的3个控制点尽量位于同一高程,各洞口控制点之间的高差尽量小一些[8-9].

图1　顶管洞外GPS平面控制网布设示意图

在短距离单向顶进贯通工程中常用RTK测量方法直接测量单点坐标.顶管附近至少要布设3个平面控制点,点位稳定,便于到达和使用.对于直线顶管,应在进、出口的定测中线上布设2个控制点,另外再布设2个与洞口点通视的定向点.天线应采用三角支架架设,仪器的圆气泡应稳定居中.RTK观测前设置的平面收敛阈值不应超过2 cm,垂直收敛阈值不应超过3 cm.

2贯通误差计算方法

2.1　导线法

导线法是一种近似估算方法[9].用地面三角形网、导线网作洞外平面控制时,选择最靠近顶管中线的一条线路作为导线,用下列导线公式估算对横向贯通误差的影响值.

(1)

2.2　权函数法

估算顶管横向贯通误差影响值的原理[10]如下.设顶管洞外平面控制网及坐标轴、顶管轴线如图2所示.从进口点J和定向点A,经过洞内导线推算出贯通点G的坐标;从出口点C和定向点B,经洞内导线推得贯通点G的坐标.把βJ,βC,SJG,SCG看作不含误差的量,由图2可知,顶管洞外平面控制测量误差影响值即为贯通点G的横坐标差ΔYG的中误差.

d(ΔYG)=aJAΔXJGdXJ+(1+bJAΔXJG)dYJ-

aJAΔXJGdXA-bJAΔXJGdYA-

aCBΔXCGdXC-(1+bCBΔXCG)dYC+

aCBΔXCGdXB+bCBΔXCGdYB,

(2)

式(2)为贯通点的横坐标差权函数式.由式(2)可知,在给定的顶管独立坐标系下,G洞外平面控制网影响值与进口点J、出口点C及相应定向点A和B的位置、精度以及贯通点G的位置有关.

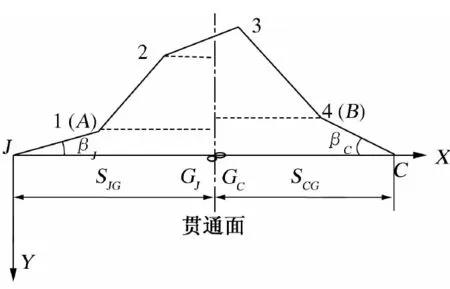
图2　横向贯通误差影响值估算示意图

3工程实例

该顶管贯通工程位于南水北调中线工程焦作段,起止桩号为WZ23+350—WZ23+490,全长140 m.该顶管需穿越某省道进行贯通,原始方案为单向贯通,由于当地地质条件较为复杂,管道顶进至57 m时无法继续顶进,必须重新设计对向顶进路线.由于贯通点的位置处于公路下方,无法进行开挖,增大了贯通的难度,需要设计较高精度的施工方案确保顶管顺利贯通.管道穿越的省道车流量较大，且受道路两旁建筑物的影响,贯通的入口点与出口点间只有一狭窄的胡同可以进行测站传递,加大了布设导线网的难度.针对现场情况,分别利用3种测量方法建立顶管贯通测量的控制网,并对比3种方法的精度水平,分析不同方法对贯通误差的影响.

1)导线网法.闭合导线观测方法如图3所示.

图3　闭合导线观测示意图

以A1为原点，A1A2为X轴方向建立施工平面坐标系.从A1出发逆时针观测最后到A2.在各个观测站上观测3个测回,根据导线观测数据计算出各个点的坐标见表1.

表1　导线计算数据 　m

求得X坐标的增量闭合差[6]为-0.004 m,Y坐标的增量闭合差为-0.001 m.导线全长相对闭合差为1/51 493.根据权函数法计算公式可以计算得出贯通误差为3.476 mm.下述各方法的贯通误差均依据此来计算.

2)三角网法.由于地形条件限制，A6点观测困难,故布设成如图4所示的三角网进行观测.根据观测数据计算得各点的坐标见表2.

图4　三角网观测示意图

表2　三角网计算数据　m

求得X坐标的增量闭合差为0.001 m,Y坐标的增量闭合差为-0.001 m.导线全长相对闭合差为1/223 895.计算贯通误差为3.096 mm.

3)RTK法.使用仪器型号为Leica GPS1200,标称水平精度为10 mm+1 ppm[11].根据布设的导线网和三角网，分别依次观测各点的坐标,坐标数据分别见表3和表4.

表3　导线网布设图的RTK测量数据 　m

表4　三角网布设图的RTK测量数据 　m

两次观测数据相差较小,且RTK单点观测精度与网形联系较小,因此取两次RTK观测数据的均值作为计算贯通误差的依据.计算得到贯通误差为3.225 mm.

导线网法及RTK法与三角网法各点的坐标差值分别如图5和图6所示.

图5　导线网与三角网数据对比图

图6　RTK与三角网数据对比图

由图5可知：X方向的最大差值为0.013 mm,最小差值为0.000 mm；Y方向最大差值为0.004 mm,最小差值为0.000 mm.由图6可知：X方向的最大差值为0.003 mm,最小差值为0.000 mm；Y方向的最大差值为0.002 mm，最小差值为0.000 mm.由此可知,RTK法与三角网法的数据更接近,导线网法与三角网法的数据差距较大.

采用不同的测量方法，得出的贯通误差如下:导线网法的贯通误差为3.5 mm,三角网法的贯通误差为3.1 mm,RTK法的贯通误差为3.2 mm.

该顶管贯通工程精度要求为5 mm,由此可以得出以下结论:①通过对比，3种方法都满足贯通精度要求;②三角网法所得贯通误差最小,RTK法次之,传统导线网法最差,但RTK法与导线网法的贯通误差相差很小,精度基本相同;③三角网法精度高但观测方法繁琐,导线网法简单但精度较低,RTK法速度快且精度适中.

4结语

结合工程实例，研究了RTK技术用于建立顶管贯通测量控制网的可行性和精度水平，得出以下结论:①在短距离的顶管贯通工程中,RTK测量的精度可以满足工程的需要;②在外界环境及地形条件不利的情况下，该方法可以快速地求得顶管贯通的误差;③在已有顶管贯通测量控制网时,可利用该方法进行控制网的精度检验和复测工作.

导线网法、三角网法和RTK法均可满足施工精度的要求,但是RTK法速度快,受地形条件限制小,工作量较小.综合考虑，RTK测量具有一定的优势.

参考文献

[1]余彬泉,陈传灿.顶管施工技术[M].北京:人民交通出版社,1998.

[2]吴修锋.顶管施工引起的地层移动与变形控制研究[D].南京:南京工业大学,2004.

[3]杜传鹏.长大隧道贯通误差分析及程序实现[D].成都：西南交通大学,2010.

[4]张正禄.工程测量学[M].武汉:武汉大学出版社,2005.

[5]张正禄.隧道施工地面导线网的合理布设[J].武汉测绘学院学报,1982(1):7-15.

[6]张正禄,张松林,伍志刚,等.20～50 km超长隧道(洞)横向贯通误差影响值研究[J].测绘学报,2004，33(1)：83-88.

[7]姜宏艳,刘勇.浅谈地下顶管施工测量[J].黑龙江交通科技,2010(2)：53-54.

[8]瞿静庵,王景.GPS控制网在大连南山隧道测量中的应用[J].民营科技,2010(6):209.

[9]徐绍铨,张华海,杨志强,等.GPS测量原理及应用[M]. 武汉:武汉大学出版社,2003.

[10]路伯祥,陶国冶.隧道导线网测量误差对贯通误差影响值的严密估算方法[J].铁道学报,1989,2(11):59-63.

[11]于来法.地下铁道地面控制网布设方案和测量精度设计[J].测绘通报,1996(6):11-13.

(责任编辑：陈海涛)

Application Research on RTK in the Traversing Engineering of Pipe Jacking in the Middle Route Project of South to North Water Diversion

WANG Tiesheng1, LI Guangjing1, GAO Yawei2, FENG Kang1

(1.North China University of Water Resources and Electric Power, Zhengzhou 450045, China;

2.Zhengzhou Dragon Concrete Co., Ltd., Zhengzhou 450000, China)

Abstract:Considering the features of pipe jacking technology with no excavation, and combining with the example of the traversing engineering of a pipe jacking in Jiaozuo section in the Middle Route Project of South to North Water Diversion, we proposed a method that applied RTK measure technology to the short-distance traversing engineering of pipe jacking, the precision levels of three measure methods applied to traversing of pipe jacking were comparatively analyzed, three methods were traverse survey, triangulation measure, RTK measure, and the traversing errors were calculated by traverse survey and weight functions. The computing results show that RTK measure technology completely satisfies the precision requirements of traversing engineering of pipe jacking project. In the short-distance traversing engineering of pipe jacking, this technology can replace the traverse survey and triangulation measure with the surveying control network of traversing engineering of pipe jacking, and has the characteristics of fast speed and little influences from terrain conditions. Thus, RTK measure technology has better applicability in the short-distance traversing engineering of pipe jacking project.

Keywords:the Middle Route Project of South to North Water Diversion; traversing of pipe jacking; RTK; precision level; traverse method; weight function

中图分类号：TV67；TB22

文献标识码：B

文章编号：1002-5634(2015)02-0040-04

DOI:10.3969/j.issn.1002-5634.2015.02.009

作者简介：王铁生(1966—),男,河北定州人,教授,博士,主要从事工程测量及GPS数据处理方面的研究.

基金项目:国家自然科学基金项目(41101373).

收稿日期:2014-11-04