基于萤火虫算法的集装箱码头集卡路径多目标优化研究

卓宏明

(浙江国际海运职业技术学院，浙江　舟山　316021)

基于萤火虫算法的集装箱码头集卡路径多目标优化研究

卓宏明

(浙江国际海运职业技术学院，浙江舟山316021)

摘要:在两艘船同时作业情况下，建立以集卡总行驶距离最短及完成两船所有装卸任务的时段内各箱区间作业量不平衡性最小的多目标优化模型。在模型求解时，采用新颖的萤火虫算法求解，编码方式采用离散整数编码，每个整数编码表示对应的集卡作业回路运行次数。最后通过舟山甬舟集装箱码头案例分析，较好的解决了集卡路径优化问题，为码头运营者提供了一定的决策支持，也验证了模型与算法的有效性与实用性。

关键词:集装箱码头；集卡调度；萤火虫算法

0引言

随着集装箱码头业务竞争的日益激烈，如何在现有规模下提高码头资源利用率,提高集装箱码头运作效率，就必须合理解决集卡调度问题。NISHIMURA (2005)[1]建立了集卡动态路径优化模型，并比较分析集卡静态调度与动态调度，最后用遗传算法求解模型。Lai Ming yong、Cao Erbao(2010)[2]建立了以车辆行走距离总和最小的混合整数规划模型，并采用自适应遗传算法对该模型进行求解；杨静蕾(2006)[3]建立了以集卡总行程最短为目标的集卡调度模型；计明军、刘丰硕等(2010)[4]建立了基于作业面的两船装卸协同作业的集装箱码头集卡调度；赵斐(2011)[5]建立了面向“作业面”的集装箱码头集卡路径成本优化模型，并用遗传算法混合蚁群算法求解模型；陆永祥(2013)[6]研究了在“作业面”调度模式下的集装箱码头集卡调度以及集卡合理配置。但多数文献只考虑了单目标没有考虑箱区间的作业量平衡问题。

本文在码头现行的“作业面”集卡调度作业基础上，研究两船同步装卸作业，提出完成两船所有装卸的集卡总行驶距离最短和该作业时段内各箱区的作业量不平衡性最小的多目标集卡调度优化模型。

1多目标集卡路径优化模型

1.1问题描述

当集装箱船舶靠泊后，两艘船舶进行同步装卸，如何确定集卡的作业回路，使得完成所有装卸作业的集卡总行驶路程最短，并且该作业时段内各箱区的作业量不平衡性最小。进口箱区的作业量包括进口箱量和外部集卡的提箱箱量，而出口箱区的作业量包括出口箱量和外部集卡的集港箱量，从而降低堆场交通阻塞，提高集装箱码头的作业效率，降低生产作业成本。

1.2模型的假设

模型基于以下几点假设：本论文的主要研究对象是单挂集卡每次仅运输一个集装箱；码头各节点之间的集卡行驶距离已知；集装箱码头堆场采用进出口箱分开堆存策略；船舶在集装箱码头进、出口箱量已知；实际码头装船前，A1/A2/A3/B1/B2/B3等出口箱区的出口箱量已确定；开始作业前箱区中所在的箱量及箱区的容量已知；作业时段内外卡在各箱区的提箱量、集箱量已知。A4/A5为a船舶的进口箱区，B4/B5为b船舶的进口箱区。

1.3集卡模型的建立

模型符号说明:YIa表示a船所在泊位分配的进口箱区总数；YIb表示b船所在泊位分配的进口箱区总数；YQa表示a船所在泊位分配的出口箱区总数；YOb表示b船所在泊位分配的出口箱区总数；ai表示a船所在泊位分配的第j个进口箱区，ai=1，2，3，…，YIa；bi表示b船所在泊位分配的第i个进口箱区，bi=1，2，3，…，YIb；aj表示a船所在泊位分配的第i个出口箱区，aj=1，2，3，…，YQa；bj表示b船所在泊位分配的第j个出口箱区，bj=1，2，3，…，YQb；Lai表示集卡在卸箱船舶a进口作业回路，卸箱船舶a→进口箱区ai→卸箱船舶a行走一圈的距离；Lbi表示集卡在卸箱船舶b进口作业回路，卸箱船舶b→进口箱区bi→卸箱船舶b行走一圈的距离；Laibj表示集卡在卸箱a船舶、装箱船舶b，两船同步装卸作业回路，卸箱船舶a→进口箱区ai→出口箱区bj→装箱船舶b→卸箱船舶a行走一圈的距离，且a≠b；Lbiaj表示集卡在卸箱船舶b、装箱船舶a，两船同步装卸作业回路，卸箱船舶b→进口箱区bi→出口箱区aj→装箱船舶a→卸箱船舶b行走一圈的距离，且a≠b；Laj表示集卡在装箱船舶a出口作业回路，装箱船舶a→出口箱区aj→装箱船舶a行走一圈的距离；Lbj：表示集卡在装箱船舶b出口作业回路，装箱船舶b→出口箱区bi→装箱船舶b行走一圈的距离；Iai：表示作业时段内a船所在泊位分配的第ai个进口箱区的总作业量；Ibi：表示作业时段内b船所在泊位分配的第bi个进口箱区的总作业量；Qaj表示作业时段内a船所在泊位分配的第aj个出口箱区的总作业量；Obj表示作业时段内b船所在泊位分配的第bj个出口箱区的总作业量；Qai表示a船所在泊位分配的第ai个进口箱区的总容量；Qbi表示b船所在泊位分配的第bi个进口箱区的总容量；Qaj表示a船所在泊位分配的第aj个出口箱区的总容量；Qbj表示b船所在泊位分配的第bj个出口箱区的总容量；Nai表示船舶a的进口总箱量；Nbj表示船舶b的进口总箱量；Naj表示船舶a的出口总箱量；Nbj表示船舶b的出口总箱量；yai表示作业时段内a船所在泊位分配的第ai个进口箱区的外卡总提箱量；ybi表示作业时段内b船所在泊位分配的第bi个进口箱区的外卡总提箱量；yaj表示作业时段内a船所在泊位分配的第aj个出口箱区的外卡总集箱量；ybj表示作业时段内b船所在泊位分配的第bj个出口箱区的外卡总集箱量；

决策变量:xai决策变量,表示集卡在卸箱船舶a进口作业回路，卸箱船舶a→进口箱区→ai卸箱船舶a的行走次数；xbi决策变量,表示集卡在卸箱船舶b进口作业回路，卸箱船舶b→进口箱区bi→卸箱船舶b的行走次数；xaibj决策变量,表示集卡在卸箱船舶a、装箱船舶b，两船同步装卸作业回路，卸箱船舶a→进口箱区ai→出口箱区bj→装箱船舶b→卸箱船舶a的行走次数，且a≠b；xbiaj决策变量,表示集卡在卸箱船舶b、装箱船舶a，两船同步装卸作业回路，卸箱船舶b→进口箱区bi→出口箱区aj→装箱船舶a→卸箱船舶b的行走次数，且a≠b；xaj决策变量,表示集卡在装箱船舶a出口作业回路，装箱船舶a→出口箱区aj→装箱船舶a的行走次数；xbj决策变量,表示集卡在装箱船舶b出口作业回路，装箱船舶b→出口箱区bj→装箱船舶b的行走次数；

路径优化模型以集卡总行程最短及完成两船所有装卸任务的时段内各箱区间作业量不平衡性最小的多优化目标函数。

总目标函数:

f=f1×f2

(1)

目标函数1:

(2)

目标函数2:

f2=min(max(max(Iai+yai)，max(Ibi)，max(Oaj)，max(Obj))-min(min(Iai)，min(Ibi),min(Oaj)，min(Obi)

(3)

约束条件：

Iai=χai+χaibj+yai,Ibi=χbi+biaj+ybi

(4)

Oaj=χai+xbiaj+yai，Obi=χbj+χaibj+ybj

(5)

0≤χai+xaibj-yai≤Qai，0≤χbi+χbiaj-ybi≤Qbi

(6)

0≤-(χaj+χbiaj)+yaj≤Qaj,0≤-(χbj+χaibj)+ybj≤Qbj

(7)

(8)

(9)

0≤χai≤Nai,0≤χbi≤Nbi,0≤χaj≤Naj,0≤χbj≤Nbj

(10)

0≤χaibj≤min(Nai,Nbj),0≤χbiaj≤min(Nbi,Naj)

(11)

χai,χbi,χaibj,χbiaj,χaj,χbj=0,1,2,3…

(12)

其中：

式(1)是以集卡总行程最短及完成两船所有装卸任务的时段内各箱区间作业量不平衡性最小的多优化目标函数；式(2)是目标函数1以集卡总行程最短为优化目标；式(3)是目标函数2以完成两船所有装卸的时段内各箱区间作业量不平衡性最小为优化目标；式(4)和式(5)表示各箱区的总作业量为完成两船所有装卸任务的时段内进口箱量(出口箱量)与外卡提箱量(外卡集箱量)之和；式(6)和式(7)表示各箱区的箱量需要满足的容量约束；式(8)和式(9)保证船舶所有装卸任务的完成；式(10)和式(11)表示决策变量需要满足的进出口箱量约束；式(12)表示决策变量集卡作业回路行走次数为非负整数。

2模型求解

2.1萤火虫算法(FA)

萤火虫算法(FA)由剑桥学者Yang xin-she在2008年提出[7]，自然界中的萤火虫个体用搜索空间中的点模拟，个体吸引和移动过程用搜索和优化过程模拟，萤火虫个体所处位置的好坏，转化为求解问题的目标函数度量，搜索和优化过程中用好的可行解取代较差可行解的迭代过程类比萤火虫个体的优胜劣汰过程。

2.2编码方式

本模型将整靠泊的两艘船舶同步装卸的集卡所有作业回路运行次数作为决策变量。船a与船b集卡调度时，把集卡所有的作业回路运行次数作为一个萤火虫，假设船舶所在泊位分配的进口箱区总数为YIa、出口箱区总数为YOa；船舶a所在泊位分配的进口箱区总数为YIb、出口箱区总数为YOb，则萤火虫求解空间维数为N=YIa+YIb+YIa×YOb+YIb×YOa+YOa+YOb维，矩阵中每个元素就是集卡对应的作业回路运行次数。由于作业回路运行次数为整数，所以采用离散整数编码，每个整数编码表示对应的集卡作业回路运行次数。

2.3算法流程

[编者按] 为深入贯彻落实《中共中央 国务院关于实施乡村振兴战略的意见》(中发〔2018〕1号)和《乡村振兴战略规划(2018-2022年)》，推动乡村旅游提质增效，促进乡村旅游可持续发展，加快形成农业农村发展新动能，文化和旅游部等17部门联合印发了《关于促进乡村旅游可持续发展的指导意见》。现转载如下。

步骤1：初始化算法基本参数。FA算法基本参数的初始化。萤火虫数目n；光吸收强度系数γ；步长因子α；最大吸引度β0；最大迭代次数maxt。

步骤2：在可行区域的范围内随机初始化n个萤火虫位置。

步骤3：计算萤火虫的适应度值，也就是计算目标函数值。

步骤4：用萤火虫的相对萤光亮度公式：

I=I0×e-γrij

(13)

及萤火虫的吸引度公式：

β=β0×e-γr2ij

(14)

其中，I0为萤火虫自身(r=0处)的萤光亮度，称为最大萤光亮度，它与目标函数正相关，目标函数值越优萤火虫亮度就越高。γ为光强吸收系数，通常设为常数，设置光强吸收系数用以体现萤光会随着距离的增加和传播媒介的吸收逐渐减弱。rij为萤火虫i和j之间的空间距离。β0为光源处(r=0处)的吸引度，称为最大吸引度。

步骤5：用萤火虫i被萤火虫j吸引而向其移动的位置更新公式：

χi=χi+β×(χj-χi)+α×(rand-1/2)

(15)

其中，χi、χj为萤火虫i和j所处的空间位置；α为步长因子，是[0，1]区间上的常数；rand为[0，1]区间上服从均匀分布的随机因子。

随机扰动最佳位置的萤火虫，再更新萤火虫的位置并满足约束条件。由于决策变量为非负整数，所以对其移动距离做了放大取整处理。

步骤6：迭代次数加1。判断是否满足最大迭代次数，满足则输出最优值，否则，返回步骤3。

3舟山甬舟集装箱码头案例分析

以舟山甬舟集装箱码头为例进行案例分析。该码头位于浙江省舟山市金塘大浦口，前沿水深-18 m，规划建成5个总长为1 774 m、年吞吐通过能力达250万标箱的现代化大型集装箱泊位。现在已经建成2个泊位及17.5万平方的堆场，2013年吞吐量已经突破50万TEU。查询码头船舶作业计划可知2014年5月12日当天靠泊的联合22船，(为简化船名这里用船a来代替)进口箱量为20 TEU，分配的进口箱区为A4、A5，出口箱量为70 TEU，分配的出口箱区为A1、A2、A3；靠泊的柏安9号船(为简化船名这里用船b来代替)进口箱量为180 TEU分配的进口箱区为B4、B5，出口箱量为121 TEU分配的出口箱区为B1、B2、B3。各箱区的容量及完成两船所有装卸作业时段内的外卡提箱量、集港箱量如表1所示。码头各节点之间的集卡行驶距离如表2所示。该案例的萤火虫求解空间为2+2+2×3+2×3+3+3=22维。

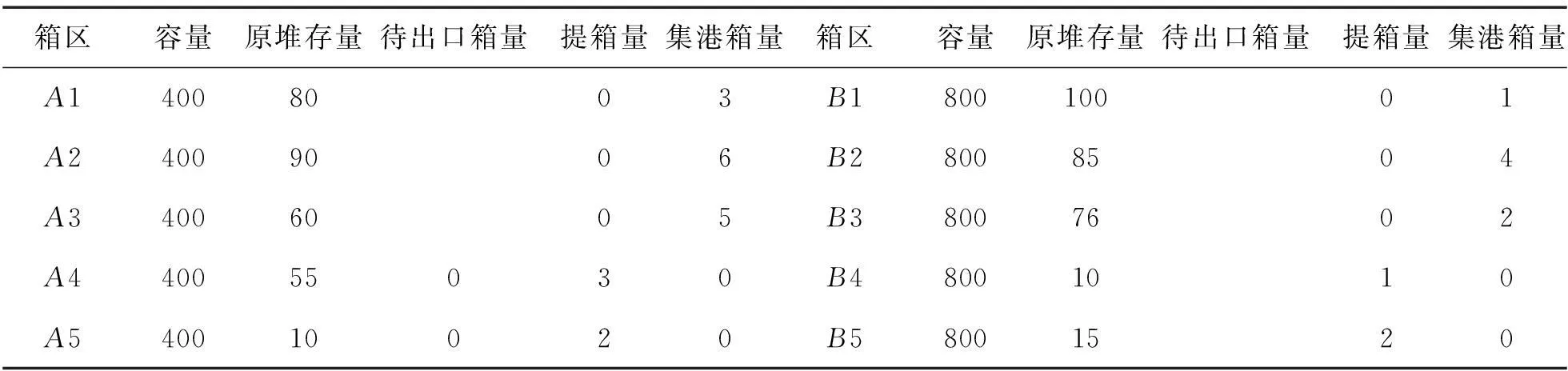
表1　各箱区的容量、原堆存量、提箱集港箱量(TEU)

表2　码头各节点间集卡行驶的距离(m)

FA算法中萤火虫数目取50，光吸收强度系数为1；步长因子为0.2；最大吸引度为1；最大迭代次数为300。模型求解收敛图如图1所示，总目标最优值为3 672 000。目标1集卡总运行距离为459 000m，目标2各箱区作业量极差为80TEU。

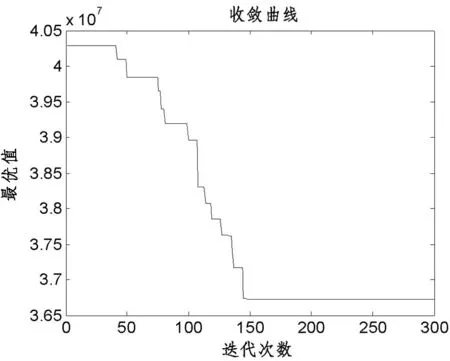
图1　模型最优结果收敛曲线

所求得的最优集卡运输线路和运输箱量如表3所示。

表3　集卡运输线路和运输箱量(TEU)

通过FA萤火虫算法求得模型的解，所得的集卡最优运输线路可以实现集卡的总运输距离及各箱区的作业量不平衡性最小的多优化目标。

4结语

本文提出了面向“作业面”的两船同步装卸的集卡路径优化多目标模型，运用萤火虫算法求解模型，最后通过甬舟码头案例分析，结果表明该方法较好的解决了集卡路径优化问题，为码头运营者提供了一定的决策支持。

参考文献：

[1]NishimuraEtsuko.Yardtrailerroutingatamaritimecontainerterminal[J].TransportationResearchPartE,2005,41(1):53-76.

[2]LaiMingyong,CaoErbao.Animproveddifferentialevolutionalgorithmforvehicleroutingproblemwithsimultaneouspickupsanddeliveriesandtimewindows[J].EngineeringApplicationsofArtificialIntelligence,2010，23(2):188-195．

[3]杨静蕾.集装箱码头物流路径优化研究[J].水运工程,2006，(1):32-35.

[4]计明军,刘丰硕,李郭记,等.基于装卸协同作业的集装箱码头集卡调度及配置优化[J].大连海事大学学报:自然科学版,2010,36(1):47-50.

[5]赵斐.基于GA-ACO的港口集卡路径优化研究[D].邯郸:河北工程大学,2011.

[6]陆永祥.实时作业调度下集卡优化配置数量的确定[D].大连:大连海事大学,2013.

[7]刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011，28(9):3295-3297．

Multi-objective Truck Routing Optimization of Container

Terminals Based on Firefly Algorithm

ZHUO Hong-ming

(Zhejiang International Maritime College, Zhoushan 316021, China)

Abstract:In order to improve the efficiency of container stevedoring, in two boats at the same time operating conditions, the establishment of a set of cards in each box within the shortest total distance traveled and the completion of the task of handling two ships of all time intervals the least amount of work unbalanced multi-objective optimization model. When solving the model, using a novel fireflies algorithm, encoding discrete integer encoding, each integer corresponding to the coded representation of the working circuit card assembly operation times. Finally, Ningbo Zhoushan Container Terminal by case analysis, the results show that the method to solve a set of cards better path optimization problems for terminal operators to provide a certain amount of decision support, meanwhile demonstrate the effectiveness and practicality of the model and algorithms.

Key words:container terminals; truck scheduling; firefly algorithm

浙江交通职业技术学院学报，第16卷第1期，2015年3月

Journal of Zhejiang Institute of Communications

Vol.16 No.1,Mar.2015

作者简介：于文波(1979-)，女，辽宁凌源人,高级实验师,硕士,E-mail:yuwenbobo@126.com。

基金项目：2014年沈阳工程学院学生创新科研项目(LGXS-1404)

收稿日期：2014-11-03

文章编号：1671-234X(2015)01-0033-05

中图分类号:U691.72?

文献标识码：A doi：10.3969/j.issn.1671-234X.2015.01.008