基于顺路原则及位置预估的动态调度策略

曹剑东，李家文

(1.交通运输部 科学研究院，北京 100029；2.浙江工业大学 机械工程学院,杭州 浙江 310014)

基于顺路原则及位置预估的动态调度策略

曹剑东1，李家文2

(1.交通运输部 科学研究院，北京 100029；2.浙江工业大学 机械工程学院,杭州 浙江 310014)

摘要：针对市内货物配送和收集这一典型的集送货问题，在利用“混合禁忌搜索算法”进行静态调度求解的基础上，提出基于“顺路原则”的局部调整策略实现集送货问题的动态调度计算.计算过程中采用模糊推理方法选择局部调整范围，同时采用车辆位置预估方法消除计算、传输和执行延迟带来的车辆位置的变化对优化结果的影响.以40个遍布于北京的客户构成的集送货问题为例，验证了动态调度策略的有效性。

关键词：运输经济；动态调度；顺路原则；模糊推理；集送货

Dynamic dispatch strategy based on by-way principle

and location pre-estimation

CAO Jiandong1, LI Jiawen2

(1.China Academy of Transportation Sciences, Beijing 100029, China;

2.College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:In order to solve the typical problem for urban cargo pickup and delivery, dynamic dispatch calculation is proposed by local adjustment strategy called as “by-way principle”, which is based on static dispatch solutions worked out by hybrid tabu search algorithm. Local adjustment range is selected using fuzzy reasoning method in calculation progress and influence of vehicle location change due to calculation, transmission and performance delay is lessened using pre-estimation method to determine vehicle location. Calculation obtained for a pickup and delivery problem example with 40 customers in Beijing validates the efficiency of dynamic dispatch strategy。

Keywords:transport economy; dynamic dispatch; by-way principle; fuzzy reasoning; pickup and delivery

配送和集货是物流中的一个重要环节，是货物在物流结点与收发货人之间流动的过程[1].对运输车辆的行驶线路进行有效的优化调整，可大幅减少车辆的空驶里程.集送货问题可以分为静态调度和动态调度两类.在静态调度方面，唐俊、杨浩雄、王飞、郑四发[2-6]等采用粒子群算法、蚁群算法和禁忌搜索算法对该问题进行研究并取得不错的效果。

在集送货动态调度方面，其主要的优化策略包括两类，即“重新优化策略”和“局部调整策略”.“重新优化策略”实际上可以看作是动态调度问题的一种静态的求解策略，其计算量大，时效性低，因此不适于实时性要求高的动态调度计算.局部调整与重新优化原理不同，是根据接收到的动态信息对现有行驶路径进行局部改进.Madsen等人[7]提出插入法求解运送老人和残疾人的问题，Gendreau等[8]针对一类比较特殊的信使服务优化调度问题，提出一种适应存储的改进禁忌搜索算法.但是上述算法优化大规模的实际集送货问题时在计算时间和精度方面很难兼顾，另外，算法忽略由于计算、传输和执行的延迟导致车辆位置变化而产生的误差，将进一步降低优化精度.针对集送货动态调度问题，在采用车辆位置预估方法估计车辆当前位置和采用模糊推理方法选择局部调整范围的基础上，应用基于“顺路原则”的局部调整策略实现集送货问题的动态调度计算.40个客户的计算实例表明：动态调度策略能够在保证计算效率的前提下，提高计算精度和结果的可执行性。

1基于局部调整策略的动态调度算法

1.1集送货静态路径方案的构造

市内货物的配送和收集是一个典型的车辆路径问题，具有“带时间窗约束”、“单一车场”、“涉及多种车型”以及“取货和送货一体化完成”等四个典型特征。

考虑到集送货问题的复杂性、典型性和特殊性，以运输车辆的燃油成本Cg、折旧成本Ct、车厢整理成本Cs以及司机工资成本Cd之和为目标函数，建立该调度问题的成本模型：

(1)

C(k)=Cg(k)+Cd(k)+Ct(k)+Cs(k)

(2)

(3)

Di(k)=d(nk,i-1,nki)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：变量i，j和k的取值范围分别为i=1,2,…,N，j=1,2,…,N，k=1,2,…,M，N为当前所需服务的客户总数，M为配送中心当天最多可用的车辆总数，假设各待服务客户的序号为i，其中i=0表示第i个待服务客户为配送中心；h(i)表示第i个客户的收货重量；g(i)表示第i个客户的发货重量；nkj为车辆k的行驶路径上客户j的实际编号；Nk为车辆k的行驶路径包含的路段总数。

式(3~7)为运输车辆燃油成本：β0为车辆空载运输时的油耗与满载运输时的油耗比值；rg为燃油成本比例系数，即运输车辆满载行驶时单位公里的油耗成本，元/km；d(i,j)为运输车辆从第i个客户到第j个客户的实际行驶距离，km；Hi(k)为运输车辆k从第i个客户开往第j个客户时车上总的送货重量，kg；Gi(k)为车辆k从第i个客户直接开往第j个客户时车上总的取货重量，kg；W(k)为运输车辆k的最大核定载重，kg。

式(8)为司机工资成本：r0表示司机单趟发车固定成本，元；rd表示司机行驶里程成本系数，元/km。

式(9)为运输车辆折旧成本(其值与运输车辆的行驶里程成正比)：rt为车辆折旧成本系数，元/km。

式(10)为重新整理车厢的成本：rs为被装卸货物的重量成本系数，元/kg，zij为客户j处是否需要整理客户i处收取的货物。

考虑到静态路径方案是动态调度优化的基础，它的优劣程度直接影响动态优化的结果.因此，采用“混合禁忌搜索算法”(图1)，针对这一车辆路径问题进行初始方案的预求解，其思路主要是先采用经过改进的Clarke-Wright节约算法[9]计算得到一个可行的初始调度方案.在此基础上，再采用改进的禁忌搜索算法[10]对之前得到的初始调度方案进行优化改进，最终实现整个集送货调度问题的求解.应用节约算法构造初始的可行方案的主要优势在于“成本节约值较大的两点将被优先选择”，从而使得产生的初始方案更加科学合理，这使得整个问题的求解速度显著提升.而应用改进的禁忌搜索算法对初始方案进行调整的优势在于能够较容易的跳出局部最优点，从而实现全局范围内的优化搜索。

图1　混合禁忌搜索算法框架Fig.1　Hybrid tabu search algorithm framework

1.2车辆位置的预估修正

动态调度是根据新出现客户的信息和客户出现时运输车辆的当前位置进行调度计算[11].车辆的位置由车上安装的GPS定位终端设备通过GPRS或者3G无线通信网络发送至调度中心.然而实际工作中通常会遇到这样的情况，当司机开始执行新的调度方案时，已经比开始调度计算的时刻T晚了一定的时间间隔ΔT，其数值主要包括动态调度计算时间、无线传输及司机确认时间等.在这一时间间隔ΔT之内，正在执行运输任务的所有车辆，都有可能已经沿着原来的调度方案设定的行驶路线继续行驶了一段距离，极端情况是甚至有可能运输车辆已经到达某一个等待服务的客户处并开始配送服务，从而造成新制定的动态调度计划在执行过程出现偏差.因此，在调度计算过程中需要对车辆位置进行提前预估。

以图2(a)为例对车辆位置的预估方法进行描述.图中虚线条为包含客户A和B的车辆行驶线路，粗实线为车辆在时间间隔ΔT之内的行驶轨迹.车辆位置预估方法描述如下：由车辆行驶车速和车辆预计行驶线路可分别求出车辆到达路口1，2，…，n的时间，因此可判断车辆经过时间间隔ΔT之后的位置。

具体分两种情况：1) 车辆位于路段上：预估的运输车辆的位置恰好在两个路口之间.通常路段本身的长度较小，且路段上运输车辆的行驶方向是单一的，对后续的动态调度优化计算的影响可以忽略，因此，将路段中点作为车辆的预估位置P′.2) 车辆在客户处，如图2(b)所示.具体抽象方法如下：将客户B抽象成一条路段，路段的通行时间为客户B的装/卸货时间，路段两端的路口的经纬度值均为客户B的经纬度值。

图2　车辆位置的预估Fig.2　Vehicle location pre-estimation

另外，考虑到时间间隔ΔT永远小于客户装/卸货时间，车辆在ΔT之内穿越某一客户的情况不会出现，因此，预估车辆位置时不考虑此种特殊情况。

1.3基于模糊推理的局部调整范围选择方法

局部调整算法是在设定搜索范围的条件下，调整现有车辆调度计划，使该调度计划能够及时而准确的满足新增加的所有客户的动态服务需求.因此，选择合适的调整范围(这里主要指参与调整优化计算的线路集合)对于提升算法的精度和计算效率非常重要。

对调整范围的选择有较为重要影响的因素主要有两个：即当前线路与新增加的客户之间距离的远近程度(定义新增加客户至当前线路的距离为新客户到线路上所有客户直线距离的最小值)以及线路上车辆的平均空余体积大小，而平均空余体积的定义为

(11)

式中：Vd为线路上的送货总体积；Vp为线路上的取货总体积.显然，“距离的远近”及“平均空余体积的大小”这两个概念是模糊的，因此笔者采用模糊推理方法来进一步确定合理的调整范围，即判断当前各条运输线路是否应该位于调整范围之内。

将两个主要因素作为因素集合E={新客户与线路之间的距离e1，车厢平均空余体积e2}，而将是否属于调整范围之内作为评价集合F={线路在调整范围之内f1，线路在调整范围之外f2}.因素e1和e2对评价值f1的隶属度函数为

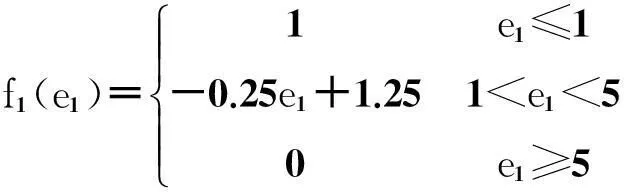
(12)

(13)

由于f1和f2是互为补集的两个结论，因此，只需要列出e1和e2对f1的隶属度函数。

将某一行驶线路和新增加的客户的实际数据分别代入到两个隶属度函数式(12，13)，可计算得到因素e1和因素e2对评价集F的隶属度矩阵R.另外，考虑到因素e1和因素e2对最终评价结果的影响程度也不尽相同，故需要定义两个因素的权重矩阵A.显然在判断给定线路是否位于调整范围之内时，距离因素要比空余体积因素重要，因此选定权值矩阵A=(0.7,0.3).最后，可给出模糊推理的结果为

(14)

式中参数rij为隶属度矩阵R的元素。

根据式(14)可求得模糊推理的计算结果b1和b2.当b1>b2时，推理的结果为线路在调整范围之内.反之，则线路在调整范围之外。

1.4基于“顺路原则”的局部调整策略

一般情况下，局部调整策略往往采用“最接近的原则”作为判断依据来选择合适的调整对象，即选择某一个给定范围之内离新增加的客户“最近”的运输车辆或者客户作为局部调整对象.图3(a)为“接近原则”的示意图，图3中虚线圆圈标识的新增加的客户“9”与客户“1”(在运输车辆“2”的行驶线路中)的距离是相对而言最短的，因此，可以选择客户“1”作为此次局部调整的对象，并将新增加的客户“9”直接插入到当前客户“1”的前面，构造出一个新的调度优化方案.但是，由于动态集送货调度问题的特殊性，距离的远近通常无法有效反应新增运输成本的大小。

与“最接近的原则”不同，“顺路原则”选择调整对象的依据是“是否顺路”，即当前运输车辆服务新增加的客户是否“顺路”.对于“顺路”的含义可以理解如下：在满足时间窗、载重、体积等约束条件的前提之下，将新增加的所有客户依次插入至当前运输车辆的行驶线路中，额外增加的运输成本ΔC越小就表示运输车辆服务新增客户越是“顺路”.ΔC的求解方法为

ΔC(x,y,z)=Cx,z+Cz,y-Cx,y

(15)

式中：ΔC(x,y,z)为将客户z插入x和y之间时新增加的额外成本.图3(b)为基于“顺路原则”局部调整的示例，当新增加的客户“9”被插入至运输车辆“1”的行驶路线上的客户“4”和客户“2”之间的时候，额外增加的运输成本ΔC(4,2,9)最小.因此，将安排运输车辆“1”在完成客户“4”的送货任务之后“顺路”行驶至新增加的客户“9”处收取货物。

图3　局部调整策略示意图Fig.3　Local adjustment strategy diagram

2应用验证

以某大型物流企业实际的集送货动态调度问题为例，验证基于顺路原则及位置预估的集送货动态调度策略的有效性.动态调度开始时，共有40个不同的客户(其中只有4个客户是新增客户).客户位置、车辆位置以及现有路径如图4所示，图4中圆圈内的客户即为新增客户，另外由于显示的原因，图4中只加粗显示其中的两条路径。

通过应用基于模糊推理方法的调整范围选择策略，可以确定4个新增加客户各自的局部调整范围.以图4中方框内的客户为例，采用模糊推理方法，确定其调整范围仅限于图中被加粗显示的两条路径。

图4　客户位置、车辆位置以及现有路径Fig.4　Customers location,vehicle location and directions

图5为该动态调度问题采用基于顺路原则及位置预估的集送货动态调度策略之后的优化结果，包括：7条行驶线路(行驶线路数目并未发生改变)，总的行驶里程为495km，总成本为996 元。

图5　动态调整策略优化结果Fig.5　Results of dynamic dispatch strategy

表1为两类算法的对比情况，表1中基于“接近原则”的局部调整算法的调整范围是所有路径.通过对比分析可知：笔者提出的基于“顺路原则”的局部调算法无论在精度还是效率方面均具有明显优势。

表1　两类算法对比分析

表2为车辆位置预估对调度结果的影响.通过对实际的集送货调度数据分析，选定延迟时间ΔT=180 s，车辆当前车速是v=10 m/s.表2中位置误差是指与GPS数据(即经过ΔT之后车辆的真实位置)的误差，而表2中的成本是指将车辆的真实位置代入两类优化结果之后计算得到的成本，因此，大于表1中的成本996 元.表2充分说明车辆当前位置对优化结果具有重要影响，位置预估越准确则优化结果越精确。

表2　车辆位置预估对优化结果的影响

3结论

在顺路原则及位置预估的集送货动态调度策略的基础上，得出基于模糊推理的局部调整范围之选择方法和基于“顺路原则”的局部调整策略能够在保证精度的前提下，有效提高动态调度优化的效率；考虑优化过程中对车辆位置的变化及车辆位置预估方法的采用，将提高动态调度优化的精度以及优化结果的可执行性。

参考文献：

[1]李军，郭耀煌.物流配送车辆优化调度理论与方法[M].北京：中国物资出版社，2001：99-112。

[2]王飞.带时间窗车辆调度问题的改进粒子群算法[J].计算机工程与应用，2014，50(6)：226-229。

[3]ZHENG Sifa, CAO Jiandong, LIAN Xiaomin. Urban pickup and delivery problem considering time-dependent fuzzy velocity[J]. Computers & Industrial Engineering，2011，60(4)：821-829。

[4]曹剑东，郑四发，李兵，等.考虑分时模糊车速的带时间窗的市内集送货问题[J].系统仿真学报，2009，21(3)：823-826。

[5]胡志华，陶莎.基于混合进化算法的甩挂配送问题[J].公路交通科技，2013，30(5)：147-152。

[6]陈嶷瑛，李文斌，王舵，等.使用面向离散搜索空间的蛙跳算法求解TSP[J].计算机工程与应用,2009,45(27):50-52。

[7]MADSEN O B G, RAVN H F, VOELDS J. A heuristic method for dispatching repairmen[J]. Annals of Operations Reasearch,1995,61:193-208。

[8]GENDREAU M, GUERTIN F, POTVIN J Y, et al. Parallel tabu search for real-time vehicle routing and dispatching[J]. Transportation Science,1996(33):381-390。

[9]CLARKE G, WRIGHT J W. Scheduling of vehicles from a central depot to a number of delivery points [J]. Operations Research,1964,12(4):568-581。

[10]OSMAN I H, WASSAN N A. A Reactive Tabu search meta heuristic for the vehicle routing problem with backhauls[J]. Journal of Scheduling,2002，5(4)：263-285。

[11]李兵，郑四发，曹剑东，等.求解客户需求动态变化的车辆路径规划方法[J].交通运输工程学报,2007,7(1):106-109。

(责任编辑：陈石平)

中图分类号：U492

文献标志码：A

文章编号：1006-4303(2015)02-0197-05

作者简介：曹剑东(1980—)，男，江苏苏州人，副研究员，工学博士，研究方向为智能交通，E-mail:caojiandong@catsic.com。

基金项目：国家自然科学基金资助项目(51405438)

收稿日期：2014-11-25