高频谐振载荷作用下疲劳裂纹尖端变形场分析

高红俐，郑欢斌，刘　欢，刘　辉

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州 310014)

高频谐振载荷作用下疲劳裂纹尖端变形场分析

高红俐，郑欢斌，刘欢，刘辉

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，浙江 杭州 310014)

摘要：为研究高频谐振式疲劳裂纹扩展试验中，带有I型预制裂纹的CT紧凑拉伸试件裂纹尖端位移、应变场的变化规律，利用动态有限元方法，采用ANSYS和MATLAB软件编写程序，计算了CT试件在高频恒幅正弦交变载荷作用下，在一个应力循环及裂纹扩展到不同长度时裂纹尖端区域的位移、应变场并分析了其变化规律.为验证有限元计算结果的准确性，进行了高频谐振式疲劳裂纹扩展试验，采用动态高精度应变仪测量了CT试件疲劳裂纹扩展到5 mm时在一个应力循环内裂纹尖端点的应变.研究结果表明：在稳态裂纹扩展阶段，高频谐振载荷作用下I型疲劳裂纹尖端区域位移、应变均为和载荷同一形式的交变量；随着裂纹的扩展，I型疲劳裂纹尖端的位移、应变幅不断增大；裂纹尖端测量点应变有限元计算结果和实验结果最大误差为2.93%。

关键词：高频谐振载荷；疲劳裂纹尖端；动态有限元；位移场；应变场

Finite element analysis of displacement and strain fields at crack

tip under high frequency resonant loading

GAO Hongli, ZHENG Huanbin, LIU Huan, LIU Hui

(Key Laboratory of E&M, Ministry of Education&Zhejiang Province, Zhejiang University of

Technology, Hangzhou 310014, China)

Abstract:This work researched the variation law of displacement field and strain field at fatigue crack tip of compact tension specimen with type I pre-notch based on dynamic finite element method (FEM) in the high frequency resonant fatigue crack propagation test. The displacement field and the strain field at CT specimen fatigue crack tip in one stress cycle and at different crack lengths under constant amplitude high frequency sinusoidal alternating loading condition are calculated and the related variation laws of the displacement field and the strain field are analyzed. In order to validate the FEM result, the high frequency resonant fatigue crack propagation test was performed, and the dynamic strain gauge is used to measure the strain at crack tip of CT specimen with crack length of 5mm during one stress cycle. The research results show that during crack stable propagation stage, the displacement and the strain at type I fatigue crack tip are the same form with the high frequency resonant load; the displacement and strain increase with the crack growth. The maximum error of the strain at crack tip between the calculated result by FEM simulation and the experimental result is 2.93%。

Keywords:high frequency resonant load; fatigue crack tip; dynamic FEM; displacement field; strain field

疲劳破坏是机械零部件失效的主要形式，材料或构件在交变载荷的作用下，疲劳裂纹的产生和扩展是造成疲劳破坏的主要原因.由于目前尚不能完全通过有效的理论方法来研究，采用特定的材料疲劳裂纹扩展试验，来探索零部件扩展断裂过程的规律，对提高机械产品的可靠性和使用寿命有着十分重要的意义[1-3].实际工程构件中裂纹形式大多属于I型张开裂纹，也是最危险的一种裂纹形式，疲劳裂纹扩展试验采用具有I型预制裂纹的标准CT试件来进行试验，通过测量试件在交变载荷作用下，疲劳裂纹扩展速率da/dN和裂纹尖端应力强度因子幅ΔK之间的关系来研究材料的疲劳裂纹扩展规律，另外，裂纹的萌生、扩展和断裂不能完全由宏观裂纹形态和尺寸a来表征，要系统全面研究疲劳裂纹扩展机理，除了研究宏观裂纹的扩展规律da/dN和ΔK的关系，研究疲劳裂纹扩展过程中裂纹尖端位移、应变、应力场等力学特征参数的变化规律是非常必要的。

疲劳裂纹扩展试验[4-5]包括基于电液式强迫振动系统的低频疲劳试验和基于电磁谐振式振动系统的高频疲劳试验，前者，试验振动频率一般为1～10 Hz，后者则是基于共振原理的用于测定金属材料及其构件在高频谐振载荷作用下疲劳特性的测试装置，试验振动频率一般为80～300 Hz左右，由于其工作频率高、能量消耗低、试验时间短以及试验波形好等优点被力学实验室广泛用来进行材料疲劳试验.电液式强迫振动疲劳裂纹扩展试验裂纹尖端位移、应变和应力场的计算可以采用静力学的方法进行计算，但在采用标准CT试件进行的高频谐振式疲劳裂纹扩展试验中，试件在高频谐振载荷作用下高速振动，由于要考虑惯性效应和应力波传播效应[6-7]，使得裂纹尖端位移、应变的计算问题变得更加复杂，其解析解至今还未得到.多年来，已有众多学者对裂纹尖端位移、应变场进行了实验和理论研究[8-10]，但基本是在静态和准静态的情况下，笔者针对高频谐振式疲劳裂纹扩展试验中的标准试件CT试件进行了动态有限元计算，研究了在恒幅高频正弦交变载荷的作用下疲劳裂纹扩展过程中I型裂纹尖端位移、应变场的变化规律，为进一步研究高频谐振载荷作用下疲劳裂纹扩展机理和扩展参数的测量奠定了理论基础。

1高频谐振式疲劳裂纹扩展试验

电磁谐振式高频疲劳试验机是基于共振原理的用于测定金属材料及其构件在高频谐振载荷作用下疲劳特性的测试装置，目前国内主流机型结构PLG-100,如图1所示，其为一双自由度的谐振式振动系统[2]，当电磁激振器的激振频率与试验机振动系统本身的固有频率基本一致时，试验机振动系统便发生共振，在共振状态下工作台的振动振幅将增加数倍，这样作用在CT试件上的正弦交变载荷的幅值也随之增加，使试验在功率消耗很小的情况下进行.图2为疲劳裂纹扩展试验标准CT试件尺寸图，图3为疲劳裂纹扩展试验CT试件和夹具安装图，图4为谐振式疲劳裂纹扩展试验正弦交变载荷，其中Fmax为最大载荷，Fmin为最小载荷，Fm为平均载荷，Fa为振幅，谐振式疲劳裂纹扩展试验在一个应力循环内，CT试件均处于拉应力状态，这样在图3的安装方式下，可认为CT试件的上加载孔的上半圆柱面和试件的下加载孔的下半圆柱面与定位销轴面接触，传递载荷到试件上。

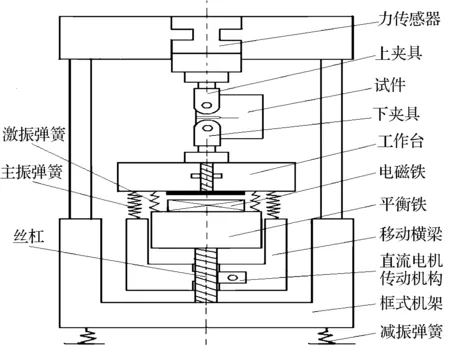
图1　电磁谐振式疲劳试验机主机结构图Fig.1　The structure of resonant fatigue tester

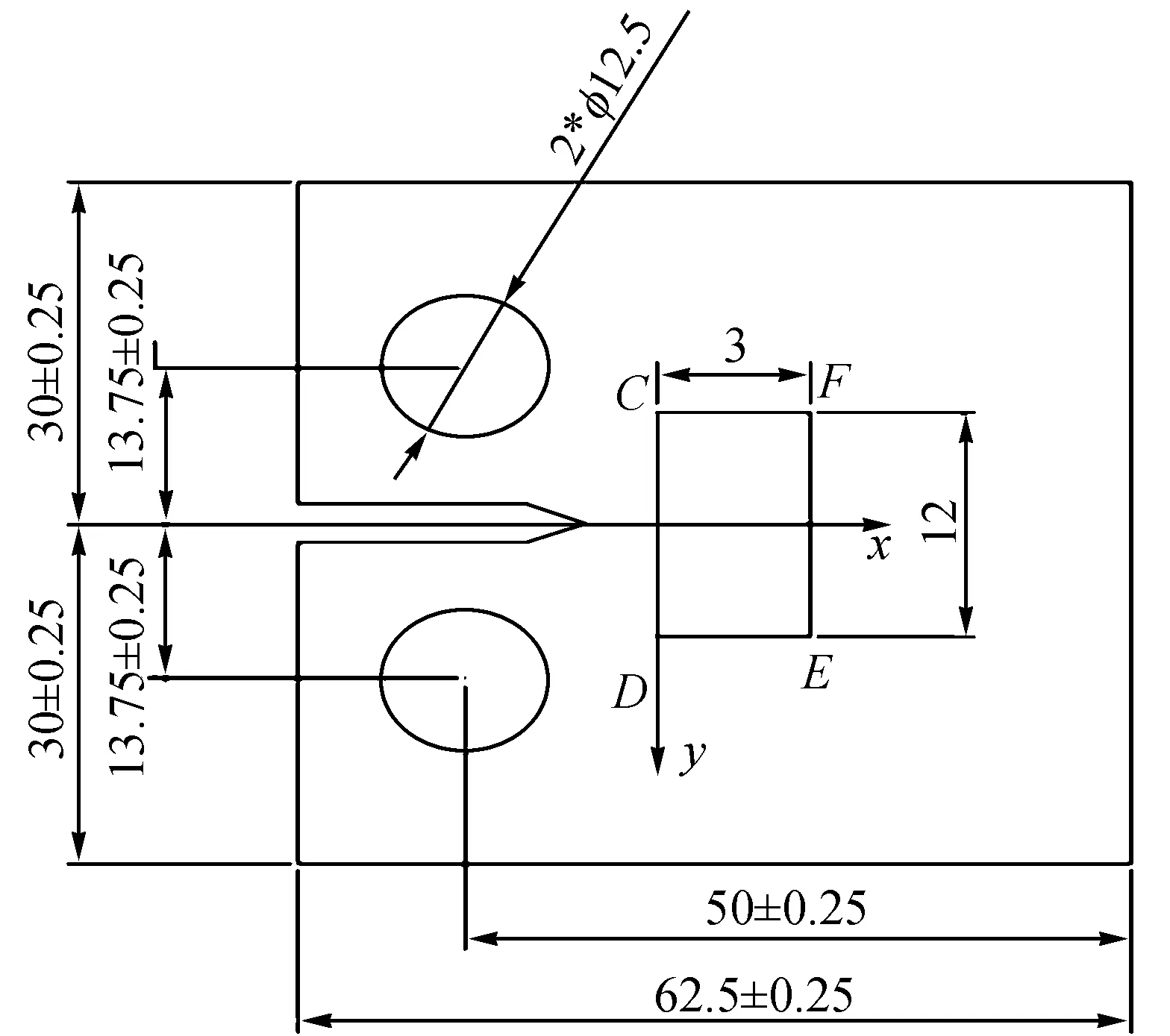
图2　标准CT试件尺寸图Fig.2　The dimensioned drawing of CT specimen

采用图1所示试验装置进行了多种材料的标准CT试件谐振式疲劳裂纹扩展试验，试验结果表明：在稳态裂纹扩展阶段，系统的谐振频率范围在90～135 Hz，这样为简化计算过程，在研究高频谐振载荷作用下疲劳裂纹尖端位移、应变的变化规律时采用125 Hz的正弦交变载荷进行计算。

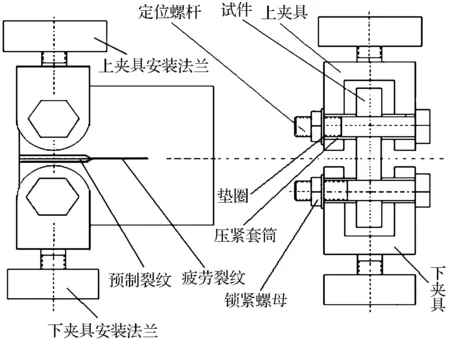
图3　疲劳裂纹扩展试验CT试件和夹具安装图Fig.3　The installation drawing of CT specimen

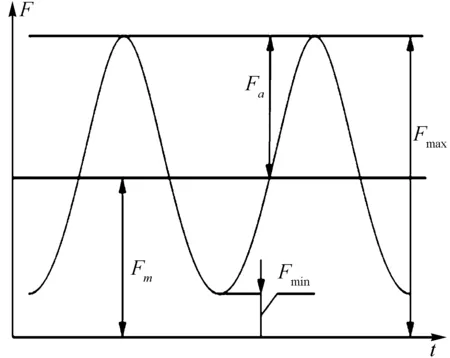
图4　谐振式疲劳裂纹扩展试验交变载荷Fig.4　Sinusoidal alternating load

2高频谐振载荷作用下CT试件有限元建模

2.1疲劳裂纹尖端动态位移、应变场计算方法

对CT试件在高频谐振载荷作用下裂纹尖端的位移、应变场进行计算，试件上所施加的交变载荷如图4所示，它是静载荷和正弦交变载荷共同作用的结果.当CT试件只受静载荷作用时，可以采用ANSYS中的静力学分析计算其位移及应变；当CT试件只受正弦载荷作用时，可以对其进行谐响应分析.但是当静载荷和正弦载荷两者共同作用在CT试件上，单独采用静力学分析或单独采用谐响应分析都无法求解[11]。

根据振动理论，求在随时间变化载荷作用下的响应，实际上就是求解系统动力学方程：

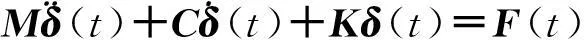
(1)

式中：M为系统的质量矩阵；δ为系统的总体位移列阵；C为系统的阻尼矩阵；K为系统的总体刚度矩阵；F(t)为系统的总体载荷列阵，F(t)=f(t)+f0，其中f(t)为正弦载荷，f0为静载荷.即

(2)

将方程式(2)分解成两个方程

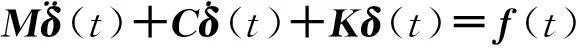
(3)

(4)

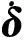
Kδ=f0

(5)

假设δ1为方程式(3)的解，δ2为方程式(5)的解，由于质量矩阵M，阻尼矩阵C及刚度矩阵K均为常量矩阵，显然δ=δ1+δ2为方程式(2)的解.所以可以利用有限元软件ANSYS，对CT试件在正弦载荷作用和静载荷作用下分别进行计算分析，可以得到相应的位移解δ1和δ2.ANSYS中直接给出的是解的实部δ1r，δ2r和虚部δ1i.δ1由实部δ1r和虚部δ1i组成，用极坐标形式表示复数δ1，可得δ1=δ1rcoswt+δ1isinwt，δ2仅由实部δ2r组成.将δ1和δ2进行迭加得到δ，并用时间函数形式表示为

δ=δ1+δ2=δ1rcoswt+δ1isinwt+δ2r

(6)

式中：w为正弦载荷f(t)的频率.按方程式(6)就可以得出CT试件各节点任意时刻的位移，即动态位移.则该时刻相应的应变，表示为

ε=Bδe

(7)

式中:ε为单元内任意一点的应变；B为单元几何矩阵；δe为单元节点位移列阵。

2.2裂纹尖端奇异性处理

由断裂力学的理论知道，在裂纹尖端附近具有应力奇异性，即在裂纹尖端附近各应力分量都与r-1/2成正比关系，当r→0时，应力会急剧增加.在常规的有限元法中，一般均采用多项式来表示单元内部应力和位移，但在奇异点附近却不能很好地反映出应力的变化.为了解决这个困难，一般采取以下两种办法：一种是将裂纹尖端附近的网格划分得非常细，但采取这种办法，节点会很多，计算量也会相应增大；另一种是在裂纹尖端处设置一种特殊的奇异单元，用以更好地反映出应力场的奇异性，在这些特殊奇异单元的外面，仍采用常规的单元.采用奇异等参数单元(1/4边中点法)，即把8结点等参数单元的边中节点从正常位置移至1/4边长处，在角点附近即出现r-1/2级的应力奇异性如图5所示.在裂纹尖端处，布置如图6所示的4个奇异等参数单元，即能较好地反映裂纹尖端附近的应力场。

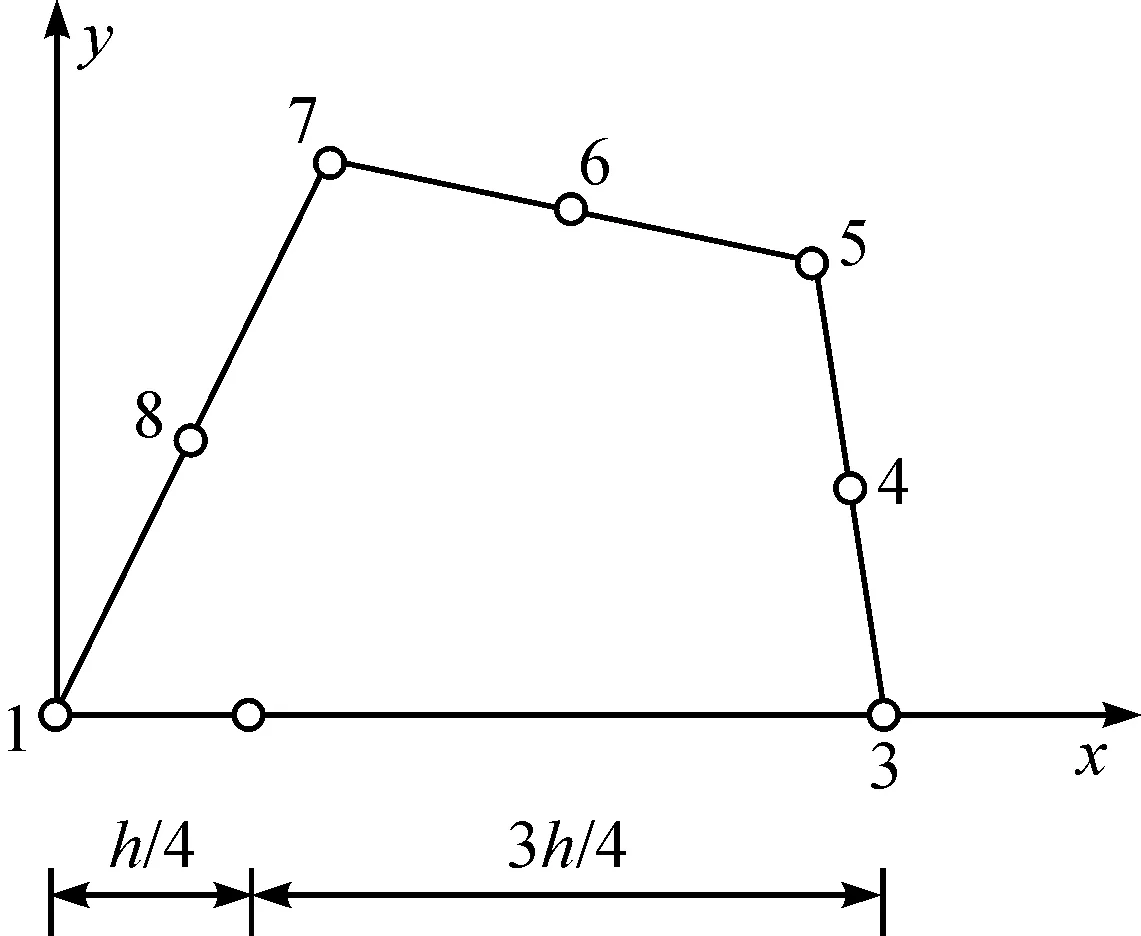
图5　应力奇异性Fig.5　The stress singularity

图6　布置4个奇异等参数单元Fig.6　Four singularity isoparametric elements at crack tip

2.3疲劳裂纹尖端有限元网格划分及约束

图2为含预制裂纹的紧凑拉伸试件，厚度为12.5mm，裂纹长度为5mm，该试件材料为45#钢，弹性模量E为206GPa，泊松比为0.27，密度为7 800kg/m3.采用逐节点直接建模方法：先生成节点，再由节点生成单元和结构.使用ANSYS建立有限元模型时，首先选用平面8结点四边形等参单元PLANE82建立二维模型，划分网格时，在裂纹尖端通过ANSYS命令KSCON将其在裂纹尖端附近退化成6结点三角形等参单元，并将有关边的边中结点向裂纹尖端靠拢，都移置1/4边长处，以圆周的方式布置在裂纹尖端周围.然后再使用SOLID95单元拉伸成体单元，网格划分如图7所示.将CT试件上孔的上半圆柱面设置为固定状态，在试件的下孔的下半圆柱面设置为受力面。

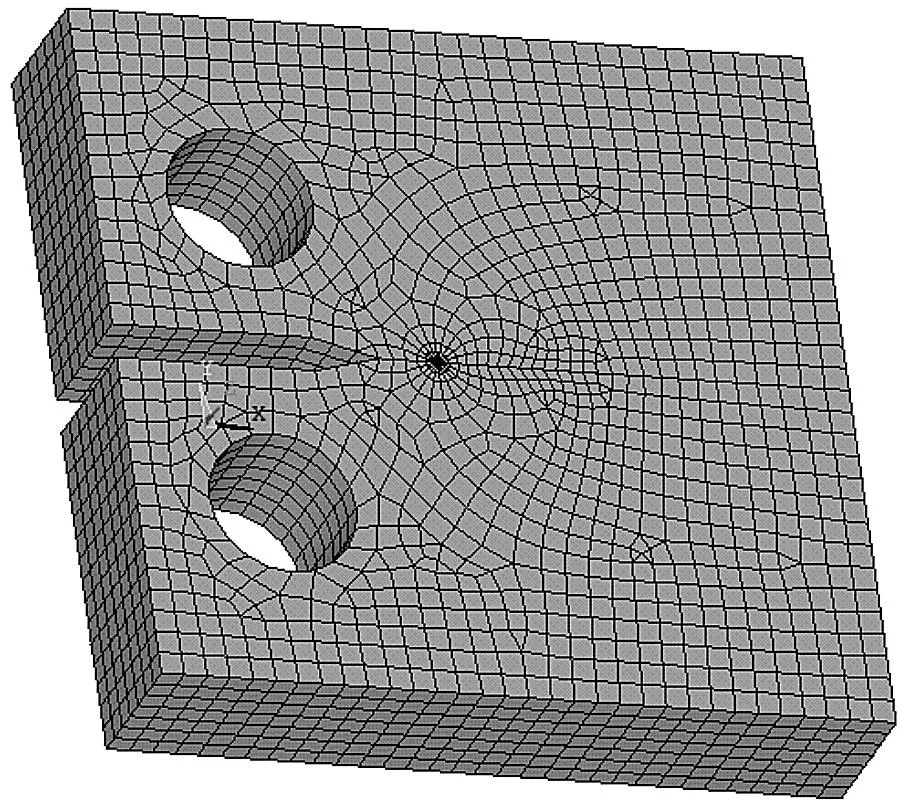
图7　CT试件三维模型网格划分Fig.7　The three-dimensional model mesh

3高频谐振载荷作用下CT试件裂纹尖端变形场

3.1疲劳裂纹无扩展时CT试件变形场的变化规律

3.1.1CT试件裂纹尖端位移场的变化规律

研究具有一定长度疲劳裂纹的CT试件在高频谐振载荷一个应力周期下，在裂纹没有扩展时裂纹尖端区域位移场的变化规律.首先以疲劳裂纹长度为5mm的CT试件为例进行计算，得到裂纹尖端区域位移场的变化规律，然后对不同长度疲劳裂纹的情况也进行了相应计算，对计算结果进行了验证.试件尺寸及裂纹尖端计算区域如图2所示.对其分别进行静力学分析和谐响应分析，所施加的载荷为正弦载荷f(t)=(1.35sin785t)kN，静载荷f0=7kN.位移场的计算方法与有限元建模方法如2.1和2.3所述.为了更为直观地观察裂纹尖端位移场的变化，采用自编的Matlab程序进行有限元计算结果的后处理，得到裂纹尖端矩形区域位移场的三维图及裂纹尖端处位移的二维图。

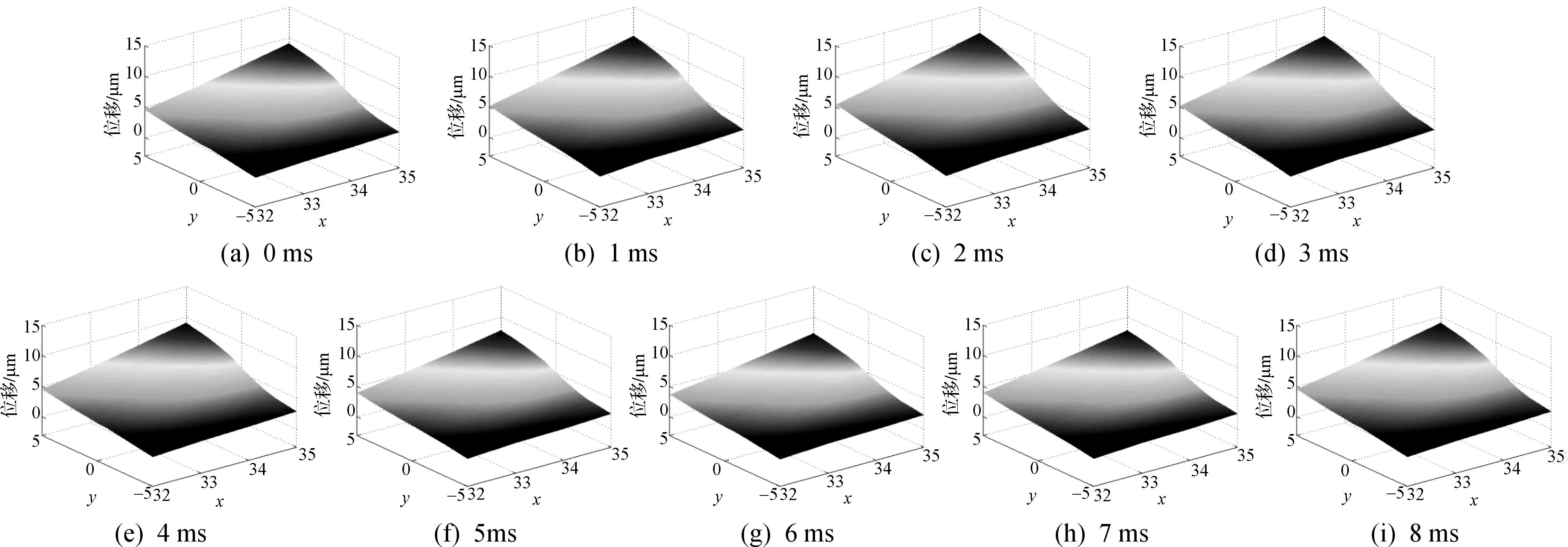
图8　疲劳裂纹无扩展时裂纹尖端位移场Fig.8　The crack tip region displacement fields

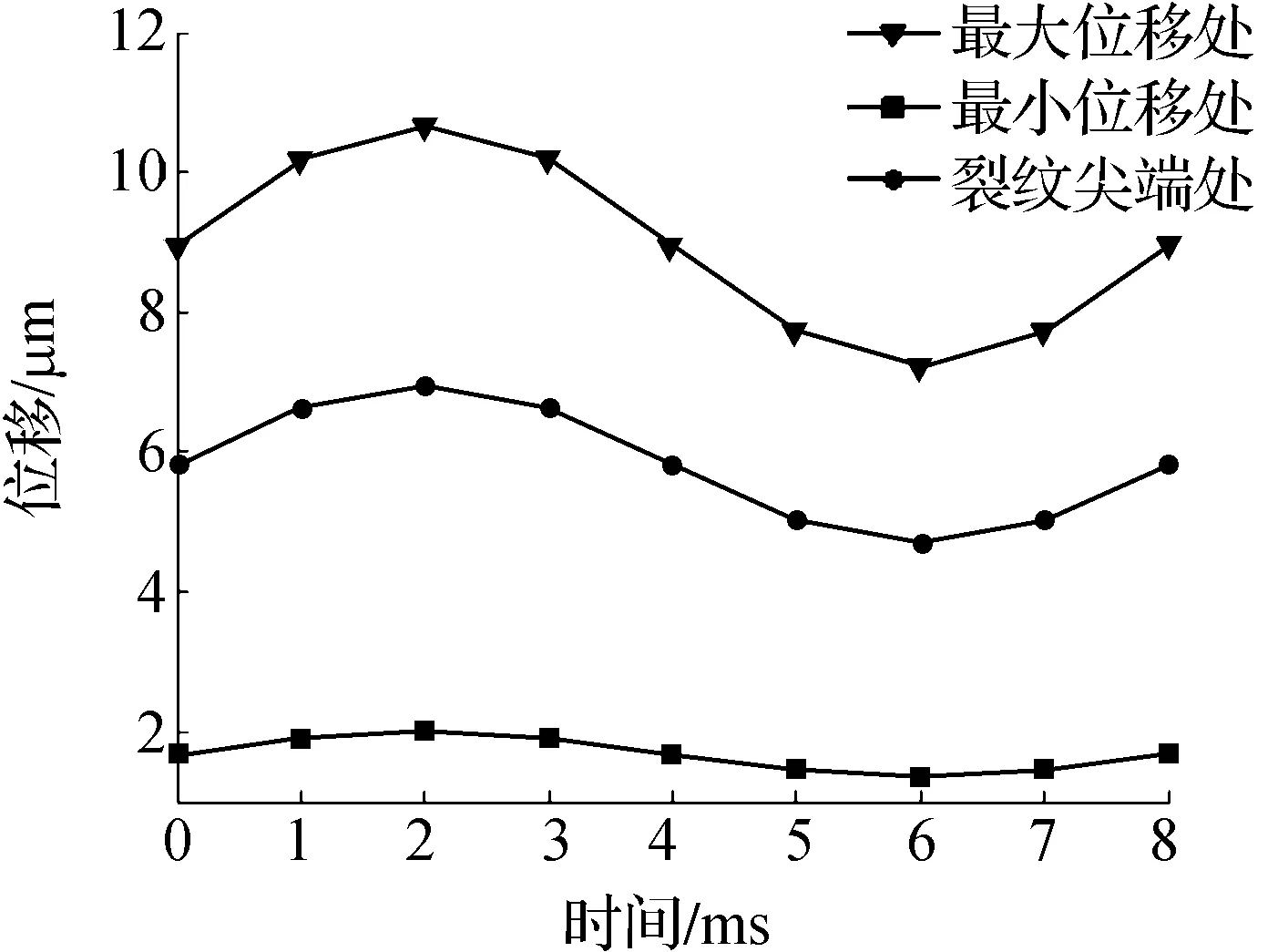
图9　最大处、最小处及裂纹尖端处位移Fig.9　Maximum, minimum and crack tip displacements

图8中九组图直观地表现了在一个应力循环周期8ms内，裂纹尖端区域Y向位移场的变化.位移场中最大位移值都位于如图2所示矩形区域D点附近，最小位移值都位于如图2所示矩形区域F点附近.造成这种现象的原因是因为矩形区域中D点离载荷施加处最近，F点离载荷施加处最远.图9体现的是在一个应力循环周期内，裂纹尖端区域内D处最大位移值，F处最小位移值以及裂纹尖端处位移值随时间的变化.可以看出：裂纹尖端区域内最大位移，最小位移以及裂纹尖端处位移是正弦变化的，与施加的载荷有着相同的变化规律。

3.1.2CT试件裂纹尖端应变场的变化规律

与求解裂纹尖端区域位移场相同的方法，得到在CT试件裂纹尖端区域一个应力周期内，不同时刻的应变场以及裂纹尖端处应变的变化.图10中九组图直观地表现了在一个应力循环周期内，裂纹尖端区域应变场的变化.应变场中的最大应变值都在裂纹尖端处，这是因为裂纹尖端处是应力集中位置.应变场的形状大抵相似，在裂纹尖端矩形区域中沿裂纹扩展方向基本呈对称分布，裂纹尖端处应变值出现明显的突变，应变值达到最大值，沿裂纹扩展方向应变值逐渐减小.图11体现了在一个应力循环内，在裂纹无扩展时，裂纹尖端处应变随时间的变化.可以看出：裂纹尖端处的应变也是正弦变化的，与载荷有着相同的规律变化，计算表明：裂纹尖端区域其他点的应变值具有和裂纹尖端点同样的变化规律。

图10　疲劳裂纹无扩展时裂纹尖端应变场Fig.10　The crack tip region strain fields

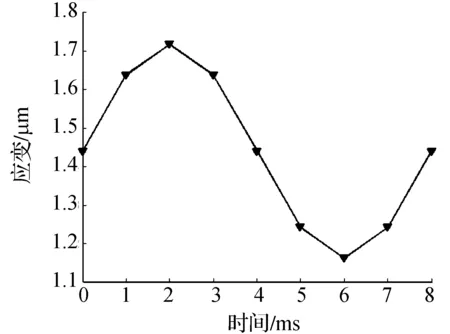
图11　裂纹尖端处应变Fig.11　The crack tip strain in one load cycle

3.2疲劳裂纹扩展时CT试件变形幅场的变化规律

3.2.1CT试件裂纹尖端位移幅场的变化规律

图12　不同裂纹长度时的位移幅场Fig.12　The displacement amplitude field with different crack length

在高频疲劳裂纹扩展试验中，试件施加的载荷是正弦变化的，为了方便研究CT试件在高频谐振载荷作用下疲劳裂纹扩展过程中位移场的变化规律，引入“位移幅场”的概念，将同一应力循环下载荷最大处的位移场与载荷最小处的位移场进行相减得到裂纹尖端位移场幅的分布规律.图12为疲劳裂纹扩展到不同长度时裂纹尖端区域位移幅场，从图12(a)中可以看出：当裂纹长度为5mm时，裂纹尖端的位移幅场比较平缓.而从其余3组图片中可以看出：随着裂纹长度的增加，裂纹尖端的位移幅场越来越陡峭.这说明在疲劳裂纹扩展过程中，随着裂纹长度的增加，裂纹尖端位移场的变化也会越来越大。

3.2.2CT试件裂纹尖端应变场幅的变化规律

同样，为了方便研究CT试件在高频谐振载荷作用下疲劳裂纹扩展过程中应变场的变化规律，引入“应变幅场”的概念，将同一应力循环下载荷最大处的应变场与载荷最小处的应变场进行相减得到裂纹尖端应变幅场的分布规律.图13为疲劳裂纹扩展到不同长度时裂纹尖端区域应变幅场，从图13(a)中可以看出：当裂纹长度为5mm时，裂纹尖端的应变幅场比较平缓.而从其余3组图片中可以看出：随着裂纹长度的增加，裂纹尖端的应变幅场越来越尖锐，尤其是裂纹尖端处的应变.这说明在疲劳裂纹扩展过程中，随着裂纹长度的增加，裂纹尖端应变场的变化也会越来越大。

图13　疲劳裂纹扩展到不同阶段裂纹尖端应变幅场Fig.13　The strain amplitude field with different crack length

4疲劳裂纹尖端处应变值的实验验证

为验证上述疲劳裂纹在无扩展时裂纹尖端处应变的动态有限元计算结果，在带有5mm疲劳裂纹的CT试件表面贴上电阻应变片并进行疲劳裂纹扩展实验，实验是在自行研制的电磁谐振式高频疲劳试验平台上进行的，实验装置实物如图14所示，包括试验载荷加载系统、裂纹尺寸在线测量系统和固有频率跟踪系统和载荷控制系统，试验载荷加载系统由高频疲劳试验机、CT试件、电磁激振器及其放大电路组成，主要完成将电磁激振器所产生的正弦激振力作用在试验台上，使试验台产生相同频率的正弦振动，从而使正弦试验载荷作用于CT试件上的功能.裂纹尺寸在线测量系统：包括光源、CCD图像传感器、光学镜头、图像采集卡及计算机，此系统主要用于在线测量疲劳裂纹扩展过程中的裂纹尺寸.载荷控制系统和固有频率跟踪系统，用于控制试验载荷并跟踪裂纹扩展过程中的固有频率.其中疲劳试验机采用如图1所示的红山PLG-100谐振式高频疲劳试验机，镜头为SONY35mm定焦镜头,图像采集卡为美国NI公司所生产的PCI-1014图像采集卡，CCD为XC-XT50CE黑白CCD摄像头，分辨率为724X568，试件材料为退火处理后的45#钢。

图14　实验平台实物图Fig.14　The image of the experimental facility

首先将带有预制裂纹的CT试件安装在疲劳试验机上，此时系统的谐振频率为126.4Hz,施加试验载荷：Fmax=11.65kN，Fmin=6.35kN，Fm=9kN，频率为126.4Hz，进行疲劳试验，由裂纹尺寸在线测量系统实时测量扩展疲劳裂纹长度，固有频率跟踪系统和载荷控制系统实时跟踪固有频率和控制实验载荷，当裂纹扩展至5mm时停机，取下试件,在试件表面粘帖电阻应变片，由于裂纹尖端存在三维效应及应变梯度，所以电阻应变片不能过于接近裂纹尖端，但为了保证裂纹尖端应变值的测量精度，电阻应变片也不能过于远离裂纹尖端[12].采用的贴片方式如图15所示，根据现有经验，θ=54.27°，r=12.5mm，φ=68.01°.按仪器要求组桥连线，为了测量CT试件裂纹尖端处随时间变化的动态应变，实验采用XL2102A型动态电阻应变仪，其工作频率在DC～100kHz，电磁谐振式高频疲劳试验系统的工作频率为50～300Hz,可见，此仪器完全满足实验条件.将带有5mm疲劳裂纹并贴有电阻应变片的试件安装在谐振式疲劳试验机上，此时系统谐振频率为125Hz，为防止裂纹快速扩展将试验载荷降至Fmax=8.35kN，Fmin=5.65kN，Fm=7kN，系统在此参数下起振进行试验，采用动态电阻应变仪测得一个载荷周期内，裂纹尖端处的应变值，并与有限元法得出的应变值做比较，结果如表1所示。

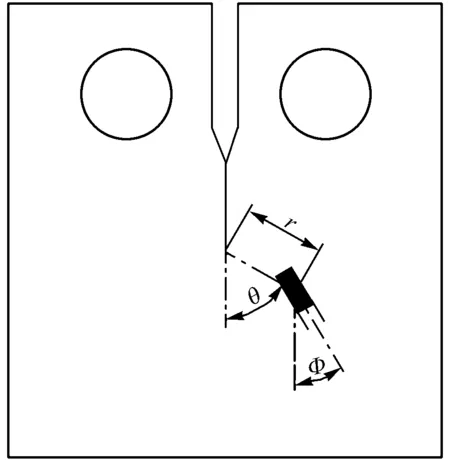
图15　应变片贴片图Fig.15　Arrangement of one strain gauge

时间/ms012345678有限元法/μm1.4401.6431.7121.6431.4401.2461.1671.2461.440应变片法/μm1.4071.5991.6741.6071.4061.2151.1351.2211.399误差/%2.352.752.272.242.412.552.822.052.93

从表1可知：运用动态有限元法在求解CT试件裂纹尖端处应变时，具有较高的精度.与用贴应变的实验方法做比较，最大的误差是2.93%.有限元计算结果高于实际测量结果，这是由于裂纹尖端附近应变梯度非常大，而应变片法测量的是测试范围内的平均应变。

5结论

采用ANSYS静力学分析与谐响应分析结合的方法，研究了CT试件在高频恒幅正弦交变载荷下，在一个应力循环周期内及裂纹扩展到不同长度时裂纹尖端区域的位移及应变场的变化规律；通过在CT试件上贴应变片的实验方法验证了动态有限元法在求解裂纹尖端处应变值的准确性.通过比较分析结果表明：对于同一疲劳裂纹，I型裂纹尖端位移及应变场均为和载荷同一形式的交变量；随着裂纹的扩展，I型裂纹尖端的位移及应变场不断增大；利用动态有限元法计算CT试件裂纹尖端处的应变值，有较高的精度。

参考文献：

[1]熊缨，陈冰冰，郑三龙，等．16MnR钢在不同条件下的疲劳裂纹扩展规律[J]．金属学报，2009，45(7):849-855。

[2]苏彬，邢海军，赵颖娣，等．循环载荷应力比对微动疲劳特性的影响[J]．浙江工业大学学报，2011，39(4):445-451。

[3]邢海军，赵颖娣，俞新宇，等．45号钢微动疲劳门坎值特性研究[J]．浙江工业大学学报，2011，39(6):661-665。

[4]张妮．高频疲劳试验机动态特性的研究[D]．杭州：浙江工业大学，2009。

[5]高红俐，张立彬，姜伟，等．电磁谐振式疲劳裂纹扩展试验固有频率跟踪系统[J]．兵工学报，2013，34(7):896-903。

[6]WALCKER A, WEYGAND D, KRAFT O. Inertial effects on dislocation damping under cyclic loading with ultra-high frequencies[J]．Materials Science and Engineering，2010，31(8):4023-4028。

[7]AMIRKHIZI A V, TEHRANIAN A, NASSER S N. Stress-wave energy management through material anisotropy[J]．Wave Motion，2010，47(8):519-536。

[8]许杨中，金杰．数值模拟在棒材热轧过程及缺陷预测中的应用[J]．浙江工业大学学报，2011，39(3):308-311。

[9]SAKAUE K, UCHIYAMA Y, TANAKA H, et al. Evaluation of crack tip stress and strain fields under nonproportional loading in a viscoelastic material[J].Engineering Fracture Mechanics，2008，75(14):4140-4150。

[10]杨楠，佟景伟，舒庆琏，等．裂纹纹尖弹塑性应力应变场的实验研究和数值分析[J]．实验力学，2003，18(3):338-341。

[11]JIANG F C, ASHISH R, KENNETH S V, et al. Crack length calculation for bend specimens under static and dynamic loading[J]．Engineering Fracture Mechanics，2004，71(13/14):1971-1985。

[12]CHAKRABORTY D, MURTHY K S R K, CHAKRABORTY D. A new single strain gage technique for the accurate determination of mode I stress intensity factor in orthotropic composite materials[J]．Engineering Fracture Mechanics，2014，124:142-154。

(责任编辑：陈石平)

中图分类号：TP394.1；TH691.9

文献标志码：A

文章编号：1006-4303(2015)02-0190-07

作者简介：高红俐(1968—)，女，河北承德人，副教授，博士研究生，主要从事系统动态特性分析与控制方面的研究，E-mail：ghlzjut@126.com。

收稿日期：2014-12-10