西南红层泥岩压实粉碎粘土的真三轴试验研究
刘俊新,刘育田
(西南科技大学 土木工程与建筑学院,四川 绵阳 621010)
西南红层泥岩压实粉碎粘土的真三轴试验研究
刘俊新,刘育田
(西南科技大学 土木工程与建筑学院,四川 绵阳 621010)
摘要:岩土材料与金属材料不同,其强度和变形与其所处的应力状态相关.利用西安理工大学研制的土工真三轴试验装置对西南红层泥岩压实粉碎土在不同中主应力系数和最小主应力条件下进行了真三轴试验研究,分析了其应力-应变曲线的变化规律、中主应力系数b对其峰值应力和峰值应变、抗剪强度参数的影响以及试件破坏方式,并在此基础上引入形状函数,对不同形状函数在π平面上的图形进行对比,发现数据点与莫尔-库伦准则和Rubin提出的函数逼近程度最好,但Rubin函数能够克服莫尔-库伦函数存在的一阶不连续点而造成的数值计算不收敛等困难并且其灵活性更大,适用面更广.因此,这些成果对于研究土石坝和高填方路基工程的变形和破坏的发展规律具有一定的参考价值.
关键词:压实粉碎粘土;中主应力系数;破坏方式;真三轴试验;形状函数
Experimental research on crushed compacted clay from southwest red
layers mudstone with true tri-axial apparatus
LIU Junxin, LIU Yutian
(School of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, China)
Abstract:Compared with metal materials, Geotechnical materials have different characteristics, whose strength and deformation are associated with the three-dimensional stress state. Based on the true tri-axial apparatus of Xi’an University of Technology, the influence of intermediate principal stress on stress-strain curve , stress and strain at the peak, shear strength parameters of crushed compacted clay from southwest red layers mudstone and the failure modes of samples were analyzed under the condition of different intermediate principal stress ratio b and minimum principal stress. Based on the results, compared with the curves from different shape functions on the deviatoric stress plane, it is shown the data points are approximate to the yield locus of Mohr - Coulomb criterion and Rubin’s function. But Rubin’s function can overcome the shortage of Mohr - Coulomb criterion that the order discontinuity points could easily lead to numerical difficulties such as non-convergence and what’s more, its use is of greater flexibility and broader applicability. Therefore, these results have certain reference value for the achievements of the development law of deformation and failure of earth-rock dam and high embankment engineering.
Keywords:crushed compacted clay; intermediate principal stress ratio; failure modes; true tri-axial tests; shape function
红层泥岩作为软弱土层,具有易风化、遇水易软化、崩解等特点,红层泥岩作为填料用于公路和铁路路基以及土石坝上时,必须经过粉碎处理[1-2].在我国的西南地区由于填料的缺失,红层泥岩经粉碎处理后广泛用作土石坝、高速公路和铁路的路基填料.在建设和运营阶段,作为路基和土石坝的土体处于三向主应力不等的状态下,而土体的强度和变形与土体所处的应力状态是相关.常规三轴试验装置由于仅对土样施加2个方向的大小不等主应力,使其处于轴对称的应力状态,因此只能反映轴对称应力状态下土体的强度和变形规律,而忽略了中主应力对其力学特性的影响,不能表征土体在实际应力状态下的力学性能[3-4].为此,人们为了克服常规三轴试验装置带来的不足,而研发出了能反映土体真实应力状态下的三轴试验装置[5-7],即真三轴仪.由于真三轴试验装置能独立地对土样施加3个大小不等的主应力,可以分析不同主应力对土体强度和变形特性的影响,因此更能真实地模拟土体所处的真实应力状态,有利于研究真实应力状态下土体的强度和变形发展规律以及建立反映真实应力状态的本构模型.目前,国内针对真三轴试验研究主要集中在砂土[8-10]、黄土[11-13].
综上所述,土体的强度和变形特性与土体所处的真实应力状态是相关,因此,为了研究压实粉碎的红层泥岩填料在真实应力状态下的强度和变形发展规律以及在π平面上屈服轨迹,笔者以西南红层泥岩粉碎土为土材,利用西安理工大学邵生俊教授自主研制的土工真三轴仪,对西南红层粘性土进行了试验研究.
1试验装置与试验方法
1.1试验装置及试样
本次试验采用西安理工大学自主研发的两向柔性一向刚性新型真三轴仪[14],该仪器克服了三向刚性加载时的相互干扰,也克服了三向柔性加压时两柔性面相交处受力复杂的缺点.试样以西南红层泥岩粉碎土为土材,其尺寸为70 mm×70 mm×70 mm,制样的压实度为95%和含水量为13%(最大干密度γd,max=2.02 g/cm3,最佳含水量ωopt=12.87%),试样采用分层静压而成.
1.2应力路径
b是反映三个主应力相对大小的参数,称为中主应力系数,其表达式为
(1)
由于在试验过程中通常保持最小主应力σ3不变,同步地增加σ1和σ2,而b值保持不变,对式(1)进行求导,可得
dσ2=bdσ1
(2)
在本次试验过程中,为了保持试验开始时的三个方向的主应力相等,首先在三个方向上施加的相同的压力,然后保持第三主应力σ3不变,对第一主应力和第二主应力按式(2)进行等比例加载,这样b值在加载的任意时刻都保持相等.
1.3试验方案
为了获取不同最小主应力、不同b值组合情况下,西南红层压实粘性土的应力-应变关系曲线,进行了不同最小主应力和中主应力系数b值的真三轴试验.试验加载方式为变形加载,其位移速率为0.03mm/s,试验参数的具体组合见表1.
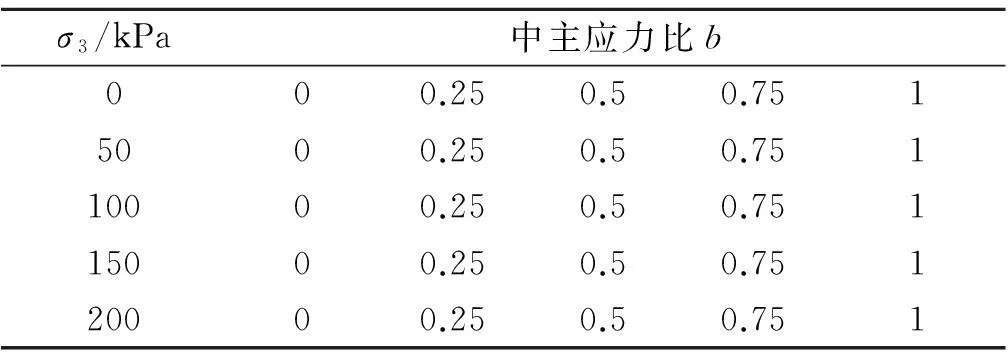
表1 试验控制条件
2试验结果及分析
图1为西南红层压实粘性土真三轴试验的轴向应力-轴向应变曲线,从图中可以知道,在真三轴应力状态下,峰值偏应力随最小主应力的增大而增大,但与中主应力系数b的关系却比较复杂.当最小主应力为“0”时,峰值偏应力随b值的增加表现出先增加而后减少的趋势,并在b=0.5时达到最大值,最小主应力为其它值时,峰值偏应力随b值的变化规律基本相同,只是在b=0.75时达到最大值,同时峰值前曲线的变化率与峰值偏应力随b值的变化规律基本相同,而峰值应变随b值的变化规律恰好与峰值前曲线的变化率和峰值偏应力相反,其随b值的增加表现出先减小而后增大的趋势,只是在b=0.5或0.75达到最大,具体见图2.

图1 不同最小主应力和b值下的应力—应变关系Fig.1 Curves of axial Deviatoric stress versus strain under different minimum principal stress and intermediate principal stress ration b
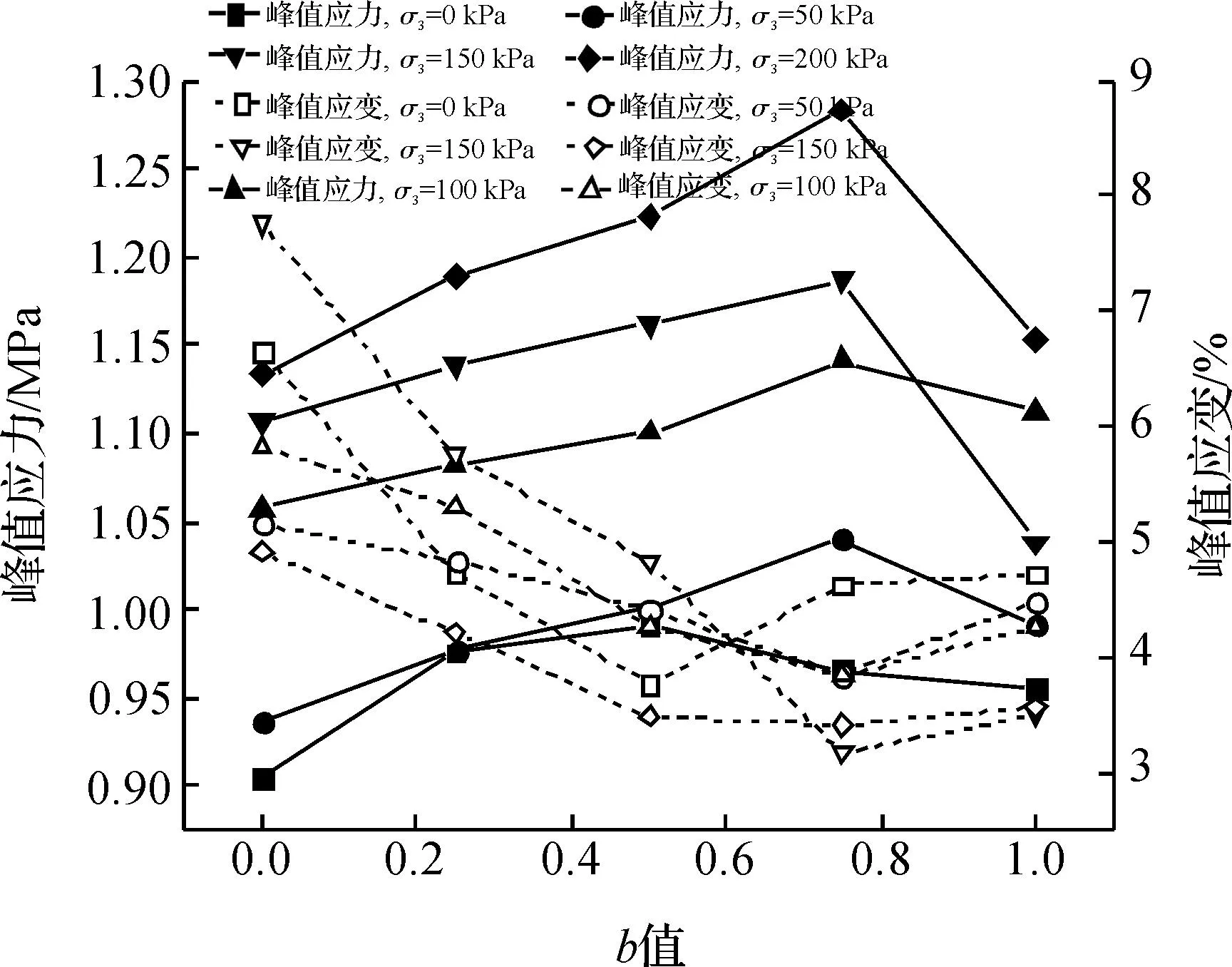
图2 不同最小主应力下峰值应力和应变与b值的关系Fig.2 Curves of axial stress and strain at the peak wih intermediate principal stress ration b under different confining pressures
为了分析b值对土体抗剪强度参数的影响,将试验数据整理成为最小主应力与最大主应力绘出的应力莫尔圆,得出不同b值下的粘聚力c13和内摩擦角φ13,分析中主应力系数对抗剪强度的影响规律.从图3可知:粘聚力c13先随b值的增加而增加,但当b≥0.25后基本上保持不变,内摩擦角φ13随b值的增加先增加而后减小,在b=0.75时达到最大,其抗剪强度参数的变化发展规律与文[11]中Q2黄土不同.图4为不同b值的抗剪强度指标c13和φ13与b=0的抗剪强度指标c13和φ13的比值且用η和α表示粘聚力比和内摩擦角比,从图4中曲线可知:粘聚力比值η在1.07左右,内摩擦角比值α在0.86~1.11之间变化,而文[11]中,Q2黄土的粘聚力比值在0.9~1.9之间变化,内摩擦角比值在0.7~1.15之间变化.
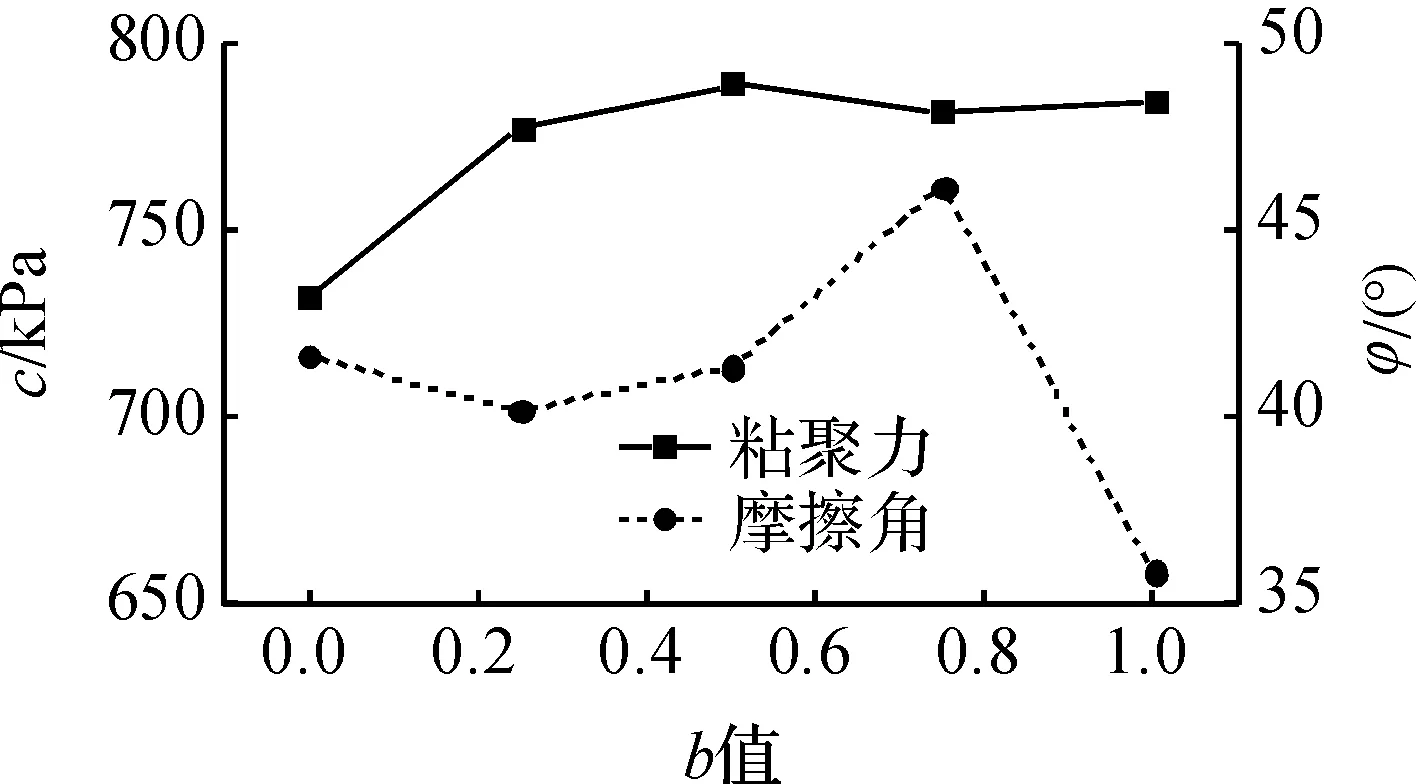
图3 强度参数与b值的关系曲线Fig.3 Curves of strength parameters versus intermediate principal stress ration b
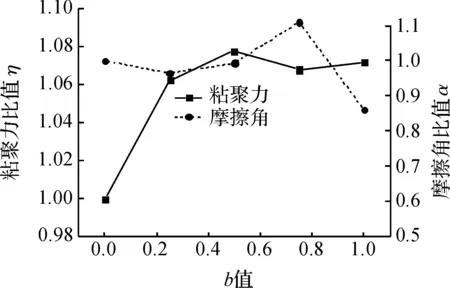
图4 强度参数比值与b值的关系曲线Fig.4 Curves of strength parameters ratio versus intermediate principal stress ration b
从中主应力作用面观察试验试样破坏形态时发现,本次试验中试样的破坏方式主要有三类,既锥形破坏、梯形破坏、六边形破坏,具体如图5,6所示,与文[11]相似.试验过程中并没有发现侧胀破坏现象,这是因为本次试验试样为重塑粘性土,含水率较低且强度较大,土的结构很难达到整体上的破坏,故未出现侧胀破坏.
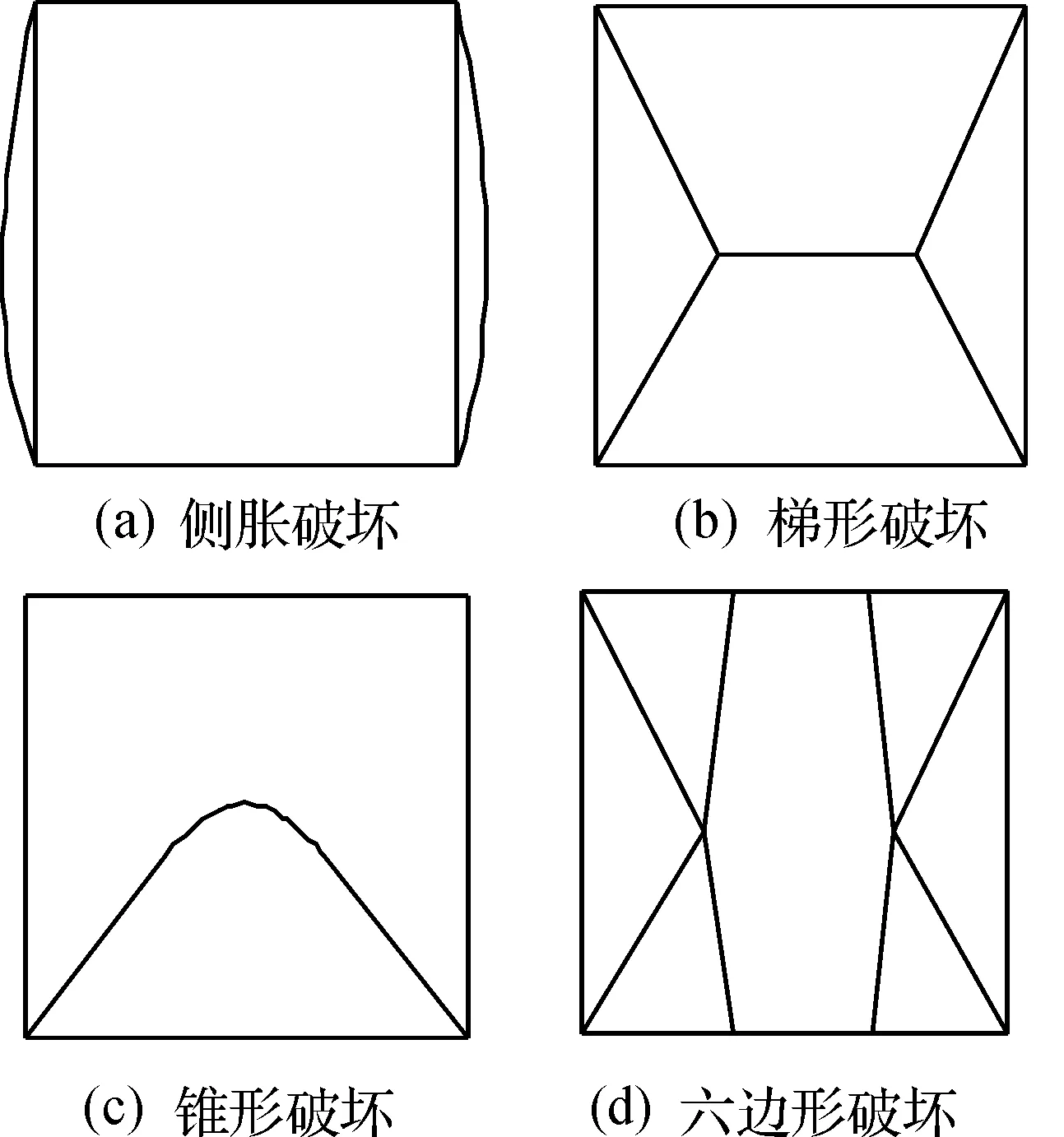
图5 试样破坏方式示意图Fig.5 Schematic diagram of the specimen failure mode

图6 试样破坏方式实物图Fig.6 The physical map of specimen failure mode
3屈服面分析
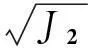

图7 各种b值下剪切破坏面拟合曲线Fig.7 The fitted curves of shear failure plane with intermediate principal stress ration b
Table 2The statistical table of fitted parameter of shear failure plane

b值拟合参数α/kPaθ/1030.000.3640.1720.250.3310.1390.500.2960.1290.750.2630.1421.000.3270.116
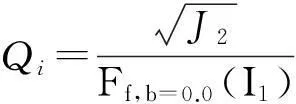

图8 比值Qi与应力张量第一不变量拟合曲线Fig.8 The fitted curves of the ratio Qiand the first stress tensor invariant
Table 3The statistical table of fitted parameter between the ratioQiand the first stress tensor invariant

b值拟合参数αiθi/(MPa)-10.500.800-8.59E-031.000.837-2.37E-03
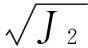
同时,引入了形状函数g(I1,θσ)(在Rubin函数中指缩放函数),因此其破坏函数可以统一表示为
(4)
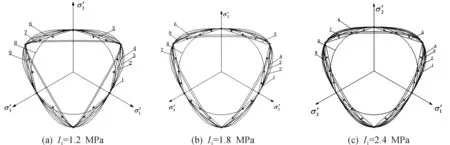
1—Gedehus和arygris;2—邢义川;3—Williamt和Warnke;4—郑颖人和陈瑜瑶;5—莫尔-库伦;6—Rubin;7—Lade和Duncan;8—Drucker-Prager;9—Matsuokd和Nakai图9 π平面上各种形状函数表示的破坏面Fig.9 The failure plane on deviatoric stress plane by shape functions
其中:I1为应力张量第一不变量;J2为偏应力张量第二部变量;J3为偏应力张量第三不变量;Ff,b=0.0(I1)为b=0时的剪切破坏面函数.形状函数g(I1,θσ)表示在π平面上屈服曲线随洛德角θσ和应力张量第一不变量I1的变化规律,其具体函数形式主要有莫尔-库伦,Drucker-prager,Willialns和Warnke,Gedehus和Arygris,Lade和Duncan,Matsuokd和Nakai,Rubin,郑颖人和陈瑜瑶、刑义川等.以下仅就Rubin函数作简单介绍:
Rubin考虑用二次函数曲线来表示在π平面上介于三轴压缩和三轴拉伸屈服点之间屈服曲线,其形状函数[15]为
(3)

利用表3中的参数计算出I1=1.2,1.8,2.4MPa对应的Q1和Q2值,同时根据所得的Q1和Q2值将不同的形状函数表示的破坏函数绘制在π平面上,具体结果见图9.
从图9中可知:数据点与莫尔-库伦准则和Rubin提出的形状函数逼近程度最好,而Lade和Duncan,Matsuokd和Nakai准则描述的破坏面与数据点有较大的误差,并且随着应力张量第一不变量的增加,由Willialns和Warnke,Gedehus和Arygris,Rubin,郑颖人和陈瑜瑶、刑义川提出的破坏函数在π平面上的差值逐渐减少,考虑到Willialns和Warnke,Gedehus和Arygris,郑颖人和陈瑜瑶、刑义川等提出的形状函数是根据拉压强度比值来确定,而Rubin提出的形状函数是根据三轴扭转(b=0.50)和拉压强度(b=1.00)的比值来确定,同时Rubin函数能够克服莫尔-库伦函数存在的一阶不连续点而造成的数值计算不收敛等困难和通过参数的选择可以变换到其他形状函数,因此其灵活性更大,适用面更广[18].
4结论
通过本次在不同最小主应力和中主应力系数b条件下的真三轴试验,分析了其应力—应变曲线的变化规律、中主应力系数b对其峰值应力和峰值应变、抗剪强度参数的影响以及试件破坏方式,在此基础上同时引入形状函数,并对不同形状函数进行了研究.结果表明:不同最小主应力下,峰值偏应力随b值增加表现出先增加而后减少的趋势,而最小主应力为其他值时,在b=0.75时达到最大值,而峰值应变随b值的变化规律恰好与峰值前曲线的变化率和峰值偏应力相反,其随b值的增加表现出先减小而后增大的趋势;内摩擦角φ13随b值的增加先增加而后减小,在b=0.75时达到最大;粘聚力c13先随b值的增加而增加,但当b≥0.25后基本上变化不大;数据点与莫尔-库伦准则和Rubin提出的形状函数逼近程度最好.
致谢:感谢西安理工大学岩土工程研究所的邵生俊教授及其研究生王桃桃在试验和数据处理过程中给予的支持和帮助.
参考文献:
[1]王智猛.红层泥岩及其改良土填筑高速铁路路基适应性及工程技术研究[D].成都:西南交通大学,2010.
[2]刘俊新,胡启军,邱恩喜,等.西南红层工程特性及其路堤稳定性[M].北京:科学出版社,2013.
[3]孙红,袁聚云,赵锡宏.软土的真三轴试验研究[J].水利学报,2002,46(12):74-78.
[4]迟明杰,李小军,周正华,等.中主应力对砂土强度影响的细观机制研究[J].岩土力学,2010,31(12):3751-3757.
[5]LADE P V, DUNCAN J M. Cubical triaxial tests on cohesionless soil[J]. Journal of Soil Mechanics and Foundation Engineering Division, ASCE,1973,99(10):783-812.
[6]CHU J, LO S C R, LEE I K. Strain softening and shear b and formation of sand in multi-axial testing[J]. Geotechnique,1996,46(1):63-82.
[7]CALLISTO L, CALABRESI G. Mechanical b ehavior of a natural soft clay[J]. Geotechnique,l998,48(4):495-513.
[8]吕玺琳,黄茂松,钱建固.真三轴状态下砂土的强度参数[J].岩土力学,2009,30(4):981-984.
[9]扈萍,黄茂松,马少坤,等.粉细砂的真三轴试验与强度特性[J].岩土力学,2011,32(2):465-470.
[10]王桃桃.新型真三轴仪改进及饱和砂土力学特性测试分析[D].西安:西安理工大学,2010.
[11]于清高,邵俊生,佘芳涛,等.真三轴条件下Q2黄土的破坏模式与强度特性研究[J].岩土力学,2010,31(1):66-70.
[12]邓国华.真三轴条件下黄土的结构性参数及结构性本构关系研究[D].西安:西安理工大学,2009.
[13]罗爱忠.新型真三轴仪调试及重塑黄土强度变形特性的试验研究[D].西安:西安理工大学,2008.
[14]邵俊生,罗爱忠,邓国华,等.一种新型真三轴仪的研制与开发[J].岩土工程学报,2009,31(8):1172-1179.
[15]RUBIN M. Simple convenient isotropic failure surface[J]. Journal of the Engineering Mechanics Division, American Society of Civil Engineers,1991,117:348-369.
(责任编辑:刘岩)
中图分类号:TU41
文献标志码:A
文章编号:1006-4303(2015)03-0283-05
作者简介:刘俊新(1976—),男,江西安福人,博士后,主要从事岩土工程与防护工程研究,E-mail:ljx0614@126.com.
基金项目:国家自然科学基金资助项目(51234004,41272297);四川省科技支撑计划项目(2013GZ0071);国际合作项目(2014HH007)
收稿日期:2014-12-05

