架空导线用钢芯铝绞线张力分层特性研究

林建华，曾 伟

(1.广东电网公司东莞供电局，广东 东莞523000;2.上海电缆研究所，上海200093)

0 引言

钢芯铝绞线(ACSR)是架空绞线主要产品之一，具有结构简单、架设与维护方便、线路造价低、传输容量大等特点，因此在各种电压等级的架空输配电线路中得到广泛应用。典型的钢芯铝绞线内部是镀锌钢芯线，外部是由单层或多层铝股线绞合在钢芯周围，其结构如图1所示。钢芯铝绞线在运行过程中，钢芯和铝股共同承担张力，但因ACSR结构特殊，各层单股的应力分布并不是均匀的，若运行过程中产生应力集中则会导致断股，如图2所示，这将严重影响输电线路的安全运行。

图1 钢芯铝绞线示意图

本文主要针对钢芯铝绞线的结构特点，采用ABAQUS软件建立ACSR的几何模型，确定模型的边界条件，模拟在导线实际运行过程中受张拉力时，各层单线所受到的沿导线轴向方向的纵向力和各铝线层的应力分布情况。虽然钢芯铝绞线在大气中可能受水分、化学气体和盐类物质等侵蚀介质的作用发生腐蚀，导致导线明显变脆，抗拉强度大幅降低，严重时也会造成断股、断线，但本文中暂不考虑化学腐蚀对ACSR的性能影响。

图2 钢芯铝绞线断股

1 基本力学性能

钢芯拉断时延伸率为2%～4%，而铝线股拉断时的延伸率仅为1%～2%，因此钢芯铝绞线拉断前总是铝线先被拉断，而此时的钢芯仍工作在其弹性阶段。由于钢芯铝绞线是两种线材分层同轴绞绕制成的柔索，构成绞线的单线都是螺旋线，当绞线受到张拉时不仅沿自身轴向伸长，而且各层之间也相互挤压。为了量化导线在受到张拉力时所受的应力，可通过建立单线纵向力和各层之间挤压力的控制方程，推导出应力的计算方法。应力计算模型的建立必须满足以下两点假设:

(1)同层股线受力状态相同，且各股线的轴心线位于同一圆柱面内;

(2)各股线的螺旋升角变化微小。

2 导线的应力-应变物理方程

图3为导线第i层某股线的受力示意图，绞线沿轴线方向的纵向力用pi表示，在其作用下横截面上的内应力为:轴向应力Nip=pisinαi;剪切应力Qip=picosαi;弯矩Mip=－piRisinαi;扭矩Tip=piRicosαi。

层间均匀分布的挤压力用qi表示，该力作用在绞线横截面上所产生的内应力如图4所示。

从图4看，轴向应力Nip=qiRi;剪切应力Qip=－qiRitanαi;弯 矩Mip=－qi扭 矩Tip=－qitanαi。

3 有限元模型

钢芯铝绞线是由一根或多根钢芯周围螺旋绞上一层或多层单线组成的，其相邻层绞向相反。根据ACRS 720/50架空导线的绞制特点，可利用CATIA软件生成各单线的母线，再拉拔出几何模型，之后将几何模型导入ABAQUS建立有限元模型。模拟导线在张力作用下的运行条件，建立其应力、应变分析的边界条件，确立合理的分析类型和计算模式，利用ABAQUS软件强大的有限元分析功能进行数值模拟，获得导线的张力分层特性。

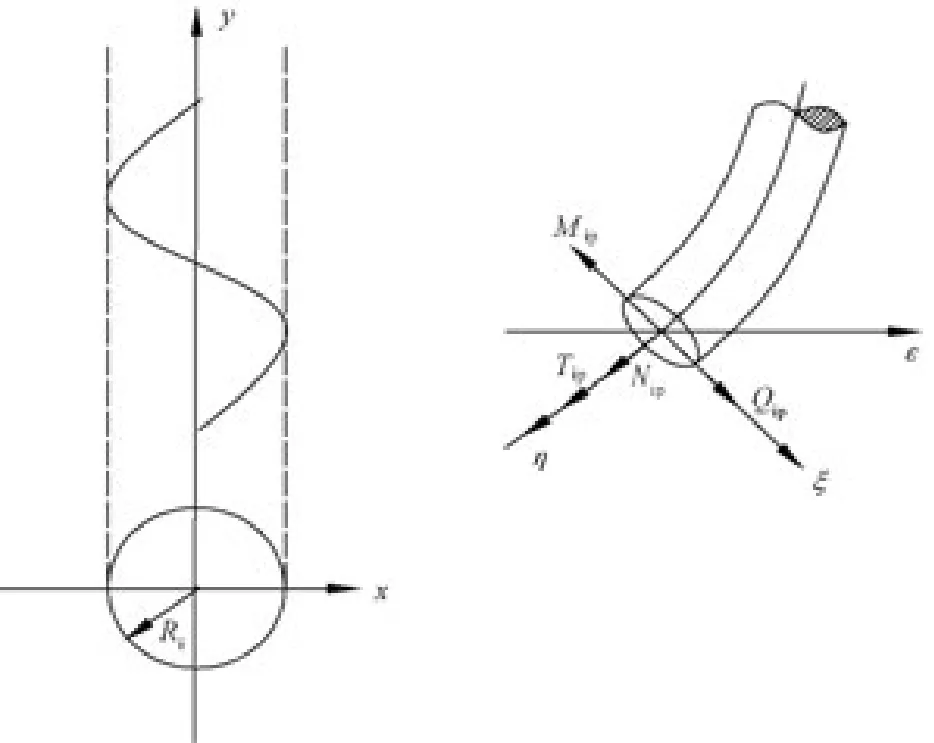
图3 单绞线在纵向力作用下的内应力

图4 单绞线在径向力作用下的内应力

3.1 建立几何模型

以ACRS 720/50架空导线为例，几何参数如表1所示。假设每股单线为螺旋的细长圆柱体，利用CATIA软件按照ACRS 720/50架空导线几何参数建立几何模型，再导入ABAQUS软件进行建模。

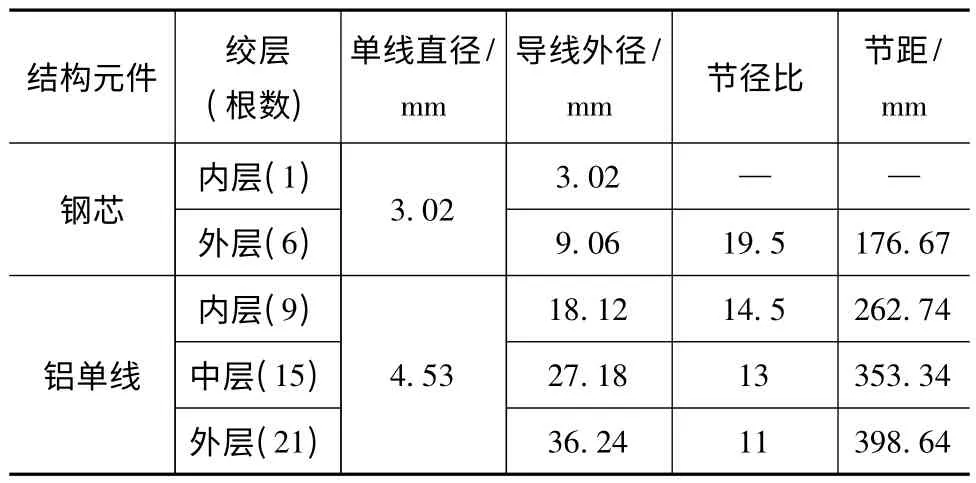
表1 ACRS 720/50架空导线的几何参数

3.2 材料参数

钢芯铝绞线由钢芯外包铝线绞合而成，模型中各材料均假设为连续、均质、各向同性，钢芯、铝线可假设为线弹性材料，即应力应变关系在弹性范围内为线性的。弹性模型是基于广义虎克定律建立的，模型采用各向同性材料，弹性模量E、泊松比v、剪切模量G三个材料参数只有两个是独立的，一般按弹性模量E、泊松比v取值，见表2。

表2 材料参数

3.3 边界条件

根据架空导线承受轴向拉力时的实际情况，架空导线受力问题属于大转动小应变几何非线性弹塑性问题。在架空导线有限元模型上z=0端面约束柱坐标y、z两个方向的自由度，z轴另一端面约束柱坐标y方向的自由度，按10%RTS(额定拉断力)，即17.06 kN施加载荷，并耦合该端面上节点的自由度。

3.4 网格划分

通过网格划分，ACRS 720/50架空导线几何模型成为有限元模型，合适的单元形状和数目是十分重要的。粗劣的单元形状会影响分析结果的准确性，单元的数目多少直接影响计算的精度，单元的数目多，可以提高计算的精度，但是运行时间长，效率较低。在划分单元时，应在满足计算结果精度的要求下，尽可能地提高计算效率。考虑到导线模型的计算长度过长会影响计算速度，因此本模型的长度取为30 mm。利用C3D8R(8节点六面体线性减缩积分单元)对导线进行网格划分，导线有限元模型如图5所示。

图5 钢芯铝绞线有限元模型

4 计算结果与讨论

Von Mises等效应力是指在复杂应力状态下，基于剪切应变能的一种等效应力，等效应力的数值与屈服应力一样，其大概含义是当单元体的形状改变比能达到一定程度，材料开始屈服。因此采用等效应力作为衡量导线应力水平的主要指标。

4.1 单股应力分布

导线各股线因其分层结构而在运行过程中承受不同的张力值，同层个股线受力情况大体一致。分别取钢芯外层和铝股内层、邻外层、外层其中一股，轴向应力、剪切应力、等效应力的数值及变化规律，如图6所示。

从图6中可以看出:(1)单股的等效应力最大值位于与外层的接触区域，且离端面越近，应力越大;(2)单股弯曲外侧受拉，内侧受压;(3)导线单股上存在剪切应力。由于各个绞层的外径和节径比不同，不同单股曲率半径的不同，加上层间的挤压力对剪切应力的影响，铝股剪切应力由内层到外层逐渐减小。相对于铝股的剪切应力，钢芯外层剪切应力较大。

4.2 导线应力分布

建立钢芯铝绞线的参考点，并将导线左端与参考点进行耦合，对参考点施加17.06 kN的载荷，图7为加载后导线的等效应力分布情况。由图7可以看出，在轴向拉力的作用下，导线外层铝线受拉，邻内层和内层铝线外层由于绞合弯曲形成了沿径向的挤压力。与钢芯接触区域应力值显著增加，且在截面上分布不均。

图7 钢芯铝绞线等效应力分布图

钢芯的单股应力要大于铝股，其中直股钢芯的应力值最大，验证了钢芯铝绞线结构上分工特点，钢芯主要承担张力;铝股应力值外层依次大于邻内层。此外，由于外层股线没有沿径向的挤压力，外层股线应变比内层大。越靠近约束端面(假设有吊线夹固定的端面)，铝股外层和邻外层的等效应力受端面约束力的影响越大，这是由于架空导线端面处的约束力是沿着Z轴方向，与各铝股的延伸方向存在一定的夹角。

5 结论

根据钢芯铝绞线的结构、材料特性和绞制特点，结合导线在实际运行过程中的强度设计要求，利用ABAQUS软件建立了导线各层股线有限元模型，模拟导线在运行过程中所受张拉力后的应力分布规律。

(1)对计算结果的分析表明，当导线承受张拉力时，各层股线除了沿其自身轴向伸长之外，各层间还将相互挤压。由于外层股线没有沿径向的挤压力，外层股线应变比内层大。外层铝股受力要依次大于相邻内层，这与导线的组成结构及实际断股事故的发生情况相符合，表明所建立的分层力学模型合理。

(2)初步研究表明，导线在线夹出口处的受力较复杂，且等效应力受端面约束力的影响较大，在导线覆冰和振动过程中，容易造成导线与线夹接触处的疲劳断股。因此，在安装导线时应重点保护线夹出口处导线。

导线的力学性能和强度设计直接关系到输电线路的可靠性和电网的安全运行，本文通过对导线不同层股线的载荷与应力分布研究，结合线路的电压等级、输送能力、强度、寿命、环境影响、经济性等多方面的因素，可以对导线的力学性能进行准确的分析和计算校核，以满足不同需要及外界条件的需求，也可作为导线优化设计和合理选择的参考。

［1］张殿生.电力工程高压送电线路设计手册(第二版)［M］.北京:中国电力出版社，2003.

［2］邵天晓.架空送电线路的电线力学计算(第二版)［M］.北京:中国电力出版社，2003.

［3］Chen Guohong，Wang Xu，Wang Jiaqing，et al.Damage investigation of the aged aluminium cable steel reinforced(ACSR)conductors in a high-voltahe transmission line［J］.Engineering Failure Analysis，2012(19):13-21.

［4］Azevedo C.R.F，Cescon Failure T analysis of aluminum cable steel reinforced(ASCR)conductor of the transmission line crossing the Parana River［J］.Engineering Failure Analysis，2002，9(6):645-664.

［5］Barrett S.J，Motlis Y.Allowable tension levels for overhead-line conductors［J］.IEE Pro-Gener，Transm.Distrib，2001，148(1).

［6］Franc Jakl，Menber，IEEE and Andrej Jakl.Effect of elevated temperatures on mechanical properties of overhead conductors under steady state and short-circuit conditions.IEEE Transactions on power delivery，2000，15(1).

［7］Muhr Michael，Pack Stephan，Jaufer Stefan.Elongation of overhead line conductors under conbined mechanincal and thermal stress.Internation conference on condition monitoring and diagnosis，2008.

［8］郑黎阳，孙祖志.铝绞线和钢芯铝绞线的应力分析［J］.武汉水利电力大学学报，1997，30(3):65-68.

［9］蔡斯特，倪海云，芮晓明.张力分层特性在架空导线强度上的应用研究［J］.南方电网技术，2009，3(S1):48-50.

［10］石亦平，周玉蓉.abaqus有限元分析实例详解(第一版)［M］.北京:机械工业出版社，2006.

［11］曹金凤，石亦平.ABAQUS有限元分析常见问题解答(第一版)［M］.北京:机械工业出版社，2006.