基于ENTROPY-TOPSIS法的多式联运方案研究

刘基良，刘名武，卢 旭

（1.西南民族大学 预科教育学院，四川 成都 610041；2.重庆交通大学 管理学院，重庆 400074）

1 引言

多式联运具有其他运输组织形式无可比拟的优越性，已在我国得到广泛的推广和应用。由于多节点、多运输方式以及多路径组合方案众多，如何进行运输方式与运输路线选择，成为多式联运研究的主要问题。

多式联运运输方式、运输路线的选择已有不少成果。苏印等[1]把运输费用、运输时间以及运输质量作为多式联运最关键的三个因素，并运用层次分析法来选择多式联运的线路。贺竹罄等[2]结合多种运输方式的技术经济特点，以运输费用最小化为目的，建立了多式联运方式选择的整数规划模型。刘舰等[3]运用图论技术构建基于多种运输方式的运输网络，并提出基于克隆增广的人工免疫求解算法。康凯等[4]采用主从混合智能启发式方法，构建运输方式和运输路径优化集成模型，解决了运输网络多节点、多方式、多路径的集成优化问题。本文则构建了基于ENTROPY-TOPSIS法的多式联运方案选择模型，解决权重分配和最优方案选择问题，提供一种新的多式联运方案选择方法。

2 多式联运方案选择指标体系构建

多式联运方案选择受到多种因素的影响，本文考虑以下因素：

（1）运输成本。运输成本是指货物在途运费加上提供额外服务的所有附加费用。它对运输方式与运输路径的选择起决定性作用。在考察运输成本时，要依据总成本的概念，综合考虑运费、中转费、装卸费以及仓储费等。

（2）运输时间。运输时间是指货物从起点运输到讫点所耗费的平均时间。它不仅包括各段的运输时间，还包括中转点的中转时间以及必要的仓储时间。

（3）可靠性。运输的可靠性是指采用同种运输方式下多次运输出现的时间变化。因为天气、交通情况以及中途经停次数等的不同，即使是起讫点相同、运输方式与路线相同的每一次运输的时间也不一定相同，一般用平均运输时间的方差或者标准差来衡量运输服务的稳定性。

（4）安全性。安全性主要是指货物在运输途中有没有损坏或者灭失。在运输途中，由于天气、路况以及海浪等不可抗力会使得货物或多或少的遭受损坏。不同运输方式和路径对所载货物的安全性影响也不同，可以用所承载货物的损坏率来衡量运输方式的安全性。

（5）碳排放量。主要包括在运输过程、转运过程以及装卸过程中的碳排放当量。本文选取易量化的碳排放量来反映运输方式与路径的选择对大气的污染程度。

3 基于ENTROPY-TOPSIS法的评价模型

3.1 应用ENTROPY确定评价指标权重

基于信息论的ENTROPY 法，在确定指标权重时，通过各指标传输给决策者的信息量大小来决定，从而确定分布规律以及变化范围。假设m个备选运输方案的n个指标评价值为xij，i为备选方案，j为第j项指标，建立初始矩阵：

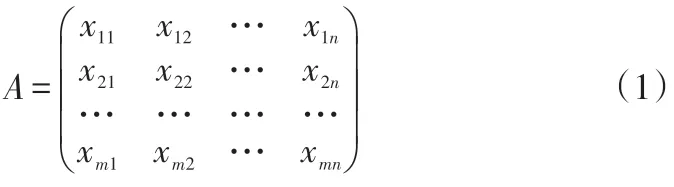
对决策矩阵A进行规范化处理：

利用信息熵计算各指标的熵权。熵是物理学上的概念，在信息理论中用概率来衡量信息的不确定性。信息熵越大说明数据的分布越分散，不确定性越大。设第j个指标的信息熵为：

第j个指标的熵权dj定义为：

若为深部地热上涌与临近断层活动引起的，那么井水温度应该为渐变型上升，与本次异常情况不符，因此排除此种可能性。

对dj进行归一化处理，获得评价指标的标准化权重：

3.2 应用TOPSIS模型对方案进行排序

TOPSIS 法是Hwang 和Yoon 在1981 年提出来的有效多属性决策方法。这种方法的基本原理是被选方案应该距离理想解最近同时又远离负理想解。假设每一属性是单调的，可以将偏好转化成欧式距离加以计算与衡量，经过综合比较选择最佳方案。

由归一化矩阵R与各指标的熵权wj相乘得到加权评价值矩阵：

确定理想解S+和负理想解S-：

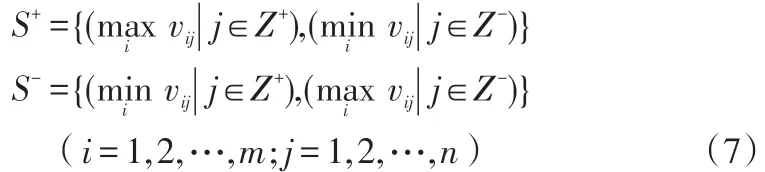
其中，Z+为效益型的指标，Z-为成本型的指标。分别计算各方案到理想解和负理想解的欧式距离：

分别计算各方案与理想解的相对接近度：

依据ηi(0 ≤ηi≤1)的值对各运输方案进行排序。

4 算例分析

算例1：以1t 货物从四川达州经由重庆万州运往上海为例，可行的运输方案有四种：公水联运、铁水联运、公路直达以及铁路直达。原始数据见表1。采用本文提出的评价模型与方法对它们进行评价与选择。

表1 1t货物从达州到上海的相关数据（以万州为节点）

根据表1 的数据，使用ENTROPY 法确定各指标的权重，结果见表2。

表2 指标信息熵值、熵权以及标准化权重

然后对归一化的数据进行加权处理，并将破损率归为效益型指标，运输费用、运输时间、运输时间变化率归为成本型指标，则S+={0 .008 7,0.010 4,0.000 8,0.011 6,0.023 4} ，S-={0.209 9,0.032 5,0.001 1,0.006 1,0.409 2}。再计算各方案与理想解的相对接近度，结果见表3。

表3 货物从达州到上海（以万州为节点）运输方式评价结果

由表3可以看出1t货物从四川达州运往上海，其中铁水联运的方案最优，其次是公水联运以及铁路直达，公路直达的方案最差。

算例2：以1t 货物从四川成都运往上海为例，其运输路线有多种，可供选择的路线如图1所示。

图1 成都到上海可选择的路线

为了后续讨论的方便，表4列出了所有的可行运输方案。值得注意的是，由于算例1已经对达州到上海段进行了讨论，得出公路直达方式与其它三种相差甚远，故本算例没有考虑达州经万州到上海的公路直达运输方案。

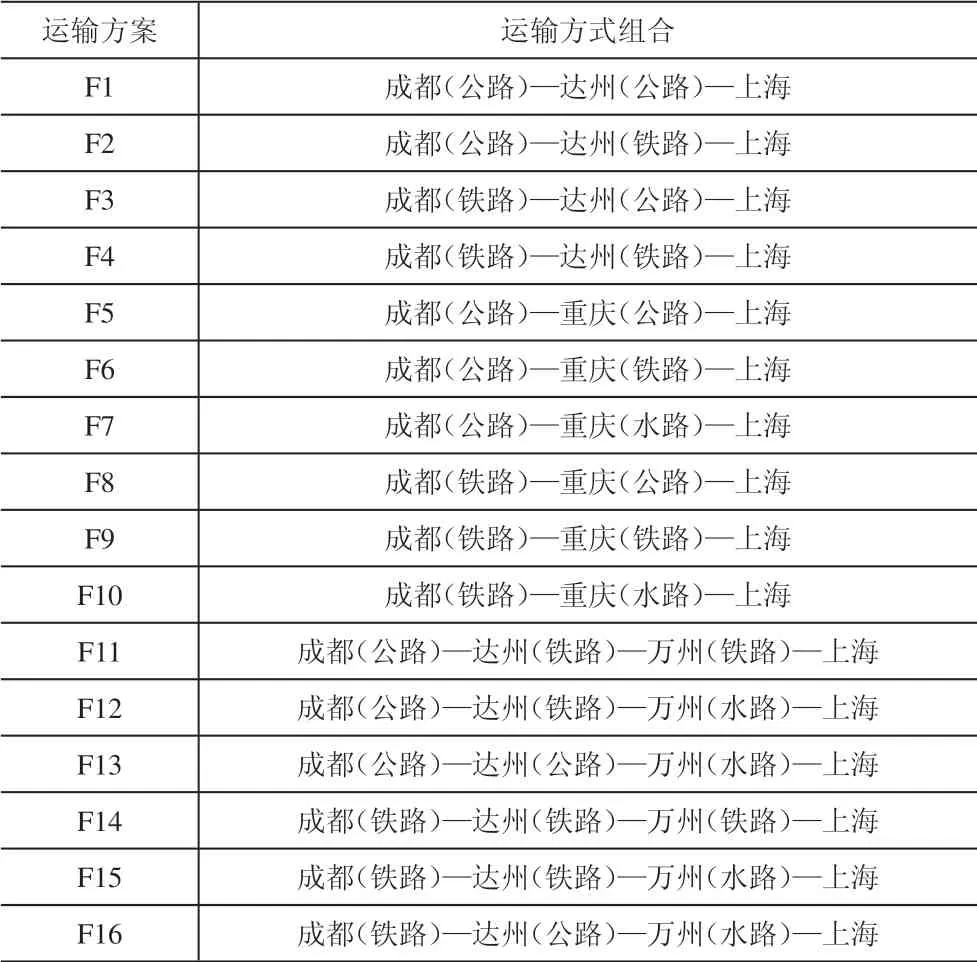
表4 1t货物从成都到上海的运输方案

各运输方案的原始数据见表5。

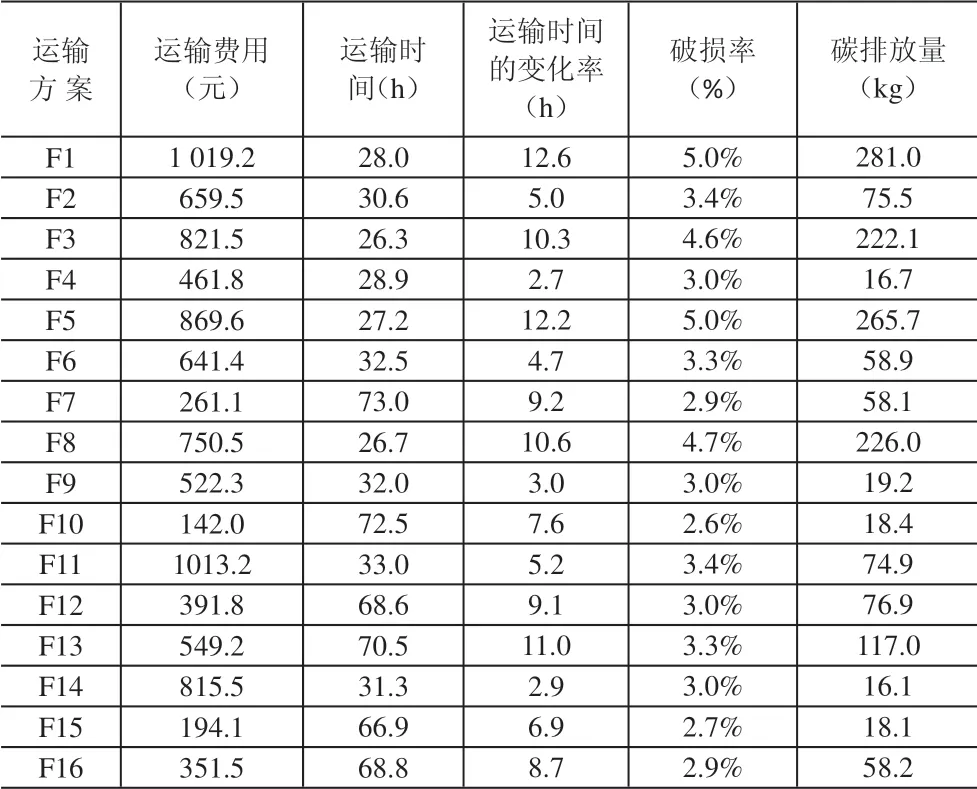
表5 1t货物从成都到上海各方案原始数据

按照ENTROPY法计算各指标的权重。计算结果见表6。

表6 相关指标的信息熵值、熵权以及标准化权重

类似算例1，得到理想解S+和S-分别为：S+={0 .002 3,0.004 9,0.002 9,0.003 2,0.005 4} ，S-={0.016 7,0.0137,0.013 7,0.001 6,0.095 2}。计算各方案与理想解的贴近度，从而得各方案的排名，结果见表7。

表7 1t货物从成都到上海各方案综合排名

从表7可以发现：1t货物从成都运往上海排名前三的运输方式分别是：（1）铁路直达经由达州运到上海；（2）铁路直达经由重庆运到上海；（3）先由铁路经过达州运到万州，再从万州走水路运到上海。

一般来说，大宗货物运输由于地质以及装载量的限制，使得长距离的货物运输选择公路直达这种运输方式就不是太方便。从表7中不难发现公路直达的运输方式基本都排在了最后，而排在靠前的运输方案中只有短距离运输（如方案6从成都到重庆以及方案16从达州到万州）才选择了公路运输。另外像成都到上海大宗货物长距离运输大多以铁路为主，可以在不同的节点装载该地的丰富资源运往东部沿海城市。还有一个值得关注的是方案15，从万州通过水路运往上海，正好契合依托黄金水道建设长江经济带的发展要点，具有较强的现实意义。

5 结束语

本文研究了多式联运运输方式和运输路径的组合选择问题。首先，构建指标体系，融入了运输的可靠性以及碳排放量两项指标，使得指标体系更加符合低碳运输的要求。然后，采用ENTROPY-TOPSIS法计算各指标的权重以及对不同的运输方案进行排序，一定程度上克服了以往方法中主观性强的缺陷。最后，算例表明本文提出的方法有效且得出的结果比较满意。

[1]苏印,李铁柱.国际多式联运线路选择的方法研究[J].交通运输系统工程与信息,2006,6(2):91-94.

[2]贺竹罄,孙琳岩,李晓宏.时效性物流联运方式选择模型及其算法[J].管理科学,2007,20(1):8-12.

[3]刘舰,俞建宁.多式联运运输方式选择的模型和算法[J].兰州交通大学学报,2010,29(1):56-61.

[4]康凯,牛海姣,朱越杰,张维存.多式联运中运输方式与运输路径集成优化模型研究[J].计算机应用研究,2010,27(5):1 672-1 675.

[5]沈志军,杨斌.考虑碳排放下的集装箱物流运作策略研究[J].武汉理工大学学报,2012,34(5):70-75.

[6]朱晓宁,席江月.基于熵权-TOPSIS的城际铁路客运站选址研究[J].铁道运输与经济,2013,35(10):32-36.

[7]尹航,李柏粥,郭韬.基于Entropy-Topsis模型的产品创新过程分析与实证检验[J].运筹与管理,2013,22(5):185-195.