有理重心插值中Lebesgue函数的最值性质

张善奎，朱方妍，邓重阳

(杭州电子科技大学理学院，浙江 杭州 310018)



有理重心插值中Lebesgue函数的最值性质

张善奎，朱方妍，邓重阳

(杭州电子科技大学理学院，浙江 杭州 310018)

摘要：Floater和Hormann提出的有理重心插值具有很好的性质，在逼近论及相关领域中有重要的应用。Floater和Hormann插值函数中，Lebesgue常数反映了有理插值的稳定性，d决定着有理插值的权重系数和插值进程的好坏。当d=2时，证明了插值节点等距时，其对应的Lebesgue函数的最大值在区间的两个端点处取到。

关键词：有理重心插值；Lebesgue函数；逼近

0引言

Floater和Hormann提出的重心有理插值既避免了多项式插值可能出现的龙格现象[1]，又弥补了一般有理插值在控制极点产生上的不足[2]，因而广泛应用于逼近论及相关领域。有理插值对应的Lebesgue函数在区间[a,b]上的最大值称为Lebesgue常数[3]，它反映了有理插值的稳定性。文献[4]研究了等距节点下Floater-Hormann有理重心插值的Lebesgue常数的上界和下界,给出的图形表明，对于不同的d，Lebesgue函数取得最值的点所在的区间也不一样。当d=0及d=1时，Lebesgue函数在[a,b]的中点或中点附近取得最值。当d≥2时，Lebesgue函数在[a,b]的区间的两端取得最值，并且随着d值的增大，Lebesgue函数在两个端点处取得最值的趋势越明显，但文献[4]没有从理论上证明这一现象。本文证明了当d=2时，Floater和Hormann重心有理插值所对应的最大值确实能在区间的两个端点处取到。

1主要结果

Floater-Hormann有理重心插值[5]的基函数为：

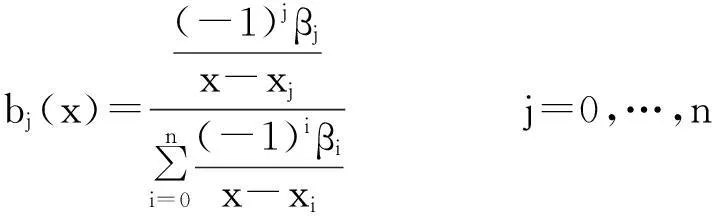
(1)

相应的Lebesgue函数Λn(x)定义为：

(2)

考虑到对称性，假定 k≤[n/2]-1,其中[x]代表不超过x的最大整数。

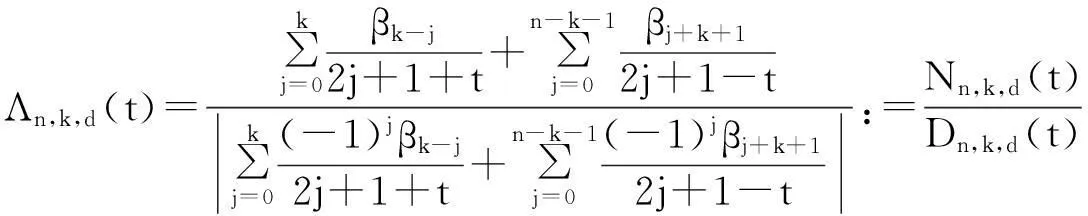
(3)

文献[2]证明了式(3)没有奇点，也就是说，Dn,k,d(t)>0。

对于d=2，有：

定理1当d=2且k是正偶数时，Λn,k+1>Λn,k并且Λn,k+2>Λn,k。

当k 和n都是偶数时，g1(t)<0，同样有 Λn,k+1(t)>Λn,k(t)。

所以，对于偶数k，对任意的n，都有Λn,k+1(t)>Λn,k(t)。类似地可以证明，k是偶数时，Λn,k+2>Λn,k。证毕。

定理2当d=2时，Floater-Hormann有理重心插值对应的Lebesgue函数在两个端区间上取得最值。

(4)

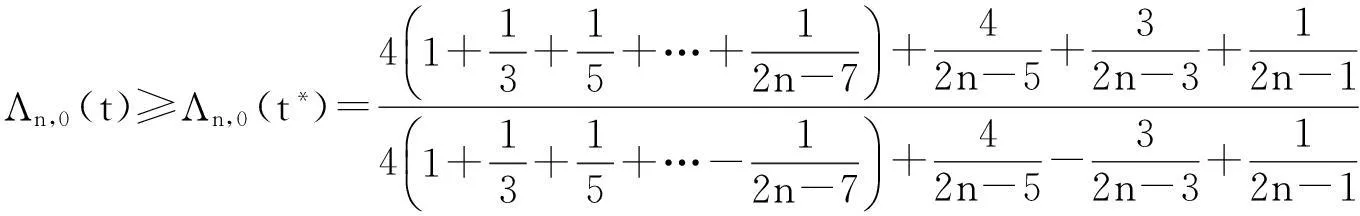
(5)

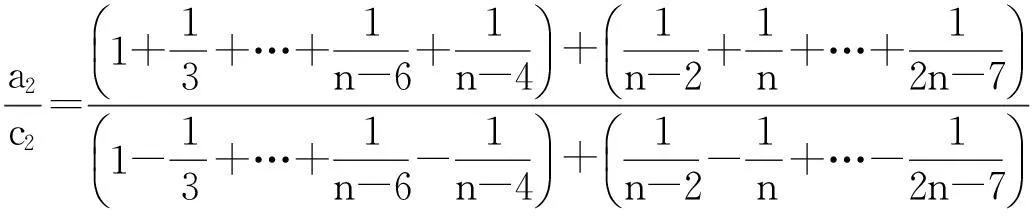
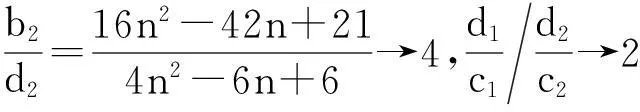
定理2得证。

2图形样例

d=2时，等距节点下的Floater-Hormann插值在n=9和n=10时的Lebesgue函数图像分别如图1(a)、图1(b)所示。

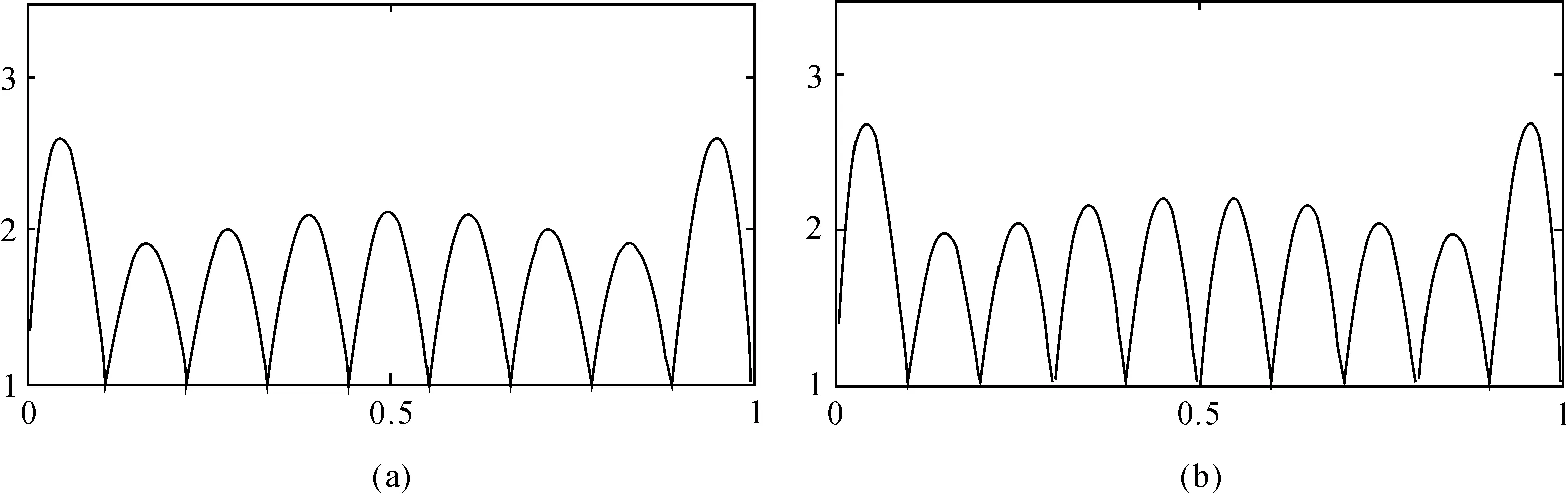
图1　d=2时,Lebesgue函数在n=9和n=10时的图像

从图1中看出，d=2时，不论节点n的奇偶性，Lebesgue函数的最值在区间的两个端点处取得，且单个子区间上的最值随着n值的增大而增大。除了端点外，Lebesgue函数在每个小区间上的最值又表现出渐增性，图形样例和理论证明吻合。

3结束语

有理重心插值中Lebesgue函数的最值决定着插值进程的稳定性，因此关于Lebesgue常数的求解问题显得尤为重要。本文从理论上证明了有理重心插值中Lebesgue函数的最值性质，用类似的方法可以证明当d≥2时，等距插值节点对应的Lebesgue函数都具有这个性质。

参考文献

[1] Brutman L.Lebesgue Functions For polynomial interpolation-a survey[J].Annals oF Numerical Mathematics,1996,4:111-128.

[2]Floater M S,Hormann K.Barycentric rational interpolation with no poles and high rates oF approximation[J].Numerische Mathematik,2007,107(2):315-331.

[3]Berrut J P,Baltensperger R,Mittelmann H D.Recent developments in barycentric rational interpolation[J].Trends and applications in constructive approximation.Birkhäuser Basel,2005,151:27-51.

[4]Bos L,De Marchi S,Hormann K,et al.On the Lebesgue constant oF barycentric rational interpolation at equidistant nodes[J].Numerische Mathematik,2012,121(3):461-471.

[5]Bos L,De Marchhi S,Hormann K.On the Lebesgue constant oF Berrut’s rational interpolation at equidistant nodes[J].Journal oF Computational and Applied Mathematics,2011,236(4):504-510.

The Property oF the Maximum on the Lebesgue Function oF

Barycentric Rational Interpolation

Zhang Shankui， Zhu Fangyan， Deng Chongyang

(SchooloFScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract:The Family oF barycentric rational interpolates introduced by Floater and Hormann not only gives better approximations than polynomial interpolation， but also cover the shortage oF controlling the occurrence oF poles For general rational interpolation. In the interpolation Function oF Floater and Hormann， d decides the weights and the properties oF interpolations. When d=2， we proved that the Lebesgue Function obtains its maximum at two endpoints oF the kont intervals．

Key words:barycentric rational interpolation; the Lebesgue Function; approximation

中图分类号：O241.3

文献标识码：A

文章编号：1001-9146(2015)03-0085-04

通信作者：

作者简介：张善奎(1988-)，男，河南信阳人，在读研究生，计算数学.邓重阳副教授,E-mail:dcy@hdu.edu.cn.

基金项目：国家自然科学基金资助项目(61370166)

收稿日期：2014-09-04

DOI:10.13954/j.cnki.hdu.2015.03.018