永磁同步电机的趋近律滑模控制

张宏达，贾贵玺，郭锦波， 杨 挺

(天津大学 智能电网教育部重点实验室， 天津 300072)



永磁同步电机的趋近律滑模控制

张宏达，贾贵玺，郭锦波， 杨 挺

(天津大学 智能电网教育部重点实验室， 天津 300072)

传统的交流伺服系统中速度环主要应用PI控制方式，虽然控制结构简单，可靠性强，但这种方法极易受到电机参数变化的影响，因此抗负载扰动能力差，鲁棒性不强。滑模变结构控制成功地克服了PI控制的上述缺陷，它通过不断改变系统的结构，使系统状态对负载扰动和电机参数的变化不再敏感，从而大大提升了系统的鲁棒性，有望被广泛应用于高性能的伺服系统中。采用id=0的矢量控制方案，在此基础上设计了指数趋近律的滑模控制，并用此方案替换了速度环常用的PI控制方案。最后利用仿真验证了此策略的可行性和优越性。

永磁同步电机；矢量控制；滑模变结构控制；趋近律；伺服系统

近30年来，随着各种高性能永磁材料的不断出现，尤其是20世纪80年代初第三代稀土永磁材料钕铁硼(Nd-Fe-B)的出现，永磁材料以其低廉的价格和优良的性能有力地推动了永磁电机的发展[1-2]。永磁同步电机具有结构简单、效率高、功率因数和功率密度高、体积小、易于散热及维护等特点[3-7]。

永磁同步电机的迅猛发展使得交流调速系统取代直流调速系统的脚步得以加快。永磁同步电机交流调速系统具有三环结构：外环位置环、内环速度环和电流环。速度内环的速度控制器普遍采用PI控制方式，当系统要求响应速度快、恢复能力强时，这种控制方式就有些力不从心。滑模变结构控制起源于20世纪50年代，其本质上是一种不连续的非线性控制。通过滑模控制，系统的自身结构不断变化，这恰恰能适应参数不断变化、负载扰动时有发生的交流调速系统。同时，滑动模态易于设计，且设计时与系统参数和扰动无关，因此滑模变结构控制具有对系统参数和外界扰动不敏感、响应速度快、实现简单等优点[8-20]。

滑模变结构控制最大的缺陷在于当系统的状态轨迹运动到切换面时，会产生不可避免的抖动现象，限制了滑模变结构控制的广泛应用。针对这一缺陷，学者们研究出许多削弱抖振的方法，例如采用准滑动模态的方法、观测器的方法、趋近律的方法、智能控制的方法以及动态滑模的方法等，这些方法都能在一定程度上削弱抖振现象，但都无法将其消除。

1 PMSM数学模型

永磁同步电机转子装有永磁钢，有些还装设阻尼绕组，定转子之间通过气隙磁场耦合。定转子间存在相对运动，各参量电磁耦合关系比较复杂，要想准确分析十分困难。为简化分析，本文假设：① 定子三相绕组对称，互差120°电角度；② 忽略磁路饱和以及涡流和磁滞损耗的影响，认为电机磁路是线性的；③ 定子感应电动势为正弦波，气隙磁动势按正弦规律变化；④ 不考虑阻尼绕组。在以上假设下，同步电机在d，q，o三相坐标系下的电压和磁链方程为：

同步电机转矩方程为

(3)

由id=iscosβ,iq=issinβ得

(4)

其中：Ld,Lq分别是直轴、交轴同步电感；Rs为定子电阻；Pn为定子绕组极对数；id,iq分别为在d，q，o三相坐标系中的直轴和交轴电流；TL为负载转矩；J为折合到电机轴上的转动惯量。

由式(1)～(4)可见：电机转矩包含励磁磁场与定子电流作用产生的电磁转矩和由于转子交直轴不对称而产生的转矩，即磁阻转矩。显然电机在d，q，o三相旋转坐标系下的数学模型将电机变系数微分方程变成了常系数方程，使分析运算简单了许多。

2 滑模控制器设计

2.1 滑模变结构控制

从本质上讲，变结构控制(VSC)是一种控制不连续的非线性控制，控制系统随时间变化不断改变自身结构，而传统的控制系统的结构是固定不变的。结构的变化若能启动“滑动模态”的运动，那么就称这样的控制为滑模变结构控制(SMC)。滑模变结构控制是变结构控制中最主流的设计方法。控制系统在该控制规律下被迫沿着规定的状态轨迹做高频小幅振动，即“滑动模态”运动。滑模变结构控制的优势在于：控制律的整定方法简单；滑模控制对系统参数变化不敏感；当扰动出现时，控制系统的响应和调整都很快，鲁棒性好。然而，当系统状态轨迹运动到滑模面s后，不能沿着滑模面滑动，而是在其两侧不断穿越趋近平衡点。由于惯性的原因，抖振现象不可避免，这也是滑模变结构控制存在的最主要的缺陷。

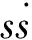
(5)

2.2 速度环滑模控制器设计

首先，确定永磁同步电机调速系统的状态变量x1，x2：

(6)

式(6)中：ω*是速度给定的，它是位置环控制器的输出；ω是电机转子的实际转速，将速度给定与实际转速比较后的结果作为速度环的输入信号。联合式(6)和转子的机械运动方程(4)可得：

(7)

(8)

写成状态空间表达式的形式为

(9)

设计滑模面s：

(10)

对式(10)中的s求偏导数得

(11)

结合式(9)和式(5)得

(12)

解得控制量iq的表达式为

(13)

得到的控制量iq作为给定的交轴电流送入电流内环。

2.3 稳定性验证

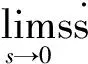
(14)

由于ε和k都是正常数，因此当s>0时，前面的负号保证了式(14)小于零;当s<0时，开关函数只为负，式(14)依然小于零，因此满足可达性和稳定性条件，保证滑模运动能在有限时间内到达切换面，且系统在指数趋近律滑模控制下渐进稳定。

3 仿真研究

本文采用id=0的矢量控制技术，按照图1所示的永磁同步电机调速系统的矢量控制系统，在Matlab中建立永磁同步电机调速系统仿真模型，包括速度环控制器、电流环控制器、Park变换与Clark变换、SVPWM调制、逆变器、电机状态方程、电机运动方程、Park 逆变换等几大模块。图5为基于PI控制器的速度环与电流环模型。

永磁同步电机参数设定如下：额定功率为10 kW，额定线电压U=380 V，频率f=30 Hz，极对数P=12，定子电阻R=1.25 Ω，直轴电感Ld=0.006 H,交轴电感Lq=0.019 H,摩擦因数B=0.191，转动惯量J=3.74，主磁极磁通为ψf=1.337。速度环用传统PI控制方式，在Matlab下开始进行仿真，模拟的速度响应波形、三相电流响应波形以及电磁转矩响应波形分别如图(2)～(4)所示。从速度响应曲线可以看出：转速大约在0.075 s时跟踪上给定转速，但存在一定的抖振和超调。从三相电流波形可以看出：三相电流波形有很大畸变；转矩波形在0.065 s时有很明显的跳变，之后稳定为100 N·m。

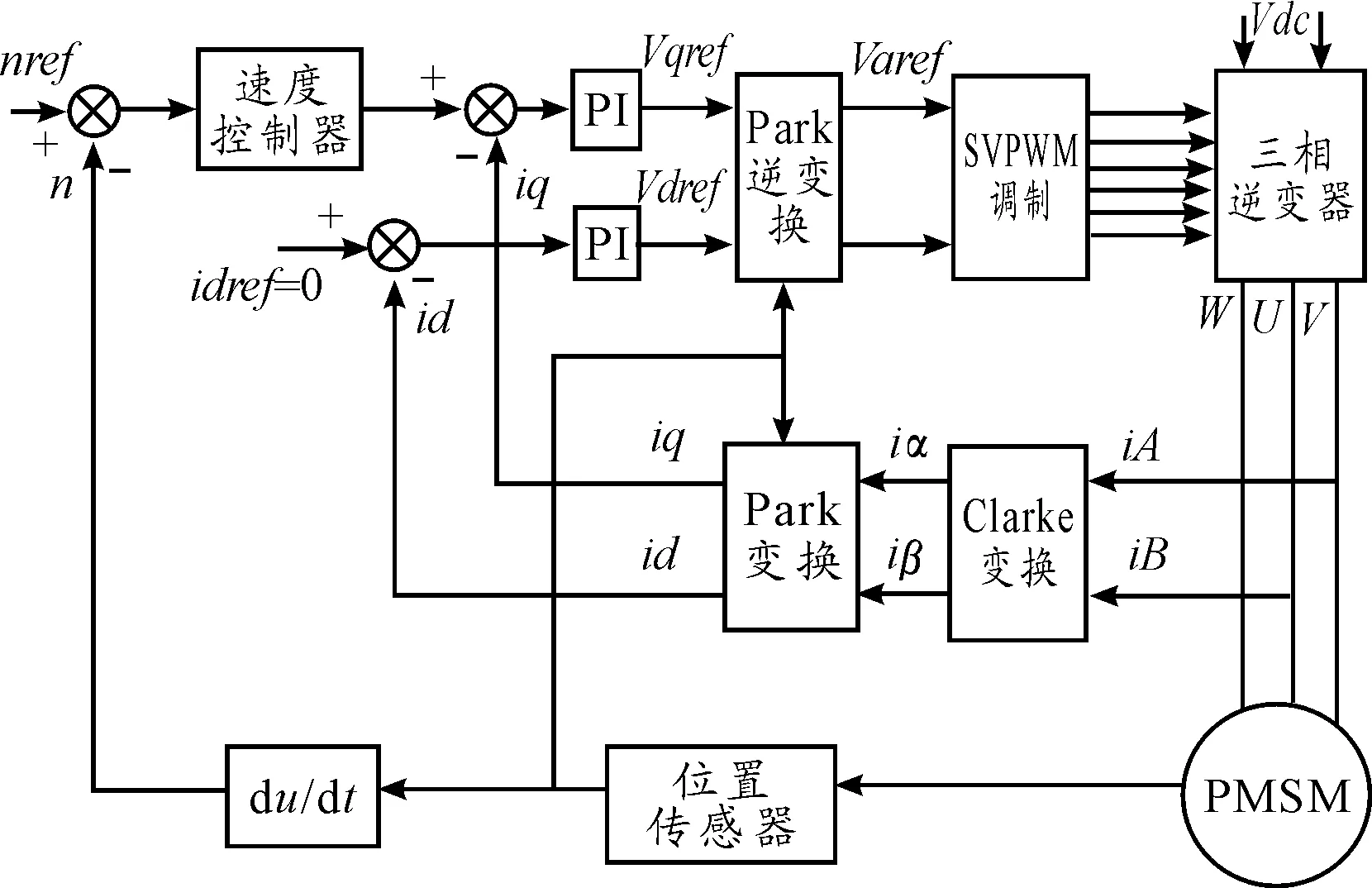
图1 永磁同步电机调速系统的矢量控制系统

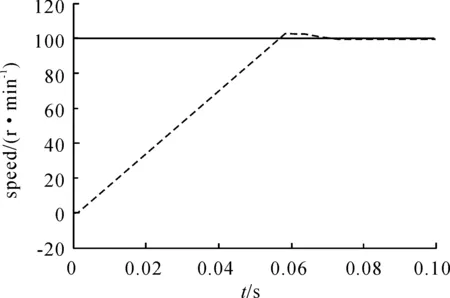
图2 速度响应曲线

图3 三相电流响应曲线

图5 速度环与电流环仿真模型

用设计好的指数趋近律滑模控制器替代速度环上的PI控制器，再次得到速度响应波形、三相电流响应波形以及电磁转矩响应波形，分别如图(6)～(8)所示。

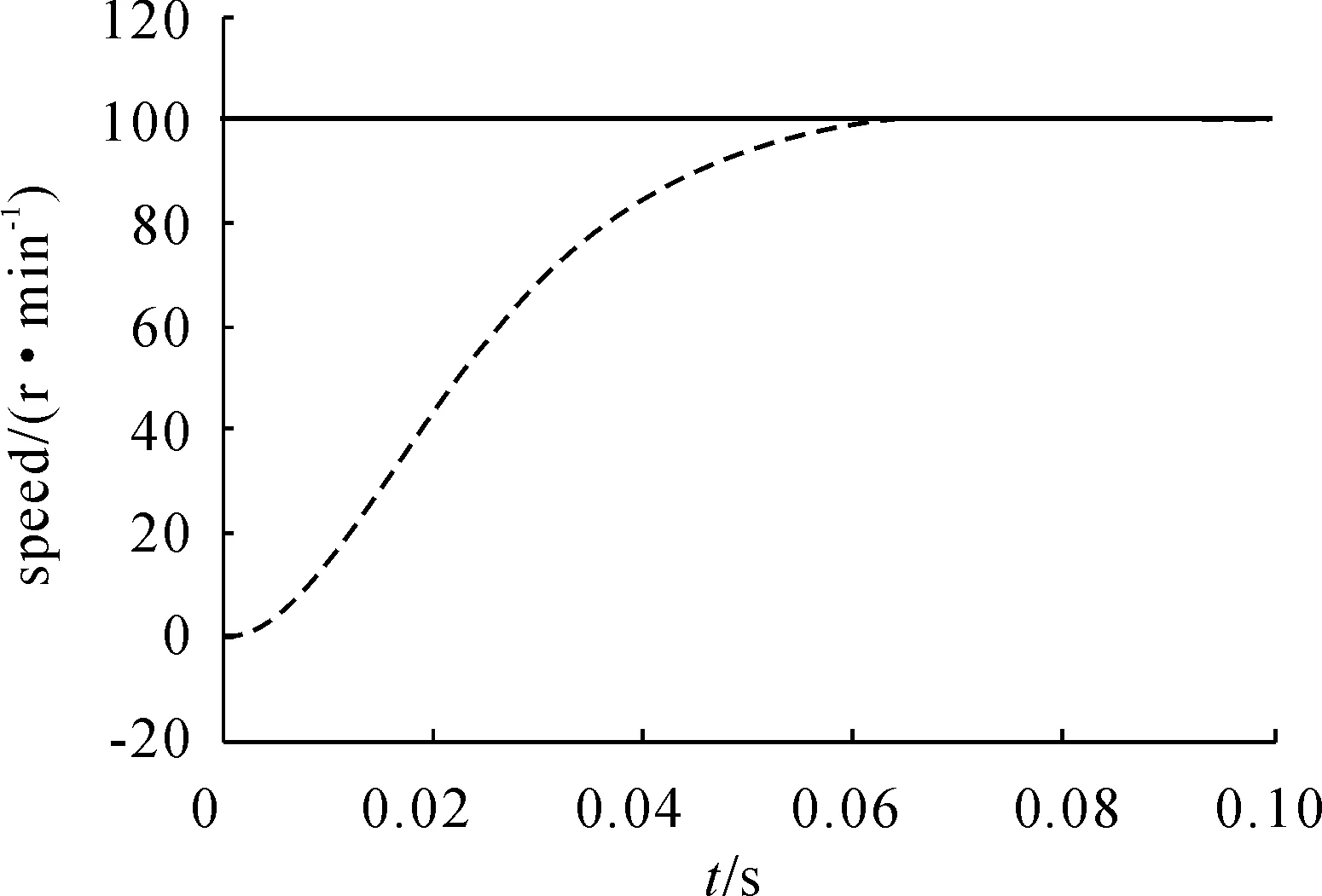
图6 速度响应曲线

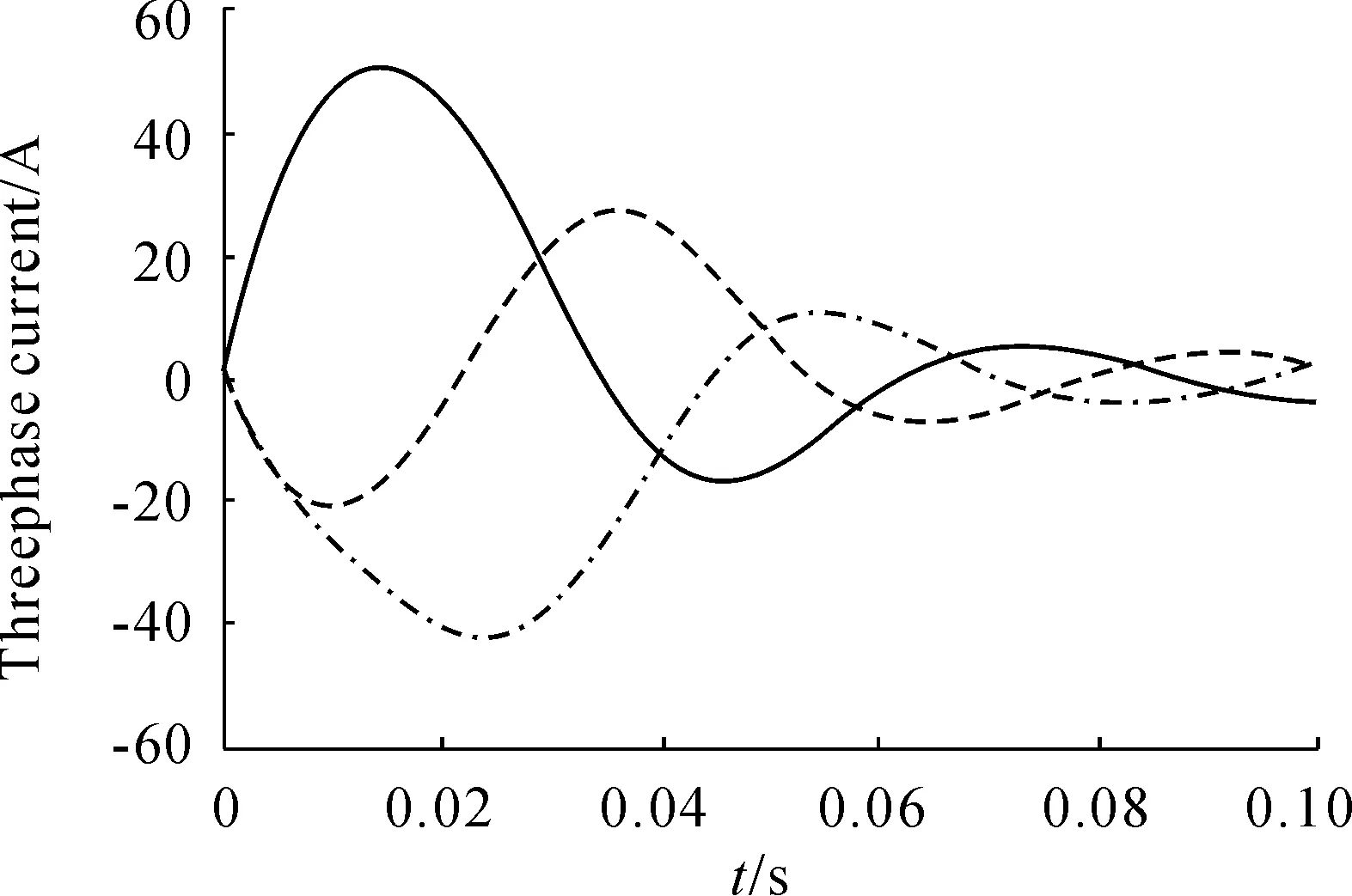
图7 三相电流响应曲线

图8 转矩响应曲线

由图6～8可见：指数趋近律滑模变结构控制下的转速响应波形无抖动和超调，在0.065 s时跟踪上给定转速；三相电流波形基本呈正弦波，几乎无畸变；转矩波形在下降段平滑地稳定为100 N·m，几乎无跳变现象。

在t=0.08 s时突加负载转矩TL=300 N·m，其他参数不变，在Simulink下仿真出如图(9)、(10)所示的转矩响应曲线，分别是速度环在PI控制下和在指数律滑模变结构控制下的转矩响应波形。

图9 突加负载后转矩响应曲线

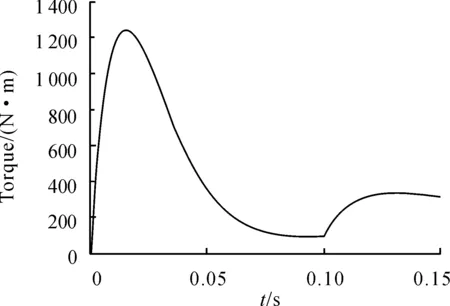
图10 滑模控制下突加负载后转矩响应曲线

通过对以上波形的对比不难发现：在t=0.08 s突加负载转矩TL=300 N·m后，传统PI控制下的转矩波形出现严重的波动与跳变现象；而在指数趋近律滑模变结构控制下，转矩波形能很平滑地跟踪到TL=300 N·m，几乎无波动。

4 结束语

本文利用指数趋近律的滑模控制方案设计了调速系统的速度环控制器，并在理论上分析了其稳定性和可行性。然后，基于Matlab仿真平台搭建了整个调速系统的模型(共2个仿真系统：一个是速度环在PI控制下的仿真系统，另一个是速度环在滑模变结构控制下的仿真系统)，调试参数后分别进行仿真，得到了各自仿真系统的转速、三相电流和转矩响应波形。通过比较，验证了将指数趋近律的滑模控制方案应用于矢量控制的永磁同步电机调速系统不仅可行，而且能提高系统的动静态性能。将滑模变结构控制策略应用于调速系统的速度环，可以实现快速、无超调的转速跟踪，而且对外界参数扰动不敏感，具有很好的自适应性。同时，滑模控制器设计算法简单，易于软件实现。

[1] Ge Baoming，Zhao Nan．DSP-based discrete—time reaching law control of switched reluctance motor[C]//Power Electronics and Motion Control Conference.[S.l.]:[s.n.]，2006：1-5.

[2] 韩广兵,苏浩,余丽莉,等.纳米复合永磁材料中软硬磁性相间交换耦合作用的表征[J].功能材料,2013(20)：2990-2995.

[3] 方斯琛，周波，黄佳佳，等.滑模控制永磁同步电动机调速系统[J].电工技术学报，2008,23(8)：29-35.

[4] 童克文，张兴，张昱，等.基于新型趋近律的永磁同步电动机滑模变结构控制[J].中国电机工程学报，2008，28(21):102-106.

[5] 陈荣.永磁同步电机控制系统[M].北京：中国水利水电出版社，2009.

[6] 汪海波，周波，方斯琛.永磁同步电机调速系统的趋近律滑模控制[J].微电机，2009，42(10)：44-48.

[7] Edward Y Y Ho,Paresh C sen.Control Dynamics of Speed Drive System Using Sliding Mode Controllers With Integral Compensation[J].IEEE 1991， 27：883-892.

[8] 喻林，刘彦呈，林安平，等.基于滑模变结构控制的PMSM矢量控制的研究[J].电气开关，2008,23(4)：23-26.

[9] 王芙蓉．PMSM伺服系统滑模变结构控制研究[D]．武汉：武汉理工大学，2006，24-47.

[10]盛严，王超，陈建斌，等.结构滑模控制的一种指数趋近律方法[J].噪声与振动控制，2002，4(31)：31-34.

[11]Liu Jun，Wu Pusheng，Bai Huayu，et al．Application of fuzzy control in direct torque control of permanent magnet synchronous motor[C]//Fifth World Congress on Intelligent Control and Automation.Hangzhou：[s.n.]，2004：4573-4576.

[12]李延波，杨立英，王汝凉.分布时滞不确定广义系统的滑模控制[J].西南大学学报:自然科学版,2013(5):56-60.

[13]夏天,陈龙,黄晨,等.EPS模糊滑模变结构控制仿真及试验研究[J].重庆理工大学学报:自然科学版，2014(3)：17-21.

[14]席雷平,陈自力,齐晓慧.具有抖振抑制特性的机械臂快速滑模变结构控制[J].电机与控制学报,2012(7):97-102.

[15]王金鹏,吴向东,张兵,等.滑模控制在变载荷高性能系统中的应用[J].重庆理工大学学报:自然科学版，2014(3)：53-59.

[16]周永勤,王旭东,张玉光,等.开关磁阻电机模糊滑模观测器间接位置检测[J].电机与控制学报,2013(6):57-63.

[17]武俊峰,李月.滑模变结构方法在两轮自平衡机器人上的应用[J].哈尔滨理工大学学报,2013(2):95-100.

[18]方一鸣,于晓,牛犇,等.永磁同步电机的自适应模糊终端滑模速度控制[J].中南大学学报:：自然科学版，2013(12)：4855-4860.

[19]高为炳.变结构控制理论基础[M]．北京：中国科学技术出版社，1990.

[20]张相庭，王志培，黄本才.结构振动力学[M].上海：同济大学出版社，2000.

(责任编辑 杨黎丽)

PMSM Sliding Mode Control Based on Reaching Law

ZHANG Hong-da, JIA Gui-xi, GUO Jin-bo, YANG Ting

(Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin 300072, China)

The traditional speed loop of the AC servo system mainly using PI control method. Even the control structure has many advantages such as simple control structure and high reliability, and it makes the system vulnerable to the volatile motor parameters and load disturbances. Sliding mode control can successfully overcome the above-mentioned defects of PI control method. By changing the system’s structure constantly, sliding mode control makes the system insensitive to the load disturbances and changeable motor parameters, thus enhancing the robustness of the system. Therefore, it is expected to be widely used in high-performance servo systems. Theid=0 control method was adopted in this paper and a reaching law sliding mode controller was designed on this basis. Then the PI control method frequently applied in speed loop was replaced by this controller. The feasibility and superiority were tested through simulation results in the end.

permanent magnet synchronous motor; vector control; sliding mode control; reaching law; servo system

2014-12-03 基金项目：国家自然科学基金资助项目(61172014)；国际科技合作与交流专项项目(2013DFA11040)

张宏达(1989—)，男，天津人，硕士研究生，主要从事电力电子与电力传动方面研究。

张宏达，贾贵玺，郭锦波， 等.永磁同步电机的趋近律滑模控制[J].重庆理工大学学报：自然科学版，2015(3):89-94.

format：ZHANG Hong-da, JIA Gui-xi, GUO Jin-bo, et al.PMSM Sliding Mode Control Based on Reaching Law[J].Journal of Chongqing University of Technology:Natural Science,2015(3):89-94.

10.3969/j.issn.1674-8425(z).2015.03.017

TP273

A

1674-8425(2015)03-0089-06