基于数字图像的碎纸复原模型与算法——2013年全国大学生数学建模B题碎纸片的拼接复原问题

刘 铁

(安康学院 数学与统计系 数学与应用数学研究所，陕西 安康 725000)



基于数字图像的碎纸复原模型与算法
——2013年全国大学生数学建模B题碎纸片的拼接复原问题

刘 铁

(安康学院 数学与统计系 数学与应用数学研究所，陕西 安康 725000)

传统的拼接复原工作需由人工完成，准确率较高，但效率很低。针对该问题，借助数字图像处理技术，建立了关于图片匹配度函数的优化模型，依据穷举思想设计了求解算法，可大幅提高复原效率，但在处理复杂问题时，准确性有所下降，需要一定的人工介入。通过对复原后图片的验证结果可知，碎纸片复原拼接模型具有可行性。

数字图像;碎纸复原;匹配度

数字图像的拼接复原技术在生产、生活中有着广泛的应用[1-12]。碎纸片的拼接复原问题有重要的实际研究价值。传统上，拼接复原工作需由人工完成，准确率较高，但效率很低。特别是当碎片数量巨大时，人工拼接很难在短时间内完成。随着计算机技术的发展，人们试图开发碎纸片的自动拼接技术以提高效率。 本文针对2013年全国大学生数学建模竞赛中碎纸片的拼接复原问题进行研究[13]。碎纸片拼接复原问题包括以下内容：

1) 对于给定的来自同一页文字文件(单面打印)的碎纸机破碎纸片(仅纵切为19条)，建立碎纸片拼接复原模型和算法，并针对题目中附件1(中文纵切图片)、附件2(英文纵切图片)给出的中、英文各一页文件的碎片数据进行拼接复原；

2) 对于碎纸机既纵切又横切的情形(切为11×19，共209块)，设计碎纸片拼接复原模型和算法，并针对题目中附件3(中文纵、横切图片)、附件4(英文纵、横切图片)给出的中、英文各一页文件的碎片数据进行拼接复原；

3) 解决双面打印文件的碎纸片拼接复原问题，并对题目中附件5(英文双面纵、横切图片)给出的一页英文印刷文字双面打印文件的碎片数据进行拼接。

1 匹配度定义

首先，借助Matlab图像处理函数imread读取题中BMP图片为灰度图矩阵。其次，再利用函数im2bw将图片转化为二值图矩阵，0和1分别表示黑色与白色[14]。对矩阵进行两两比对,以i矩阵最右边一列与j矩阵最左边一列进行配对,定义匹配度函数：

其中：ni为配对成功的行数；n为矩阵总行数。如此形成匹配度矩阵Dm×m,其中m为图片张数。显然该矩阵为非对称矩阵。

2 问题1的模型与算法

以两条碎片之间的匹配度取倒数作为距离,将问题转化为TSP问题[15]。 需要说明的是，为了避免出现分母为零的情形,在取倒数前应统一加上机器零——eps。设

辅助变量ui可以反映图片连接的前后次序，取值越小越先连接。 采用破圈法[16]建立如下优化模型：

编制LINGO程序求解模型，得到最优解。

为提高求解效率，可先提取各矩阵左侧页边空白宽度信息，即编程查找矩阵左侧分量均为1的列向量列数，根据左侧空白来确定最左边的图片，将它作为起点求一个最佳巡回路线。 附件1中中文页仅有的008图左侧页边空白列数非零，即为起点，其最优结果见表1。附件2中英文页的003图为起点，其最优结果见表2。

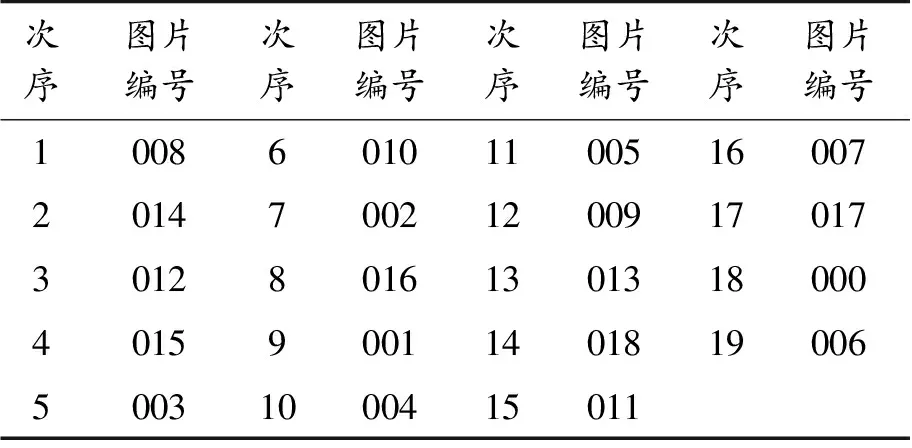
表1 附件1中文复位次序表

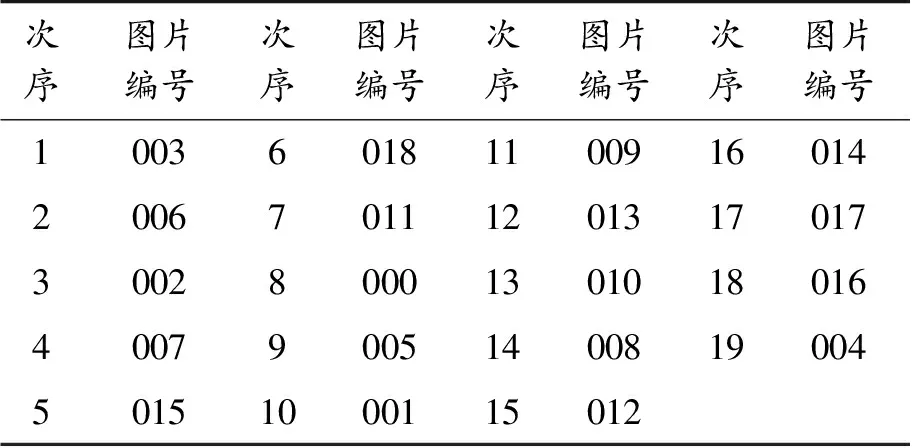
表2 附件2英文复位次序表

3 问题2的模型与算法

问题1仅有纵切，每一条纸片的长度较大，使得可提取的纸边信息充足，不需要人工干预，复原率可以接近或达到100%。 但问题2不仅对纸张进行纵切还进行横切，将一张完整的纸张切割为11×19张小纸片。 如果直接应用问题1中的方法，一方面图片块数大幅增加，TSP问题无法处理209个点的问题；另一方面，每幅图边缘信息量也大幅度减少，极易出现错配， 需要适当的人工干预。

利用Matlab软件编程提取每张图片的上下页边空白宽度信息，即查找矩阵上下各分量均为1的行向量行数记为Ui和Li，分别利用上边空白宽度数据Ui和下边空白宽度数据Li做聚类分析。对于类中数据多于19的组取交集,不足19的类就近取类的并集。 也可加入人工甄别,初步获得各行的大致分类。在得到行聚类结果后，利用类似于问题1中的方法完成每行碎片的排序工作。期间会出现不少错配情况，此时将配对正确的片段记下，然后除去它们，再将剩余的图片用TSP法寻优,直到将此行排定,再排其他行。 最后，对排序后的行作纵向排序。方法与问题1中类似，只不过先根据上边空白宽度信息确定第1行,以i行矩阵的末行向量与j行矩阵的首行向量做比对,匹配度公式为

此时的ni为配对成功的列数,n为矩阵总列数。之后的步骤与问题1相同。附件3中的中文页结果见表3。

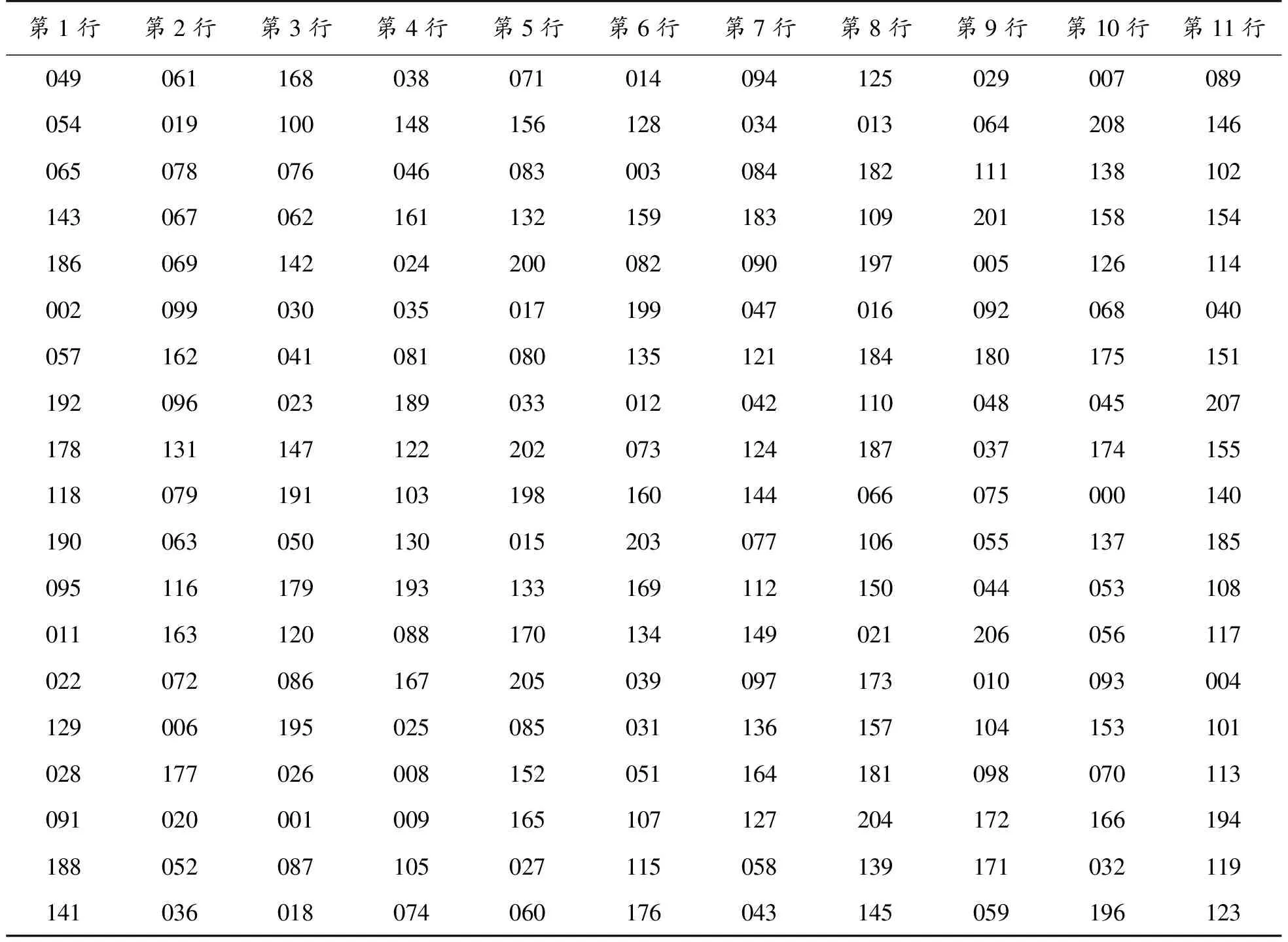
表3 附件3中文复位次序表

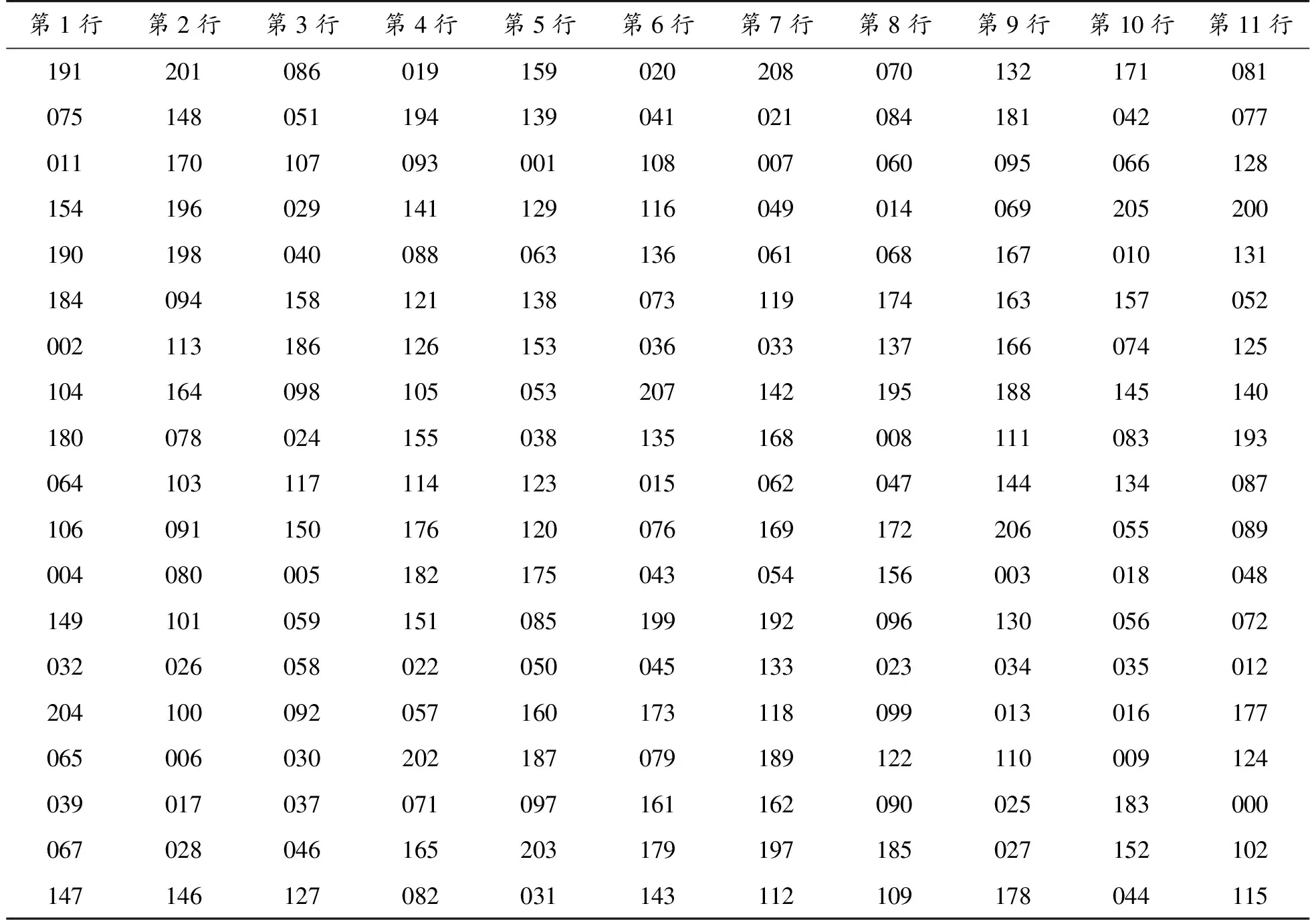
如图1所示,相比中文，英文的情形要复杂得多。英文中除了存在一些“y”，“b”之类的字母与行聚类强相关以外，还有“e”和“a”之类无法判定所属行的干扰字母，妨碍对同行信息的判定，聚类效果较差，需要大量的人工判定。另外，需要把这些无法判定所属行的图片与最容易判定的行(不足19片)一起做行排序。将使用的图片剔除后，将剩余图片与其他行一起再排序，以逐步减少干扰图片的数量。其余方法和过程与中文类似。 附件4中英文页求解结果见表4。

图1 英文的复杂性示意图

第1行第2行第3行第4行第5行第6行第7行第8行第9行第10行第11行191201086019159020208070132171081075148051194139041021084181042077011170107093001108007060095066128154196029141129116049014069205200190198040088063136061068167010131184094158121138073119174163157052002113186126153036033137166074125104164098105053207142195188145140180078024155038135168008111083193064103117114123015062047144134087106091150176120076169172206055089004080005182175043054156003018048149101059151085199192096130056072032026058022050045133023034035012204100092057160173118099013016177065006030202187079189122110009124039017037071097161162090025183000067028046165203179197185027152102147146127082031143112109178044115

4 问题3的模型与算法

问题3是问题2的继续，基本解决方法与问题2的方法相同，不同的是，这里需要充分利用双面文本的特征信息。 一般认为，双面信息使得任务量不止增大一倍,干扰信息也更多。 以纸片i与j为例，匹配方式可能为：

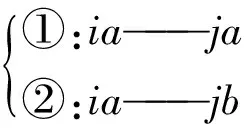
本不对应的两张碎纸片两面的拼接复原情况均好的情况只可能是个别案例，所以可将碎纸片两面边缘匹配度之和作为评判两张图片是否匹配的标准,建立边缘匹配度之和矩阵D′。为进一步提升复原率,通过提取每张图片左右边缘空白宽度信息发现，编号为i的碎纸片a面右端(或左端)与b面左端(或右端)边缘全是白色的图片一共有22张。考虑到所有的碎纸片应被拼接为11行，而左右两端乘以2就是22，所以136，005，143，083，090，013，035，172，105，009，054，078，089，186，199，088，114，146，165，003，023，099这22张碎纸片应是原文件纸张的两端。 为了方便，可以选择这22张碎纸片作为开端匹配对应的纸片。下面的过程与问题2类似， 结果见表5、6。

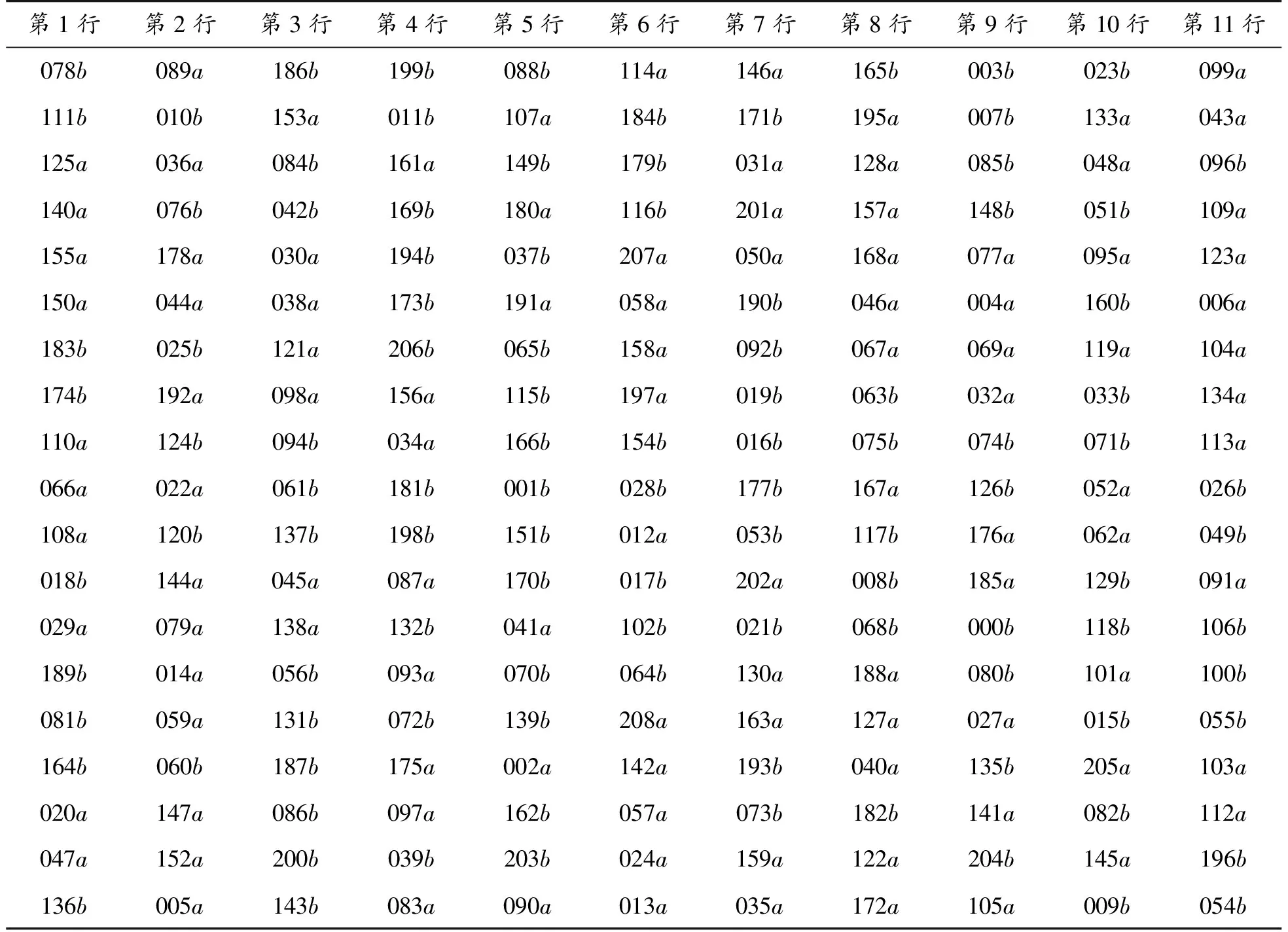
表5 附件5双面英文正面的复位次序表

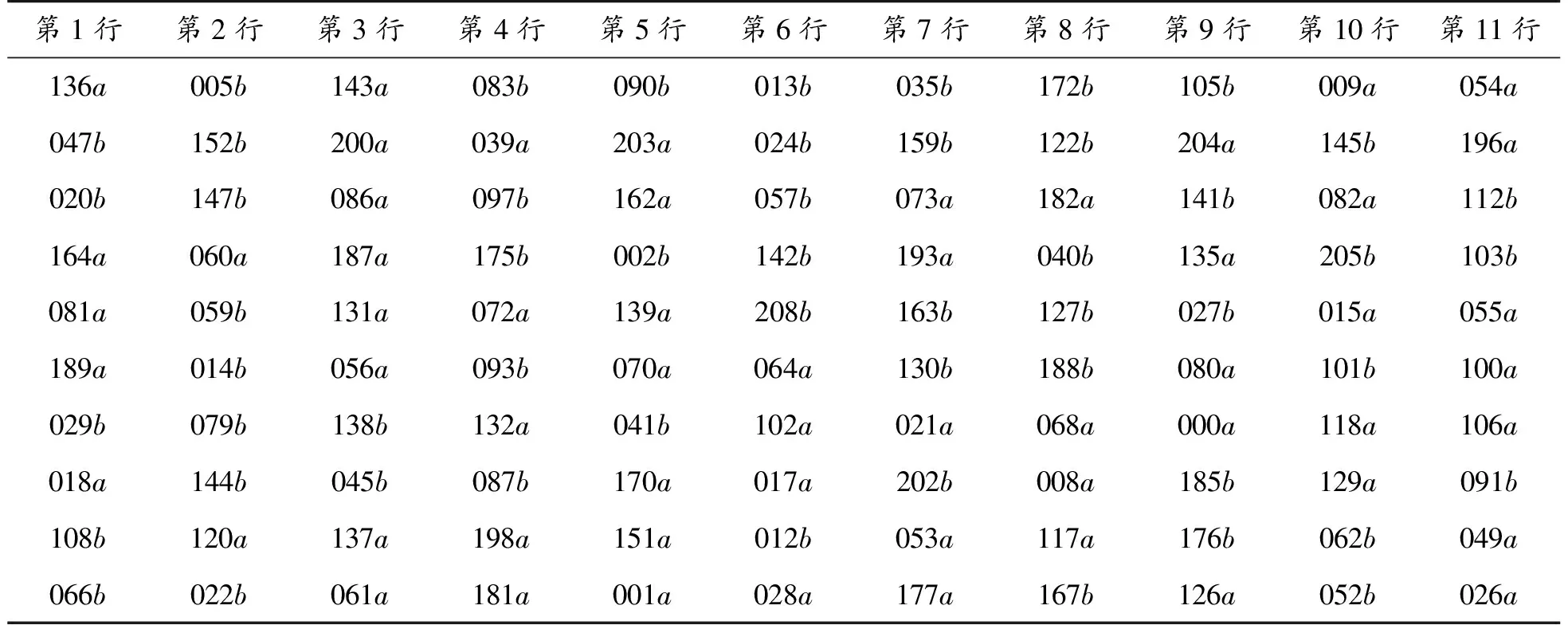
表6 附件5双面英文反面的复位次序表

续表

第1行第2行第3行第4行第5行第6行第7行第8行第9行第10行第11行110b124a094a034b166a154a016a075a074a071a113b174a192b098b156b115a197b019a063a032b033a134b183a025a121b206a065a158b092a067b069b119b104b150b044b038b173a191b058b190a046b004b160a006b155b178b030b194a037a207b050b168b077b095b123b140b076a042a169a180b116a201b157b148a051a109b125b036b084a161b149a179a031b128b085a048b096a111a010a153b011a107b184a171a195b007a133b043b078a089b186a199a088a114b146b165a003a023a099b

5 结束语

通过对复原后图片的验证结果发现，本文中的碎纸片复原拼接模型对于本题有很高的可行性。 对于中、英文两种情况，按照从问题1到问题3、中文到英文的顺序依次改进模型与算法，发现中文需要人工干预较少、英文需要人工干预较多的规律，说明不同语言有各自的特性。

对于计算机错误匹配的结果，在问题2与问题3中给出了详细的人工干预的时机与方法，通过检验结果说明人工干预是必需的。

本文模型适用于打印文件之类的平面规则碎片的拼接复原问题,且不涉及碎片残缺不全的情形。对于不规则的立体残片，例如考古挖掘出的不规则文物或者钞票残片等，还需要开发更好的改进模型来进行研究。

[1] 戚文静,赵敬.基于数字全息的图像置乱的研究[J].山东大学学报：理学版,2005,40(5):93-96.

[2] 罗智中.基于文字特征的文档碎纸片半自动拼接[J].计算机工程与应用，2012,37(6):207-210.

[3] 潘斌，郭小明，陈明明，等.规则切割碎纸片的复原[J].辽宁石油化工大学学报,2014,34(5):70-73.

[4] 陈黎黎 ,国红军.基于文档内容的碎纸拼接技术[J].衡水学院学报,2014,16(4):34-37.

[5] 王威娜,史彦丽.无重叠的文档碎片拼接方法[J].吉 林化工学院学报,2014,31(3):85-87.

[6] 林川，张学新.一种纵切碎纸片拼接算法[J].湖北工程学院学报,2014,34(3):37-40.

[7] 樊庆文,王小龙,侯力,等.基于等距序列图像的快速拼接技术[J].四川大学学报:工程科学版,2005,37(1):139-142.

[8] 王书民,张爱武,崔营营,等.基于无人飞艇数字摄影测量系统及航拍序列图像拼接[J].测绘科学,2010,35(4):81-83.

[9] 郭丙轩,王文进,刘 波,等.一种基于网格的数码相机数字化图像纠正拼接算法[J].测绘科学,2007,32(6):143-145.

[10]潘荣江,孟祥旭,屠长河.一种基于LCS 的物体碎片自动拼接方法[J].计算机学报,2005,28(3):350-156.

[11]王晨，杜彦，杜建洪.基于块缺失图像修复技术的研究与应用[J].计算机工程,2006,32(11):206-208.

[12]牛刚.基于特征像素统计的图像相关匹配算法[EB/OL].[2013-09-13].http://www.docin.com/p-87674921.html.

[13]CVMCM.2013年高教社杯全国大学生数学建模竞赛赛题[EB/OL].[2014-09-25].http://www.mcm.edu.cn/problem/2013/2013.html.

[14]章毓晋.图像处理[M].北京:清华大学出版社，2012:21-43.

[15]司守奎、孙玺菁.数学建模算法与应用[M].北京：国防工业出版社，2011:109-152.

[16]袁新生,邵大宏,郁时炼.LINGO和Excel在数学建模中的应用[M].北京：科学出版社,2007:55-105.

(责任编辑 杨黎丽)

Mathematical Model and Algorithm Design on Reconstruction of Shredded Document Based on Digital Image：National College Students’ Mathematical Modeling

LIU Tie

(Institute of Mathematics and Applied Mathematics, Department of Mathematics and Statistics, Ankang University, Ankang 725000, China)

Traditionally, restoration works need to be done by hand, which has high accurately, but is inefficiently. With the aid of digital image processing technology, optimization model on matched-degree of image was established, and algorithm based on exhaustive thought was proposed. It can significantly improve the recovery efficiency, but when dealing with complex problems, the accuracy of solutions may be severely degraded, and artificial intervention is required.

digital Image; reconstruction of shredded document; matched-degree

2014-10-23 基金项目：国家自然科学基金资助项目(61152003)

刘铁(1978—)，男，黑龙江齐齐哈尔人，硕士，讲师，主要从事数学建模、微分方程、优化理论研究。

基于数字图像的碎纸复原模型与算法 ——2013年全国大学生数学建模B题碎纸片的拼接复原问题[J].重庆理工大学学报：自然科学版，2015(3):83-88.

format：LIU Tie.Mathematical Model and Algorithm Design on Reconstruction of Shredded Document Based on Digital Image： Reconstruction of Shredded Papers of Section B in 2013National College Students’ Mathematical Modeling [J].Journal of Chongqing University of Technology:Natural Science,2015(3):83-88.

10.3969/j.issn.1674-8425(z).2015.03.016

TP393; O221

A

1674-8425(2015)03-0083-06