基于交互式遗传算法的群体评价模型——以水利人才为例

马瑞敏,卞艺杰,吴 慧

(河海大学 商学院，南京 211100)



基于交互式遗传算法的群体评价模型
——以水利人才为例

马瑞敏,卞艺杰,吴 慧

(河海大学 商学院，南京 211100)

针对水利人才评价的复杂决策问题，提出了一种基于交互式遗传算法的群体评价模型。以交互式遗传算法中适应度值为接口，实现了群体评价方法与交互式遗传算法的结合，通过人工智能技术把定性指标定量化，解决了水利人才评价这类复杂决策问题的优化目标非定量化的问题。在Matlab环境下建立仿真模型，并将其用于水利人才的评价。实验结果表明：该模型是可行和有效的，为这类复杂、模糊的决策问题提供了一种解决方法。

交互式遗传算法；群体评价；层次分析法；水利人才

人们在日常生活中遇到的复杂决策问题大多是开放的复杂巨系统的问题，如国民经济发展预测、军事对阵、环境保护区域规划等。这类复杂性问题的结构都是极其不良的，包括3个方面：初始状态不明确、目标状态不明确和操作不明确[1]。本文研究的水利人才的评价问题就是一类复杂的决策问题。通过分析发现，可以通过各种定性指标和定量指标来反映人才的能力和各种技术水平。这种人才评价问题具有目标函数不明确、结构不清晰、求解空间大、无明确的求解方案的特点，是典型的隐型目标决策问题。如何在决策过程中以较高的效率获得群体意见共识成为极大的挑战。由于传统的评价方法存在可操作性及群体共识的最大化方面不理想的缺点，因此本文构建基于交互式遗传算法的群体评价模型，选用层次分析法得到个体的适应度值来代替难以或无法显式表示的适应度函数，群体论证具有准确度高、平均效益大的特点；另一方面，交互式遗传算法是解决复杂的大型决策问题的有效方法，它进行全局优化自适应搜索，在决策的过程中不断进化和完善。因此，群体论证和交互式遗传算法相结合的方法是解决这类复杂决策问题的有效方法。

1 面向水利人才的群体评价方法

在生产和社会实践中，经常遇到诸如产品评优、工农业产品定级、设计方案评选、成果评价之类的评价活动。这时常由多个评价者构成评价组，集中各评价者意见，用其作为群体的意见，这种集合评价者意见的方法及将其用于评价的行为称为群体评价[2]。评价本身带有很强的主观性，各个决策者的主观行为(如经验、判断、观察力、决策风格等)对各阶段的评估效果都有很大的影响。因此，考虑到个别专家的评价具有片面性，为了克服这一缺点，人们在进行重要决策或评价时，往往需要多个专家的意见，以得到更为科学的结果。

1.1 评价对象

本文以水利人才为对象进行研究。水资源是基础性的自然资源和战略性的经济资源，是生态与环境的重要控制因素。水利工作与民生密切相关，水利事业事关人民生存与发展。党的十七大把水利工作摆上重要位置，提出了更高要求。按照全面建设小康社会的要求，到2020年，要基本建成重点流域和区域综合防洪减灾体系、城乡水资源合理配置和高效利用体系、水环境保护和河湖生态健康保障体系、较为完善的管理和运行保障体系等四大体系[3]。对于水利工作的高要求和水利体系的建设而言，水利人才尤为重要，优秀的水利人才为水利事业的发展提供了专业的保障，为水利体系的建设提供了良好的支撑。但是，目前水利人才队伍的现状还不能完全适应水利事业发展的需要。主要表现在：水利系统人才总量不足和高层次人才缺乏的问题仍未得到根本解决，高技能、复合型、创新型人才紧缺，人才结构和分布不合理的问题依然存在[3]。因此，如何选拔优秀的水利人才，对水利事业的发展至关重要。

1.2 面向水利人才的群体评价方法优选

随着群体评价的研究越来越受到人们的关注，出现了各种群体评价方法，现有评价方法有专家会议法、德尔菲法、加权求和法、模糊综合评价法、层次分析法及其扩展方法等。现有的群体评价方法有很多，因此需要选择一个适合水利人才群体评价的方法。对以上5种群体评价方法进行的对比见表1。

表1 群体评价方法对比

通过对比可知：专家会议法最大的缺点是人际冲突，即成员易屈服于权威或大多数人的意见，易受劝说性意见的影响。德尔菲法虽然避免了这一缺点，但是德尔菲法的决策速度较慢，时间成本高，而且不适用于结构模糊复杂的问题。加权求和法看重不同专家在评价中的地位对评价结果的影响，但没有考虑专家之间评价一致性的影响，不能保证评价结果的合理性。模糊综合评价法和层次分析法都考虑了影响决策问题的各种因素的作用，但对于多层次、多目标的问题，层次分析法能确定各层次的各个因素对决策问题的影响，相比模糊综合评价方法的使用范围更广。

通过以上对比可知，层次分析法较适合于水利人才的评价。首先，水利人才评价这一问题难以量化，存在多个定性指标，层次分析法将影响水利人才评价的多个因素分解为多个目标或准则，形成一个多层次的分析模型，可有效地将定性指标定量化；其次，层次分析法的决策速度较快，可以避免群体专家因决策时间过长而产生疲劳；再次，群体专家各自对水利人才进行层次分析，然后根据各个专家的权重进行加权平均，有效地减少了专家之间的冲突。因此，层次分析法可作为水利人才评价的一个优选评价方法。

2 基于交互式遗传算法的群体评价模型

交互式遗传算法(interactive genetic algorithm,IGA)是对遗传算法改进后的算法，它基于人的主观评价，是人机交互与遗传算法相结合的产物，将人的主观评价与计算机技术相结合，利用人的主观评价得到进化个体适应值，用来代替难以或无法显示表示的适应度函数。它是解决定性指标优化问题的有效方法，是人的智能评价与遗传算法的优化能力相结合的产物，体现了个体决策者对问题带有主观性和不确定性评价的决策过程。

基于交互式遗传算法的群体评价模型利用群体评价的方法得到个体的适应度值，进行选择、交叉和变异的遗传操作，不断地进行迭代进化，直到达到终止条件为止。其中层次分析法模型有效地将定性指标定量化，充分考虑了各个指标的影响程度，合理计算出每个个体的综合评分，并作为每个个体的适应度值，以适应度值为接口将层次分析法模型嵌入到交互式遗传算法模型中，为复杂的决策问题提供了一种解决方法。

2.1 构建总模型

根据之前确定的面向水利人才的群体评价方法——层次分析法，得到进化个体的适应度值来代替传统的遗传算法的适应度函数，并以此为接口，将层次分析法的群体评价方法与交互式遗传算法相结合，得到基于交互式遗传算法的群体评价模型，如图1所示。

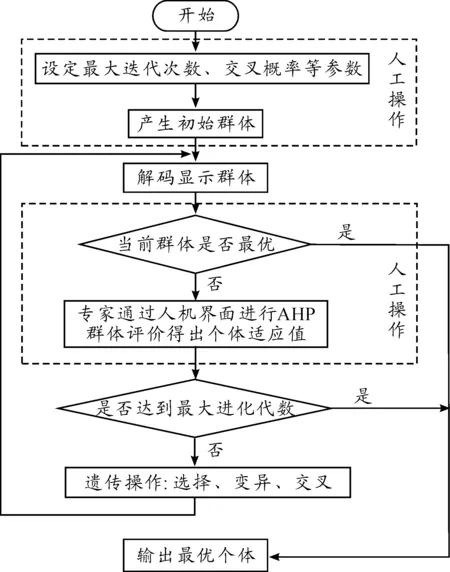
图1 基于交互式遗传算法的群体评价模型

步骤流程如下：

Step 1 通过人机界面，由专家设定群体大小N、遗传因子概率及终止代数T等参数，并产生N个个体作为初始种群；

Step 2 解码，将进化个体的表现型提交给参与评价的专家群体；

Step 3 由专家群体判断种群中的个体是否达到最优，若是，则输出最优个体；否则，转到Step 4；

Step 4 专家通过人机界面进行群体评价得出个体适应值，进入层次分析子模型；

Step 5 判断群体进化是否达到最大进化代数，若是，则输出最优个体；否则，转到Step 6；

Step 6 系统进行遗传操作，包括选择、交叉、变异，得到新一代群体，转到Step 2。

2.2 模型说明

1) 确定各种参数或约束条件

设定编码串长度l、群体大小N、交叉概率pc、变异概率pm、终止代数T等参数。

群体大小N：表示群体中包含的个体的总量，当N取值较小时，降低了群体的多样性，有可能导致算法出现早熟现象，但是可提高算法的运算速度；反之，算法运算速度会降低。

交叉概率pc：遗传算法主要通过交叉操作产生新个体，因此pc取值应较大。但是如果pc取值过大，会破坏群体现有的优良结构，反而不利于群体进化；反之，若取值过小，产生新个体的速度会较慢。一般建议的取值范围是0.4～0.99。

变异概率pm：遗传算法也可通过变异产生新个体，但是如果变异概率取值较大，也容易破坏群体的优良结构；反之，若取值过小，则变异操作产生新个体的能力和抑制早熟现象的能力就会较差。一般建议的取值范围是0.000 1～0.1。

终止代数T：表示遗传算法运行到第T代停止进化，并将当前群体中的最佳个体作为最优解输出。一般建议的取值范围是100～1 000。

2) 确定表示可行解的染色体的编码方法

根据层次分析模型，指标层中的各项指标对应于遗传算法中个体的某个基因，一个个体对应于遗传算法中的一个染色体，其编码可选择遗传算法最常用的二进制编码。二进制编码操作简单易行，交叉、变异等遗传操作便于实现。通过解码二进制，将个体通过人机界面呈现给参与评价的专家。

3) 确定个体适应度的评价方法

利用交互式遗传算法进行水利人才群体评价时，专家对每一个个体都有自己的主观判断，据此专家通过层次分析法对每一个个体给出评价值，系统根据各个专家的打分，求取每一个个体的综合得分作为该个体的适应度值Fi。

4) 设计遗传算子

确定选择运算、交叉运算、变异运算等遗传算子的具体操作方法。

选择：选择操作以个体适应度值为基础对个体进行优胜劣汰的操作，是遗传算法中实现群体优良基因传播的基本方式。遗传算法中最常用的选择方法是比例选择，其基本思想是个体被选中的概率与其适应度大小成正比。设群体规模大小为N，第i个个体的适应度为Fi，则个体i被选中的概率pi为

由上式可见：个体适应度值越高，被选中的概率越大；反之，个体被选中的概率就越小。被选中的个体进入繁殖池，并从原群体中去除，直到繁殖池中群体规模达到N为止。

交叉：交叉运算是指对两两配对的染色体相互交换其部分基因，从而形成2个新的个体。本文采用最常用的交叉算子(即单点交叉算子)，将交叉点随机设置在个体编码串中，然后在该点交换已配对的两个个体的部分染色体，交叉概率为pc。

变异：是指通过将个体染色体编码串中的某些基因座上的基因值用其他等位基因来替换以产生新个体的方法。本文采用最简单的变异算子，即基本位变异算子，对二进制编码所表示的个体的某一基因座进行变异操作，若原有基因值为0，则变异操作将该基因值变为1；反之，若原有基因值为1，则变异操作将其变为0，变异概率为pm。

2.3 构建层次分析子模型

采用层次分析法，将影响水利人才评价的多个因素根据目标分解为多个目标或准则，进而分解为多个指标的若干层次，形成一个多层次的分析模型。

2.3.1 确立评价指标体系

人才评价指标体系根据其具体应用范围和评价目的不同，采用的构架也有所区别。指标体系一般分为3个层次：第一层是目标层，反映指标体系所追求的目标；第二层是准则层，反映评价的具体目标，是构造评价指标体系的依据；第三层是指标层，从不同方面反映评价的直接效果和间接效果[4]。本文对水利人才的评价指标体系采用这种结构：第一层目标层A是水利人才评价；第二层的准则层B主要包括学识水平、工作能力、工作经历3个方面；第三层指标层C对准则层划分详细的指标，见图2。

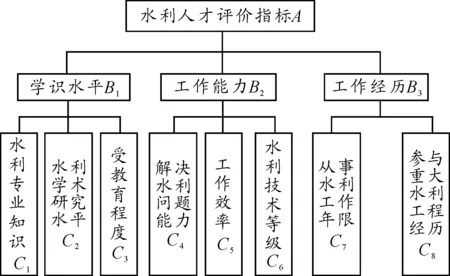
图2 水利人才评价指标体系

2.3.2 综合测评打分

按照图2的层次结构，应用表度法，通过专家的讨论，建立该评价体系的各个层次的比较判断矩阵。为了能科学地反映各个指标的相对重要性，在取得判断矩阵的权重向量后，需对其进行一致性检验，依据CR值判定判断矩阵是否通过一致性检验，若CR<0.1，具有满意的一致性，该判断矩阵可以用来做层次分析；若CR>0.1，则需要重新给出相对重要度评价，直到满足CR<0.1。综合各层次单排序的计算结果，可以得到指标层C中的各指标相对于总目标层A的权重，计算过程如下：Wj=Bi*Cj。其中，Wj是指标Cj对目标层的权重；Bi是准则层中Bi因素对目标层的权重；Cj是Bi对应的指标Cj对该准则层的权重。

3 实例仿真

3.1 实验设置及过程

3.1.1 实验设置

在Matlab环境下开发了一个仿真系统，参与群体评价的专家经过讨论确定水利人才的评价指标。对于这些评价指标，专家的定性评价按等级制，并通过指标层的指标编码群体中的个体。本系统采用二进制编码，编码及表现型如表2所示。

表2 二进制编码及表现型

如表2所示，每个指标的参数有4种选择，从高到低分别代表3分、2分、1分、0分，编码为2位，因此一个方案的个体编码为2×8=16位，系统产生的搜索空间为48=65 536。每种编码组合唯一确定一个个体，个体的编码结构如表3所示。

表3 个体的二进制编码结构

表3中：1表示水利专业知识；2表示水利学术研究水平；3表示受教育程度；4表示解决水利问题的能力；5表示工作效率；6表示水利技术等级；7表示从事水利工作年限；8表示参与重大水利工程经历。

假设此次群体评价由大学水利专家，水利局管理者以及水利基层工作者共同参与，3种评价者的权重设置如表4所示。

表4 评价者权重

假设群体评价的专家经过讨论确定最大进化代数T、种群规模N、交叉概率pc、变异概率pm等参数的设置，如表5所示。

表5 参数设置

3.1.2 实验过程

首先，进入参数设置窗口(如图3所示)，设置交叉概率pc、变异概率pm、种群规模N、最大进化代数T。系统默认值分别为pc=0.6，pm=0.001，N=8，T=15(可根据实际情况设置为100～1 000)。

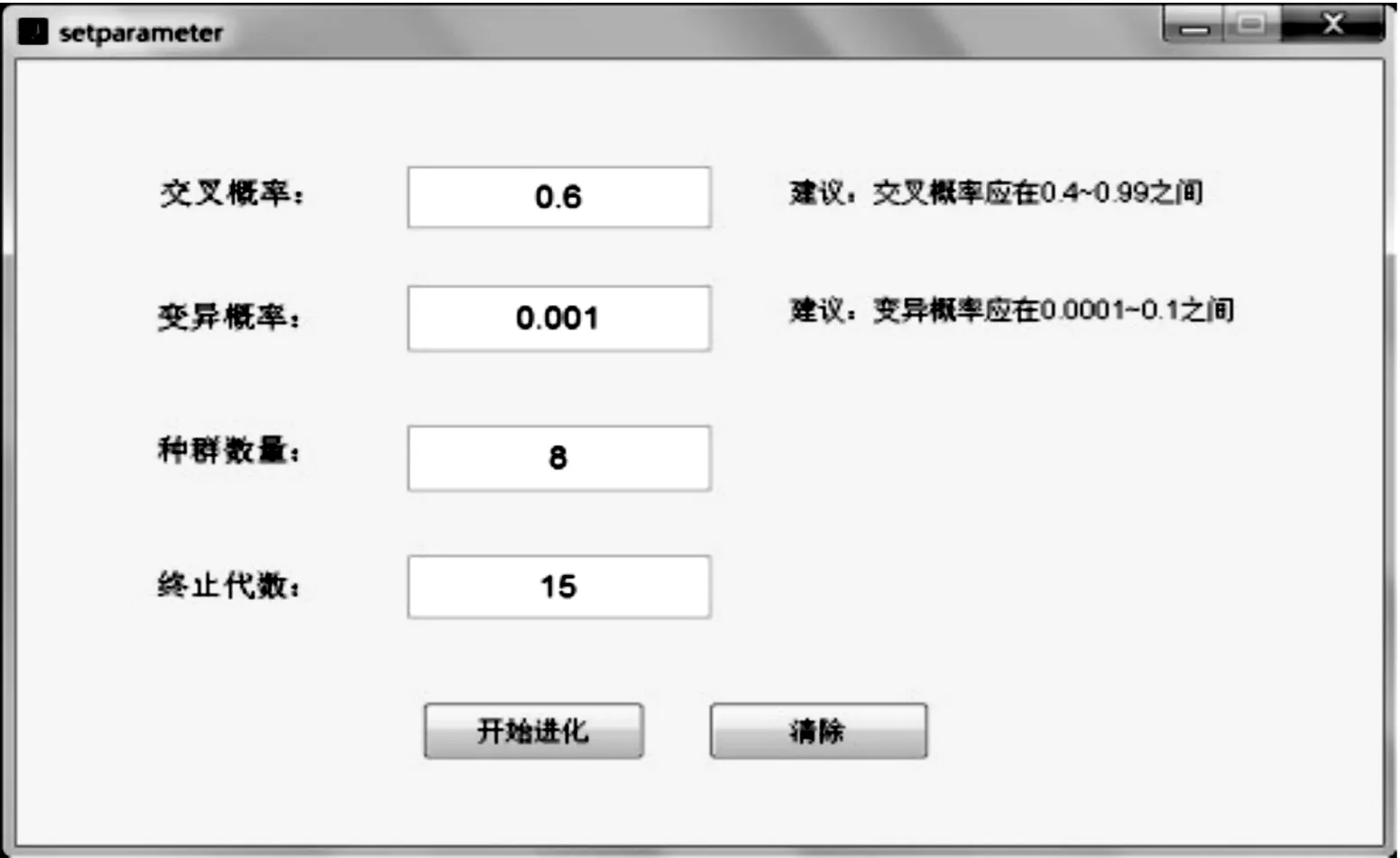
图3 参数设置

完成参数设置后，进入系统主界面(如图4)。首先，进行初始化操作，由系统自动生成初始化群体，个体基因型解码后转化为表现型在图形用户界面中显示出来。

图4 基于交互式遗传算法的群体评价模型主界面

然后，单击“判断矩阵”按钮，弹出判断矩阵设置窗口。此次群体评价的参与者为大学水利专家(如图5)，大学水利专家根据对话框显示的水利人才评价指标体系，完成判断矩阵，充分体现了人机交互功能。大学水利专家评价完成后，再分别由水利局管理者和水利基层工作者进行评价。三者组成的群体专家评价完成后，根据之前已确定的3类专家的权重，将评价结果加权平均，最终得到评价指标体系各层的判断矩阵。

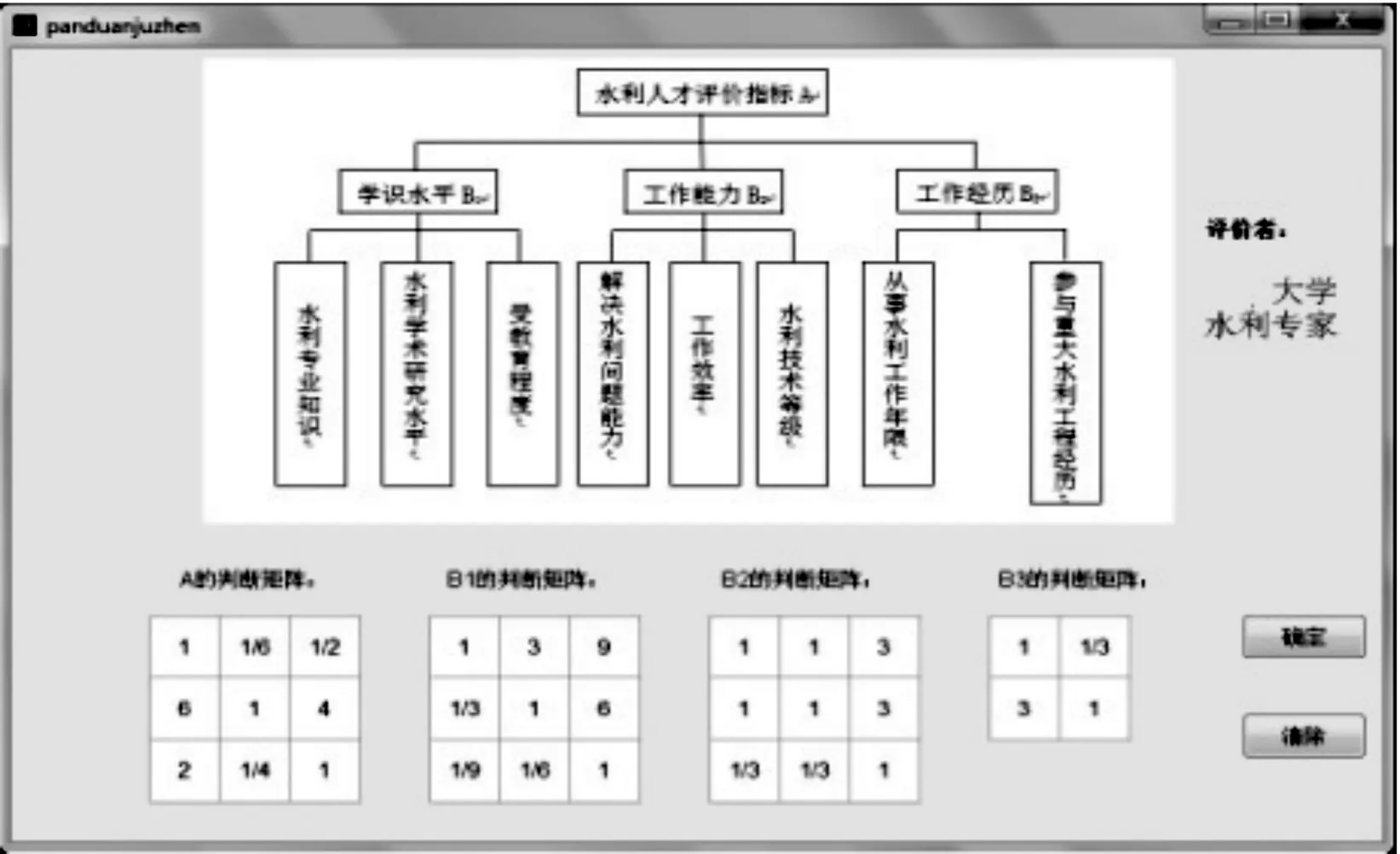
图5 大学水利专家参与评价

专家评价完成后，单击 “下一代”按钮，开始进化.。后台通过群体专家评价得到的判断矩阵计算个体的适应度值，进行选择、交叉、变异的遗传操作产生新一代的群体，系统解码后，将个体的表现型显示出来，如图6所示。进行迭代进化直到产生专家满意的个体，或是达到最大进化代数为止。

图6 进化产生新群体

最后输出此次进化过程中的最优个体，如图7所示。

图7 最优个体

3.2 实验结果分析

在此次进化过程中，不仅得到了最优个体，而且由大学水利专家、水利局管理者和水利基层工作者组成的群体专家评价后得到了水利评价体系中指标层各指标的权重，如表6所示。其中，解决水利问题的能力和工作效率所占比重最大，对评价的影响程度最大，参与水利工程的经历次之，水利技术等级第三。因此，对水利人才除了注重专业知识和技术的培养之外，教育工作者和水利工作单位还应为其提供更多的参与水利工程建设的机会，使其在实践中应用理论知识，提高实践能力，积累经验，不断拓展视野，提高解决水利问题的能力。

表6 各指标的权重

总结该算法模型系统的特点如下：

1) 实现了人机交互，充分发挥了人与计算机各自的优势；

2) 群体专家的意见得以收敛；

3) 采用编码作为运算对象，为一些无数值概念或很难有数值概念的复杂决策问题提供了一种解决方法；

4) 该算法模型所采用的交互式遗传算法从有多个个体组成的初始群体开始搜索，相比传统的优化方法提高了搜索效率；

5) 采用层次分析法进行群体评价，将水利人才评价的定性指标定量化，将经过运算后的综合评分作为个体适应度值，实现了交互式遗传算法与群体评价方法的有效结合。

4 结束语

针对水利人才评价问题提出了一种基于交互式遗传算法的群体评价模型，详细给出了算法的两个主要模块——交互式遗传算法模块和群体评价模块。以个体适应度值作为连接点将两个模块结合起来，人机交互的遗传算法充分发挥了人机各自的优势，实现了从定性评价到定量评价的有效转换，并且提高了搜索最优解的效率。通过Matlab技术构建仿真模型，成功地应用于水利人才的群体评价。实验结果表明这一模型是可行的，并且得到的结果满足专家的要求，是一种有效的群体评价模型，为水利人才评价这种复杂的决策问题提供了一种解决方法。

[1] 宋东明，朱耀琴，吴慧中.基于交互式遗传算法模型的群体论证方法[J].中国工程科学，2009,11:66-71，80.

[2] 徐恭学.筛选式群体评价模型及算法[J].数学的实践与认识，1999，29(4)：21-26..

[3] 水利部.现代水利人才需求与培养[EB-OL].[2014-10-20].http://www.gov.cn/gzdt/2008-10/11/content1117708.htm.

[4] 付显惠.基于企业职业技术人才评价研究与应用[J].辽宁工业大学学报:自然科学版,2010(2):60-65.

[5] 吴洁，陈卫.模糊决策在基础研究创新群体评价中的应用[J].科技进步与决策，2002(11):122-123.

[6] 黄深泽.一种模糊多属性的群体评价方法[J].科技与管理，2005(2):38-40,44.

[7] 张发明，郭亚军，张连怀.一种多阶段交互式群体评价方法[J].管理学报，2010(9):158-162.

[8] 张发明.一种主客方交互式群体评价方法及其应用[J].管理学报，2011(11):144-148.157.

[9] 孙晓燕，王煦法，巩敦卫.分布协同交互式遗传算法及其在群体决策中的应用[J].信息与控制，2007(5):31-35.

[10]巩固，黄永清，郝国生.交互式遗传算法的改进方法及应用[J].计算机工程，2009(1):171-173.

[11]尤海峰，王喜玮，徐翔,等.一种多用户交互式遗传算法及其在群体设计中的应用[J].中国科学技术大学学报，2010(4):98-103.

[12]郭广颂，赵绍刚.基于个体适应值灰模型的交互式遗传算法[J].计算机工程，2010(3):215-218.

[13]胡晓辉，陈俊莲，张晓颖.改进的区间值模糊集交互式遗传算法[J].计算机工程与应用，2010,28:55-57.

[14]胡静，李金龙，陈恩红,等.交互式遗传算法中用户评估方法研究[J].小型微型计算机系统,2001,22(5):562-564.

[15]吴大亲，么文学.基于层次分析法的应用型人才培养评价模式研究[J].长春师范学院学报:自然科学版,2010(8):33-36.

(责任编辑 杨黎丽)

Group Evaluation Model Based on Interactive Genetic Algorithm：Taking Talents of Water Conservancy as an Example

MA Rui-min, BIAN Yi-jie, WU Hui

(Business School, Hohai University, Nanjing 211100, China)

A group evaluation model based on interactive genetic algorithm was proposed according to the complex decision-making problem of water conservancy talent evaluation. It realized the combination of group evaluation methods with interactive genetic algorithm by the individual’s fitness. It solved the non-quantitative of optimization targets of the complex decision-making of this kind water conservancy talent evaluation by combining human subjective evaluation with computer technology and quantifying the qualitative index through applying the artificial intelligence techniques. The group evaluation system based on interactive genetic algorithm was developed in the Matlab environment and adopted in the water conservancy talent evaluation. The experimental results show that this algorithm provides a solution for this kind of complex and fuzzy decision-making problem because it is feasible and effective in the group evaluation.

interactive genetic algorithm; group evaluation; analytic hierarchy process; water conservancy talent

2014-10-15 基金项目：国家自然科学基金资助项目(61170089)

马瑞敏(1989—),女,河南新乡人,硕士研究生,主要从事信息管理与电子商务研究；卞艺杰 (1964—),男,江苏南通人,博士,教授,主要从事信息管理与电子商务研究。

马瑞敏,卞艺杰,吴慧.基于交互式遗传算法的群体评价模型——以水利人才为例[J].重庆理工大学学报：自然科学版，2015(3):71-77.

format：MA Rui-min, BIAN Yi-jie, WU Hui.Group Evaluation Model Based on Interactive Genetic Algorithm：Taking Talents of Water Conservancy as an Example[J].Journal of Chongqing University of Technology:Natural Science,2015(3):71-77.

10.3969/j.issn.1674-8425(z).2015.03.014

TP18

A

1674-8425(2015)03-0071-07