基于Choquet 积分的电力网络规划方案评估

章 侃，文福拴，2，胡列翔，徐 谦，兰 洲，曾平良

(1． 浙江大学电气工程学院，杭州市310027;2． 文莱科技大学电机与电子工程系，斯里巴加湾市BE1410;3． 国网浙江省电力公司，杭州市310007;4． 国网浙江省电力公司经济技术研究院，杭州市310008;5． 中国电力科学研究院，北京市100192)

0 引 言

电力网络规划从总体上可分为规划方案形成和规划方案优选2个阶段。在方案优选阶段，采用相应的评价指标体系对各待选规划方案进行评价得到综合评价结果，然后排序选出综合最优的电力网络规划方案。

针对电力网络规划方案综合评价问题，国内外已经做了一些研究工作。文献［1］采用层次分析法(analytic hierarchy process，AHP)对分布式电源规划进行方案优选;文献［2］采用熵权法和灰色关联分析法对输电系统规划方案进行评价和优选;文献［3-4］分别采用模糊决策方法和区间熵方法对输电系统规划方案进行评价。上述文献所采用的评价指标体系中，所包含的评价指标具有关联性，但所采用的综合评价方法并没有对这种关联性进行适当处理。文献［5］采用多属性网络层次组合方法，对智能电网进行综合评价;文献［6］采用网络分析法，对含高渗透率间歇性电源的电力系统网络规划方案，进行评价和优选。文献［5-6］均采用了网络分析法来构建指标权重矩阵，虽然考虑了指标间的关联性，但在构建指标网络结构的过程中需全面考虑指标间的关联反馈关系，这对于指标数量较多的问题，计算负担很重，且所有关联指标之间的相对权重也不易确定。

目前比较常用的规划方案综合评价方法以期望效用理论为基础，对指标采用线性加权求和的方式得到综合评价结果。然而，具有关联性的指标未必符合线性关系，亦即未必可加，此时综合评价问题原理上就属于非线性期望问题。在此背景下，本文提出一种基于Choquet 容度积分的综合评价方法。利用Choquet 容度对不可加的关联指标进行测度，然后采用Choquet 非线性积分求取综合评价结果。

在衡量规划方案收益的不确定性方面，目前的研究成果主要集中在客观风险领域。已经提出了一些风险评估指标，如尾部条件期望(tail conditional expectation)、风险价值(value at risk，VaR)、条件风险价值(conditional value at risk，CVAR)等［7］。在对规划方案进行评价时，现有方法一般不考虑决策者的主观风险偏好，而这可对决策结果产生明显影响。在此背景下，本文采用合适的效用函数刻画决策者的风险偏好，利用基于Choquet 积分的风险溢价度量决策者为消除风险愿意减少的回报量，然后求取考虑了决策者风险偏好的主观预期综合收益作为经济性指标的综合评价结果。然后，把经济性指标和可靠性指标评价结果综合考虑，建立决策参考表。最后，用算例对所提出的方法进行说明。

1 传统期望效用理论

对于某一投资组合{S1，S2，…，Si，…，Sk}(i=1，2，3，…，k)，k 为该投资组合中的投资项目数。用pi表示投资组合内第i个项目能够获得收益yi的概率(i=1，2，3，…，k);u(yi)表示在收益yi下，该项目所能获得的效用。这样，该投资组合的期望效用可以表示为

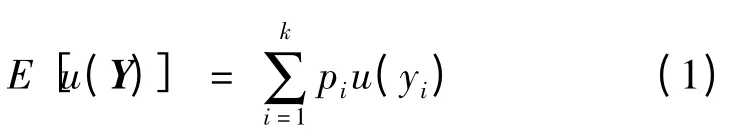
式中:Y =［y1，y2，…，yi，…，yk］;u(Y)为效用函数。

当有多种不同的投资组合时，决策者一般选择使E［u(Y)］最大的投资组合。由式(1)可知，期望效用是各分项效用以概率加权后的线性求和，其适用的前提是各分项项目之间完全独立，亦即其中任一项目收益不受其他项目收益的变化而变化。然而，对于实际投资问题，各分项项目未必完全独立，因此在期望效用理论的应用实践中出现了著名的Allais 悖论和Ellsberg 悖论［8］。这2个悖论均表明在决策过程中需要注意非可加的不确定性问题。现有的电力网络规划方案评估方法一般是以传统期望效用理论为基础的，没有考虑指标之间存在的关联性。

基于期望效用理论的决策机制还存在以下问题:(1)决策过程是静态的，即决策者主要依赖最终的效用值，而没有考虑目标的变化量;(2)没有考虑决策者的风险偏好差异。前一个问题即为引言中所述的客观风险问题，已经有了些研究报道并提出了一些方法，但现有方法主要基于统计分析且对决策对象的概率分布有较高要求;当决策对象不满足特定的概率分布时，就会导致误差，本文不对此展开讨论。后一个问题即为引言中所提到的主观风险偏好问题，系本文的研究重点。

2 Choquet 积分和风险溢价

对于 Allais 悖论和 Ellsberg 悖论，可以由Choquet 提出的非可加测度即容度(capacity)概念来解释［8-9］。在提出容度概念之后，Choquet 进一步提出了有界随机变量关于容度的积分，即Choquet 积分［10-13］。Choquet 积分是非线性的，在经济、金融、决策理论等领域逐步得到广泛应用，也适用于解决电力网络规划方案评价中的指标关联性问题。

2.1 容度

给定状态空间Ω，其幂子集为2Ω，集类F⊂2Ω，称集函数μ:F→［0，1］为容度，如果满足:(1)μ(φ)=0，μ(Ω)=1;(2)μ(A)≤μ(B)，∀A，B∈F，且A⊆B。则称三元组合(Ω，F，μ)为一容度空间。

2.2 Choquet 积分

Choquet 给出了有界随机变量关于容度的积分［10-13］。给定随机变量f :(Ω，F)→［R，B(R)］，其中B(R)是R 的Borel σ-域。所有有界随机变量的全体记作L∞。假设f∈L∞，f 在A∈F 上关于容度μ的Choquet 积分记为

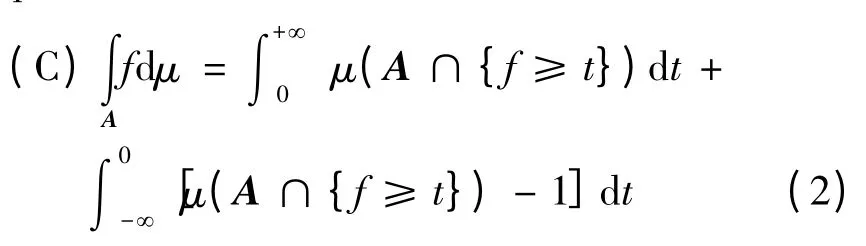
式中:(C)表示该积分为Choquet 积分。

2.3 效用函数与风险溢价

不同决策者对风险的态度一般也不同，总体上可分为3 类，即风险厌恶、风险中性或者风险喜好。决策者会根据自己的风险偏好进行决策。电网投资规模巨大，且工程建成后期望的使用年限可达几十年。因此，决策要非常慎重，期望的投资收益要比较稳定。这样，可以把电力网络规划决策者描述为风险厌恶类，采用凹的、增的效用函数u 来刻画。

行为金融学主要研究投资者的风险偏好，通常采用效用函数，包括引入财富偏好的效用函数［13］和引入习惯的效用函数［14］。财富偏好是指投资者通过占有财富来获得效用，而习惯偏好则关注决策者过去的投资经验。电力网络规划决策者的偏好往往依赖于其过往的工作经验，因此可采用引入习惯偏好的效用函数来刻画决策者的风险偏好。

效用函数可用下式来描述:

式中:ct表示最终财富值;ht为习惯参数，若γ 为0，则ht恒为1，γ 的取值由决策者根据历史经验确定;α 为风险厌恶系数，α ∈(0，1)，α 越大则表示决策者越厌恶风险，其值可根据决策者的风险厌恶程度确定。

在上述工作的基础上，进一步采用风险溢价来度量决策者风险偏好在收益上的反映。风险溢价是衡量为得到确定回报而情愿减少的期望回报量，Pratt 和Arrow 对风险溢价方面的研究做了基础工作，下面给出基于Choquet 积分的风险溢价计算方法［8］。

令μ 是(Ω，F)上的容度，如果收益组合X :Ω→R 是有界随机变量，则X 的Choquet 期望值定义为

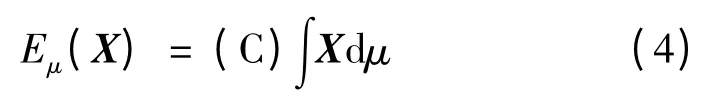
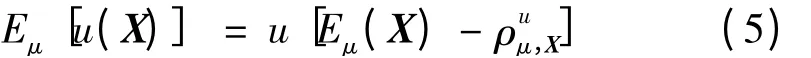
如果效用函数u 是严格增函数，则有

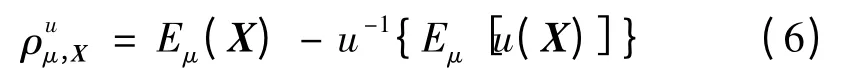
式中:u－1为u 的反函数。

3 基于Choquet 积分的规划指标评估

一般采取经济性与可靠性相结合的指标评价体系来评估电力网络规划方案［15-17］。经济性指标主要用来衡量电力网络投资的预期收益，随着社会及企业自身对其在环境保护和社会贡献方面的重视，决策者在考虑预期收益时也会适当考虑外部收益，故可将电力网络投资的预期收益分为内部收益和外部收益。内部收益指企业获得的货币收益，外部收益包括社会收益和环境收益。可靠性指标主要用来衡量所规划的电力网络的运行可靠性，包括失负荷概率、电量不足期望、失负荷平均持续时间和电压水平。在文献［15-17］的基础上，可建立图1 所示的规划方案评价体系。

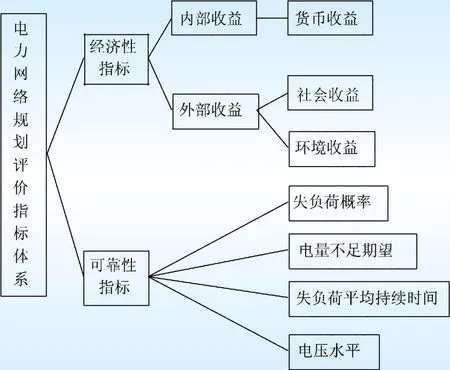
图1 电力网络规划评价指标体系Fig.1 Evaluation index system of power network planning

货币收益表示实施该规划方案可获得的净收益，采用净现值来度量;社会收益表示实施该规划方案对社会的贡献，采用纳税额来度量;环境收益表示规划方案的环境友好程度，可由污染物减排效益来度量。可靠性指标则采用可靠性分析软件求取。

离散形式的Choquet 积分计算式为

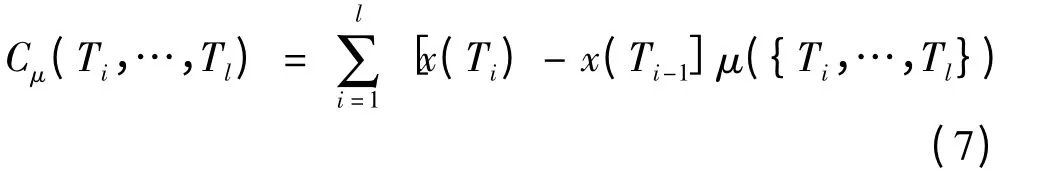
式中:Ti表示指标(i =1，2，3，…，l;l 为指标总数);x(Ti)表示对应的指标值，x(T0)=0;μ({Ti，…，Tl})表示{Ti，…，Tl}的容度;指标全集的容度μ({Ti，…，Tl})= 1 。

令{P1，P2，P3}表示经济性指标集合，P1、P2和P3分别表示货币收益、社会收益和环境收益;令{Q1，Q2，Q3，Q4}表示可靠性指标集合，Q1、Q2、Q3和Q4分别表示失负荷概率、电量不足期望、失负荷平均持续时间和电压水平。同类指标的容度，在这里表现为指标子集的权重。由Choquet 积分的离散公式可知，计算Choquet 积分时只需知道部分指标子集的容度，而专家以往的决策和工程经验为确定容度积累了一定的经验，因此在本文中经济性和可靠性指标的容度可由专家根据领域知识和经验确定。然后，根据经济性指标{P1，P2，P3}、可靠性指标{Q1，Q2，Q3，Q4}及相应容度，求取未考虑风险偏好的经济性综合评价结果CE以及可靠性综合评价结果CR。

4 基于风险溢价的电力网络规划方案决策

决策者对货币收益一般具有风险偏好。外部收益作为企业的社会责任，在相当程度上具有客观性，故假设决策者对社会收益和环境收益不具有风险偏好。首先采用式(3)可得到某给定规划方案的货币收益效用，之后利用风险溢价公式求得该方案下的风险溢价。则消除了风险溢价后的主观预期综合收益可表示为

主观预期综合收益即为规划方案最终的经济性指标综合评价结果，其中容纳了决策者的风险偏好。不同的决策者的风险厌恶系数一般不同，风险溢价和主观预期综合收益也就不同。针对一系列电力网络规划方案，求得不同决策者的主观预期综合收益，那么m个决策者在n个方案下的主观预期综合收益可用矩阵CS表示:

以D1，D2，…，Dm表示这m个决策者，那么对决策者Dj(j =1，2，…，m)而言，其对方案的最优选择结果应为式(9)中第j 行的最大值所对应的规划方案。

本报讯 为进一步利企便民，为企业和群众提供多渠道、便利化服务，近日，农业农村部行政审批手机客户端“益农e审”App正式上线运行。

在实际决策时，还需要考虑可靠性指标的综合评价结果:

则根据式(9)和式(10)，建立供决策者参考的决策表，如表1 所示。

根据表1，具有不同风险偏好的决策者，对不同规划方案间的主观预期综合收益和可靠性指标综合评价结果，进行综合考量后最终决策。

表1 决策参考表Table 1 Decision-making reference table

5 算例分析

采用文献［18］中针对巴西南部46 节点电力系统的2个电力网络规划方案，来说明所提出的基于Choquet 积分的电力网络规划方案综合评价与决策方法。所采用的规划评价原始数据参见附录。对备选规划方案的初步评价结果如表2 所示。

表2 2个备选规划方案的评价结果Table 2 Evaluation results of two alternative planning schemes

从表2 中可以看出，方案I 和方案Ⅱ的经济性和可靠性指标均有差异;方案I 的货币收益低于方案Ⅱ，社会收益和环境收益优于方案Ⅱ;方案I 的各项可靠性指标除失负荷概率外，均优于方案Ⅱ。

经济性指标全集的容度为1，即μ({P1，P2，P3})=1。根据Choquet 积分的离散公式，可知求取Choquet 积分只需知道部分指标子集的容度。专家根据领域知识和经验确定的容度为:μ({P2，P3})=0.32，μ(P3)=0.17。

给定D1、D2和D3这3个决策者的风险厌恶系数α 分别为0.45、0.50 和0.62。在本算例中主要考虑了风险厌恶系数，给定习惯系数均为1。

将表2 中的数据以及上述数据代入式(3)、(6)和(7)，计算得到的风险溢价如表3 所示。

然后，将可靠性指标进行归一化处理。可靠性指标全集的容度为1，即μ({Q1，Q2，Q3，Q4})=1。专家根据领域知识和经验确定的可靠性指标的容度为:μ({Q2，Q3，Q4})=0.79，μ({Q3，Q4})=0.46，μ(Q4)=0.12。

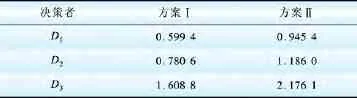
表3 风险溢价Table 3 Risk premiums 亿元

采用Choquet 容度积分计算得到方案I 和方案Ⅱ的可靠性指标综合评价结果分别为0.989 1和0.922 0。

基于上述结果，可建立表4 所示的决策参考表。

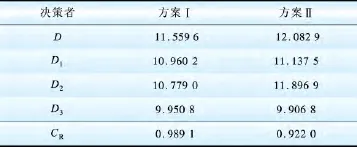
表4 决策参考表Table 4 Decision-making reference table 亿元

由文献［18］可知，方案I 和方案Ⅱ的总投资以人民币计价分别为28.701 0 亿元和25.706 8 亿元，方案I 的总投资比方案Ⅱ高，但其可靠性也高于方案Ⅱ。根据决策参考表，在未考虑风险偏好的情况下，方案I 的经济性指标要比方案Ⅱ差;方案I的可靠性指标要优于方案Ⅱ，这与文献［18］的结论一致。

根据决策参考表，对于无风险偏好的决策者，虽然方案Ⅱ的可靠性指标比方案I 低，但从经济性指标看，方案Ⅱ的主观预期综合收益要明显高于方案I，决策者倾向于选择方案Ⅱ。决策者D1、D2、D3的风险厌恶系数排序为α1＜α2＜α3，随着风险厌恶程度的加大，决策者对于这两个方案的主观预期综合收益也越来越接近。对于决策者D1，方案Ⅱ的主观预期综合收益只比方案I 高0.177 3 亿元，考虑到方案I 的可靠性更高，D1倾向于选择方案I。对于决策者D2，方案Ⅱ的主观预期综合收益仅比方案I高出0.117 9 亿元，故D2更倾向于选择方案I。对于决策者D3，方案I 的主观预期综合收益高于方案Ⅱ，故其最优决策是方案I。

文献［18］得到的结论为:决策者考虑到虽然方案I 的投资额更大，但方案I 的可靠性指标要优于方案Ⅱ，故选择方案I，这其实已经考虑了决策者对预期收益的风险厌恶态度。本文得到的结论与文献［18］的结论一致。

6 结 语

本文所提出的电力网络综合评价方法将容度理论应用于消除测度非可加的指标之间存在的关联性，然后采用Choquet 非线性积分计算指标的综合评价结果，消除了指标间关联性对综合评价的影响;将基于Choquet 的风险溢价应用于经济性综合评价，考虑了不同决策者在面对方案收益不确定性时所具有的风险偏好。算例结果表明，所提出的综合评价方法和建立的决策表有助于对电力网络规划方案进行合理评价和优选。

［1］杨琦，马世英，宋云亭，等． 分布式电源规划方案综合评判方法［J］． 电网技术，2012，36(2):212-216．Yang Qi，Ma Shiying，Song Yunting，et al． Comprehensive evaluation of distributed generation planning scheme［J］． Power System Technology，2012，36(2):212-216．

［2］罗毅，李昱龙． 基于熵权法和灰色关联分析法的输电网规划方案综合决策［J］． 电网技术，2013，37(1):77-81．Luo Yi，LI Yulong． Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis［J］． Power System Technology，2013，37(1):77-81．

［3］王瑞莲，赵万里． 基于模糊决策的城市高压输电网规划方案评价方法［J］． 电网技术，2013，37(2):488-492．Wang Ruilian，Zhao Wanli． A fuzzy decision-based method to evaluate planning scheme for urban high voltage transmission network［J］． Power System Technology，2013，37(2):488-492．

［4］肖雪，林振智，文福拴，等． 含风电的输电系统规划方案优选的区间熵方法［J］． 电力系统及其自动化学报，2013，25(6):16-24．Xiao Xue，Lin Zhenzhi，Wen Fushuan，et al． Interval entropy method for selecting the best transmission planning scheme with wind power accommodated［J］． Proceedings of the CSU-EPSA，2013，25(6):16-24．

［5］孙强，葛旭波，刘林，等． 智能电网多属性网络层次组合评价法及其应用研究［J］． 电网技术，2012，36(10):49-54．Sun Qiang，Ge Xubo，Liu Lin，et al． Multi-attribute network process comprehensive evaluation method for smart grid and its application［J］． Power System Technology，2012，36(10):49-54．

［6］王深哲，高山，李海峰，等． 含高渗透率间歇性电源的电网规划方案优选方法［J］． 电网技术，2013，37(8):2129-2135．Wang Shenzhe，Gao Shan，Li Haifeng，et al． Optimal selection of planning schemes for power grid with high penetration of intermittent generation［J］． Power System Technology，2013，37 (8 ):2129-2135．

［7］Zenios S A． Practical financial optimization:decision making for financial engineers［M］． Oxford，UK:Blackwell，2008．

［8］王洪霞．Choquet 积分和集值Choquet 积分及其在金融中的应用［D］． 北京:北京工业大学，2013．Wang Hongxia． On Choquet integral and set-valued Choquet integral with their applications in finance［D］． Beijing:Beijing University of Technology，2013．

［9］Klement E P，Mesiar R，Pap E． A universal integral as common frame for Choquet and Sugeno integral［J］． IEEE Transactions on Fuzzy Systems，2010，18(1):178-187．

［10］Sugeno M．A way to Choquet calculus［J］． IEEE Transactions on Fuzzy Systems，2015，23(5):1439-1457．

［11］Denneberg D． Non-additive measure and integral［M］． Boston:Kluwer Academic Publishers，1994．

［12］Denneberg D．Conditioning (updating)non-additive measures［J］．Annals of Operations Research，1994，52(1):21-42．

［13］Bakshi G S，Chen Z W． The spirit of capitalism and stock market prices［J］． American Economic Review，1996，86(1):33-157．

［14］Abel A B．Asset prices under habit formation and catching up with the joneses ［J］． American Economic Review， Papers and Proceedings of the Hundred and Second Annual Meeting of the American Economic Association，1990，80(2):38-42．

［15］姚建刚，何井龙． 电力市场环境下的输电网扩展规划［J］． 电力系统及其自动化学报，2010，22(5):135-140．Yao Jiangang，He Jinglong． Transmission expansion planning in an electricity market［J］． Proceedings of the CSU-EPSA，2010，22(5):135-140．

［16］高山，王深哲，李海峰，等． 基于前景理论的电网规划方案综合决策方法［J］． 电网技术，2014，38(8):2029-2036．Gao Shan，Wang Shenzhe，Li Haifeng，et al． Prospect theory based comprehensive decision-making method of power network planning schemes［J］． Power System Technology，2014，38(8):2029-2036．

［17］谭伟，何光宇，刘锋，等． 智能电网低碳指标体系初探［J］． 电力系统自动化，2010，34(17):1-5．Tan Wei， He Guangyu， Liu Feng， et al． A preliminary investigation on smart grid's low-carbon index system ［J］．Automation of Electric Power Systems，2010，34(17):1-5．

［18］郑静，文福拴，李力，等． 计及风险控制策略的含风电机组的输电系统规划［J］． 电力系统自动化，2011，35(22):71-76．Zheng Jing，Wen Fushuan，Li Li，et al． Transmission system planning with risk-control strategies for power systems with wind generators［J］．Automation of Electric Power Systems，2011，35(22):71-76．