基于相关积分优化方法的裂解炉优化

刘春平，王昕，王振雷

（1华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海200237；2上海交通大学电工与电子技术中心，上海 200240）

基于相关积分优化方法的裂解炉优化

刘春平1，王昕2，王振雷1

（1华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海200237；2上海交通大学电工与电子技术中心，上海 200240）

裂解炉是石油化工产业中重要设备，优化裂解炉运行状态对提升乙烯装置绩效至关重要。由于裂解反应机理复杂，裂解炉模型难以确定且扰动频繁，运用传统优化方法难以解决裂解炉运行优化问题。提出将相关积分优化方法应用于裂解炉运行优化，以解决裂解炉优化需要裂解炉具体模型、传统优化方法的自适应性与抗干扰性不满足裂解炉优化需求的两大问题。首先，分析影响裂解炉运行的主要操作参数，选取合适的操作变量，并构建优化目标函数；然后，采集操作变量与优化目标函数数据，建立裂解炉历史数据库。最后，基于相关积分优化方法，利用历史数据进行迭代计算以对裂解炉进行优化。仿真结果验证了相关积分优化方法在裂解炉优化中的有效性。

算法；裂解炉；模型；操作变量；测量；目标函数

Key words: algorithm; cracking furnace; model; operating variable; measurement; optimal objective function

引 言

石油化工产业是我国支柱产业之一，乙烯、丙烯是石油化工产业中最重要的产品。乙烯、丙烯的产量、生产规模、生产技术标志着一个国家石化工业的发展水平。裂解炉作为整套石油化工设备的龙头装置，对整个化工过程的平稳运行以及能耗物耗，甚至最后总的经济效益有着极为重要的影响。

为此，李平等[1]研究了乙烯裂解炉先进控制系统的开发与应用。王灵、宋辰等[2-3]先后基于自适应量子蚁群算法与免疫文化算法对裂解炉进行了故障诊断。耿志强等[4]于2010年提出了基于多群竞争PSO-RBFNN的乙烯裂解深度智能优化控制方法，避免了裂解炉优化陷入局部最优，提高了算法的全局搜索能力。2013年，Nian、商保鹏等[5-6]相继对裂解过程中切料时机选择的问题进行了研究，显著提高了裂解炉的运行效益。盛杰等[7]对裂解炉裂解过程建模与优化进行了研究。此外，2014年周书恒等[8]提出基于迁移学习的方法对裂解炉进行建模，以在少量新数据的情况下充分挖掘了历史数据中包含的信息，取得了很好的应用效果。

然而，传统的优化方法必须针对具体工艺装置进行建模，建立的优化模型也具有特定适用性。运用传统优化方法，当裂解炉设备老化、更替、催化剂改良后，都需重新建模或对模型进行修改。此外，裂解炉工艺过程扰动频繁，对传统优化方法自适应性与抗干扰性要求太高。如何解决模型的建立、克服工艺过程扰动，对裂解炉进行优化，以提高“双烯”（乙烯、丙烯）收率、进而获得更大的经济效益，是石油化工工业发展中一个亟需解决的命题。

相关积分法是1983年Grassberger和 Procaccia[9]在Takens[10]介绍的延时重构理论的基础上首先提出来的。相关积分法应用于故障诊断与预报监控效果显著。2003年，Zhao等[11]把相关积分作为一个特征集合，第一次提出了基于相关积分法的诊断方法。2004年，朱俊玲等[12]研究了相关积分法预报癫痫发作方面的应用。2006年，孙涛等[13]针对离心风机的喘振问题，在研究相关积分算式参考距离取值原则的基础上，提出了一种经验模式分解法(EMD)结合相关积分法的喘振先兆辨识方法；吴云等[14]研究了某轴流式压气机节流试验中的气动不稳定问题。相关积分法也应用于过程控制优化。冯建等[15]重点论述了抚顺石油二厂流化催化裂化装置利用相关积分算法进行优化控制的实施方法。在一种多输入多输出连续生产过程的实时操作优化方法专利中，提出了根据生产过程关键操作条件和技术指标的历史数据，利用相关积分法在线计算出关键操作条件与技术指标之间在当前时间的梯度向量，根据梯度向量来确定操作条件的调整方向，使技术指标达到最优的优化方法[16]。张韶煜等[17]将相关积分优化方法应用到芳烃装置反应器控制。相关积分优化方法只需要当前操作点附近的输入输出信息，不依赖具体的模型，可以省去复杂的建模过程，这给优化带来了极大方便。

本文将相关积分优化方法应用于裂解炉优化，以解决裂解炉优化需要裂解炉具体模型以及传统优化方法的自适应性与抗干扰性不满足裂解炉优化需求的两大问题。主要内容如下：分析裂解炉运行情况，提取影响裂解炉绩效的主要操作参数，以油品属性、平均出口温度COT、汽烃比、进料流量为操作变量，裂解炉双烯收率、经济效益为优化目标函数，利用相关积分优化方法，对裂解炉进行优化。

1 相关积分优化方法

相关积分优化方法是一种与随机过程相关的运算。在相关积分理论中，干扰、操作变量、目标函数都被看作为随机过程，操作变量均为可控变量。

首先确定目标函数()J t，该目标函数应是在线可测量的或者在线可计算的，可表示为

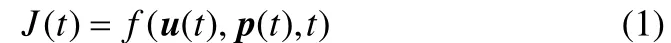
式中，()tu为m维可控操作变量，()tp为干扰变量，f为未知映射。在一定条件下，目标函数与操作变量的梯度k满足以下关系式

式中，()tε是均值为0的噪声项。Juk是操作变量与目标函数之间的互相关积分向量，定义为

其中iuJk按公式（4）计算

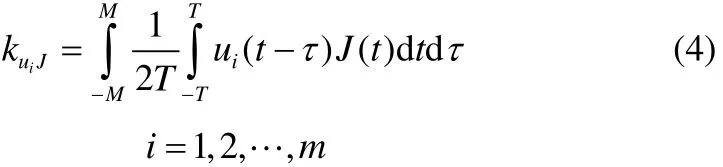
同时，uuk为操作变量自相关积分矩阵，定义为

且ijuuk按公式（6）计算

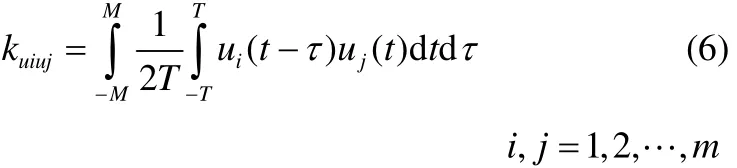
在式（4）与式（6）中，T，M一般取大于0的积分常数。根据相关积分理论，M应当大于从操作变量到目标函数的最大的时间常数。T通常取1～5倍M。ui(t)(i=1,2,…,m)、J(t)分别为操作变量和目标函数的测量值。根据公式（3）～公式（6），kuJ、kuu可通过操作变量和目标函数的观测值计算得到，然后依据公式（2）可求出目标函数的梯度k。在得到目标函数梯度k后，根据式u(l+1)=u(l)+αku(l)直接迭代计算操作变量新的设定值u(l+1)。α通常取常数。

本文采用自适应步长参数α值，使其满足

式中，k为计算得出的目标函数的梯度，k0为首次计算得出的目标函数的梯度。0α为常数。如果优化目标为求极大值问题，则00＞α，如果优化目标为求极小值问题，00＜α。0α大小依据现场的收敛速度来取值。迭代过程在线持续进行，直到梯度k为0。

2 相关积分优化方法步骤

本文相关积分优化方法流程如图1所示。

相关积分优化方法步骤如下：

（1）根据工艺过程需要，确定多个优化目标函数J1,J2,…,Jn与操作变量u1,u2,…,um，并构造一个综合目标函数J=σ1J1+σ2J2+…+σnJn。其中，σ1,σ2,…,σn为各个目标函数的加权系数。根据工艺要求，取其为0到1之间。

（2）根据工艺过程时间特性，采集各操作变量和各目标函数数据，建立具有一定数据宽度的实时数据库。在每一个数据库更新时刻，新的采样数据添加到数据库，数据库中最老时刻采样数据被剔除。

（3）利用每一采样时刻更新后的数据库，根据公式（5）、公式（6）计算各操作变量自相关积分矩阵kuu。

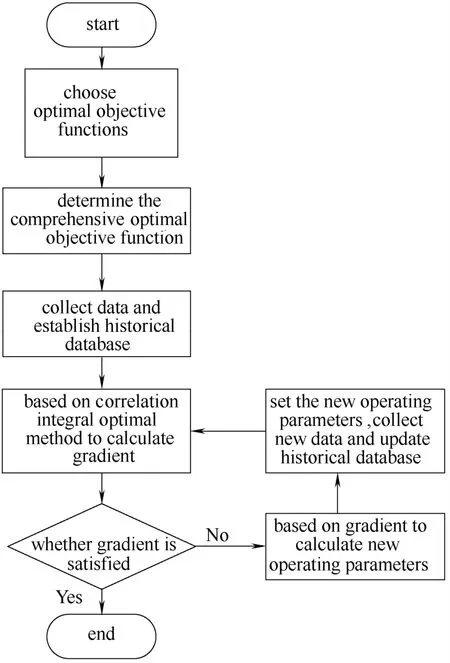
图1 相关积分优化方法流程Fig.1 Diagram of correlation integral optimal method

（4）计算各操作变量与目标函数的互相关积分矩阵uJK。若有n个目标函数，则

式中

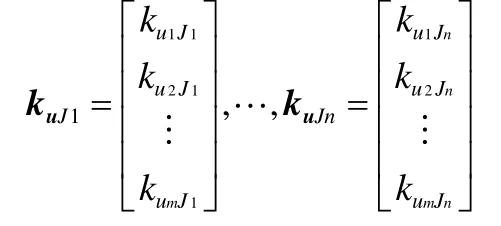
且uiJjk按公式（4）计算。

（5）根据自相关积分矩阵和互相关积分矩阵，计算操作变量对综合目标函数的梯度向量。通过以下方式得到：首先根据公式（9）求出dK

式中，uJK满足公式（8）、uuK满足式（10），且公式（10）中uuk满足公式（5）。

则计算得到的dK满足如下形式

综合目标函数J对操作变量的梯度为

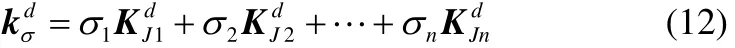
（6）根据梯度向量，计算操作变量新值。若梯度向量为0，表明操作变量已在最优状态。若不为0，操作变量则按梯度进行调整。通常按公式（13）进行操作变量调整。

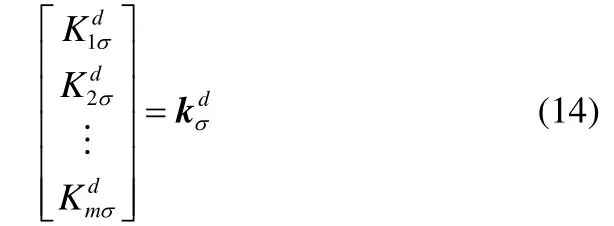
且α1,σ2,…,αm为m个满足式（7）的因子（α0可取m个不同的值αi,0）。则第i个操作变量ui的调整步长为αiui(l)。基于自适应参数αi的值调整步长大小与方向。

（7）设置操作变量新值，采集新的数据，并将新的采集数据添加到数据库，数据库中最老时刻数据被丢弃，转步骤（3）。

3 相关积分优化方法在裂解炉优化中的研究

3.1 裂解炉工艺介绍

在石油化工装置中，乙烯裂解炉是关系到整个石油化工装置平稳运行以及能耗物耗的关键设备，对最后石油化工生产过程总的经济效益有着重要作用。

在整个工业热裂解过程中，其反应过程可分为生产所期望的小分子烯烃和烷烃的一次反应，以及由一次反应生成的乙烯丙烯继续反应生成炔烃、二烯烃、芳烃，甚至结焦生炭的不利于生产的二次反应[18]。恰当的裂解深度能够最大限度地促进一次反应而抑制二次反应，从而提高燃料的利用率与原料的利用率，进而提高双烯收率与经济效益。裂解炉的操作优化是指通过对影响裂解过程的某些关键过程工艺参数进行调整，从而使裂解炉在平稳安全运行的条件下达到某些设定的优化目标。

裂解炉双烯收率与油品属性、裂解炉平均出口温度COT、裂解炉汽烃比、进料流量、横跨温度等因素有关[19-22]。

3.2 相关积分优化方法在裂解炉双烯收率优化中的仿真

本文根据实际工况的变化情况，取油品密度范围为（0.65，0.75）（kg·L−1），NP/IP范围为（0.20，1.50），NP+IP范围为（60，100），COT范围为（816.75，843.35）（℃），汽烃比的范围为（0.495，0.6565），进料范围为（35，45）（t·h−1）。令T=100，M=50，数据库大小为301。采取301组裂解炉数据作为数据库初始数据。取平均出口温度最大的变化步长为0.1℃，汽烃比最大变化步长为0.0005，COT温度自适应步长参数α1,0=0.05，汽烃比自适应步长参数α2,0=0.005。

仿真时，每采样一次，数据库更新一次，并按相关积分优化步骤（3）～（7）进行一次相关积分优化计算。在每一次优化计算中，利用数据库中COT温度、气烃比、乙烯收率和丙烯收率的历史数据根据公式（3）～公式（6）与公式（8）计算得到kuu与KuJ。其中，公式（4）与公式（6）采用离散形式，kuu为操作变量（COT温度、气烃比）的自相关积分矩阵，KuJ为操作变量（COT温度、气烃比）与乙烯收率、丙烯收率的互相关积分矩阵按公式（8）排列后得到的矩阵。

当油品属性与进料流量状态按表1发生变化时，基于相关积分优化方法的裂解炉各优化曲线如图2～图6所示。其中，横坐标表示优化时进行的采样次数。

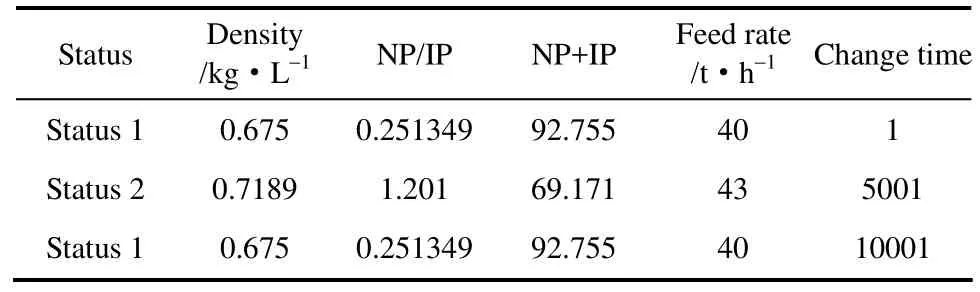
表1 油品属性与进料流量变化表Table 1 Changes of feedstock properties and feed rate

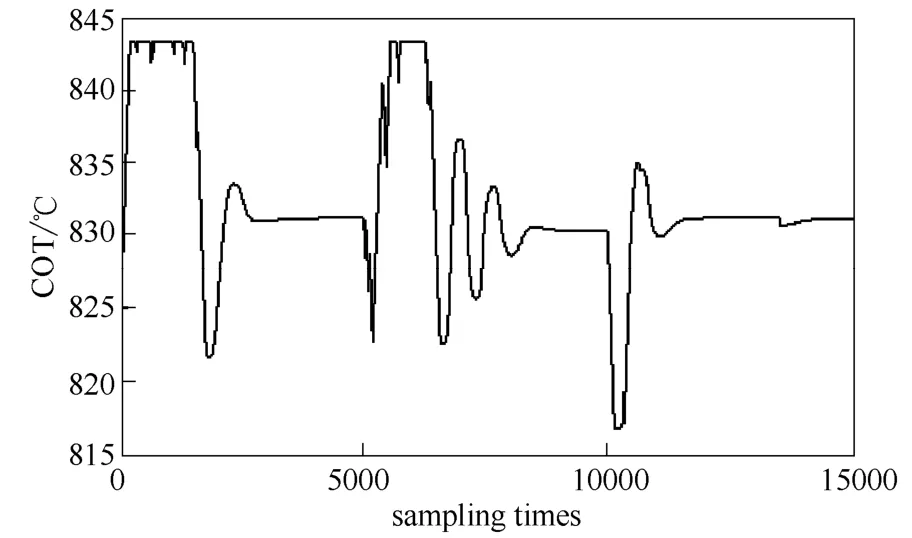
图2 COT温度优化曲线Fig.2 Curve of COT

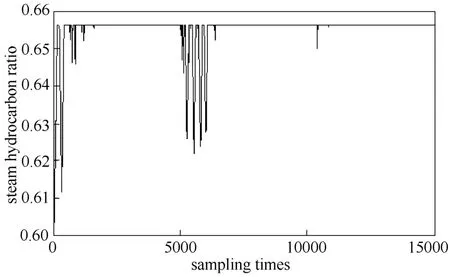
图3 汽烃比优化曲线Fig.3 Curve of steam hydrocarbon ratio

图4 乙烯收率曲线Fig.4 Curve of C2H4yield

图5 丙烯收率曲线Fig.5 Curve of C3H6yield

图6 双烯收率曲线Fig.6 Curve of dienes yield

基于相关积分优化方法优化得到相应状态下最优操作点如表2所示。此外，本文也对状态一采用了穷举法分析，以验证相关积分优化方法在双烯收率优化中的有效性。COT与汽烃比取不同值时的状态一的双烯收率结果如表3所示。

表2 基于相关积分优化方法的双烯收率最优状态值Table 2 Optimal status values of dienes yield based on correlation integral optimization method

通过表3可得，在同一COT下汽烃比取0.65时的双烯收率都大于汽烃比取0.63、0.64时的双烯收率，表明在COT相同时，汽烃比取较大值时双烯收率更大。在表3所列举的结果中，COT取831℃、汽烃比取0.65、双烯收率45.5525%为状态一的最优解，这表明状态一的实际最优解在COT为831℃、汽烃比为0.65附近。而在表2中，基于相关积分优化方法得出的状态一的最优COT为831.2566℃、汽烃比为0.6565、双烯收率为45.5928%，这与表3得出的结论相符，且当COT为831.2566℃、汽烃比为0.6565时，状态一的双烯收率大于表3中任何操作状态的双烯收率，因此基于相关积分优化方法得出的状态一的最优解是可靠的。此外，仿真中综合目标函数为双烯收率，故也可通过分析图6曲线判断相关积分优化方法在裂解炉优化中的有效性。在本次优化中，各变量都被约束在一定范围内，裂解炉的最优解是局部最优解。从图6中看到，对状态一优化时，双烯收率分别在采样进行3000次与11600次后基本不变，且通过比较优化过程中双烯收率的采样数值可得，双烯收率曲线稳定后双烯收率大于曲线稳定之前任一采样时刻的双烯收率，这表明在经过3000次或11600次优化计算后得到的COT与汽烃比即为裂解炉状态一的局部最优解。同理，在对状态二优化时，在8000次采样后优化得到的COT与汽烃比即为状态二的局部最优解。在本文研究中，并没有建立裂解炉生产过程的动态与静态模型，故图6结果表明了相关积分优化方法不需要事先建立生产过程的动态与静态模型，大大降低工艺过程操作优化过程的复杂性。

表3 不同COT与汽烃比时状态一的双烯收率Table 3 Dienes yield of status 1 based on different COT and steam hydrocarbon ratio

相关积分优化方法是基于大量历史操作数据寻找最优解，因此，单个采样时刻产生随机误差并不会对梯度的计算产生较大影响；本文中历史数据库采取实时更新方式，每一采样时刻，新的采样数据添加到数据库，数据库中最老时刻采样数据被剔除。当工况发生变化时，反映旧工况特性的数据会逐渐从历史数据库中被剔除，而体现新工况特性的数据被逐渐添加到历史数据库。当历史数据库全部更新为新工况下的采样数据时，基于相关积分优化算法迭代得到的最优解即为新工况下的最优操作点，从而具有自适应性。本文提出的自适应性主要表现在当工况发生变化时，如进料量、油品属性等变化，相关积分优化方法能重新找到最优解。表2给出了相关积分优化方法在不同操作状态下对裂解炉进行优化的最优COT与汽烃比。比较表2第一行与第二行可得，当裂解炉工作状态在不同操作状态之间切换时，相关积分优化方法能准确找到裂解炉最优COT与汽烃比；比较表2第一行与第三行可得，相关积分优化方法在同一操作状态下优化结果基本一致。因此，相关积分优化方法具有好的自适应性与抗干扰性。

此外，若COT变化1℃，其他条件不变，双烯收率变化约0.02个百分点；若汽烃比变化0.01，其他条件不变，双烯收率变化约0.07个百分点。但在表2中，状态一与状态二最优解的COT相差1℃、汽烃比相同，双烯收率最优值却相差约1个百分点，而影响裂解炉双烯收率的条件主要包括裂解原料（油品属性、进料量）、裂解操作条件（COT、汽烃比）与裂解炉炉型，表明裂解原料相关条件对双烯收率的影响比裂解操作条件对双烯收率的影响大。当工况由状态一切换到状态二，若不进行再次优化而继续采用状态一的最优解，此时的双烯收率通过计算为44.5975%，比状态二的最优双烯收率44.5999%少0.024个百分点，因此，当裂解炉油品属性与进料量变化时，对裂解炉再次进行优化是十分有必要的。所有状态的最优汽烃比均为其寻优范围上限0.6565，这表明在裂解炉工艺过程中，汽烃比取较大值更有利于提高双烯收率，这与实际裂解炉工艺原理相符。当裂解炉进料流量、油品属性变化时，相关积分优化方法都准确找到了使双烯收率最大的一组COT与汽烃比，故相关积分优化方法在裂解炉双烯收率优化中是可行的。

表4 经济效益优化参考价格表Table 4 Reference prices of economic benefit optimization

表5 经济效益状态表Table 5 Status values of economic benefit optimization

3.3 相关积分优化方法在裂解炉经济效益优化中的仿真

在裂解炉生产过程中，企业的目标是使裂解炉效益达到最大。裂解炉经济效益与乙烯、丙烯收率，乙烯、丙烯价格，原料油价格，燃料气消耗量，燃料气价格以及其副产品收率和其价格等因素有关。

令经济效益函数为

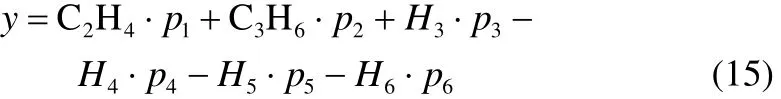
取油品密度范围为（0.60，0.80）（kg·L−1）、NP/IP范围为（0.20，1.5）、NP+IP范围为（60，100）、COT范围为（816.75，843.35）（℃）、汽烃比范围为（0.495，0.6565）、进料量范围为（35，45）（t·h−1）。在汽烃比取较大值更有利于提高双烯收率的情况下，寻找最优解即为寻找最优COT，故汽烃比在本次仿真中不进行优化。取COT最大的变化步长为0.1℃，COT温度自适应步长参数α1,0=0.001。取T=100，M=50，则数据库大小为301。

当取表4中价格、按表5中操作状态变化时，优化曲线如图7、图8所示，优化结果如表6与表7所示。

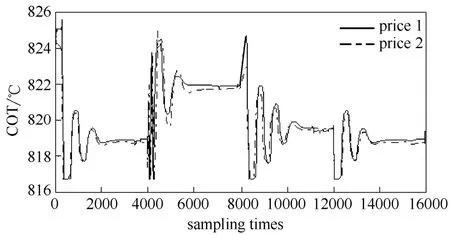
图7 经济效益优化COT曲线Fig.7 Curve of COT in economic benefit optimization

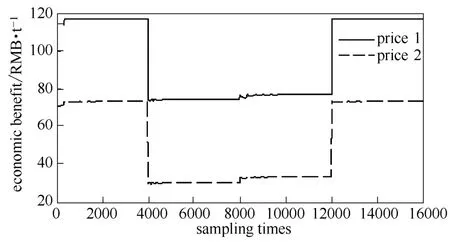
图8 经济效益曲线Fig.8 Curve of economic benefit

表6 经济效益优化COT优化结果Table 6 Results of COT in economic benefit optimization

在本次裂解炉经济效益优化的仿真中，当裂解炉进料流量、油品属性或价格变化时，相关积分优化方法都准确找到了使经济效益最大的COT，且相关积分优化方法在同一操作状态下优化结果也基本一致。在本次研究中，也没有建立裂解炉经济效益的动态与静态模型。本次仿真再次验证了相关积分优化方法在裂解炉应用中的有效性。

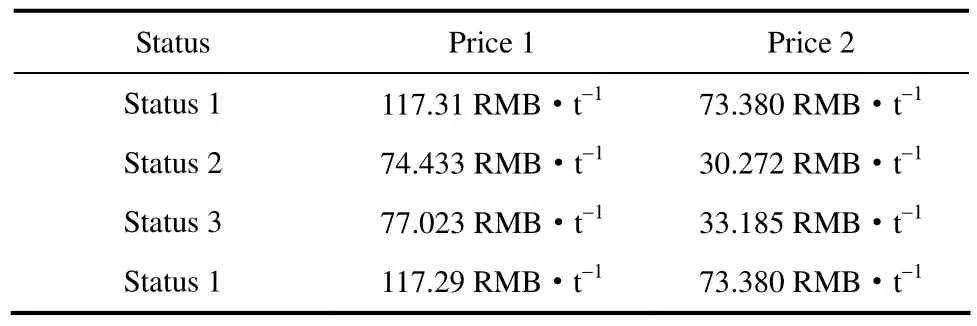
表7 经济效益优化结果Table 7 Results of economic benefit optimization

4 结 论

本文通过分析裂解炉工艺生产过程，将相关积分优化方法应用到裂解炉优化，有效地解决了裂解炉优化方法需要裂解炉具体模型以及传统优化方法的自适应性与抗干扰性不满足裂解炉优化需求的两大问题。相关积分优化方法是依据操作变量和目标函数在一段时间内的历史数据进行计算，因此不要求裂解炉在优化时生产过程处于静态，更不需要确定裂解炉生产过程的动态与静态模型。只要裂解炉优化目标函数是可以在线计算或可测量的，生产过程是连续的，就可以采用相关积分优化方法。相关积分优化方法在裂解炉优化中具有很强的自适应性与抗干扰性。

相关积分优化方法尚存在局限性。相关积分优化方法是基于梯度进行迭代计算的，若优化问题具有多个极值时，相关积分优化方法的最优解往往仅是局部最优解。此外，M、T参数的选取与实际工艺过程的时滞相关。当过程的时滞较大时，M、T须选取较大数值、建立较大的历史数据库才能保证算法的收敛性，寻找到真正的最优解。而当历史数据库较大时，则从工况变化到确定新工况的最优解需要较长时间，相关积分优化方法不能满足快速性要求。因此，相关积分优化方法的收敛性与快速性问题也有待进一步研究。

符 号 说 明

COT ——裂解炉平均出口温度

H3——副产品的产量

H4——燃料气的消耗量

H5——DS消耗量

H6——原料油消耗量

J——综合目标函数

KuJ——各操作变量与目标函数的互相关积分矩阵

kuu——操作变量自相关积分矩阵

——操作变量对综合目标函数的梯度向量

M，T——历史数据库大小参数

NP+IP——正构烷烃和异构烷烃的含量和

NP/IP——正构烷烃和异构烷烃的比例

p1，p2，p3，p4，p5，p6——分别表示乙烯、丙烯、副产品、燃料气、DS、原料油的价格

y——经济效益

σi——第i个目标函数的加权系数

0i,α——第i个操作变量的自适应步长参数初值

[1] Li Ping (李平), Li Qi’an (李奇安), Lei Rongxiao (雷荣孝),et al. Development and application of advanced process control system for ethylene cracking heaters [J].CIESC Journal(化工学报), 2011, 62 (8): 2216-2220.

[2] Wang Ling (王灵), Wang Xiuting (王秀亭), Yu Jinshou (俞金寿). Naphtha cracking furnace fault diagnosis based on adaptive quantum ant colony algorithm [J].CIESC Journal(化工学报), 2009, 60 (2): 401-408.

[3] Song Chen (宋辰), Huang Haiyan (黄海燕). Immune cultural algorithm and its applications in fault diagnosis of ethylene cracking furnace [J].CIESC Journal(化工学报), 2012, 63 (12): 3996-4002.

[4] Geng Zhiqiang (耿志强), Zhu Qunxiong (朱群雄), Gu Xiangbai (顾祥柏), Lin Xiaoyong (林晓勇). Optimal control of cracking depth based on multi-swarm competitive PSO-RBFNN for ethylene cracking furnace [J].CIESC Journal(化工学报), 2010, 61 (8): 1942-1948.

[5] Nian Xiaoyu, Wang Zhenlei, Qian Feng. A hybrid algorithm based on differential evolution and group search optimization and its application on ethylene cracking furnace [J].Chinese Journal of Chemical Engineering, 2013, 21 (5): 537-543.

[6] Shang Baopeng (商保鹏), Du Wenli (杜文莉), Jin Yangkun (金阳坤), Qian Feng (钱锋). Modeling and optimization for ethylene cracking furnace systems scheduling with consideration of changing feedstock [J].CIESC Journal(化工学报), 2013, 64 (12): 4304-4312.

[7] Sheng Jie (盛杰), Jin Yangkun (金阳坤), Li Jinlong (李进龙). Modeling and optimization of cracking process for LPG feedstock [J].Computers and Applied Chemistry(计算机与应用化学), 2013, 30 (11): 1278-1282.

[8] Zhou Shuheng (周书恒), Du Wenli (杜文莉). Modeling of ethylene cracking furnace yields based on transfer learning [J].CIESC Journal(化工学报), 2014, 65 (12): 4921-4928.

[9] Grassberger D A, Procaccia I. Measuring the strangeness of strange attractors [J].Physica D, North-Holland, Amsterdam, 1983, 9: 189-208.

[10] Takens F. Detecting strange attractors in fluent turbulence [J].Lecture Notes in Mathematics, 1981, 898: 366-381.

[11] Zhao Hong, Xia Yong, Liang Xiaoguo. Research on a diagnosis method based on a correlation integral [J].International Journal of Plant Engineering and Management, 2003, 8 (2): 65-73.

[12] Zhu Junling (朱俊玲), Lin Hong (林宏), Jiang Dazong (蒋大宗), Hu Sanjue (胡三觉). Detection of dynamic changes of pre-seizure scalp EEG with correlation integral [J].Space Medicine & Medical Engineering(航天医学与医学工程), 2004, 17 (4): 248-250.

[13] Sun Tao (孙涛), Xu Guanghua (徐光华), Zhang Sicong (张四聪), Zhang Chunmei (张春梅). Surge synptom identification of centrifugal blowers by EMD in connection with correlation integrals [J].Journal of Power Engineering(动力工程), 2006, 26 (6): 849-853.

[14] Wu Yun (吴云), Li Yinghong (李应红), Zhang Pu (张朴), Song Hui-min (宋慧敏). Correlation-integral analysis of the aerodynamic instability of an axial-flow compressor [J].Journal of Engineering for Thermal Energy and Power(热能动力工程), 2006, 21 (2): 145-149.

[15] Wang Youhong (王有红). The optimization control of petrol catalytic crack relative integral calculus based on DCS [D]. Shenyang: Northeastern University, 2006.

[16] Wang Jian (王建). A multiple input multiple output real-time continuous production process operation optimization method [P]. CN,200510085063. 2, 2006, 01.

[17] Zhang Shaoyu (张韶煜), Qiu Daiqin (邱代钦), Mu Jinyong (穆进勇). The application of DCIO in the reactor of the AE&PX united unit [J].Automation in Petro-chemical Industry(石油化工自动化), 2010, 46 (5): 20-23.

[18] Du Zhiguo (杜志国), Zeng Qingquan (曾清泉), Chen Shuo (陈硕). Progress in coking model of tube in radiation section of cracking furnace [J].Petrochemical Technology(石油化工), 2003, 32 (4): 348-352.

[19] Sadrameli S M, Green A E S. Systematics and modeling representations of naphtha thermal cracking for olefin production [J].Journal of Analytical and Applied Pyrolysis, 2005, 73 (2): 305-313.

[20] Chen Chunming (陈春明). The identification and control research of ethylene cracking furnace temperature system [D]. Harbin: Harbin Institute of Technology, 2004.

[21] Deng Rensheng (邓任生), Wei Fei (魏飞), Jin Yong (金涌). Evaluation of heavy oil pyrolysis processes according to coke treatment [J].Petrochemical Technology(石油化工), 2000, 29 (5): 364-367.

[22] Liu Shitao (刘时涛), Wang Honggang (王宏刚), Qian Feng (钱锋), Hu Guihua (胡贵华). Coupled simulation of combustion with heat transfer and cracking reaction in SL-Ⅱindustrial ethylene pyrolyzer [J].CIESC Journal(化工学报), 2011, 62 (5): 1308-1317.

Optimization of cracking furnace based on correlation integral optimal method

LIU Chunping1, WANG Xin2, WANG Zhenlei1
(1Key Laboratory of Advanced Control and Optimization for Chemical Processes,East China University of Science and Technology,Shanghai200237,China;2Center of Electrical & Electronic Technology,Shanghai Jiao Tong University,Shanghai200240,China)

Cracking furnace is the key equipment in petrochemical industry. Optimization of cracking furnace status is very important to enhance benefits of ethylene plant. Since pyrolysis reaction mechanism is complex, the model of cracking furnace is difficult to obtain and the cracking furnace has frequent disturbances, and thus it is difficult to optimize the cracking furnace status with traditional optimal methods. In order to solve the problem that the model of cracking furnace is needed in its optimization and the traditional optimal methods lack adaptivity and anti-interference, the correlation integral optimal method is proposed in this paper. First, the operating parameters affecting the benefits of cracking furnace are analyzed, the appropriate operating variables are selected and the optimal objective function is constructed. Then, the historical database is establishedviathe data of operating variables and optimal objective function. Finally, the cracking furnace status is optimized based on the iteration of correlation integral optimal method. The simulation results verify the effectiveness of the correlation integral optimal methods in cracking furnace optimization.

WANG Zhenlei, wangzhen_l@ ecust. edu. cn

10.11949/j.issn.0438-1157.20150195

TP 29

：A

：0438—1157（2015）10—4067—09

2015-02-06收到初稿，2015-06-05收到修改稿。

联系人：王振雷。

：刘春平（1991—），男，硕士研究生。

国家自然科学基金项目(U1162202)；上海市科委项目(13111103800)；上海市自然科学基金（14ZR1421800）；流程工业综合自动化国家重点实验室开放课题基金（PAL-N201404）。

Received date: 2015-02-06.

Foundation item: supported by the National Natural Science Foundation of China (U1162202), Shanghai and Municipal Science and Technology Commission (13111103800), Shanghai Natural Science Foundation (14ZR1421800), the State Key Laboratory of Synthetical Automation for Process Industries (PAL-N201404).