二元提馏式间歇精馏的优化操作与最小汽化总量

王为国，罗旌崧，曾真，王存文，吴元欣，覃远航

（1武汉工程大学化工与制药学院，湖北 武汉430074；2武汉工程大学机电工程学院，湖北 武汉430074；3武汉工程大学绿色化工过程教育部重点实验室，湖北 武汉430074）

二元提馏式间歇精馏的优化操作与最小汽化总量

王为国1，罗旌崧1，曾真2，王存文3，吴元欣3，覃远航3

（1武汉工程大学化工与制药学院，湖北 武汉430074；2武汉工程大学机电工程学院，湖北 武汉430074；3武汉工程大学绿色化工过程教育部重点实验室，湖北 武汉430074）

理想操作条件下二元提馏式间歇精馏优化操作的汽化总量与最小汽化总量的计算是约束函数优化问题。本文采用罚函数法，将此约束函数优化转变为无约束函数优化，并采用固定双步长因子梯度法数值求解该函数的极值。计算表明：固定双步长因子梯度法具有良好的收敛性，同时，降低分段数较多时，数值截断误差积累对计算结果的影响。二元提馏式间歇精馏优化操作较恒残液组成操作的能耗低的原因如下：在理论板数相对较少（接近二元提馏式间歇精馏恒残液组成操作所需的最少理论板）时，优化操作通过控制再沸比提高了能耗效率；在理论板数相对较多时，优化操作通过控制再沸比，在保证过程的能耗效率较高的同时，可尽可能快地将物料移出系统，减少了精馏过程中塔顶贮槽内液体的混合熵产。通过对计算结果的归纳与外推，得到了理想操作条件下理论板数为无穷多时二元提馏式间歇精馏优化操作再沸比的变化方式以及最小汽化总量的计算公式。

提馏式间歇精馏；优化操作；汽化总量；模拟；能耗

引 言

间歇精馏是经常用于小规模生产的一个重要的单元操作。间歇精馏分离二元混合物，根据出料方式，具有代表意义的操作方法有常规间歇精馏（主要特征：间歇精馏过程中塔顶连续出料、塔底存料，精馏终了塔底集中出料）、塔顶累积全回流间歇精馏（主要特征：间歇精馏过程中塔顶、塔底均存料，精馏终了塔顶、塔底集中出料）与提馏式间歇精馏（主要特征：间歇精馏过程中塔顶存料，塔底连续出料，精馏终了塔顶集中出料）等[1]。间歇精馏提馏式操作方法最早由Robinson和Gilliland[2]于1950年提出。Hasebe等[3]及Mujtaba等[4-5]都对提馏式间歇精馏塔进行了不同程度的研究。Chiotti等[6-7]针对二元物系的间歇精馏过程分别建立了基于亚稳态过程的提馏式间歇精馏塔和精馏式间歇精馏塔的数学模型。通过模拟研究发现，与常规间歇精馏相比，在分离原料中含有大量难挥发组分的精馏过程中，提馏式间歇精馏塔更加经济适用。Sorensen等[8]对常规间歇精馏塔和提馏间歇精馏塔的动态特性及最优操作时的能耗进行了比较，得到当原料中轻组分含量很低的时候,使用提馏式间歇精馏操作明显优于常规间歇精馏操作。许松林等[9-10]对提馏式间歇精馏塔的设计方法及控制方法进行了研究。张雪梅等[11]对二元恒再沸比提馏式间歇精馏过程的最小再沸比进行了理论推导。近来作者对间歇精馏基础理论进行了研究[12-20]，文献[19]将提馏式间歇精馏分为恒再沸比与恒残液组成两种典型操作, 完善了二元恒再沸比提馏式间歇精馏最小再沸比计算方法，推导出二元提馏式间歇精馏恒残液组成操作，在理想操作条件下的最小汽化总量的计算公式,分析了二元提馏式间歇精馏，相对于恒残液组成操作，要求残液中重组分的收率高和轻组平均浓度低时，采用恒再沸比操作能耗较高的原因。文献[20]由理想操作条件下，恒残液组成提馏式间歇精馏二元理想混合物，理论板数与汽化总量对应关系的数值计算结果，关联出理论板数与汽化总量的近似关系式（捷算法）。文献[13]采用罚函数法，将理想操作条件下二元常规间歇精馏优化操作的汽化总量与最小汽化总量转变为无约束函数优化求解，并采用固定单步长因子梯度法数值求解该函数的极值，在分段数较多时，优化操作的汽化总量与最小汽化总量取不同方法赋回流比初值的收敛结果中最小者。明显这种有限穷举赋回流比初值方法获得计算结果，在许多情况下，与其真数值解有较大的偏差。本文以过程能耗最小为目标，采用罚函数法，将理想操作条件下二元提馏式间歇精馏优化操作的汽化总量与最小汽化总量转变为无约束函数优化求解，研究函数优化求解的数值计算方法，并由数值计算结果对过程能耗进行分析，最后，由理想操作条件下理论板数为无穷多时二元提馏式间歇精馏优化操作的数值计算结果，归纳与外推二元提馏式间歇精馏优化操作的再沸比变化方式以及最小汽化总量计算公式。

1 二元提馏式间歇精馏优化操作的数值计算方法

1.1 数值计算方法

二元提馏式间歇精馏流程、操作条件及基本方程均同文献[19]，本文所谓优化操作是指对于给定的分离任务，通过控制过程再沸比，使塔釜汽化总量达到最小。二元提馏式间歇精馏一批料的塔釜汽化总量

对于给定的分离任务和理论板数，采用提馏式间歇精馏求优化操作时的汽化总量nVT,opt，在数学上是约束函数优化问题。用罚函数法将其转化成无约束函数优化，其表达式为

式中，μ为罚因子（正常数）。

1.1.1 工作方程 将塔顶贮槽内液体中轻组分浓度xD由xF变为xDe的精馏过程进行等距离散，取离散段数为k，则

式（11）中，ωin与ωout为步长因子（小正数）。

1.1.2 计算步骤N+1为有限时，采用固定双步长因子梯度法求解Rb,i,opt（i=1,2,…,k）与nVT,opt的具体步骤如下：

（1）输入：α、nF、xF、ηh、xWm、N+1、k、ωin和ωout。

（2）计算nWe、nDe、xDe、ΔxD和xD,i（i=0,1,2,…,k）。

（3）s=0，ss=0，赋初值。

（10）计算nVT,opt（由式（1）得，判断是否达到收敛要求

①如果达不到，转到（11）；

②如果达到，转到（12）。

（12）输出计算结果。

对于采用上述步骤编程时，补充说明如下：

计算实践显示，在本文实例计算时，δ较为适合取值为δ=0.0001。理论上δ取值愈小，计算出愈接近真值，但δ取值过小（如δ=0.00001），数值截断误差相对较大，导致的计算结果不稳定。

（3）离散段数k的取值。理论上k取值愈大，计算结果愈接近真值，但计算量愈大。对于本文分离任务（α=2.5、Fx=0.5、Wmx=0.06和hη=0.9，在后文中所说的本文分离任务均指此分离任务），由图17可见，在N+1→∞与k=100时，数值计算结果nVT,min,opt/nF=2.0435，由式（31）得到解析计算结果nVT,min,opt/nF=2.0430，两者相对偏差为0.0245%。说明分段数k=100时，对于本文分离任务，数值计算已有较好的精度，因此，如果不做特殊说明，后文所有计算结果均是在k=100条件下算出。

（4）罚因子μ的取值与收敛判据。对于本文分离任务，由构造的罚函数[式（2）]，数值计算结果中约束条件最小残差，为了计算结果尽可能符合约束条件，后文所有计算均取μ=107。

采用固定双步长因此梯度法求解nVT,opt的计算程序是由两循环构成，因此，收敛判据有两个，分别称之为内循环判据与终点判据。由于内循环是对Rb,i（i=1,2,…,k）进行满足约束条件的迭代修正，因此，为了使内循环收敛结果尽可能符合约束条件，内循环判据直接为约束条件的残差，或者经多次内循环，如果多次迭代不满足上述收敛判据，表明ωin取值过大。终点判据即判断nVT是否收敛至nVT,opt，本文未能很好地解决，计算终点判断有较强主观性。当nVT收敛至nVT,opt后，再进行迭代计算，计算出的nVT应不变，因此，终点判据为：计算出的nVT在一较小范围内振荡。由于本文计算过程愈近终点，收敛速度愈慢，在接近终点时，会出现nVT,在较小范围内振荡接近nVT,opt，这为终点判断带来偏差。对本文分离任务，ωin与ωout选取适宜条件下，当Rb,i=Rb,i,opt（i=1,2,…,k）时，内循环的(∂F/∂Rb,i)s,ss呈现近似周期性变化，最显著特征是(∂F/∂Rb,1)s,ss≈ (∂F/∂Rb,1)s,s+1。以此作为辅助终了判据，可减少主观判断的偏差。

1.2 固定双步长因子梯度法的提出与验证

梯度法]22[，又称最速下降法，是一种求解无约束多元函数极值的数值方法，具有良好的收敛性。本文采用罚函数法，将求解理想操作条件下，二元提馏式间歇精馏优化操作的汽化总量nVT,opt与最小汽化总量nVT,min,opt转变求解无约束函数极值。本文首先采用固定单步长因子梯度法迭代求解本文分离任务的nVT,opt。在理论板数相对较少时（接近恒残液组成提馏式间歇精馏所需的最少理论板），选取适宜的步长因子，可收敛至稳定结果。对于本文分离任务，二元提馏式间歇精馏恒残液组成操作所需的最少理论板为6.45。图1为N+1=7与k=100时，采用固定单步长因子梯度法数值求解本文分离任务nVT,opt的收敛过程与结果。由图1可见。在计算终点，三者的|ωs(∂F/∂Rb,i)/Rb,i|＜10−7（i=1,2,…,k），因此，采用固定单步长因子梯度法，nVT,opt最终收敛结果受数值截断误差积累影响，ωs取值愈小，数值截断误差积累对计算结果影响愈大。当ωs=0.004时，在迭代230万次后，nVT,opt/nF在4.446875～ 4.448421范围内波动，在 10−6～10−5范围内波动。即采用固定单步长因子梯度法数值求解，ωs取值过大，不能得到稳定的收敛结果。此外，图4中ωin,c也是固定单步长因子梯度法度法迭代求解nVT,opt，使Rb,i（i=1,2,…,k）收敛到满足约束条件（收敛精度为10−7）的ωs最大取值（N+1=7，ωin,c≈0.0031）。

图1 固定单步长因子梯度法的收敛过程（N+1=7）Fig.1 Convergence process of fixed single step length factor gradient method (N+1=7)

对于本文分离任务，N+1较多时（N+1≥12），采用固定单步长因子梯度法迭代求解nVT,opt得到：在k=100与步长因子取值满足计算过程收敛条件下，如果给定的Rb,i（i=1,2,…,k）初值满足约束条件（如：以二元提馏式间歇精馏恒残液组成操作的计算结果为初值），出现了“初值即结果”现象，如果给定的初值不满足约束条件，出现了“初值决定结果”现象。采用精确线性搜索最优步长因子梯度法迭代求解nVT,opt，也得到类似的现象。

对于本文分离任务，采用固定单步长因子梯度法迭代求解nVT,opt，计算结果显示，在N+1较多（N+1≥12）、k=100与步长因子取值满足计算过程收敛条件下，nVT收敛至稳定结果时，|ωs(∂F/∂Rb,i)/Rb,i|（i=1,2,…,k）中绝大部分的数值小于10−7，只极少部分（或没有）的数值在一定范围内振荡。再根据采用固定双步长因子梯度法迭代求解的本文分离任务的nVT,opt结果，本文认为N+1较多时（对于本文分离任务，N+1≥12），采用固定单步长因子梯度法迭代求解nVT,opt，出现了“初值即结果”或“初值决定结果”现象原因为：在离散段数较多时，Rb,1,opt与Rb,2,opt不呈渐变[参见图8（c）与（d）]。在接近收敛结果时，|∂F/∂Rb,1|≫|∂F/∂Rb,i|（i=1,2,…,k）（参见图2），相对较大|∂F/∂Rb,1|使Rb,i（i=1,2,…,k）收敛到满足约束条件（收敛精度为10−7）的步长因子允许取值较小（参见图4中ωin,c）。而步长因子取值较小时，数值截断误差积累对计算结果影响较大。

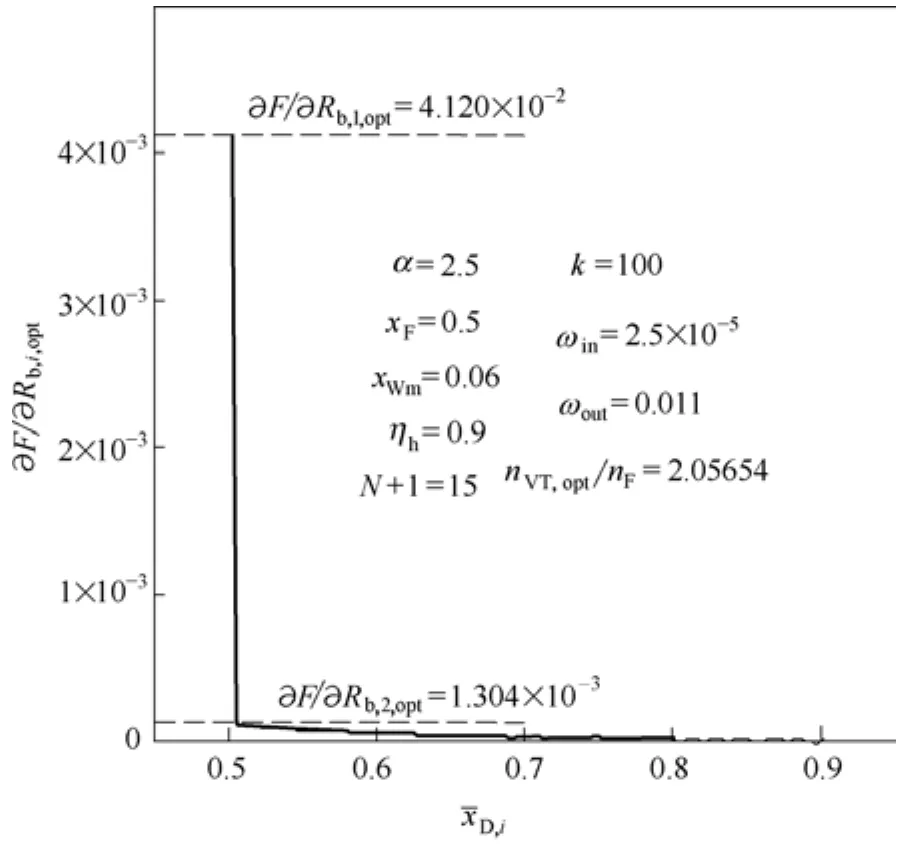
图2 优化操作时∂F/∂Rb,i,opt随D,i的变化（N+1=15）Fig.2 Changing of ∂F/∂Rb,i,optwithD,iunder optimal operation (N+1=15)

对于本文分离任务，采用精确线性搜索法确定最优步长因子的梯度法迭代求解nVT,opt，计算结果显示，在满足约束条件后，再继续迭代，Rb,i与nVT不再变化。此时，精确线性搜索法确定的最优步长因子近似为0。由式（7）可见，∂F/∂Rb,i由两部分构成，其一为汽化总量贡献，记为Ai，其二为约束条件贡献，记为。图3表示的采用固定双步长因子梯度法，以二元提馏式间歇精馏恒残液组成操作的计算结果，Rb,i（i=1,2,…,k）为初值，编程计算本文分离任务的nVT,opt,在数值计算的起始与终了时，Ai与Ci的变化。图3中，线1、2分别表示在数值计算的起始与终了时，Ai的数值（点，A1=0.29435未在线2中示出），线3、4分别表示在数值计算的起始与终了时，Ci的数值（点，C1=0.28314未在线4中示出）。由图3可见，Ai与Ci在计算过程中变化很小且很接近，因此，本文认为|B|变化是引起∂F/∂Rb,i变化的主要因素，对不满足约束条件的Rb,i（i=1,2,…,k），由于|B|较大，B×Ci在∂F/∂Rb,i占比例较大，梯度法迭代修正Rb,i（i=1,2,…,k）时，B×Ci起作用较大，即：梯度法迭代修正Rb,（ii=1,2,…,k）优先满足约束条件。采用精确线性搜索法确定最优步长因子的梯度法，线性搜索的目标是||∂F/∂Rb,i||达到最小，对满足约束条件的Rb,i（i=1,2,…,k）进行修正，如果步长因子不为0，修正后必然会使其不再满足约束条件，|∂F/∂Rb,i|会大幅增大，因此，在满足约束条件后，再继续迭代，精确线性搜索法确定的最优步长因子近似为0。

图3 数值计算过程中Ai与Ci的变化（N+1=15）Fig.3 Changing ofAiand Ciin process of numerical calculation (N+1=15)

由N+1=7与k=100时，采用固定单步长因子梯度法数值求解本文分离任务nVT,opt的收敛结果（参见图1）可知，，即：采用固定单步长因子梯度法，ωs取值愈大，数值截断误差积累对计算结果影响愈小。为了解决采用固定单步长因子梯度法迭代求解nVT,opt，离散段数较多时，步长因子取值满足Rb,i（i=1,2,…,k）可收敛至约束条件，收敛到的稳定结果，在许多情况下，由于数值截断误差积累对计算结果影响较大，数值计算结果与真数值解有较大的偏差；而步长因子取值较大，数值计算过程不收敛的矛盾，本文提出一迭代求解nVT,opt的计算方法，具体计算过程为：先采用较小步因子长的梯度法对Rb,i（i=1,2,…,k）进行迭代修正，当Rb,i（i=1,2,…,k）满足约束条件后，再采用较大步长因子的梯度法对Rb,i（i=1,2,…,k）进行修正一次，再转入Rb,i（i=1,2,…,k）满足约束条件的小步因子长梯度法迭代修正，此过程重复进行（详见1.1.2节），本文称此计算方法为固定双步长因子梯度法。

对于本文分离任务，17N+=时，采用固定双步长因子梯度法求解nVT,opt的最终结果为：，较采用固定单步长因子梯度法计出的最小略小，其原因为：采用固定双步长因子梯度法的进行数值计算时，ωout可取较大数值，在计算终点，|ωout(∂F/∂Rb,i)/Rb,i|（i=1,2,…,k）中绝大部分的数值大于10−6，即：在迭代过程中，外循环的修正量ωout(∂F/∂Rb,i) （i=1,2,…,k）始终对Rb,i（i=1,2,…,k）起到修正作用。因此，固定双步长因子梯度法，ωout可取较大数值，有效降低了数值截断误差积累对计算结果影响，数值计算结果与实际的偏差更小。采用固定双步长因子梯度法求解nVT,opt，计算结果显示，对本文分离任务，Rb,i（i=1,2,…,k）初值适宜，ωin与ωout取值合理，均可计算出合理的结果。

1.3 实例的数值计算结果与讨论

1.3.1 内循环步长因子的取值 采用固定双步长因子梯度法编程计算本文分离任务的Rb,i,opt（i=1,2,…,k）与nVT,opt，ωin对内循环的次数有较大的影响。图4中虚线ωin,c是采用收敛结果Rb,i,opt（i=1,2,…,k）的反算出来，主观性较强，由收敛结果Rb,i,opt（i=1,2,…,k）经一次外循环后，保证程序内循环收敛的最大步长因子。在Rb,i（i=1,2,…,k）接近Rb,i,opt（i=1,2,…,k）与ωin=(0.4～0.6)ωin,c时，数次内循环即可满足约束条件。图4中实线为本文举例计算过程中内循环步长因子ωin实际取值，ωin≈0.5ωin,c。此外，当Rb,i（i=1,2,…,k）与Rb,i,opt（i=1,2,…,k）差别较大时，取ωin≈0.5ωin,c，每一次外循环后，要再收敛至满足约束条件，需内循环次数较多。如N+1=15时，以恒残液组成操作的计算结果为初值，ωout=0.011和ωin=0.000025时，计算起始时，每一次外循环后，要再收敛至满足约束条件，需经300余次内循环。

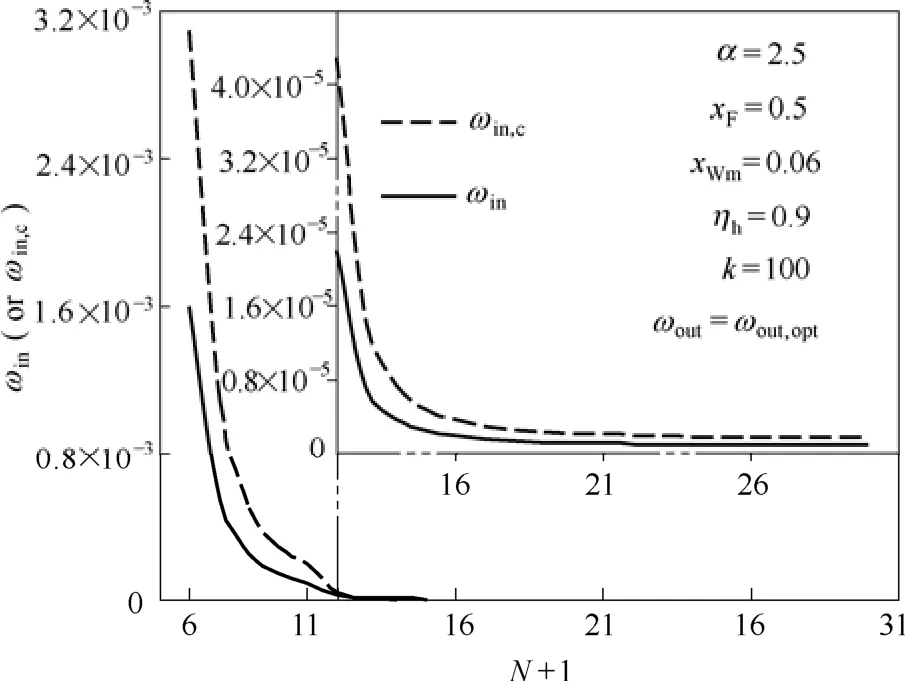
图4ωin与N+1的关系Fig.4 Relationship betweenωinandN+1

1.3.2 再沸比的初值对计算结果的影响 采用固定双步长因子梯度法编程计算本文分离任务的Rb,i,opt（i=1,2,…,k）与nVT,opt，计算结果显示，当N+1≤12时，计算结果仅受ωout影响，而当N+1≥13时Rb,i（i=1,2,…,k）初值对计算结果有细微的影响，以1N+=15为例：

①以N+1=14时计算出的为初值、ωout=0.011和ωin=0.000025时，外循环10余万次，计算出的nVT,opt/nF=2.056478；

②以N+1=16时计算出的为初值、ωout=0.011和ωin=0.000025时，外循环10余万次，计算出的nVT,opt/nF=2.056417；

④以Rb,1=0.1Rbmc,1，Rb,i=Rbmc,i（i=1,2,…,k）（Rbmc用本式（25）计算）为初值，ωout=0.011和ωin=0.000025外循环10万余次，计算出的nVT,opt/nF=2.056405。

四者的nVT,opt差别出现在小数点后第5位，最大相对偏差为0.005%。由此可见：采用固定双步长因子梯度法编程计算本文分离任务的Rb,i,opt（i=1,2,…,k）与nVT,opt，ωin与ωout取值合理时,初值对计算结果影响可忽略，但影响计算工作量。此外，在计算终点，四者的内循环均呈现近似周期性变化，因此，本文认为四者的偏差是由计算过程中数值截断误差积累引起的，即：采用固定双步长因子梯度法编程计算本文分离任务的Rb,i,opt（i=1,2,…,k）与nVT,opt，可降低分段数较多时，数值截断误差积累对计算结果的影响，但不能完全消除。

1.3.3 外循环步长因子取值 图5中ωout是采用固定双步长因子梯度法编程计算本文分离任务的Rb,i,opt（i=1,2,…,k）与nVT,opt的外循环步长因子取值。外循环步长因子取值在(1±0.5)ωout范围内，计算出的nVT,opt/nF数值差异为±10−6，ωout取值超出2ωout时，未观察到计算终点的近似周期性，当N+1≥13时, 外循环步长因子取值超出5ωout时，直接以Rb,i,opt（i=1,2,…,k）为初值，计算过程明显发散。1.3.4 实例的数值计算结果 对于本文分离任务，采用固定双步长因子梯度法的计算结果见图6～图8。图6为数值计算出随N+1变化，由图6可见，优化操作的能耗均低于恒残液组成操作，其原因将在本文第2节讨论。

图5ωout与N+1的关系Fig.5 Relationship betweenωoutandN+1

图6 优化操作与恒残液组成操作的汽化总量Fig.6 Total evaporation of optimize operation and constant residual fraction composition operation

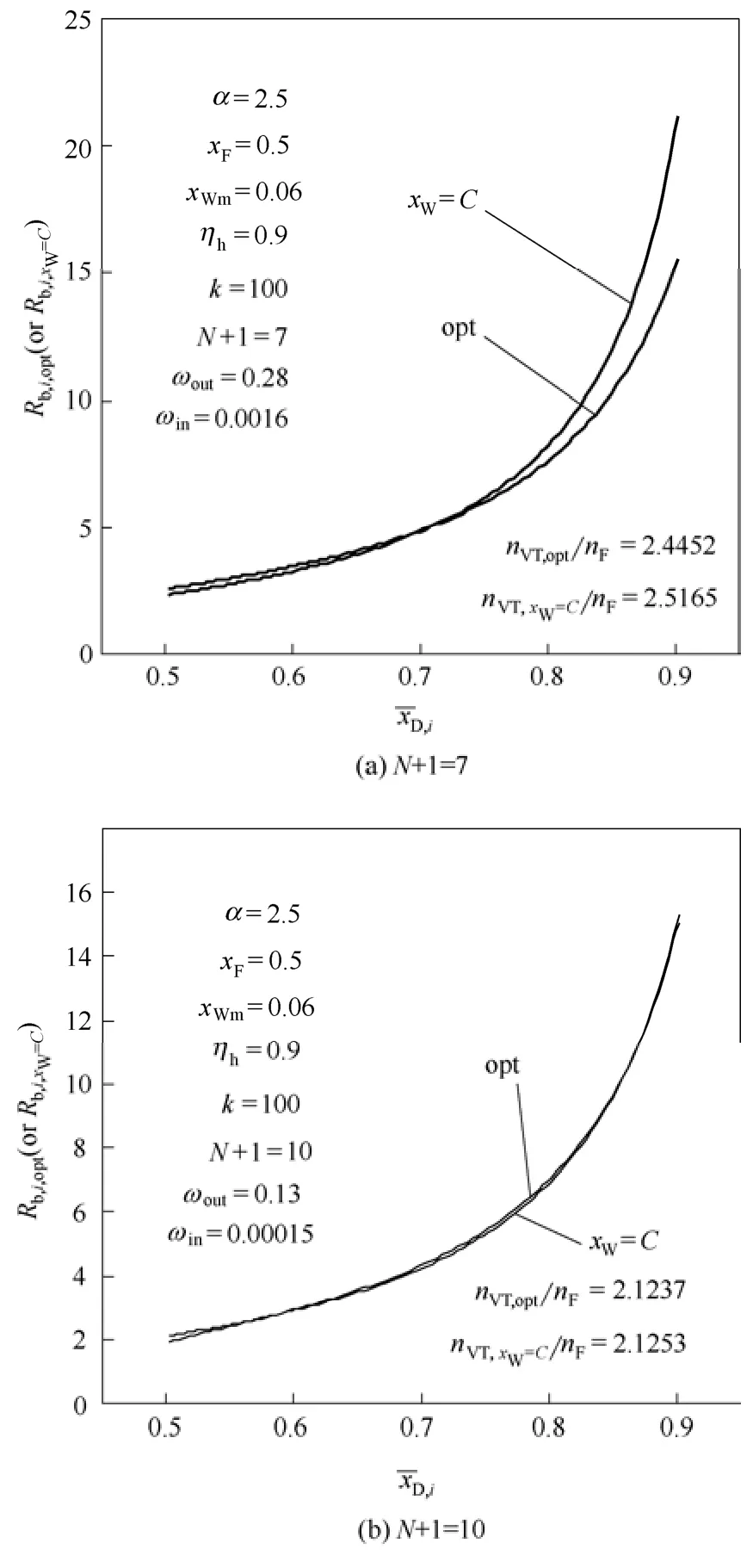
图7（a）～（d）分别为理论板数7、10、12和20块时，优化操作及恒残液组成操作再沸比的变化规律。由图6可见，优化操作与恒残液组成操作的再沸比均随着xD的增大而增大。由图7（c）、（d）可见，理论板数较大时，优化操作的再沸比，在起始阶段不呈渐变。

图7N+1对Rb,i,opt随变化规律的影响Fig.7 Effect ofN+1 on rule ofRb,i,optwith change of

图8W,i,opt（i=1,2,…,k）随N+1的变化规律Fig.8 Rule ofW,i,opt(i=1,2,…,k) with change ofN+1

2 二元提馏式间歇精馏优化操作的能耗分析

由图6可见,优化操作的能耗均低于恒残液组成操作，下文将对其原因进行分析。图9表示随N+1的变化规律，数据来源于图6，由图9可见，存在极小值，表明至少有两个因素对其有影响，下文从精馏过程中的能耗效率与塔顶贮槽内液体的混合熵产两方面进行讨论。

2.1 能耗效率的计算方法与结果

文献[19]提出

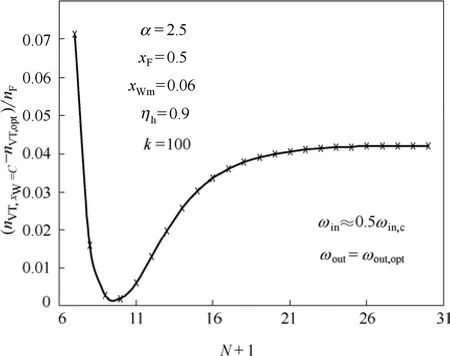
图9(nVT,xW=C−nVT,opt)nF随N+1的变化规律Fig.9 Rule of (nVT,xW=C−nVT,opt)nFwith change ofN+1

用φ数值大小的表示其对应的能耗对分离效果的影响程度，0≤φ≤1，对应φ值较小的这一部分能耗为低效能耗，本文直接称φ为能耗效率。总平均能耗效率φt为能耗效率对总能耗平均，由式（1）得

将式（14）离散得

式（15）中，φa,i为第i段的平均能耗效率，第i段的再沸比为Rb,i，此段的能耗中能包括0＜Rb＜Rb,i所对应的能耗, 由文献[19]图5可见，φ随Rb变化，因此，第i段的平均能耗效率为Rb在区间{0，Rb,i}内对应能耗效率平均，即

式（13）代入式（16）积分整理得

对给定分离任务，φt的计算方法为：先将过程离散进行数值计算，应用其计算结果，由式（17）计算出第i段的φa,i（i=1,2,…,k），再式（15）计算出φt。本文分离任务φt的计算结果见图10，计算φt所需的变量数值源于获得图6的计算结果。

图10φt随N+1的变化规律Fig.10 Rule ofφtwith change ofN+1

2.2 塔顶贮槽内液体混合熵产的计算方法与结果

混合是分离的逆过程，二元提馏式间歇精馏过程中，塔顶贮槽内不同浓度液体混合必然有熵产，减少塔顶贮槽内液体的混合熵产意味着降低过程能耗。对塔顶贮槽内液体混合熵衡算得：

式（18）中

将式（19）、式（20）离散得

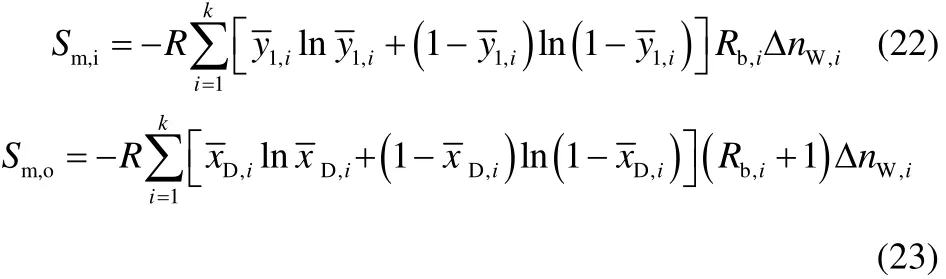
对给定分离任务，塔顶贮槽内流动液体混合熵产Sm,p的计算方法为：先将过程离散进行数值计算，应用其计算结果，由式（23）、式（22）与式（21）分别计算流出系统混合熵Sm,o、流入系统混合熵Sm,i与系统混合熵积累Sm,a，再通过式（18）计算出系统混合熵产Sm,p。对于本文分离任务，Sm,p的计算结果见图11，计算Sm,p所需的变量数值源于获得图6的计算结果。

图11Sm,p/nF的随N+1的变化规律Fig.11 Rule ofSm,p/nFwith change ofN+1

2.3 优化操作的能耗分析

图12中nW,1,opt/nF源于获得图6的计算结果，表示优化操作时第1段的塔底出料量nW,1,opt/nF与N+1的关系。由图12可见，nW,1,opt/nF随N+1的增大而增加，由图11可见，Sm,p/nF随N+1的增大而减小。因此，本文认为，二元提馏式间歇精馏优化操作，N+1较多时，精馏起始阶段出料量较大，减小过程后期的塔顶贮槽的存液量，从而减小塔顶贮槽内液体的混合熵产。

图12 ΔnW,1,opt/nF随N+1的变化规律Fig.12 Rule of ΔnW,1,opt/nFwith change ofN+1

结合图10～图12可得，对于本文分离任务，N+1=7,8时，。再由图7（a）可见，优化操作的Rb与恒残液组成操作有明显差异。因此，在理论板数相对较少时，二元提馏式间歇精馏优化操作的能耗较恒残液组成操作低的原因是优化操作通过控制再沸比，提高过程的能耗效率。N+1≥ 12时，但均接近1，。因此，在理论板数相对较多时，二元提馏式间歇精馏优化操作的能耗较恒残液组成操作低的原因是优化操作通过控制再沸比，在保证过程的能耗效率较高前提下，尽可能快地将物料移出系统，减少了过程中塔顶贮槽内液体的混合熵产。此外，N+1=10时，。再由图7（b）可见，优化操作与恒残液组成操作的Rb,i（i=1,2,…,k）差异很小，因此，两者能耗差达到最小。

3 优化操作最小汽化总量的数值计算方法与解析计算方法

对于给定的分离任务，在理想操作条件下，二元提馏式间歇精馏优化操作，N+1→∞，nVT,opt→nVT,min,opt。

3.1 最小汽化总量的数值计算方法

由文献[19]图4可见，N+1→∞时，塔底残液中轻组分瞬时浓度与塔顶贮槽液体中轻组分的瞬时浓度及再沸比之间的关系可表达成为

式（24）中，Rbmc为N+1→∞时塔顶和塔底同时为恒浓区的再沸比，由文献[19]知

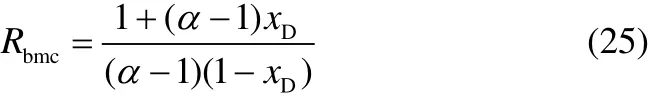
由式（24）得

将1.1节所介绍的nVT,opt计算过程中，步骤（4）的计算方法，取塔顶贮槽液体中轻组分平均浓度，改用式（24）计算；步骤（6）用数值微分法计算（i=1,2,…,k），取塔顶贮槽液体中轻组分平均浓度，改用式（26）计算，即可得到最小汽化总量的数值计算方法。

采上述方法编程对本文分离任务的nVT,min,opt/nF进行计算。Rb,i,min（i=1,2,…,k）的初值对计算结果有细微的影响，k=100、ωin=10−6与ωout=0.001时，Rb,i,min（i=1,2,…,k）初值不同，nVT,min,opt/nF计算结果在2.043471～2.0434786内波动，本文取nVT,min,opt/nF=2.0435是本文分离任务优化操作时所需的最小汽化总量。

图13中，实线表示N+1与nVT,opt/nF的关系，数据同图6，虚线是N+1→∞时，nVT,min,opt/nF的数值计算结果。由图13可见，随N+1增大，nVT,opt/nF的nVT,min,opt与直接数值计算出的nVT,min,opt是相同的。

图13nVT,min,opt/nF与nVT,opt/nF的比较Fig13 Comparison ofnVT,min,opt/nFwithnVT,opt/nF向nVT,min,opt/nF趋近，表明nVT,opt的计算结果外推出

3.2 最小汽化总量的解析计算方法

由式（1）可见，要得到nVT,min,opt的计算公式，必须得到N+1→∞时精馏过程的Rb,min,opt变化规律。由图14可见，除第一点Rb,min,1,opt外，数值计算出的Rb,min,i,opt与Rbmc,i是重合的，直接对两者数值进行比较得到|Rb,min,i,opt−Rbmc,i|＜10−5。的数值计算在0～10−6范围内波动，结合图8的（i=1,2,…,k）随N+1的变化趋势可得：二元提馏式间歇精馏优化操作，N+1→ ∞时，除起始阶段，Rb,min,opt=Rbmc，xW,opt=0 。

图14N+1→∞时Rb,min,i,opt与关系Fig.14 Relationship betweenRb,min,i,optandunderN+1→∞

图15、图16表示过程的离散段数k对Rb,min,1,opt与的影响，由图15可见，随着分段数的增加，Rb,min,1,opt向0趋近，即：，由图16可见，随着分段数的增加，向xF趋近。即：。由此可得：二元提馏式间歇精馏优化操作，N+1→∞时，起始阶段，Rb,min,opt=0，xW,opt=xF。

综上所述，N+1→∞时，二元提馏式间歇精馏优化操作，Rb,min,opt的变化方式为由起始Rb,min,opt=0（xW,opt=xF）突变为Rb,min,opt=Rbmc（xW,opt=0），并保持到过程结束。用nWC表示精馏起始至突变点前的釜底出料量，Rb,min,opt的变化方式可表达为

式（27）代入式（1）得

图15k对Rb,min,1,opt计算结果的影响Fig.15 Effect ofkon numerical results ofRb,min,1,opt

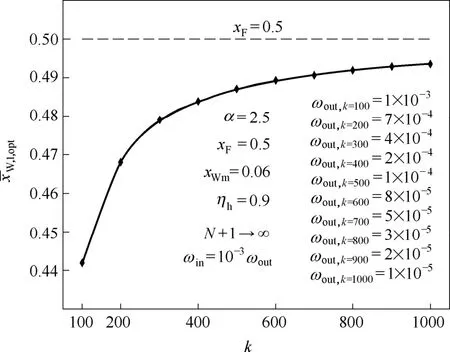
图16k对W,1,opt计算结果的影响Fig.16 Effect ofkon numerical results ofW,1,opt

二元提馏式间歇精馏优化操作，塔底出料量由0到nWC精馏过程中，xW,opt=xF；釜底出料量由nWC到nWe精馏过程中，xW,opt=0。对轻组分物料衡算得

将式（30）微分得

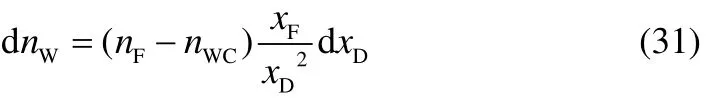
将式（29）与式（31）代入式（28）积分整理得

对于本文分离任务，由式（29）计算得：nWC/nF= 0.0574，由式（32）计算得：nVT,min,opt/nF=2.0430。

图17中，实线表示数值计算结果nVT,min,opt/nF与离散段数k关系，虚线表示nVT,min,opt/nF的解析计算结果。由图17可见，随k增大，数值计算结果向解析计算结果趋近，表明由不同离散段数数值计算结果外推出的nVT,min,opt/nF与解析计算结果是相同的。

图17k对nVT,min,opt/nF计算结果的影响Fig.17 Effect ofkon numerical results ofnVT,min,opt/nF

3.3 最小汽化总量的解析计算方法的合理性说明

由数值计算结果归纳出nVT,min,opt解析计算方法的合理性需用数学分析法证明，本文未能完成。下文通过对给定分离任务的nVT,min,opt和解析计算结果比较及热力学分析，对nVT,min,opt解析计算方法的合理性进行说明。

表1中9个分离任务是理想操作条件下，常用范围内，对确定二元提馏式间歇精馏分离任务的4个独立变量（α,xF,xWm,ηh）采用3水平正交设计方案取值拟给定的，二元恒残液组成提馏式间歇精馏的塔釜最小汽化总量nVT,min,xD=CnF按文献[19]式（25）计算。由表1可见，对于所有的分离任务nVT,min,opt/nF均小于nVT,min,xD=CnF，因此，从具体分离任务计算结果看，nVT,min,opt解析计算方法是合理的。

由图12可见，ΔnW,1,opt/nF随N+1的增大而增加，并向ΔnW,1,opt,N+1→∞/nF趋近，即：对本文分离任务，k=100时，ΔnW,1,opt,max/nF=ΔnW,1,opt,N+1→∞/nF= 0.0650。对于本文分离任务，由式（29）得：nWC/nF=0.0574。由图18可见，随着分段数增大，ΔnW,1,opt,N+1→∞/nF向nWC/nF=0.0574趋近，即，nWC/nF=0.0574是优化操作时起始阶段最大出料量，结合图10、图11可得，此时，塔顶贮槽内液体的混合熵产达最小。

图18k对ΔnW,1,opt,N+1→∞/nF计算结果的影响Fig.18 Effect ofkon numerical results of ΔnW,1,opt,N+1→∞/nF

综上所述，归纳与外推得到，N+1→∞时，在理想操作条件下，二元提馏式间歇精馏优化操作，Rb,min,opt的变化方式由起始Rb,min,opt=0（xW,opt=xF）突变为Rb,min,opt=Rbmc（xW,opt=0），并保持到过程结束，实现了过程能耗效率（φt=1）最高，塔顶贮槽内液体的混合熵产最小，即过程能耗最小。因此，从热力学上说，nVT,min,opt解析计算方法是合理的。

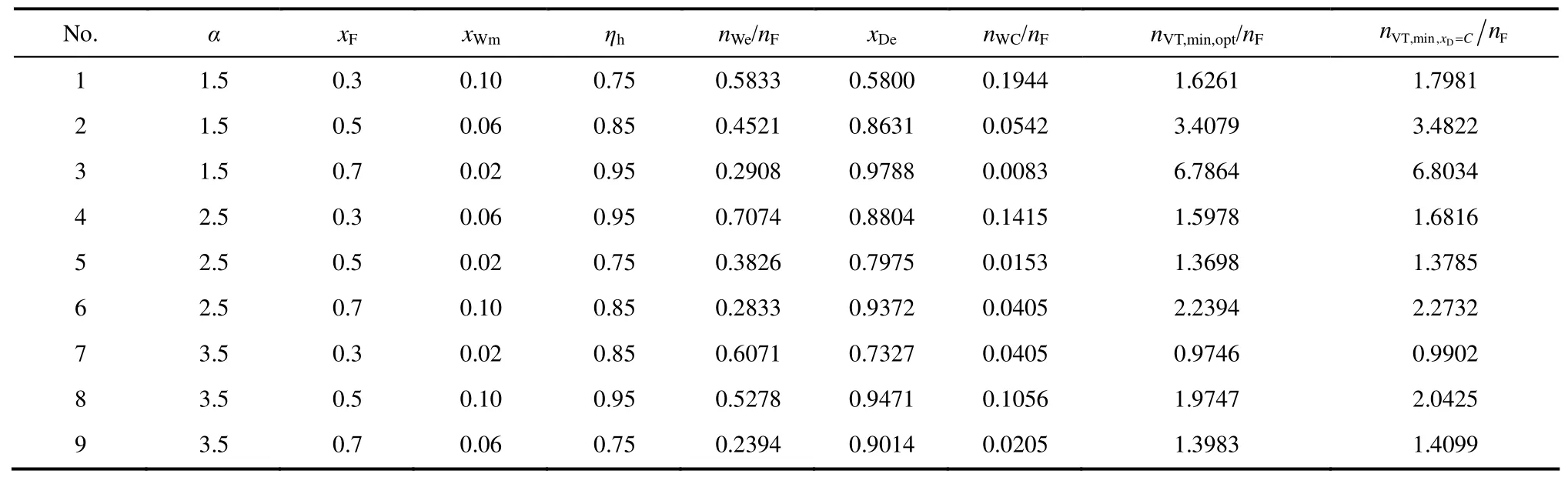
表1nVT,min,opt/nF和nVT,min,xD=C解析计算结果的比较Table 1 Analytical results ofnVT,min,opt/nFcompared withnVT,min,xD=C

4 结 论

（1）采用罚函数法，将求解理想操作条件下，二元提馏式间歇精馏优化操作的汽化总量与最小汽化总量转变求解无约束函数极值。通分析该函数的结构与具体计算数据，设计一数值法求解极值的计算过程，先采用较小步因子长的梯度法对Rb,i,(i=1,2,…,k)进行迭代修正，当Rb,i,(i=1,2,…,k)满足约束条件后，再采用较大步长因子的梯度法对Rb,i,(i=1,2,…,k)进行修正一次，再转入Rb,i,(i=1,2,…,k)满足约束条件的小步因子长梯度法迭代修正，此过程重复进行（本文称之为固定双步因子长梯度法）。模拟的计算实践显示，固定双步长因子梯度法求解二元提馏式间歇精馏优化操作的nVT,opt与nVT,min,opt具有良好的收敛性，同时，降低分段数较多时，数值截断误差积累对计算结果的影响。

（2）由模拟计算结果对过程能耗分析得到提馏式间歇精馏优化操作的能耗较恒残液组成操作低的原因。在理论板数相对较少（接近恒残液组成提馏式间歇精馏所需的最少理论板）时，优化操作通过控制过程再沸比，提高了过程的能耗效率；在理论板数相对较多时，优化操作通过控制过程再沸比，保证过程的能耗效率较高同时，尽可能快地将物料移出系统，减少了过程中塔顶贮槽内液体的混合熵产。

（3）由模拟计算结果归纳与外推得到，N+1→∞时，在理想操作条件下，二元提馏式间歇精馏优化操作再沸比的变化方式。Rb,min,opt变化方式为由起

始Rb,min,opt=0（xW,opt=xF）突变为Rb,min,opt=Rbmc

（xW,opt=0），并保持到过程结束。由Rb,min,opt的此变化方式推导出最小汽化总量的计算公式。Rb,min,opt的此变化方式，实现了过程能耗效率（φt=1）最高，塔顶贮槽内液体的混合熵产最小，即过程能耗最小。

符 号 说 明

k——数值计算时，全过程离散的段数

N+1 ——理论板数（包括塔釜）

nD、nF、nDe——分别为塔顶贮槽中瞬时存液量、原料量与塔顶产品量，kmol

nVT——精馏一批料的汽化总量，kmol

nW、nWe——分别为精馏起始至某瞬时塔底出料液总量与塔底产品量，kmol

nWC——N+1→∞时，起始Rb,min,opt=0的塔底出料液总量，kmol

ΔnW,i、ΔnV,i——精馏过程第i段塔底出料液总量与汽化量，kmol

R——通用气体常数，R=8.314472 kJ·K−1·kmol−1

Rb——再沸比

Rbmc——N+1→∞时,塔顶和塔底同时为恒浓区的再沸比

Sm,a、Sm,i、Sm,o、Sm,p——分别为塔顶贮槽内液体混合熵积累、流入塔顶贮槽混合熵、流出塔顶贮槽混合熵与塔顶贮槽内液体混合熵产，kJ·K−1·kmol−1

xD、xDe——分别为精馏过程与终了时，塔顶贮槽液体中轻组分的摩尔分数

ΔxD——xD由xF变为xDe的精馏过程的离散距离

xD,i、——分别为第i段后塔顶贮槽液体中轻组分的摩尔分数与第i段塔顶贮槽液体中轻组分的平均摩尔分数

xF——原料中轻组分的摩尔分数

xW、、xWm——分别为底出料中轻组分的瞬时摩尔分数、第i段塔底出料中轻组分的平均摩尔分数与塔底产品中轻组分的平均摩尔分数

yD——与xD平衡汽相中轻组分的摩尔分数

α——相对挥发度

ηh——塔底产品中重组分的收率

ε——收敛精度

φ、φa,i、φt——分别为瞬时、第i段平均与总平均能耗效率

ωs——固定单步长因子梯度法的步长因子

ωin、ωout——分别为固定双步长因子梯度法的内循环与外循环的步长因子

ωin,c——可收敛至约束条件的内循环最大步长因子

上角标

0,0——数值计算时，各物理量的初值

s,ss——计算程序的第ss次外循环中s次内循环时各物理量的值

下角标

i、j——数值计算时，第i段与第j段各物理量的值

opt ——优化操作时，各物理量的值

min ——N+1→∞时，各物理量的值

xW=C——恒残液组成操作时，各物理量的值

[1] Editorial Committee of Handbook Chemical Engineering (《化学工程手册》编辑委员会). Handbook Chemical Engineering (化学工程手册) [M]. Beijing: Chemical Industry Press, 1989.

[2] Robinson C S, Gilliland E R. Elements of Fractional Distillation [M]. 4th ed. New York: McGraw-Hill, 1950.

[3] Hasebe S, Abdul-Aziz B B, Hashimoto I, Watanabe T. Optimal design and operation of complex batch distillation column//Proceedings of the IFAC Workshop on Interaction between Process Design and Process Control [C]. London, 1992: 177-182.

[4] Mujtaba I M, Macchietto S. Optimal operation of reactive batch distillation//AIChE Annual Meeting [C]. Miami Beach, USA, 1992.

[5] Mujtaba I M, Macchietto S. Optimal operation of multicomponent batch distillation—a comparative study using conventional and unconventional columns//Rreprints IFAC symposium ADCHEM’95 [C]. Kyoto, Japan, 1994: 415-420.

[6] Chiotti O J, Iribarren O A. Simplified models for binary batch distillation [J].Computers & Chemical Engineering, 1991, 15 (1): 1-5.

[7] Chiotti O J, Salomone H E, Iribarren O A. Selection of multicomponent batch distillation sequences [J].Chemical Engineering Communications, 1993, 119 (1): 1-21.

[8] Sorensen E, Skogestad S. Comparison of regular and inverted batch distillation [J].Chem.Eng.Sci., 1996, 51 (22): 4949-4952.

[9] Xu Songlin, Salomone H E, Iribarren O A. Shortcut procedure for inverted batch distillation column (Ⅰ): Multicomponent ideal system [J].Chinese Journal of Chemical Engineering, 2001, 9 (1): 28-33.

[10] Xu Songlin, Espinosa J, Salomone H E, Iribarren O A. Operation of a batch stripping distillation column [J].Chinese Journal of Chemical Engineering, 2001, 9 (2): 141-144.

[11] Zhang Xuemei (张雪梅), Guo Jintang (郭锦棠), Zhang Weijiang (张卫江). Binary stripping batch distillation [J].Journal of Tianjin University(天津大学学报), 2005, 38 (11): 950-954.

[12] Wang Weiguo (王为国), Wu Yuanxin (吴元欣), Wang Cunwen (王存文), Zhen Zhen (曾真). Algorithm of minimum reflux ratio of batch distillation under constant reflux ration and its energy consumption analysis [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2004, 55 (8): 1285-1290.

[13] Wang Weiguo (王为国), Wang Cunwen (王存文), Wu Yuanxin (吴元欣) , Zhen Zhen (曾真). Minimum total vapor capacity of binary regular batch distillation [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2006, 57 (11): 2647-2651.

[14] Wang Weiguo (王为国), Zeng Zhen (曾真), Bi Yafan (毕亚凡). Minimum total vapor capacity of batch distillation of binary mixture under total reflux and top accumulation [J]. Journal of Chemical Industry and Engineering(China) (化工学报), 2001, 52 (5): 460-463.

[15] Wang Weiguo (王为国), Zeng Zhen (曾真), Bi Yafan (毕亚凡), Sun Wei (孙炜). Mixing of flowing liquid in top vessel with batch distillation under total reflux [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2002, 53 (8): 857-861.

[16] Wang Weiguo (王为国), Wang Cunwen (王存文), Wu Yuanxin (吴元欣), Zeng Zhen (曾真). Energy consumption of batch distillation of binary mixture under “total reflux” [J].Journal of Chemical Industry and Engineering(China) (化工学报), 2004, 55 (9): 1474-1480.

[17] Wang Weiguo, Wang Cunwen, Zhou Fanglei, Qin Yuanhang, Wu Yuanxin, Zeng Zhen. Energy consumption in binary batch distillation of total reflux and top accumulation [J].Advanced Material Research, 2012, 396: 699-705.

[18] Wang Weiguo (王为国), Zeng Zhen (曾真), Wang Cunwen (王存文), Wu Yuanxin (吴元欣). Minimum theoretical trays for binary batch distillation under total reflux and top accumulation [J]. Petrochemcal Technology(China) (石油化工), 2011, 40 (11): 1205-1210.

[19] Wang Weiguo (王为国), Zeng Zhen (曾真), Qin Yuanhang (覃远航), Wang Cunwen (王存文), Wu Yuanxin (吴元欣). Energy consumption analysis and minimum reboil ratio of stripping batch distillation under constant reboil ratio [J].CIESC Journal(化工学报), 2012, 63 (7): 2106-2112.

[20] Wang Weiguo (王为国), Duan Xiaoling (段晓玲), Zeng Zhen (曾真), Wang Cunwen (王存文), Wu Yuanxin (吴元欣). Shortcut method of stripping binary batch distillation of under constant residual fraction composition [J].Journal of Wuhan Institute of Technology(武汉工程大学学报), 2014, 36 (1): 9-13.

[21] Li Qingyang (李庆杨), Wang Chaoneng (王超能), Yi Dayi (易大义). Numeric Analysis (数值分析) [M]. Wuhan: Huazhong University of Technology Press, 1982.

[22] Xue Yi (薛毅). Optimization Theory and Methods(最优化原理与方法) [M]. Beijing: Beijing University of Technology Press, 2004.

Optimization operation of binary stripping batch distillation and its minimum total evaporation

WANG Weiguo1, LUO Jingsong1, ZENG Zhen2, WANG Cunwen3, WU Yuanxin3, QIN Yuanhang3
(1School of Chemical Engineering and Pharmacy,Wuhan Institute of Technology,Wuhan430074,Hubei,China;2School of Mechanical and Electrical Engineering,Wuhan Institute of Technology,Wuhan430074,Hubei,China;3Key Laboratory for Green Chemical Process of Ministry of Education,Wuhan Institute of Technology,Wuhan430074,Hubei,China)

Under ideal operation conditions, the calculation for total evaporation and the minimum total evaporation of binary stripping batch distillation under optimal operations is a constrained function optimization problem. In this work, the constrained function optimization problem is transformed to an unconstrained function optimization problem based on the penalty function method and the fixed double step length factor gradient method is used to solve the unconstrained optimization problem. The calculations show that the fixed double step length factor gradient method has good convergence, and the effect of numerical truncation error accumulation on the calculation results is reduced when the number of segments is large. The energy consumption of binary stripping batch distillation under optimal operation is lower than that under constant residual fraction composition operation. It may be attributed to the following reasons: when the theoretical plate number is relatively small (close to the minimum theoretical plate number required for binary stripping batch distillation under constant residual fraction composition operation), the energy efficiency is improved because of controllable reboil ratio under the optimal operation; when the theoretical plate number is relatively large, the entropy generation in liquidmixing in the top tank is reduced because the material is removed out of the distillation system as soon as possible in the premise of relatively high energy efficiency under the optimal operation because of the controllable reboil ratio. Under ideal operating conditions and infinite number of theoretical plates, the change strategy of the reboil ratio and the calculation formula of the minimum total evaporation of binary stripping batch distillation under optimal operation are obtained by summarizing and extrapolating the above calculation results.

stripping batch distillation; optimal operation; total evaporation; simulation; energy consumption

ZENG Zhen, zengzhen415@126.com

10.11949/j.issn.0438-1157.20141687

TQ 015

：A

：0438—1157（2015）10—4047—14

2014-11-12收到初稿，2015-04-30收到修改稿。

联系人：曾真，副教授。

：王为国（1963—），硕士，副教授。

Received date: 2014-11-12.