摆线齿轮齿廓的法向极坐标测量及误差分析＊

梁 巍，王建华

（西安工业大学 机电工程学院，西安710021）

摆线齿轮广泛应用于摆线针轮行星减速器和各种形式的摆线泵中，作为这些机器的关键零件，摆线齿轮的几何精度直接影响着这些机器的性能．摆线齿轮的几何精度由加工精度和测量精度共同决定．在摆线齿轮的测量过程中，测球的球度误差和测杆的受力变形均会引入测量误差，从而影响测量精度．

为了测量摆线齿轮，传统的测量方法通常采用特殊点检测法［1-5］．该测量方法只能反映摆线齿轮的部分参数误差，无法评定摆线齿轮的齿廓精度．为实现摆线齿轮齿廓偏差的自动测量，文献［6］提出在三坐标测量机上测量摆线齿轮齿廓偏差，通过三坐标测量机上测得齿廓的各点坐标值后，以最小齿廓法向偏差平方和为目标函数，对设计齿廓坐标系与坐标机坐标系的夹角进行优化，以计算各项齿轮误差．文献［7］提出在极坐标测量仪上测量摆线齿轮齿廓偏差，与三坐标测量机相比极坐标测量仪效率高且精度稳定．极坐标测量仪由旋转轴和直线轴组成测量坐标系，将摆线齿轮安装在极坐标测量仪的回转工作台上其轴心与工作台轴心重合，测球沿径向放置在直线轴位置．测量时工作台带动摆线齿轮转动，同时齿轮推动测球伸缩，测量系统实时采样工作台转角值和测球示值，根据采样到的一系列数据与摆线齿轮的理论齿廓数据比较可测得齿廓偏差．文献［8-9］在此基础上提出在直线轴加入一个驱动电机，使得当工作台旋转时，根据齿廓曲线主动控制测球运动以减小测球的受力，从而相应地减少了测杆的受力变形，同时也减小了测球的磨损．由于测球测力方向和受力方向不一致，此方法中测杆的受力变形仍然影响齿廓法向误差．

为减小摆线齿轮测量过程中测球的球度误差和测杆的受力变形对齿廓法向误差的影响，文中通过分析球度误差和测杆受力变形对齿廓法向误差的影响，对传统极坐标测量法的齿廓偏差数学模型进行改进，得到齿廓曲线在法向极坐标系中的参数方程和齿廓偏差的数学模型，比较法向极坐标法与极坐标法的齿廓法向误差，以期为摆线齿轮齿廓测量方法优选提供参考．

1 齿廓的极坐标测量

1．1 极坐标测量法

极坐标法测量坐标系由一个以O为轴心的旋转轴和一个直线轴R组成，齿轮轴心与O点固连，如图1所示，将任意齿齿根点作为起始测量点，起测点A的极角φ0＝0°，极径ρ0为齿根圆半径，其极坐标为（0，ρ0），采用测力方向为R向的测球．图2为极坐标法测量原理图，图2中测球在测点M（φ，ρ）法矢方向上的受力为Fe，在R向上的测力为F，测球的测力F和Fe之间的夹角α称为测量压力角．根据摆线的形成原理，滚圆相对于基圆所转过的角度称为啮合相位角φHP，啮合相位角φHP由0°增加到360°形成一个齿［10］，形成n个齿时，啮合相位角φHP由0°增加到n×360°．

图1 极坐标法测量起始点Fig．1 Starting point of polar coordinate method

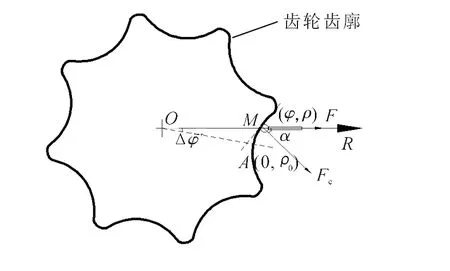
图2 极坐标法测量原理Fig．2 Measuring principle of polar coordinate method

测球沿理论齿廓曲线运动一周，其球心点的轨迹曲线为齿廓曲线的等距曲线，称此轨迹曲线为测球中心轨迹曲线，其极坐标方程［8］为

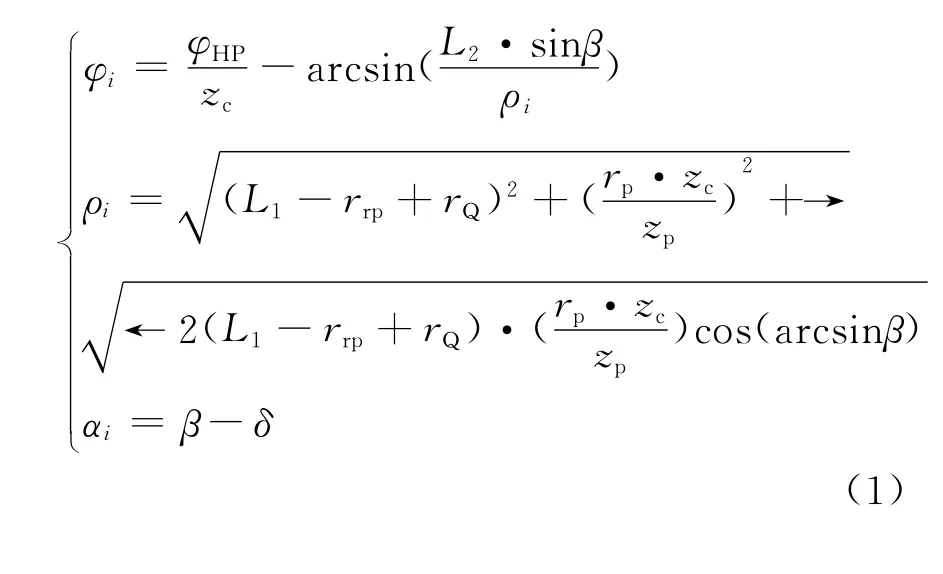
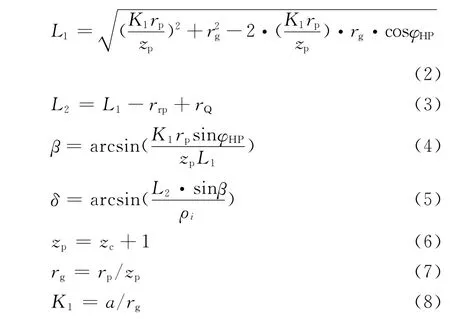
式中：rp为创成圆半径；rg为滚圆半径；zc为摆线齿轮齿数；zp为外转子齿数；a为偏心距；L1，L2，β，δ均为中间变量；rQ为测球半径；rrp为针齿半径；K1为短幅系数；测球中心轨迹曲线的离散点极坐标记为（φi，ρi）；αi为第i个离散点处的测量压力角．

控制测球沿测球中心轨迹曲线运动一周即可完成对摆线齿轮齿廓的采样．采用等啮合相位角φHP得到的测球中心轨迹曲线离散点分布比较均匀，故将等分的φHPi（i＝1，2，3，…，k）代入式（1）即可得到一系列离散点的极坐标（φi，ρi）（i＝1，2，3，…，k）．在测量过程中，当摆线齿轮转动到极角φi时，测球沿R轴运动到极径ρi，从而可以控制测球沿理论齿廓曲线运动一周．例如测量图2中点M，其极坐标为（φ，ρ），齿轮由图1所示的起测点（0，ρ0）顺时针旋转Δφ＝φ-0°角，同时测球沿R向由齿根位置位移Δρ＝ρ-ρ0，此时测球由初始位置运动到点M．

在测球沿理论齿廓曲线运动一周的过程中，测球连续采样得到一系列采样点（φj，ρj′）（j＝ 1，2，3，…，n）和各采样点处的测量压力角αj，将极径方向的偏差转化为法向偏差ej，有

其中ρj为第j个采样点的理想极径．

由于理想采样点和实际采样点均分布在测球中心轨迹曲线上，故径向偏差即可以反映齿廓偏差，不需要换算到齿廓曲线上进行误差的计算．

1．2 齿廓极坐标测量误差影响因素分析

采用极坐标法测量摆线齿轮1号齿的齿廓，分析齿廓极坐标测量中测球的受力，如图3所示．

图3 齿廓的极坐标测量中测球的受力分析Fig．3 Stress analysis of measuring ball in polar coordinate measurement of tooth profile

若齿轮顺时针方向旋转，在测量过程中齿廓与测球的接触点是不断变化的．图3（a）中1号齿的右齿面与测球上的点A接触，此时测球的受力为FA，方向沿接触点处的法矢方向，FA在R轴方向和R轴的垂直方向的分力分别为F1和F2，分力F2会使得测杆变形；这里测球的受力方向（法矢方向）和R轴方向之间的夹角即是上述的测量压力角α，α越大，F2越大，测杆的变形也越大．同理，图3（b）中1号齿的左齿面与测球上的点B接触，此时测球的受力为FB，方向沿接触点处的法矢方向，FB在R轴方向和R轴的垂直方向的分力分别为F1′和F2′，分力F2′也会使测杆变形．测杆的变形会导致测球的实测点偏离理论点，实测点与理论点在径向（R向）的偏差便是测量误差．随着测球与齿廓接触点的变化测球受力的大小和方向也不断的变化，特别是当测量压力角α较大时，测球的实测点偏离理论点显著．

如上所述，采用测力方向为R方向的测球，测球有一个基本行程，在基本行程中存在一个零位和两个极位，如图4所示，若一个测球的测量行程为-0．365 ～ ＋0．365mm，测球的悬空状态在-0．365mm极位处，测球与理想齿廓接触，应被压到零位处，当齿廓偏差为正偏差时，测球的压入量会变大，此时示值变大；当齿廓偏差为负偏差时，测球会沿R负向运动，此时示值负向增大．由于极坐标法在测量过程中齿廓与测球的接触点是不断变化的，故当测球存在球度误差时会影响测量精度．假设齿廓为理想齿形（不存在误差），测量时当接触点处测球的球度误差为负值（测球磨损属于此情况），此时测球会负向偏离零位，偏离值即为测量误差；当接触点处测球的球度误差为正值时，测球会正向偏离零位，偏离值即为测量误差．

图4 测球行程Fig．4 Measuring-ball trip

在测量过程中齿轮始终顺时针方向旋转，在测量右齿面时，如图3（a）所示，测球沿R正向退出，齿廓的旋转是压着测球运动，而在左齿面时，如图3（b）所示，测球沿R负向进给，测球是追着齿轮旋转运动．也即在测量过程中，左右齿面的运动是不对称的，这造成了以齿顶为中心的对称点处测球的受力大小不等，且方向不对称，如图3中FA和FB所示，其FA应大于FB．测力大小不相等会产生示值误差，影响齿廓误差．图3中FA和FB分别旋转测量压力角α，此时测球与齿廓接触点的法矢方向旋转到与R轴平行（α＝0）位置，此时F2和F2′为零，测球受力全部用于推动测球在行程内的运动，测杆的受力变形也随即被消除．为使测球与齿廓接触点的法矢方向与R轴平行（测量压力角α始终为零），本文提出摆线齿轮齿廓的法向极坐标测量法．

2 齿廓的法向极坐标测量

为使测量压力角α始终为零，在极坐标测量系中加入了一个垂直于R轴的直线轴T，如图5所示，φ为极角．采用法向极坐标法测量图2中点M，当齿轮由图2所示状态逆时针旋转α角后，测力Fe平行于水平方向（平行于R轴），此时满足测球的测力方向与受力方向（测球与齿廓接触点处法矢方向）一致且平行于R轴．若由起测点开始测量，齿轮应首先顺时针转动Δφ后，又逆时针转动α，故测量点M时旋转轴由起测点最终转过的角度θ＝α-Δφ＝α-φ．在齿轮转动过程中，为使测球运动到点M，测球在旋转轴运动的过程中同时需要沿R方向和T方向共同运动，沿两个方向的运动距离分别为r和t，由图5可得r＝ρcosα，t＝ρsinα．对于齿廓曲线上每一个点的极坐标值（φi，ρi）都对应一个法向极坐标值（θi，ri，ti），且满足关系

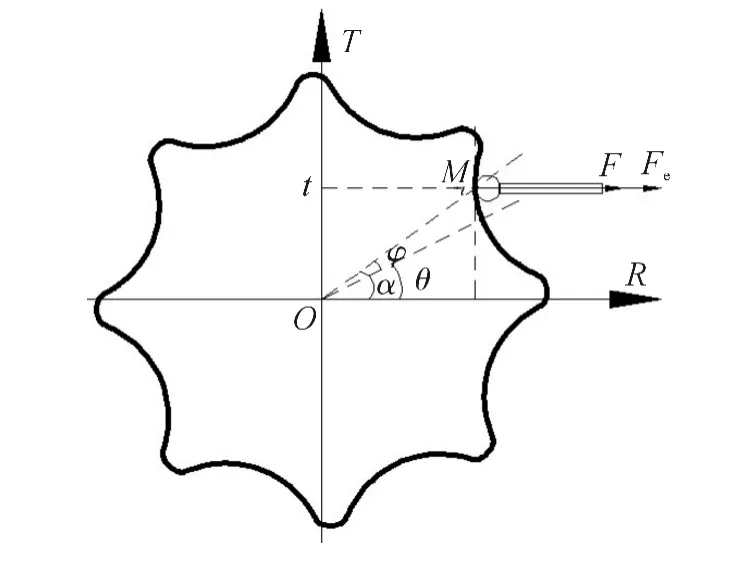
图5 法向极坐标法测量原理Fig．5 Measuring principle of normal polar coordinate method

由式（10）可以得到整周齿廓曲线上的运动点的法向极坐标值（θi，ri，ti）（i＝ 1，2，3，…，k），控制测球连续由一个点运动到下一个点，这样测球便可沿一个整周齿廓曲线运动，在运动过程中测球进行连续采样得一系列采样点（θj，rj′，tj′）（j＝ 1，2，3，…，n）．若各采样点的理论值为（θj，Rj，Tj），由于在测量过程中法矢方向始终平行于R轴，故法向偏差值可根据R向的实际测量值rj′和理想值Rj之差来确定．齿廓偏差为

在齿廓法向极坐标测量过程中齿廓与测球的接触点始终不变，即图5中测球上与齿廓上点M接触的点（即测球顶点）．由于接触点始终不变，故即使接触点（测球顶点）处测球存在球度误差，它对每一个采样点的影响是相同的，可通过测量测球顶点处的球度误差将球度误差的影响消除．

3 测量实例及分析

实验采用D40型齿轮测量中心（西安共达精密有限公司）为测量平台，该仪器测量精度高，能够满足实验要求．试验中测球采用柱塞式测球，其测球的测量范围为 -0．368～＋0．368mm，安装完成后其测力方向沿测量中心的R轴方向．

本实验所采用齿轮为与圆弧啮合的摆线齿轮，其基本参数见表1．采用法向极坐标法和极坐标法在同一次装夹定位下对该摆线齿轮进行测量，每个齿取100个运动点，200个采样点，以齿根点作为测量的起始点，齿轮顺时针转动进行测量．

采用法向极坐标法原理测量摆线齿轮时，齿廓偏差检测结果如图6（a）所示；极坐标法测量时，齿廓偏差检测结果如图6（b）所示．图6中实线为理论齿廓曲线，虚线为实际齿廓曲线，1～8为齿编号；X，Y为测量坐标刻度．

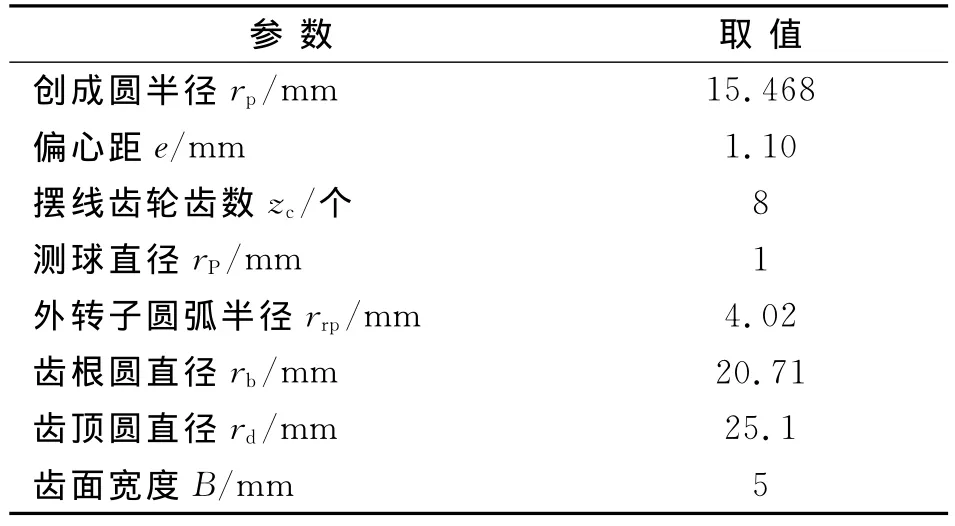
表1 摆线齿轮基本参数Tab．1 The basic parameters of cycloidal gear

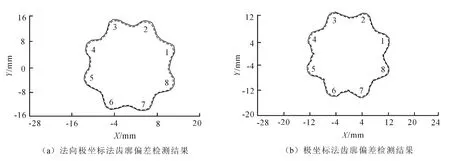
图6 齿廓偏差检测结果Fig．6 Detection results of tooth profile deviation

摆线齿轮每个齿有一个齿廓总偏差，反映了该齿上的齿廓偏差的幅值（该齿上齿廓偏差的最大值与最小值的代数差）．

采用两种不同测量方法得到的齿廓总偏差如图7所示．

图7 不同齿廓测量方法得到的齿廓总偏差Fig．7 Comparison of tooth profile error between polar coordinate method and normal polar coordinate method

从图7可发现，法向极坐标法检测得到的各个齿的齿廓总偏差均小于极坐标法，表明齿轮齿廓检测时，法向极坐标测量法较极坐标测量法的齿廓总偏差小．

这说明采用法向极坐标法测量齿廓偏差时，测杆受力变形所引入的测量误差和测球球度误差对测量结果的干扰较极坐标法小．故摆线齿轮齿廓的法向极坐标测量比极坐标测量精度高．

4 结 论

本文分析测球球度误差和测杆受力变形对摆线齿轮齿廓极坐标测量的影响，提出了齿廓法向极坐标测量法，通过齿轮测量中心获得了摆线齿轮全齿廓上各测量点的齿廓偏差，得出的结论为

1）采用法向极坐标法测量齿廓时，齿廓测量点的法矢方向和测球的测力方向保持一致，测杆变形所引入的测量误差较极坐标法小，测杆受力变形对齿廓测量精度的影响较极坐标法减小．

2）在法向极坐标法测量过程中，测球与齿廓的接触点始终不变，球度误差对每一采样点的齿廓法向误差的影响程度相同；在实验数据处理过程中，每一采样点的齿廓偏差减去测球顶点的球度误差，测球球度误差所引起的齿廓法向误差较极坐标法小．

3）法向极坐标法测量摆线齿轮左右齿面的齿廓偏差时，每一采样点处测球测力大小相等，测杆在接触点法矢方向上的变形对齿廓法向误差的影响得以消除．

［1］ 周玉华，吴娟．摆线齿轮齿形的测量方法与工艺分析［J］．鞍山钢铁学院学报，2001，24（1）：15．ZHOU Yu-hua，WU Juan．Process Analysis and Measurement Method of Cycloid Gear Tooth Profile［J］．Journal of Anshan Institute of Iron ＆ Steel Technology，2001，24（1）：15．（in Chinese）

［2］ 张建军，梁锡昌．行星摆线齿轮的公法线尺寸的确定方法［J］．重庆大学学报，1987，4（2）：10．ZHANG Jian-jun，LIANG Xi-chang．The Method to Determine the Common Normal Line Size of Planetary Cycloidal Gear［J］．Journal of Chongqing University，1987，4（2）：10．（in Chinese）

［3］ 方素平，林其骏．任意齿数的摆线齿轮公法线长度的计算与测量［J］．机械制造，1987，6：6．FANG Su-ping，LIN Qi-jun．Calculation and Measurement of Common Normal Length of Cycloidal Gear with any Number of Teeth［J］．Machinery Manufacturing，1987，6：6．（in Chinese）

［4］ 关天民，李力行．摆线轮双棒量法尺寸的确定方法［J］．大连铁道学院学报，1989，10（2）：45．GUAN Tian-min，LI Li-xing．Method for Determining the Size of Cycloid Wheel by Double Rod Measurement Method［J］．Journal of Dalian Railway Institute，1989，10（2）：45．（in Chinese）

［5］ 王庭树，张先承．摆线齿轮齿形误差的间接检测法［J］．机床，1984（4）：9．WANG Ting-shu，ZHANG Xian-cheng．Indirect Detection Method of Cycloidal Gear Tooth Errors［J］．Machine Tool，1984（4）：9．（in Chinese）

［6］ 翟海云，毕锋杰．三坐标测量机测量摆线轮误差的数据处理方法［J］．计量技术，1998（9）：5．ZHAI Hai-yun，BI Feng-jie．Data Processing Method of Cycloidal Gear Error Measured by Three Coordinate Instrument［J］．Measurement Technology，1998（9）：5．（in Chinese）

［7］ 宋建峰．微型机控制摆线齿轮齿形误差自动测量［D］．天津：天津大学，1985．SONG Jian-feng．Microcomputer Control Measurement of Cycloidal Gear Profile Error［D］．Tianjin：Tianjin University，1985．（in Chinese）

［8］ 郭敬滨，王娴，周广才，等．摆线齿轮极坐标径向跟踪测量技术的研究［J］．工具技术，2010，44（1）：91．GUO Jing-bin，WANG Xian，ZHOU Guang-cai，et al．Study on Radial Tracking Measuring Technology of Cycloidal Gear in Polar Coordinates［J］．Tool Engineering，2010，44（1）：91．（in Chinese）

［9］ 郭敬滨，王娴，刘海军，等．摆线齿轮极坐标跟踪测量关键技术的研究［J］．计量学报，2010，31（6）：494．GUO Jing-bin，WANG Xian，LIU Hai-jun，et al．Study on the Key Technology of Tracking Measurement of Cycloidal Gear［J］．Acta Metrologica Sinica，2010，31（6）：494．（in Chinese）

［10］ 齿轮手册编委会．齿轮手册［M］．2版．北京：机械工业出版社，2001．Gear Guide Editorial Board．Gear Guide［M］．2nd ed．Beijing：Machinery Industry Press，2001．（in Chinese）