平行钢绞线索力测试的参数识别方法

吴 霄，肖汝诚

（同济大学土木工程学院，上海200092）

平行钢绞线索力测试的参数识别方法

吴 霄，肖汝诚

（同济大学土木工程学院，上海200092）

针对平行钢绞线测索力存在的问题，提出基于拉索非线性振动分析的参数识别新方法.建立考虑拉索垂度及抗弯刚度的拉索振动非线性微分方程，并引入多尺度法求解拉索非线性振动问题，得到基频计算实用公式.采用公式对比与有限元分析的手段，验证该公式的准确性.以该公式为基础，对平行钢绞线斜拉索索力、索长、线密度以及抗弯刚度等的参数识别问题进行了研究，提出采用参数识别方法计算其索力.结果表明：所获得的基频计算公式简单实用，能同时考虑拉索抗弯刚度与垂度的共同影响，满足精度要求；平行钢绞线索力测试的参数识别方法能够准确、方便地确定拉索设计参数，易于模块化设计，显著提高了拉索测试精度.

平行钢绞线；索力测试；非线性振动；多尺度法；参数识别

平行钢绞线索因其加工制作便捷、施工方便、可分批次张拉、耐久性能好、便于更换、强度高、经济性好等特点，在斜拉桥建造中越来越多地被使用，如南京江心洲大桥.索力测量是斜拉桥施工监控与后期运营监测的一项重要内容，频率法是目前索力测试中应用最广的方法［1-2］.频率法应用于平行钢绞线斜拉索的索力测量时，可能存在以下问题：由于忽略拉索的垂度、刚度等影响，基于线性振动理论得到的拉索动力响应可能存在较大偏差；施工阶段与运营阶段拉索形态是不同的，单根钢绞线与整束拉索的索力测量方式不同；运营阶段拉索外套HDPE套管对索力测试可能存在不可忽略的影响.文献［3］证明了频率法能够应用于平行钢绞线斜拉索索力测试，分析了HDPE套管对索力测试的影响，但文中未考虑拉索及套管抗弯刚度的影响.文献［4］初步探讨了拉索非线性振动的多尺度解法，提出了考虑拉索垂度与抗弯刚度的索力测试实用公式.本研究在此研究基础上，通过数值分析，验证公式的准确性、有效性和适用性，进而以该公式为基础，结合南京江山大街过江通道步行桥施工监控项目，探讨基于频率法的平行钢绞线斜拉索索力测试.

1 索的非线性振动微分方程

考虑拉索的抗弯刚度，索在自重及轴向力作用下的静力平衡方程为

式中：EI为索的抗弯刚度；N为索轴向力；ws为索的挠度曲线.

假设N为常数，索单元两端为简支，根据索挠度曲线［5］可得

将上式用傅里叶级数展开为

其中wi为傅里叶系数，可表示为

由式（4）可知：若i为奇数，wi存在；若i为偶数，则wi为0，将式（4）代入式（2）可得

平行钢绞线斜拉索的振动是在其静力平衡位置附近的振动，因此索在振动时的挠度由2部分组成：静力平衡位置的挠度ws（x）和随时间变化的动位移wd（x）［6］，即

其中wd（x）可由下式表示：

其中an（t）为动位移傅里叶系数.总的挠度表示为

这里i与n等效，考虑拉索振动引起的索力增量，索振动的微分方程为［5］

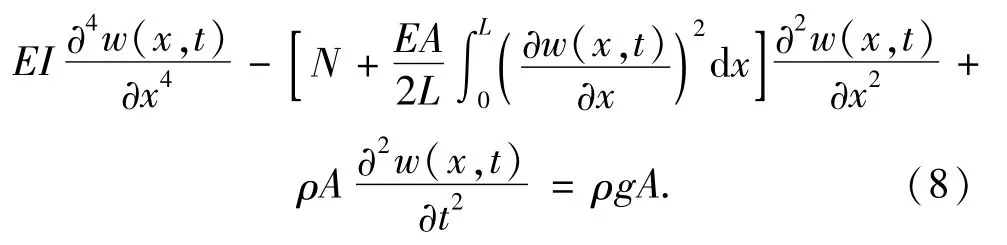
将式（7）代入式（8），可得

式中：

2 非线性振动微分方程的求解

式（9）为单自由度非线性振动的微分方程，方程系数gn1，gn2，gn3可表示为

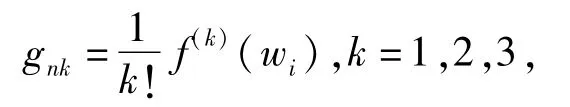
其中f（k）（wi）为

式（9）符合多尺度法解微分方程的典型形式，利用多尺度法，可得该非线性微分方程的解为

其中wn为系统非线性振动的固有角频率，即

假设振动的初位移及初速度为激励的振幅与相位的函数，即

式中为初始激励的振幅；βn0为初始激励的相位.取t=0，联立式（7）与式（9），可得

在施加外部激励时，一般取βn0=0，此时初位移即为振幅，初速度为仅与初始振幅有关.

式（11）计算索力需已知索的初始振幅，实际应用过于复杂.由式（11）可知，索的非线性基频主要由2部分组成，一部分是线性基频，另一部分是非线性基频影响部分，该部分由线性基频乘以非线性效应系数组成.基频的非线性效应系数受gn1及初始振幅的共同影响.根据式（9），量纲一的特征参数ξ2=及长细比L/r又是影响gn1大小的主要因素.文献［4］通过分析初始振幅、ξ2及长细比等参数对拉索非线性基频的影响，认为在ξ2＞2 500时，可忽略初始振幅、ξ2及长细比等参数对拉索非线性基频的影响，直接采用线性基频计算公式计算拉索基频，拉索线性基频计算公式可表示为

考虑到工程中超过95％的斜拉索的特征参数ξ2＞2 500［6］，可认为上述基频公式具有实用性.

3 公式验证

1）公式对比验证.参考常用的索力计算公式，对比本研究线性及非线性基频计算公式，对式（13）的准确性及有效性进行验证.非线性基频计算时取ζ=1，常用的索力计算公式参考文献［1，7］及弦理论计算公式.

图1为各种计算公式下的索力计算公式比较.

图1 各种索力计算公式比较

由图1可知，几种索力计算公式中，在索力较大时，均接近于弦理论计算公式，弦理论计算结果略小于H.Zui等［1］提出的公式，这是因为Zui公式中考虑了抗弯刚度的影响；索力较小时，Zui公式与弦理论由于未考虑拉索线密度影响，误差较大；A.B.Mehrabi和H.Tabatabai［7］提出的计算公式采用了有限差分法，同时考虑了拉索抗弯刚度与垂度的影响，与本研究采用的线性基频计算值最为接近.

2）数值分析验证.通过数值分析对式（13）的准确性及有效性进行验证.拉索参数EA=957 543 kN，EI=731 kN·m2，L=62 m，单位长度重量q= 0.58 kN·m-1，由于长细比是影响拉索频率的主要参数，取长细比分别为100，500，1 000，2 000和10 000，索力设计值取2 000 kN，利用Ansys建立了拉索振动的有限元模型，考虑抗弯刚度的索用Beam44单元来模拟，索边界条件采用简支，分析结果如表1所示.

表1 拉索基频计算结果对比

由表1可知：式（13）计算结果与有限元仿真分析结果存在一定的误差，主要是由于式（13）在求解拉索静力平衡线形时作了相应近似，略去了高阶小量，各项误差均在3％以内，表明式（13）满足工程精度要求，可作为振动法测索力以及拉索动力特性研究的依据.

4 索力测试

平行钢绞线因其构造特性，施工阶段与运营阶段拉索形态是不同的，单根钢绞线与整束钢索索力测试方法也不同.对于施工阶段的单根钢绞线，由于其直径较小，可忽略抗弯刚度及垂度的影响，按照弦理论计算公式计算索力，或者直接根据油压表读数测量单根钢绞线张拉力；运营阶段多根钢绞线汇成整束拉索，外套HDPE套管，其截面较大，忽略抗弯刚度以及垂度会引起较大误差，而拉索的抗弯刚度、线密度及拉索计算长度难以准确确定，无法直接采用式（13）计算.为此本研究以式（13）为基础，采用参数识别方式计算拉索索力.

由式（13）可知，振动频率受N，EI，ρA以及L影响，取这4个参数为待识别量，将参数识别问题转化为有约束的最优化问题［8］.目标函数与约束条件如下所示：

通过惩罚函数将式（14）转化为无约束的最优化问题，进而采用多种算法进行求解，本研究采用遗传算法［9-10］.对于本例，定义初始种群数、最大迭代次数及交叉变异系数后，首先利用遗传算法生成初始种群，根据式（13）计算初始种群下的基频，然后按照遗传算法计算程序进行选择、交叉、变异操作，对得到的新种群重新计算其基频，评价其是否满足终止条件，若不满足则继续按照上述程序进行计算，最终得到拉索真实设计参数，其参数识别过程如图2所示.

图2 参数识别过程

5 索力测试的工程应用

南京江山大街过江通道步行桥主桥采用主跨240m钢箱梁斜拉桥，斜拉索采用1 860 MPa平行钢绞线斜拉索，主跨侧拉索采用型号15-27，15-31和15-34斜拉索；边跨侧背索采用型号15-55斜拉索.图3为其主桥立面图.图4为基频值比较.

图3 南京江山大街过江通道步行桥主桥立面布置图（单位：cm）

图4 基频实测值与计算值比较

利用前文编制的遗传算法计算程序在matlab中进行参数识别.优化目标为基频计算值与测量值平方差最小.在给定的参数变化范围内，取初始种群数量为100，最大迭代次数为500，交叉概率为0.9.首先利用遗传算法产生初始种群，计算初始种群下的目标值，然后按照前文所述法则进行选择、交叉和变异操作，对得到的新种群重新计算其目标值，评价其是否满足终止条件，若不满足则继续按照上述程序进行计算，最终得到一组最优参数值.按照上述程序逐一对Z1-Z8拉索进行计算，最终得到全部拉索的真实设计参数（见表2）.

表2 拉索参数识别结果对比

识别后拉索索力误差为1.54％～0.21％，满足实际工程需要，可根据基频计算索力；基频计算值与实测值误差范围在0.56％以内，说明识别的参数接近于拉索真实参数.

6 结 论

1）本研究提出的索力计算公式能够同时考虑拉索抗弯刚度以及垂度的影响，计算简便，物理意义明确，精度高，可作为拉索参数识别研究的依据.

2）本研究中的平行钢绞线索力测试的参数识别方法能准确、方便地确定拉索设计参数，能和索力计算公式组成完整的方法体系，便于模块化设计.

（

）

［1］Zui H，Shinke T，Namita Y.Practical formulas for estimation of cable tension by vibrationmethod［J］.Journal of Structural Engineering，1996，122（6）：651-656.

［2］Dong-Ho Choi，Wan-Soon Park.Tension force estimation of extradosed bridge cables oscillating nonlinearly under gravity effects［J］.International Journal of Steel Structures，2011，11（3）：383-394.

［3］赵云鹏.基于频率法的平行钢绞线斜拉索索力测试研究［D］.郑州：郑州大学土木工程学院，2013.

［4］吴 霄，肖汝诚.考虑垂度及抗弯刚度影响的斜拉桥索力测试［J］.华中科技大学学报：自然科学版，2014，42（3）：92-95 Wu Xiao，Xiao Rucheng.Tension force estimation for cable-stayed bridge under both sag and bending stiffness effect［J］.JHuazhong Univ of Sci&Tech：Natural Science Edition，2014，42（3）：92-95.（in Chinese）

［5］Shih CF，Chen JC，Garba J.Vibration of a large space beam under gravity effect［J］.AIAA Journal，1986，24（7）：1213-1216.

［6］TabatabaiH，Mehrabi A B，Wen-huei PY.Bridge stay cable condition assessment using vibration measurement techniques［C］∥Non-Destructive Evaluation Techniques for Aging Infrastructure&Manufacturing.Atlantic City：International Society for Optics and Photonics，1998：194-204.

［7］Mehrabi A B，Tabatabai H.Unified finite difference formulation for free vibration of cables［J］.Journal of Structural Engineering，ASCE，1998，124（11）：1313-1322.

［8］叶 春，程 进.基于遗传算法的预应力混凝土连续梁桥自动配束方法［J］.结构工程师，2009，25（5）：47-50. Ye Chun，Cheng Jin.Automatic distribution of steel bunches of pre-stressed concrete continuous beam bridge based on the genetic algorithms［J］.Structural Engineering，2009，25（5）：47-50.（in Chinese）

［9］张清华，冉志红，卜一之.拉索非线性振动问题求解及参数识别方法研究［J］.土木工程学报，2009，42（6）：86-91. Zhang Qinghua，Ran Zhihong，Bu Yizhi.Theory and parameter estimation for nonlinear vibration of cables［J］.China Civil Engineering Journal，2009，42（6）：86-91.（in Chinese）

［10］唐爱坤，潘剑锋，陈春伟.基于改进遗传算法的汽车散热器优化设计［J］.江苏大学学报：自然科学版，2008，29（5）：424-427. Tang Aikun，Pan Jianfeng，Chen Chunwei.Optimal design of automotive radiator based onmodified genetic algorithm［J］.Journal of Jiangsu University：Natural Science Edition，2008，29（5）：424-427.（in Chinese）

（责任编辑 赵 鸥）

Tension force estimation for parallel strand cable based on parameter identification method

Wu Xiao，Xiao Rucheng
（College of Civil Engineering，Tongji University，Shanghai200092，China）

To solve the difficulty of tension force estimation for parallel strand cable，parameter identification method was proposed based on the nonlinear vibration of cable.Considering the effects of sag and bending stiffness，the nonlinear vibration differential equation of cable was established.The multiple-scale method was introduced to solve the difficulty and establish a practical formula.The accuracy of the proposed practical formula was verified by comparing the resultswith thosementioned in the literature and the FEM calculation.Based on the formula，parameter identification method for tension force estimation of parallel strand cable including tension，length，density and rigidity was proposed.The results show that the proposed formula is simple and practical，and the key parameters can be identified accurately by parameter identification method with notably improved estimation accuracy.

parallel strand cable；tension force estimation；nonlinear vibration；multiple-scalemethod；parameter identification

U448

A

1671-7775（2015）05-0583-05

吴 霄，肖汝诚.平行钢绞线索力测试的参数识别方法［J］.江苏大学学报：自然科学版，2015，36（5）：583-587.

10.3969/j.issn.1671-7775.2015.05.016

2014-11-17

国家“973”计划项目（2013CB036300）；江西省交通厅重大科研项目（2012C0002）

吴 霄（1986—），男，山东潍坊人，博士研究生（sdwx.328@163.com），主要从事大跨度桥梁施工控制与健康监测系统研究.

肖汝诚（1962—），男，江苏苏州人，教授，博士生导师（通信作者，xiaorc@mail.tongji.edu.cn），主要从事大跨度桥梁结构研究.