时间序列模型在金融学专业教学中的实践与运用研究

谢合亮+袁玥+宋博雅+李家琪

【摘要】时间序列模型是计量经济模型分析中所用的三大类重要模型之一，时间序列数据也是最为常见的一类数据。因此，时间序列模型在金融行业的运用也十分重要，本文将介绍计量经济模型中较为普遍的时间序列模型，对其在教学中的运用进行分析，举出教学案例进行说明并得出结论。

【关键词】时间序列模型 金融专业教学 实践与运用

一、引言

时间序列模型是实证金融模型中的重要组成部分，是时间序列分析在金融各个领域的应用，如股票市场、债券市场、金融衍生工具市场和外汇市场。适用于低频和高频数据;分为时域分析、谱域分析和回归分析集中分析方法;主要研究内容为价格或收益序列的建模，以及相应的波动性或风险的建模。在金融学的教学过程中，采用格林编写的《计量经济分析》，在该教材中，着重介绍了时间序列模型中的ARCH族类模型。ARCH模型是1982年由恩格尔（Engle， R.）提出，并由博勒斯莱文（Bollerslev，T.1986）发展成为GARCH （Generalized ARCH）——广义自回归条件异方差。这些模型被广泛运用在金融时间序列分析中。

二、模型介绍

（一）ARCH模型

自回归条件异方差（Autoregressive Conditional Heterosce- dasticity Model，ARCH）模型是特别用来建立条件方差模型并对其进行预测的。模型公式为：

■ （1）

（二）GARCH（1，1）模型

在标准化的GARCH（1，1）模型中：

■ （2）

■ （3）

其中：xt是1*（k+1）维外生变量向量，γ是（k+1）*1维系数向量。（2）中给出的均值方程是一个带有扰动项的外生变量函数。由于σ2t是以前面信息为基础的一期向前预测方差，所以它被称作条件方差，式（3）也被称作条件方差方程。

（三）高阶GARCH（p，q）模型

高阶GARCH模型可以通过选择大于1的p或q得到估计，记作GARCH（p，q）。其方差表示为：

■ （4）

这里，p是GARCH项的阶数，q是ARCH项的阶数。

三、在金融学专业教学中实践与运用

笔者在本科教学实践过程中，向学生们讲解了时间序列GARCH模型的相关内容，并演示了在计量经济软件eviews6.0下的操作流程。为了让该模型能够得到具体的实践运用和操作，要求学生们完成相关性的论文，有几篇关于时间序列GARCH模型的论文，利用GARCH模型对金融市场上的各类时间序列数据进行具体的检验和参数估计，得出了相应的结果并进行了合理的预测。

（1）在基于时间序列GARCH模型的股票价格波动分析中，利用eviews6.0对采用的2012年4月至2014年2月的上证指数日收盘价取对数进行GARCH模型的参数估计，得出的估计方程如下：

均值方程：■-0.047

（15639.40）

方差方程：■

（4.21）   （3.06） （1.33）

R2=0.96  D.W.=2.10

对未来股票市场趋势预测如下，结论为其股票在未来一段时间会出现下降的趋势。

图1 预测趋势图

图2 解释变量预测

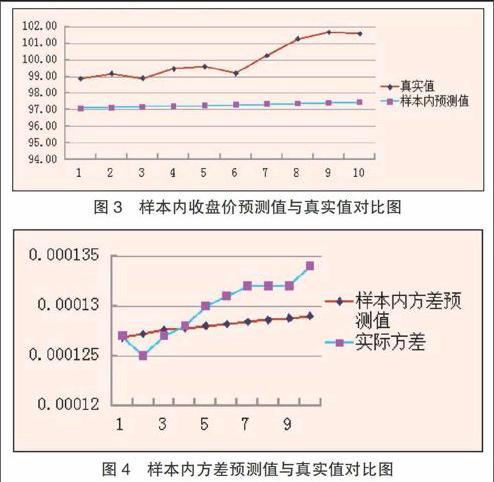
（2）在GARCH模型的预测能力分析—基于国际原油期货价格的研究中，选取UKWTI原油连续合约ET0Y近三个多月（2013.4.12— 2014.4.14）的每日收盘价格，利用时间序列GARCH模型对期货价格进行分析和预测。结果如下图

图3 样本内收盘价预测值与真实值对比图

图4 样本内方差预测值与真实值对比图

该文得出的结论为，GARCH模型对期货价格的预测分析能力较好，对其未来的预测是具有重要作用的。

（3）在实际波动率与GARCH模型的比较分析-基于上交所案例研究中，基于GARCH模型的理论基础及eviews6.0软件进行的对样本数据的分析，建立GARCH（1，1）模型如下：

方差方程：■

条件方差方程：■

（1.50） （0.31）  （12.97）

R2=0.935  D.W.=1.762

对数似然值=742.384 AIC=-6.179 SC=-6.121

从定性上分析，实际波动率选择的样本数据为高频日内收盘价，而GARCH模型选择的样本数据为日内收益的平方，数据采集的频率越高，则理论上与真实值越接近，所以可初步判断实际波动率比GARCH模型具有更高的预测能力。

四、结论

通过在金融学专业教学中的时间与运用研究，学生们能够了解并消化关于教材中时间序列模型的有关内容;能够较为清楚地有条理地对时间序列模型进行分析，得出有意义的结论和预测结果;能够熟练地操作计量经济软件eviews，利用软件对金融数据进行实际有效地处理。

参考文献

[1]龚锐.陈伯常.杨栋锐.GARCH族模型计算中国股市在险价值（Var）风险的比较研究与评述[J].数量经济技术经济研究，2005，（7）：67-83.

[2]郑振龙，黄薏舟.波动率预测：GARCH模型与隐含波动率[J].数量经济技术经济研究.2010，（01）：140-150.

基金项目：防灾科技学院2014年度教研教改项目（JY2014B15）。

作者简介：谢合亮（1982-），男，四川成都人，经济学硕士，防灾科技学院经济管理系讲师;研究方向：计量经济学。