课堂生成性资源的开发与利用
郏丽萍

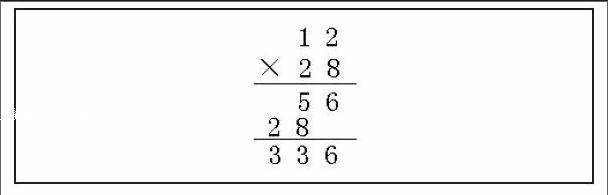
所谓生成性资源不是教师事先准备好的静态备用资源,而是在课堂教学情境中通过积极的师生互动、生生互动、学生与文本对话等活动,在共同思考与共同发展中激发的超出教师教案设计的新问题、新情况,即表现在言语、行为、情绪方式表达中出现的“节外生枝”的学习观点。它具有动态性,是稍纵即逝的。这种教学资源是学生真实体验的反映,是一种非常宝贵的教学资源。准确、及时地捕捉到这些生成性资源并对其加以合理利用,将使课堂教学变得更加精彩。
课堂和谐易于资源生成
学会倾听是资源生成的前提 心灵交融的课堂意义就在于,它能点燃学生和教师智慧的火种。在教学过程中,教师要善于从学生的角度去看待学生的问题和观点。如在教学“简单的时间计算”时,有这样一道题:8:50至9:30播放“金色的童年”,“金色的童年”播放了多少时间?学生独立思考后组织交流,出现了以下计算方法:①8:50过10分钟就到9:00,再过30分就到9:30,一共播放了40分钟。②假如从8:50开始到9:50结束,经过了1小时的时间;实际是9:30结束,比9:50多算了20分钟,1小时-20分钟=40分钟。③也可以用结束时间减开始时间就是播放了多少时间:9时30分-8时50分,9-8=1小时,30分钟减50分钟减不够,1小时+30分钟=90分钟,90分钟-50分钟=40分钟。④以前的减法可以用竖式计算,这里也可以用竖式计算。
减不够,向小时数里借1个小时,就是60分钟,60分钟+30分钟=90分钟,90分钟-50分钟=40分钟,所以9时30分-8时50分=40(分钟)
整个过程中,笔者没有提前透露自己的观点,只是耐心倾听学生们发表想法,尽量满足每只举着的小手,鼓励他们争论,呵护每一位学生的创造力。学生争论不休的时刻,也正是他们参与整个学习活动、经历着数学知识的探索过程的时刻。笔者认为,第四种解题方法,这种独特的见解也正是在主体迷恋执着、充分自由的状态下萌发出来的。
平等对话是资源生成的保障 曾经听过一节《美丽的轴对称图形》讲解课,执教者先要求学生找一找学过的图形当中有哪些是轴对称图形。
生:我认为平行四边形也是轴对称图形。(这一回答教师很意外)
师:能否说说你的想法?
生:因为当平行四边形的四条边都相等时,我把它这样(沿对角线折叠)对折后能完全重合,因此这种特殊的平行四边形是轴对称图形。
(很有说服力,不少学生都不由自主地点头)
师:同学们,他刚才说的话中有一个词用得特别好,知道是哪个词吗?
生1:是“特殊”。其实当平行四边形的四条边都相等时,它就是菱形,是特殊的平行四边形。
师:这是个爱动脑的学生。
生2:一般的三角形不是轴对称图形,但是特殊三角形是。比方说等腰三角形就是轴对称图形。
生3:还有等边三角形。
生4:还有等腰梯形。
生5:所有的圆也是轴对称图形。
正是教师的鼓励和巧妙引导,使学生正确捕捉住轴对称图形的特点,才使数学知识在动态教学中被学生掌握。
用心投入才能运用生成性资源
合理利用生成资源,引发学生认知冲突 教学中有不少易错点,如果在教学时先提醒学生注意,学生反而会忽略,如果直接告诉学生正确的方法,则又很难暴露学生的思维过程,学生也不能真正的学到知识,只有引发学生产生激烈的认知冲突,呈现学生的思维过程,让学生将有争议的认识进行深入思考,才能加深对知识的正确理解,有效避免错误。例如:在教学《两位数乘两位数笔算》时,学生在交流28×12的笔算过程中,能很好地理解每一步的算法和算理,而且通过引导学生得出结论:笔算两位数乘两位数时,其实就是把它分解成两位数乘一位数、整十数来分别计算,然后把两个得数加起来的过程。一切好似顺理成章,学生对算理、算法掌握都很好,于是引导学生进行验算,笔算12×28。结果:部分学生在计算时只是把28×12改成了12×28,每一步的计算结果照抄:
对此,笔者心里很是纳闷,于是在交流时笔者将错就错,直接出示这一错例;真正能理解算理的学生很快就发现了错误;随之组织学生进行讨论、交流,让学生在相互交流中,明确乘数的位置交换了,那么第一步个位算的是8×12=96,而非2×28,第二步十位算的是2×12=24,而非1×28了,因此中间步骤的计算是不同的。在这一过程中,学生注意力集中,真正掌握了算理,达到事半功倍的效果。
深入挖掘生成资源,提升学生思维深度 新教材的优点是:新颖、灵活、画面鲜艳美丽。教材内容具有综合性,能给教师以广阔、自由的空间,这就要求教师对教材用心领悟,深入挖掘,创造性地处理和使用,把教材激活,提升学生的思维深度。整个学习过程,学生的兴趣会更浓厚,对于小数乘整数、积的小数位数与因数的小数位数之间的关系也会掌握得更好。
在教学过程中,如果教师能在实施预设时不拘泥于预设,能处理好预设与生成的关系,充分利用课堂上的生成资源,满足学生探求的欲望,那么枯燥的数学课将变得魅力无限。
(作者单位:江苏省太仓市朱棣文小学)endprint

