基于LiDAR点云的高精度DEM构建方法
于彩霞,董 箭,李改肖,陈惠荣,王 沫1,
(1.信息工程大学 地理空间信息学院,河南 郑州450052;2.地理信息工程国家重点实验室,陕西 西安710054;3.海军大连舰艇学院,辽宁 大连 116018)
基于LiDAR点云的高精度DEM构建方法
于彩霞1,2,3,董 箭3,李改肖3,陈惠荣3,王 沫1,3
(1.信息工程大学 地理空间信息学院,河南 郑州450052;2.地理信息工程国家重点实验室,陕西 西安710054;3.海军大连舰艇学院,辽宁 大连 116018)

对激光雷达测量点云滤波分类出真实地面点,通过不同的方法构建高精度的数字高程模型,包括不规则三角网模型和Grid模型,采用等值线回放法和检查点法分别从定性和定量角度评估DEM的精度。实验表明,线性三角网插值法构建的DEM边界约束最好、精度较高,且效率最高,是LiDAR点云构建高精度DEM的最优方法。
LiDAR;高精度;DEM;等值线;精度评估
LiDAR能够快速获取高精度、高密度的三维地形数据[1],成为构建高精度DEM的一种新方法。目前从LiDAR数据中构建DEM的方法研究较少[2,3],主要从工程应用角度对如何通过LiDAR数据生产DEM进行探讨,缺少对不同DEM构建模型的适用性研究,以及对其构建的DEM进行精度评估。
针对上述问题,本文将基于高密度、高精度的海量LiDAR点云,采用不同模型构建DEM,通过对LiDAR点云数据进行实验,分别从定性和定量的角度出发,对DEM构建算法进行精度评估,以期为海量的高密度点云构建DEM的模型选择提供一定的参考,同时也为后续的LiDAR点云数据处理和应用打下基础。
1 DEM的构建与精度评估
1.1 DEM构建方法
基于LiDAR点云的高精度DEM构建,首先需对LiDAR点云进行粗差滤波处理,滤除粗差数据并保留真实的地面点云;然后通过不同的DEM构建算法由地面真实点云生成DEM,其中包括不规则TIN和规则格网Grid;最后采用等值线回放法和检查点法分别从定性和定量出发评估DEM精度。流程如图1所示。
1)LiDAR点云处理。在本文中LiDAR预处理包括2部分工作:①LiDAR原始点云的粗差(噪声)去除。LiDAR点云在获取时随机性大,易受到外界因素的影响,以及激光脉冲的散射和衍射现象等问题,不可避免地给最终的测量结果带来粗差和噪声[4]。这些粗差和噪声包括高点、低点及孤立点/点云等3类[5],必须剔除处理,否则会造成局部地形的变形甚至失真,严重影响DEM的精度。②点云的滤波分类。LiDAR点云的滤波分类实质是去除点云中的非地面点,保留真实地面点云。滤波方法有很多[1,6],较为成熟的是Axelsson提出的基于TIN的渐进加密滤波法。本文将采用该方法对LiDAR点云滤波,并通过实验不断调整阈值以得到更为真实的地面点云[7]。
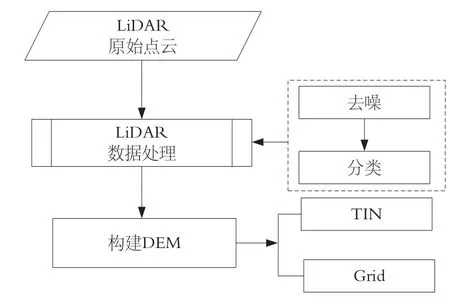
图1 基于LiDAR点云的DEM构建示意图
2)DEM构建模型。DEM有多种表达方法,目前常用的主要有不规则三角网(TIN)模型和规则格网(Grid)模型[8,9]。①TIN模型。采用TIN对LiDAR数据进行建模,相互连接LiDAR原始点云生成三角形。连接点云时需满足选择最近的点形成三角形,生成的三角形唯一、不交叉、不重叠以及尽量接近正三角形等原则[8,9]。② Grid模型。Grid是用一系列规则格网表示地形表面,主要有反距离加权插值法(IDW)、克里金(Kriging)插值法、线性三角网插值法(TLI)和最近邻点插值法(NN)[8-11]等。其中,反距离加权插值法的基本原理是己知点云的坐标和高程,通过加权计算格网点的高程值,离格网距离越近的点云,权重越大。克里金插值法考虑到空间场的各向异性和LiDAR点云的空间相关性,应用数学模型和统计模型确定对格网有影响的距离范围,并内插得格网的高程。线性三角网插值法通过连接点云构建三角网,根据三角网内的点云均匀分配格网的属性值,属于严密的插值方式。最近邻点插值法是指选择离格网最近的点云作为格网的属性值。
1.2 DEM精度评估
本文采用等值线回放法和检查点法来评估基于LiDAR点云构建的DEM精度。
等值线回放法是将构建的DEM内插生成等值线,然后目视检查,并与其他方法生成的等值线进行比较,属于定性评估。检查点法是选择并预留一定数量的分布均匀、合理的LiDAR点为检查点,其高程为Zi(i=1,2,…,n),由构建的DEM内插出这些点的高程值Zi',则DEM的精度为:

2 实验与分析
实验区域位于大连某海岸,属于地形陡峭的岩石陡岸。LiDAR数据由中海达激光扫描仪iScan采集,点云间距为0.1 m,点云总量为22.6万。
先对LiDAR去除粗差,并滤波分类出真实地面点云,然后根据不同方法构建TIN模型和Grid模型,分别从定性和定量角度评估其构建的DEM精度。
2.1 定性分析
由TIN模型内插的等值线如图2所示,由TIN生成的等值线破碎、曲折多、抖动大;由Grid生成的等值线(如图3~6所示)较为平滑、合理,这是因为LiDAR点云的高频噪声引起了等值线的曲折抖动[10],而构建Grid模型的过程则是通过一定的插值算法将LiDAR点云的高程均衡化的过程,从一定程度上滤掉了高频噪声,抑制了高频噪声的影响。
根据反距离加权插值法、克里金插值法、线性三角网插值法和最近邻点插值法分别生成不同分辨率的Grid(分辨率分别为0.5 m和1 m),插值得等值线分别如图3~6所示。高分辨率(0.5 m)的Grid模型对地形表面描述更为细致,由其生成的等值线弯曲稍多。随着分辨率的降低(分辨率为1 m时),Grid模型对地表描述较为粗略,由其生成的等值线较为平滑。从整体上看,这4种不同插值方法构建的DEM及生成的等值线差别不大,但由线性三角网插值法构建的DEM边界约束较好(见图5),其他3种方法还需在边界约束问题上进行改进。

图2 基于TIN生成等值线

图3 基于反距离加权插值法的Grid生成等值线

图4 基于克里金插值法的Grid生成等值线

图5 基于线性三角网内插法的Grid生成等值线
2.2 定量分析
根据式(1)计算Grid的精度,同时记录不同方法构建Grid的时间,如表1所示。实验表明:①Grid分辨率与插值方法的精度成正比,与插值方法的时间成反比。②各类插值方法的插值精度波动不大,均介于1~2倍的Grid分辨率之间。③相对于线性三角网插值法与最近邻点插值法,反距离加权插值法与克里金插值法具有相对较高的插值精度,然而插值效率却严重低下。这主要由于在应用反距离加权插值法与克里金插值法进行Grid插值时,需要搜索格网点周围一定数量的离散点来确定格网点高程值。在没有建立有效空间索引的前提下,会造成搜索效率的严重低下,这对于处理数据量较大甚至海量数据的LiDAR点云显然并不适合。④线性三角网插值法的插值精度优于最近邻点插值法,且插值效率的变化较为均匀。基于上述分析不难看出,线性三角网插值法在处理大数据量的LiDAR点云数据时,插值精度与插值效率均相对优于其余三类插值方法,可作为LiDAR点云数据插值的优选方法。
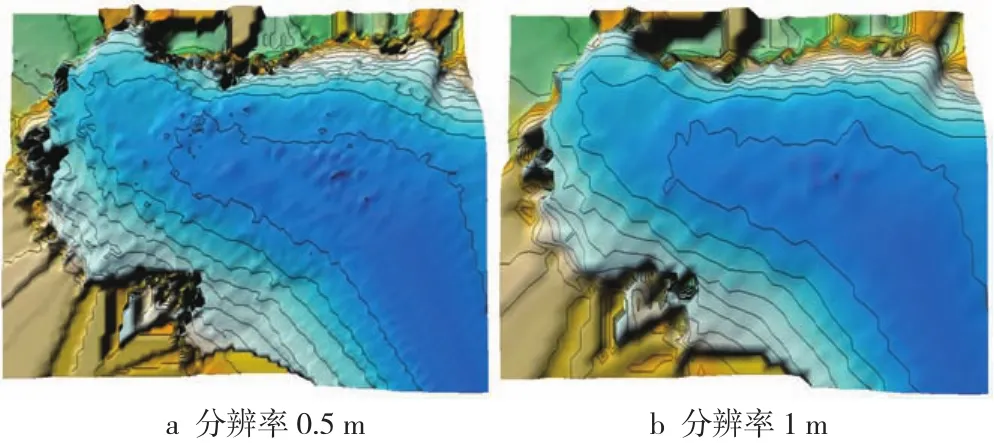
图6 基于最近邻点插值法的Grid生成等值线
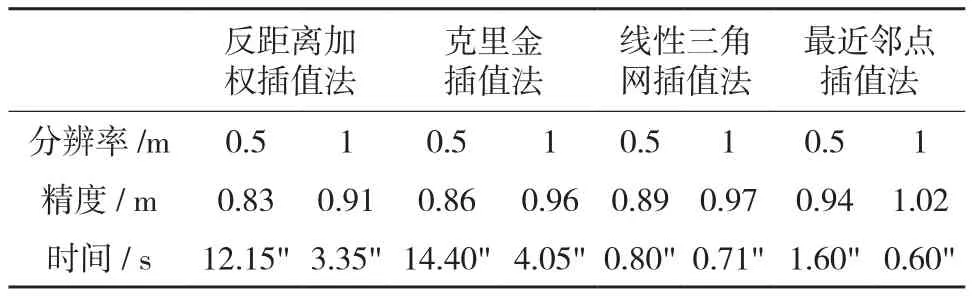
表1 构建Grid不同插值方法的比较
3 结 语
本文针对LiDAR点云数据,利用不同的DEM构建方法生成不同分辨率下的DEM,并分析了DEM的构建精度和效率。实验结果表明:DEM的精度主要取决于采样间隔和地形的复杂程度,不同的插值方法在处理高密度、高精度的海量LiDAR点云时,所得DEM的精度相差不大,但其构建效率却存在较大变化。线性三角网插值法构建的DEM精度较高,所用时间较短且变化均匀,是LiDAR点云构建DEM的较好方法。
鉴于数据缺少原因,本文仅针对复杂的岩石陡岸(属于中度复杂地貌)进行了实验分析,下一步将结合不同类型、不同复杂程度的地形地貌研究DEM构建方法的适用性,并将结合地性线的提取(如山脊线、骨架线等)进一步提高DEM精度。
[1] 张小红. 机载激光雷达测量技术理论与方法[M].武汉:武汉大学出版社,2007
[2] 王铁军,陈云,袁如金. 基于LiDAR数据的DEM和矢量自动提取探讨[J]. 测绘与空间地理信息,2009,32(1):29-31
[3] 李晓红. 一种LiDAR点云生成格网DEM的快速算法[J]. 测绘通报,2012(12):44-46
[4] 王永波. 基于地面LiDAR点云的空间对象表面重建及多分辨率表达[M].南京:东南大学出版社,2011
[5] Zhang L, Ma H C, Wu J W. Utilization of LiDAR and Tidal Gauge Data for Automatic Extracting High and Low Tide Lines[J]. Journal of Remote Sensing, 2012,16(2):405-410
[6] 王金亮,陈联君.激光雷达点云数据的滤波算法述评[J].遥感技术与应用,2010, 25(5):632-638
[7] Axelsson P. DEM Generation form Laser Scanner Data Using Adaptive TIN Models [J]. IAPRS, 2000, 33(B4 ):110-117
[8] 张君. 不同算法下生成的数字高程模型对比分析研究[J]. 计算机应用与软件,2009,26(1):88-90
[9] Johns K H. A Comparison of Algorithms Used to Compute Hill Slope as a Property of the DEM [J]. Computer and Geoscience, 1998, 24(4):315-323
[10] 李志林,朱庆.数字高程模型[M].武汉:武汉大学出版社,2012
[11] 陈欢欢,李星,丁文秀. Surfer 8.0 等值线绘制中的十二种插值方法[J]. 工程地球物理学报,2007,4(1):52-57
[12] 范青松,汤翠莲,胡鹏. DEM精度检查中等高线回放的量化方法[J]. 测绘科学,2008, 33(3):118-120
[13] 王光霞,边淑莉,张寅宝. 用回放等高线评估DEM精度的研究[J]. 测绘科学技术学报,2010,27(1):9-13
P237.9
B
1672-4623(2015)03-0022-03
10.3969/j.issn.1672-4623.2015.03.008
于彩霞,博士,讲师,主要从事海洋地理信息系统数据处理研究。
2015-02-09。
项目来源:国家自然基金资助项目(41171349);地理信息工程国家重点实验室开放研究基金资助项目(SKLGIE2014-M-3-2);海军大连舰艇学院2110工程三期资助学术预研课题资助项目(DLJY—XY2014016)。

