极端死亡率债券的运行机制与定价模型

谢世清+周庆余

摘 要：极端死亡率债券是票息或面值与极端死亡概率相关的债券，能够将寿险公司所面临的极端死亡率风险转移到资本市场。本文阐述了极端死亡率债券的市场发展，包括发行规模、触发机制、债券期限、债券分层、债券评级等，分析了以Tartan债券为代表的本金赔付累积型极端死亡率债券的运行机制，并给出了考虑极端死亡率风险的跳跃性特征下的本金赔付累积型极端死亡率债券Wang转换定价的解析式。

关键词： 极端死亡率债券;运行机制;市场发展;定价模型

中图分类号：F840.0   文献标识码： A    文章编号：1003-7217（2015）01-0029-05

一、引 言

极端死亡率风险源于寿险公司所面临的实际死亡率远高于其承保时所预测的数值。近年来，巨灾事件和流行病事件频繁发生，导致寿险公司面临着日益严峻的极端死亡率风险。极端死亡率风险使得寿险公司可能在一次事故中支付众多被保险人的死亡赔偿金，造成寿险公司严重亏损，甚至因现金流不足而遭遇清算倒闭的危机。巨灾频发、流行病肆虐以及恐怖袭击等潜在威胁，未来极端死亡率风险有可能会进一步恶化，寿险公司需采用有效的风险管理方法来减少极端死亡率风险造成的损害。

寿险公司通常采用四类传统方法应对极端死亡率风险，包括经济资本吸收实际损失、出售大量保单分散风险、提高保单费率转嫁风险以及通过再保险转移风险。但这些传统方法均存在一定的局限性。为更好地应对极端死亡率风险，2003年，瑞士再保险（Swiss Re）首次将产险证券化方法应用于寿险风险，成功地发行了以寿险保单死亡率为标的指数的极端死亡率债券。同巨灾债券类似，极端死亡率债券能够将传统保险业的死亡率峰值风险转移或分散到资本市场。

目前，国外学者对极端死亡率债券的研究主要集中于两个方面：首先，在运行机制方面，Blake et al.（2006）等对瑞士再保险发行的Vita系列债券进行了研究^[1];Bauer and Kramer（2007）探讨了苏格兰再保险发行的Tartan系列债券^[2]。其次，定价模型方面，Wang（2000）提出的Wang转换方法，实现了不完全市场中的死亡率风险定价^[3];Chen and Cox（2009）应用风险中性定价方法对极端死亡率债券进行了定价^[4]。我国尚勤等（2010）对死亡率债券进行了Wang转换定价^[5]。本文旨在对极端死亡率债券的运行机制和定价模型进行分析，以弥补国内在这一领域研究的缺失。

二、极端死亡率债券的市场发展

2003～2012年，全球共成功发行了9次极端死亡率债券（见表1）。瑞士再保险是极端死亡率债券最为重要的发起人。在9次发行中，由瑞士再保险发行的共有6次。迄今为止，Vita系列债券共为瑞士再保险筹集了20.5亿美元，凸显了其在资本市场上较强的品牌效应。这些债券的成功发行探索出了一条转移极端死亡率风险的新渠道，激发了寿险行业和固定收益证券相结合的热情。随后，苏格兰再保险、安盛保险（AXA）和慕尼黑再保险也纷纷效仿并发行了各自的极端死亡率债券。

1.发行规模。如表1所示，2006～2007年全球共发行了四次极端死亡率债券，从资本市场上筹集到了大约11.6亿美元的资金，每次平均融资额约为3亿美元。受国际金融危机的影响，极端死亡率证券化产品的发行在此后三年内陷入了相对低迷的时期，直到2010年10月之后，极端死亡率债券的发行才开始了新一波行情，共成功发行三次，融资总额为9.6亿美元。目前整个资本市场通过极端死亡率债券所提供的资金总额仍不足此类风险敞口的10%，因此，极端死亡率债券未来将拥有巨大的市场发展潜力。

财经理论与实践（双月刊）2015年第1期2015年第1期（总第193期）谢世清，周庆余：极端死亡率债券的运行机制与定价模型

2.触发机制。

极端死亡率债券的触发条件一般基于公开的死亡率指数，即基于不同国家、年龄和性别等构造的“组合死亡率指数”。例如，Vita I债券触发机制是基于美国、英国、法国、意大利和瑞士这5个国家的死亡率构建的加权死亡率指数。如果仅使用单个国家的死亡率作为参照标准，缺乏人口和地理位置上的多样性，容易产生非系统风险。而对于资产规模大、多个地区经营的发起寿险公司或再保险公司而言，不同国家和地区的“组合死亡率指数”更能贴近其极端死亡率暴露情况，因而能够有效减少其“基差”风险。

3.债券期限。已发行的极端死亡率债券的期限通常为3～5年，属于中期债券。如果债券期限过长，会导致阈值触发的概率偏高，投资者面临的风险加大，债券吸引力减小。此外，债券的实际期限也会由于具有延期性和赎回性而有所改变。首先，债券本金的偿付需根据死亡率指数水平来确定，而债券到期后往往需要一定时间来收集死亡率数据和计算出死亡率指数;其次，债券实际期限会因债券无法对冲发行人所实际承担的极端死亡率风险或者发行人能够重新发行息票率更低的债券而被提前赎回。

4.债券层级。最初的Vita I债券是不分层级的债券，但从Vita II开始，极端死亡率债券也引入了债券的分层设计。分层的方式主要有两种：一是根据不同的人口特征或地理位置进行分层;二是根据不同的期限、触发阈值和资金规模等进行分层。发起人还能通过自身购买风险最高的“权益层”债券实现风险自留，对道德风险进行有效控制，以提升其他层级债券的信用等级。债券的分层可以实现风险配置的多样性，满足市场风险偏好不同的投资者的需求，拓展市场容量，提高市场流动性。

5.债券评级。

与资产证券化产品类似，极端死亡率债券的发行通常要经过权威评级机构如标准普尔的信用评级。评级考虑的因素包括债券层级、触发阈值和到期时间等。已发行的极端死亡率债券的信用级别通常集中于BBB-～BB+，大部分属于投机级别。债券评级与债券息差紧密相关。评级为BBB级别债券的息差比AAA级别债券的息差平均高出1%左右，有时甚至超过3%。此外，投机级别债券比投资级别债券在息差上平均高出4%左右，有时超过6%。例如，2009年，在甲型H1N1流感的影响下两者的息差甚至超过15%。

三、 极端死亡率债券的运行机制

自2003年瑞士再保险发行Vita债券以来，极端死亡率债券的市场已取得了长足的发展。迄今为止全球已经发行了9笔极端死亡率债券，发行总金额为26亿美元。Vita系列债券属于本金赔付非累积型债券，每年从SPV中提取的资金以及提取的比例均逐年重新计算，与往年的累积本金赔付比例无关。2006年苏格兰再保险发行的Tartan系列极端死亡率债券通过设计双重触发条件妥善地解决了死亡率时序相关的问题，其偿付机制更具合理性。有鉴于此，这里选取Tartan债券作为典型案例来剖析极端死亡率债券的交易结构和偿付机制。

（一）极端死亡率债券的交易结构

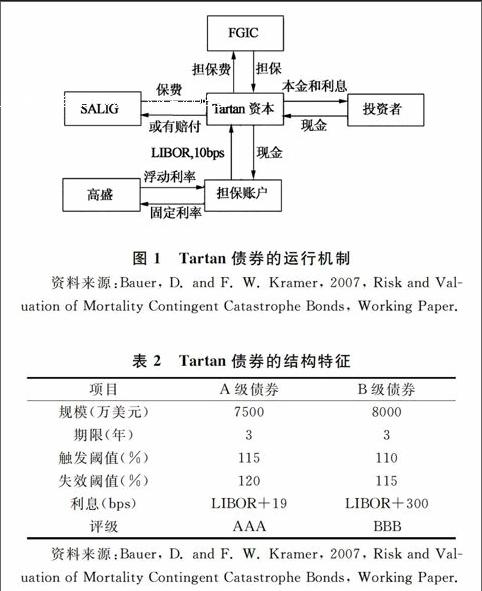
Tartan债券的交易结构如图1所示。首先，隶属于苏格兰再保险的苏格兰年金与寿险公司（SALIC）同特殊目的公司（SPV）Tartan资本签订了再保险合约。在该合约下，SALIC同意每季度支付Tartan资本一个固定的金额作为保费，以换取当死亡率指数达到一定的阀值时Tartan资本向SALIC支付赔偿的权利。其次，Tartan资本通过向资本市场投资人发行极端死亡率债券能够为其向SALIC的或有支付筹集资金。再次，发行债券所募集的资金用以购买无风险的国债存入担保账户作为抵押资产。最后，鉴于这些抵押资产收益较低，Tartan资本将会和高盛签订利率互换合约。

Tartan资本共发售2个不同风险暴露的Tartan债券：面值分别为7500万美元和8000万美元，期限均为3年。表2列出了Tartan债券的具体结构特征。其中，A级债券的本金和利息均由担保公司（FGIC）进行担保，相应地，FGIC会从Tartan资本收取一定的担保费。因此，对于A级债券投资者来说，其仅面临信用风险，相应的利息收益也较低，只有LIBOR+19基点。而B级债券投资者将会面临较高的极端死亡率风险，当风险事件发生时债券投资人将会损失利息和本金。作为风险补偿，其收益也较高，利息比A级债券高出281基点。

（二）极端死亡率债券的偿付机制

如果事先约定的死亡率指数超过一定的阈值水平，Tartan资本动用存放在担保账户中的抵押资产对SALIC进行赔偿支付。该死亡率指数为联合死亡率指数（combined mortality index，CMI），会随着既定人口的死亡率变化。之所以设定CMI，而不是选取特定人群的死亡率作为死亡率指数，是为了充分反映SALIC面临的不同年龄、不同性别人群的极端死亡率风险。CMI仅以美国人口死亡率作为依据。美国人口死亡率是指在下一年中由美国疾病控制和防御中心公布的整体人口数量减少的一定比例。CMI是一个加权的人口死亡率t：

t=∑xωx，mm，x，t+ωx，ff，x，t（1）

其中，m，x，t和f，x，t分别为t年，年龄组x中男性和女性的死亡率;ωx，m和ωx，f分别为这两个死亡率所对应的权重。

Tartan债券中，假设t和t-1分别为t年和t-1年的加权人口死亡率，2004和2005为基年的死亡率指数，则t年的实际死亡率指数it可由下式计算得到：

it=1/2t+t-11/22004+2005（2）

从式（2）不难看出，联合死亡率指数依赖于连续两年的人口死亡状况，而Tartan债券为3年期的债券，因此，只在两个时点上才会计算死亡率指数及其相连的本金赔付损失，即通过2006和2007年的数据计算2007年年末的死亡率指数，通过2007和2008年的数据计算2008年年末的死亡率指数。然而，由于计算死亡率指数的数据通常在年末是不可得的，因此，Tartan债券有可能会将债券期限最多延长30个月。但是债券在延展期间并不会因为极端死亡率事件而遭受任何本金损失，并且投资人依旧会获得延展期间的利息收入。

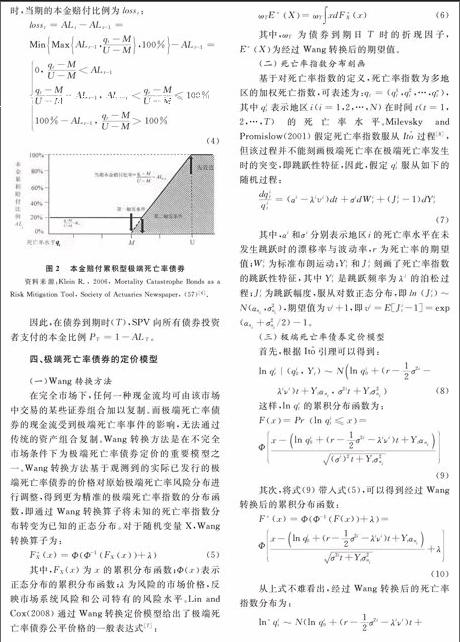
Tartan债券还规定只有在死亡率指数超过一定的水平时，寿险公司才会接受赔偿。如图2所示，黑色的实线为每期的累积本金赔付比例与当期的死亡率水平的关系。第一个触发条件与Vita债券的偿付机制相同，即死亡率指数超过基准水平的下限（M）;第二个触发条件为本期的本金赔付比例大于以往各年的本金赔付比例之和，即超过累积本金赔付比例（Accumulated Loss，ALt-1），即只有当期的赔付比例超过上一期的累计比例阈值ALt-1，SPV才进行本金赔付。用公式表示，在t时期SPV向寿险公司的累积本金偿付比例为ALt：

ALt=MinMaxALt-1，qt-MU-M，100%（3）

当上一期的累积本金赔付比例尚未达到100%时，当期的本金赔付比例为losst：

losst=ALt-ALt-1=

MinMaxALt-1，qt-MU-M，100%-ALt-1=

0，                               qt-MU-M

qt-MU-M-ALt-1，         ALt-1

100%-ALt-1，            qt-MU-M>100%（4）

图2 本金赔付累积型极端死亡率债券

资料来源：Klein R.， 2006， Mortality Catastrophe Bonds as a Risk Mitigation Tool， Society of Actuaries Newspaper， （57）^[6].

因此，在债券到期时（T），SPV向所有债券投资者支付的本金比例PT=1-ALT。

四、极端死亡率债券的定价模型 （一）Wang转换方法

在完全市场下，任何一种现金流均可由该市场中交易的某些证券组合加以复制。而极端死亡率债券的现金流受到极端死亡率事件的影响，无法通过传统的资产组合复制。Wang转换方法是在不完全市场条件下为极端死亡率债券定价的重要模型之一。Wang转换方法基于观测到的实际已发行的极端死亡率债券的价格对原始极端死亡率风险分布进行调整，得到更为精准的极端死亡率指数的分布函数，即通过Wang转换算子将未知的死亡率指数分布转变为已知的正态分布。对于随机变量X，Wang转换算子为：

F*X（x）=ΦΦ-1FXx+λ（5）

其中，FX（x）为x的累积分布函数;Φx表示正态分布的累积分布函数;λ为风险的市场价格，反映市场系统风险和公司特有的风险水平。Lin and Cox（2008）通过Wang转换定价模型给出了极端死亡率债券公平价格的一般表达式^[7]：

ωTE*X=ωT∫xdF*X（x） （6）

其中，ωT为债券到期日T时的折现因子，E*X为经过Wang转换后的期望值。

（二）死亡率指数分布刻画

基于对死亡率指数的定义，死亡率指数为多地区的加权死亡指数，可表述为：qt=（q1t，q2t，…，qnt），其中qit表示地区i（i=1，2，…，N）在时间t（t=1，2，…，T）的死亡率水平。Milevsky and Promislow（2001）假定死亡率指数服从It过程^[8]，但该过程并不能刻画极端死亡率在极端死亡率发生时的突变，即跳跃性特征，因此，假定

qit服从如下的随机过程：

dqitqit=（αi-λivi）dt+σidWit+（Jit-1）dYit（7）

其中，αi和σi分别表示地区i的死亡率水平在未发生跳跃时的漂移率与波动率，r为死亡率的期望值;Wit为标准布朗运动;Yit和Jit刻画了死亡率指数的跳跃性特征，其中Yit是跳跃频率为λi的泊松过程;Jit为跳跃幅度，服从对数正态分布，即ln （Jit）～N（αni，σ2ni），期望值为vi+1，即

vi=E[Jit-1]=exp （αni+σ2ni/2）-1。

（三）极端死亡率债券定价模型

首先，根据It引理可以得到：

ln qit|（qi0， Yt）～Nln qi0+（r-12σ2i-

λiνi）t+Ytαni， σ2it+Ytσ2ni

（8）

这样，ln qit的累积分布函数为：

Fx=Pr ln qit≤x=

Φx-ln qi0+（r-12σ2i-λiνi）t+Ytαni（σi）2t+Ytσ2ni（9）

其次，将式（9）带入式（5），可以得到经过Wang转换后的累积分布函数：

F*（x）=ΦΦ-1F（x）+λ=

Φx-ln qi0+（r-12σ2i-λiνi）t+Ytαniσ2it+Ytσ2ni+λ（10）

从上式不难看出，经过Wang转换后的死亡率指数分布为：

ln*qit～N（ln qi0+（r-12σ2i-λiνi）t+

Ytαni-λσ2it+Ytσ2ni， σ2it+Ytσ2ni）（11）

进一步进行对数变换即可得到死亡率指数qit经过风险调整后的期望值为：

E*qit=expln qi0+（r-12σ2i-λiνi）t+

Ytαni-λσ2it+Ytσ2ni+12σ2it+Ytσ2ni

（12）

最后，基于苏格兰再保险发行的Tartan系列极端死亡率债券的偿付机制，得出本金赔付累积型极端死亡率债券的定价解析式。由于通过Wang转换得到的价格为公平价格，因此，式（6）中折现因子ωT应为无风险利率下连续复利的折现因子e-rT;债券的到期价值为V=Par1-∫T1losstdt，Par为债券的面值。将折现因子和债券的到期价值以及经过风险调整后的死亡率指数期望值E*qit带入式（6）即可得到极端死亡率债券的最终价格：

P=e-rTE*Par1-∫T1losstdt=

e-rTPar1-∫T1E*qit-MU-M-ALt-1dt

（13）

相较于通过完全市场方法对极端死亡率债券定价，使用Wang转换对极端死亡率债券进行定价会得到更为精准的债券价格。该模型的优点是将风险溢价计入到期望损失中，在一定程度上反映了死亡率风险的厚尾性特征。但该模型却要求死亡率指数的概率分布已知，而通常情况下死亡率指数的分布函数是未知的，只能通过死亡率样本进行概率分布函数参数的估计。

五、结 语

极端死亡率债券是极端死亡率风险证券化的重要产物，也是国际上应对极端死亡率风险不可或缺的创新性管理工具。本文的研究发现，本金赔付非累积型和累积型两类极端死亡率债券在运行机制上存在较大的差异。其中，本金赔付累积型极端死亡率债券由于门阀值与累积损失相关，因此触发条件更为苛刻。由于后者在更大程度上保护了投资者的利益，因而更加受到市场欢迎。目前，国内学术界对于极端死亡率债券的研究较少，本文系统梳理了极端死亡率债券的运行机制和定价模型，期盼能够引起我国学术界和业界对极端死亡率债券的关注。

参考文献：

[1]Blake， D.， A.J.G. Cairns， and K. Dowd. Living with mortality： longevity bonds and other mortalitylinked securities [J]. British Actuarial Journal， 2006， 12（1）： 153-197.

[2]Bauer， D. and F. W. Kramer. Risk and valuation of mortality contingent catastrophe bonds[R]. Working Paper， 2007.

[3]Wang， S.. A class of distortion operations for pricing financial and insurance risks [J]. Journal of Risk and Insurance， 2000， 67（1）： 15-36.

[4]Chen， H. and S. H. Cox. Modeling mortality with jumps：application to mortality securitization [J]. Journal of Risk and Insurance， 2009， 76（3）： 727-751.

[5]尚勤， 秦学志， 周颖颖. 巨灾死亡率债券定价模型研究 [J]. 系统工程， 2010，（2）：203-208.

[6]Klein， R. Mortality catastrophe bonds as a risk mitigation tool[M]. Society of Actuaries Newspaper，2006.

[7]Lin， Y. and S.H. Cox. Securitization of catastrophe mortality risks [J]. Insurance： Mathematics and Economics， 2008，（42）：628-637.

[8]Milevsky， M. A. and S. D. Promislow. mortality derivatives and the option to annualize [J]. Insurance： Mathematics and Economics， 2001， 29 （3）： 299-318.

（责任编辑：宁晓青）

The Operational Mechanism and Pricing

Model of Extreme Mortality Bonds

XIE Shiqing， ZHOU Qingyu

（School of Economics， Peking University， Beijing 100871，China）

Abstract：Extreme mortality bonds （EMBs） refer to the bonds whose principals vary with mortality index due to the extreme mortality risk. This paper presents the EMB market development from the perspectives of issue scale， trigger mechanism， bond maturity， tranche and bond rating; analyzes the payment mechanism of cumulative principal of the EMBs based on the Tartan bond issued by Scottish Re in 2006; derives an analytical formula of pricing the EMBs based on a single factor Wang transfer method considering the jump diffusion of mortality risk.

Key words：Extreme mortality bond; Operating mechanism; Market development; Pricing model