基于矩阵的apriori算法的改进

张卫华

（江苏大学 计算机科学与通信工程学院，江苏 镇江 212013）

关联规则挖掘是数据挖掘中的一个重要的问题。而apriori算法是挖掘关联规则的经典算法。主要步骤是：通过扫描数据库得到频繁1-项集，然后频繁1-项集组合候选2-项集，然后对候选项2-项集剪枝，通过扫描数据库得到支持度计数来生成频繁2-项集。以此类推，直到没有频繁项集产生，然后将频繁项集生成关联规则[1]。这样一来，这个算法中有两个重要的问题：大量的候选项集产生和多次扫描数据库。

针对以上两个问题，文献 [6]中使用的是基于矩阵的apriori算法,此算法将事务集以矩阵的形式保存到内存中，通过计算矩阵列向量中1出现的个数然后与最小支持度计数比较从而得到频繁1-项集，在产生频繁k-项集的时候(k>1),首先对频繁k-1-项集进行连接后得到候选k-项集，将对应的k个矩阵列进行位与运算生成列向量，计算列向量中1出现的个数，与最小支持度计数比较判断而产生频繁项集，此算法只需要扫描一次数据库，而且通过减少无用连接而减少了候选项集的产生。文献[2]、[7]采取的是直接产生频繁项集,从而减少了连接和剪枝时间，即直接按顺序对矩阵k个列进行位与运算得到列向量，对列向量1出现的个数进行计数然后和最小支持度计数比较产生频繁k-项集，此算法通过删减矩阵的列来减少位与运算的次数，而删减列前需要对频繁k-1-项集的查找，即判断频繁项集中的项Ij在所有频繁k-1-项集中出现的次数是否小于k-1，然后再删除此项对应对应的矩阵列。文献[3]、[4]、[5]采取的方法是通过查找每一个频繁k-1-项集而得出此项在所有的频繁k-1-项集中出现次数，然后再判断是否需要删除此项所对应的矩阵列，这样会导致多余的扫描。因此本文针对此问题提出一种新的查找方法，利用频繁项集的有序性，不一定要查找所有的频繁k-1-项集，利用矩阵的删除性质，并不要得出每一项的在频繁k-1-项集的计数,而是一旦发现在频繁k-1的计数等于k-1则进入下一个项的计数，从而节约了时间。将这种查找方法应用到的基于矩阵的apriori算法[2，7]中,从而降低了整个算法的时间复杂度。

1 改进的查找方法

1.1 删减矩阵的相关性质

性质1如果某列的1出现的个数小于最小支持度计数，则删除此列。

性质2如果在产生频繁k-项集之前，对布尔矩阵扫描发现，某事务行的1出现的个数少于k，则删除此事务。

性质3在布尔矩阵中，在产生频繁k-项集之前，如果某数据项Xi在所有的频繁k-1-项集中出现的次数少于k-1次，那么此数据项Xi参与组合成的所有候选k-项集如{X1,X2,X3,Xi,....Xk}必不是频繁项集，则可以删除此数据项[9]。

证明：反证法。如果候选k-项集{X1,X2,X3,Xi,....Xk}是频繁项集，则元素Xi参与组成的k-1子集的个数就是 ，即k-1，那么元素Xi在频繁k-1-项集中出现的次数大于等于k-1，与条件矛盾，证明完毕。

1.2 项集的有序性

apriori算法中产生的频繁项集的项是按字典序存储的，即频繁k-1-项集的前面一项的字典序不得大于后一项的字典序。如项A、B、C、D、E按字典序依次排列。那么在项集ABCD是允许的，而ABDC是不允许的，因为C的字典序比D小。

1.3 改进的查找方法

在性质3中，需要对频繁k-1-项集进行查找。常见的方法，使用for循环按行查找项在所有的频繁k-1-项集[3-5，7]出现的次数，通过判断次数是否小于k-1来决定是否删除项，伪代码如下。

For each item I Lk-1

For each iK //K是出现在所有频繁k-1-项集中项的集合

If iI

I.count++;

For each i K

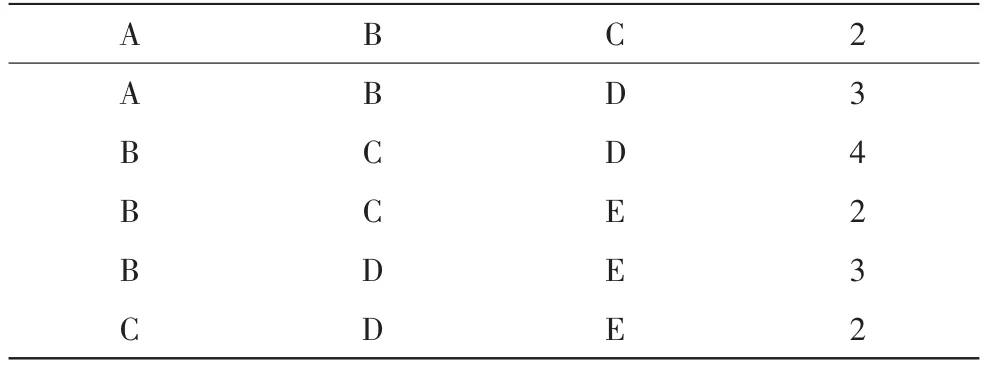
If i.count

For each item I Lk-1

If iI

Delete I

这样忽略了项集的有序性，不一定要查找每一个频繁k-1-项集，此外利用矩阵的删除性质3，并不要得出每一项的在频繁k-1-项集的计数，而是找出在频繁k-1-项集中出现次数少于k-1的项Xi即可。

针对以上问题，提出一种改进的查找方法即，将频繁k-1-项集的下标组合按行存储在二维数组中[8]，最后一列是它的计数。

第一，按行对频繁k-1-项集进行搜索，如果发现某一项Xi在频繁k-1-项集中出现的次数已经等于k-1，立即放弃扫描，跳到下一个项的计数。如在扫描B时候，发现扫描第三行就发现B的计数就为3，则停止扫描，进入对C的计数。

第二，利用频繁项集的有序性[2]，减少扫描量。即按行搜索项Xi在频繁k-1-项集的次数的时候，若是第一列出现的项的字典序大于Xi的字典序，则停止搜索，因为接下来的矩阵行中不可能还出现Xi，由于第一种改进的存在，所以这项在频繁k-1-项集出现的次数就是小于k-1，删除此项。如下面表1，表2。搜索A时候，在第三行中第一列出现了B，则停止搜索，后面的频繁3-项集不可能还出现A，A项在频繁k-1-项集中出现的次数必然是小于3，所以删除此项。

表1 事务集Tab.1 Transaction set

伪代码如下：

For item i Lk-1 {

For j //j是矩阵的行

{

}

If A[j][0]]>L[i]; //如果行的第一列的字典序大于搜索项的字典序

{

Delete i;

Step to next i； //进入下一项的扫描；

For k //k是矩阵的列

{

If A[j][k]==i

i.count++;

If i.count==k-1

Step to next i；

}

}

}

表2 存入数组中烦人频繁3-项集Tab.2 Frequent 3-set stored in array

2 算法的设计和说明

2.1 算法的基本思想

算法通过将事务映射成一个矩阵，然后通过矩阵中的数据项列向量进行位与运算，然后对其计数向量中的1出现的总和，然后与最小支持度计数比较直接产生频繁项集[7]。这个过程中不产生候选项集，但是会通过改进的查找方法进行删减矩阵列来减少矩阵列参与位与运算的次数，此外会通过删减矩阵行减少对矩阵的扫描量和内存消耗。

2.2 算法的主要步骤

第一步：建立矩阵。将事务映射成矩阵，矩阵一行对应一条事务。其中项出现的为1，不出现的为0。

第二步：产生频繁1-项集和频繁2-项集。产生频繁项集1后，应用性质1，性质2对矩阵进行压缩。然后在这个基础上产生频繁2-项集。

第三步：删减矩阵。

对行的删除：应用性质2，如果矩阵行中1出现的次数,少于k，则删除此事务行。

对列的删除：应用性质3，用改进的查找方法找出在频繁k-1-项集中出现的次数小于k-1的项Xi，然后删掉。

第四步：产生频繁k项集（k>3）。将矩阵行k（k>1）个行向量相与，计算行中各个1的和,然后将这个和与最小支持度计数相比较，如果大于等于，则这几个数据项的组合就是频繁项集。然后将组合的数据项列号和频数用二维数组存储起来，便于第三步中进行查找。

第五步：不断重复第三步，第四步，到无法产生频繁项集。

3 算法的示例

第一步：将矩阵映射为矩阵，如表4。

第二步：产生频繁1-项集和频繁2-项集。假定最小支持度计数为2，A的向量形式为{A：101110}，对出现的 1个数求和，支持度计数为4，所以A保留，依此得到频繁1-项集为：{A}，{B}，{C}，{D}，{E}。 将矩阵列 A 和 B 进行位相与，得到{AB：101010}，支持度计数为3，所以为频繁项集。这样得到频繁2-项集为：

表3 事务集tab.3 Transaction set

表4 对应的矩阵Tab.4 The corresponding matrix

{AB},{AC},{AD},{AE},{BC},{BD},{BE},{CD},{CE},{DE}。

第三步：删减矩阵。对行扫描，发现所有的行1出现的个数都是大于3的，所以没有必要删除。在对项在频繁2-项集中出现的次数进行计数，都是大于2的。如A在频繁2-项集中出现的次数就是4。所以没有必要删除矩阵。

第四步：生成频繁3-项集为：{ABC},{ABD},{BCD},{BCE},{CDE},利用性质3，发现A在频繁3-项集中出现的次数为2，所以删掉A列。得到矩阵如表5。

第五步：生成频繁4-项集为{BCDE}，整个算法结束。

4 算法的分析

本算法较之文献[7]的算法的不同之处主要在是对频繁k-1-项集的查找的方法上，所以分析主要在查找方法上的分析上。

假设频繁k-1-项集的个数即矩阵的行数为m，频繁k-1-项集的集合的项的个数是p，之前的查找方法需要扫描频繁k-1-项集的次数是p，所以总的扫描行数为pm。使用改进的算法，在计算项在频繁k-1-项集中出现的次数时候，只需要扫描矩阵部分行。如表5中A、B、C项都是需要扫描部分行，所以总的扫描行数是，所以这样一来会较之原来的查找方法节约时间。此外,由表2可知,当事务集的项越多,那么矩阵第一列的字典序不同的项会比较多,由于这种查找方法中根据有序性查找的,则一旦发现扫描的行的第一列的的字典序大于所搜索项的字典序,则停在搜索,那么所扫描的行数与之前的查找方法相比较会大大减少,这种查找方法的优势会更加明显。而整个算法中这种查找会用到k次左右，节约的时间会比较多。用在整个算法上也就降低了时间复杂度。

表5 删减后的矩阵Tab5 The reduced matrix

与apriori算法比较,整个算法由于把事务以矩阵的形式存入内存所以对数据库只是需要扫描一次,而且不需要产生候选项集,节省了内存空间,而且省略了连接和剪枝的时间。

5 结论

本文主要的创新点是对基于矩阵的apriori算法中删减矩阵前的对频繁k-1-项集的查找方法进行了改进，从而降低了算法的时间复杂度，通过分析对矩阵的扫描量从而得出此改进是有效的。但是此算法在数据量比较大的时候对，内存消耗比较大，此问题值得进一步研究。

[1]TANGPang-ning,Steinbach V，Kumar V.Introduction to data mining[M].北京：人民邮电出版社，2006.

[2]BAI Si-xue,DAI Xin-xi.An efficiency apriori algorithm：P_Matrix algorithm[C].ISDPE,2007:101-103.

[3]徐章艳,张师超,区玉明,等.挖掘关联规则中的一种优化的Aprior算法[J].计算机工程,2003(19):83-87.XU Zhang-yan,ZHANG Shi-chao,QU Yu-ming,et al.An optimized apriori algorithm for mining assoeiation rules[J].Compute Engineering,2003(19):83-87.

[4]柴华昕,王勇.Apriori挖掘频繁项目集算法的改进[J].计算机工程与应用，2007,43(24):158-161.CHAI Hua-xin,WANG Yong.Improvement of apriori algorithm[J].Computer Engineering and Applications,2007,43(24):158-161.

[5]崔贯勋,李梁，王柯柯,等.基于改进Apriori算法的入侵检测系统的研究[J].计算机工程与科学，2011(4):40-44.CUI Guan-xun,LI Liang,WANG Ke-ke,et al.Research on an intrusion detection system based on the improved apriori algorithm[J].Computer Engineering and Science,2011(4):40-44.

[6]刘敏娴,马强,宁以风.基于频繁矩阵的Apriori算法改进[J].计算机工程和设计，2012,33(11):4235-4239.LIU Min-xian,MA Qiang,NING Yi-feng.Improved apriori algorithm based on frequent matrix[J].Computer Engineering and Design,2012,33(11):4235-4239.

[7]徐嘉莉.一种基于矩阵压缩的Apriori优化算法[J].微计算机信息，2009,4(3):213-215.XU Jia-li.A high efficiency algorithm based on reducing matrix for apriori[J].Microcomputer Information,2009,4(3):213-215.

[8]苗苗苗,王玉英.基于矩阵压缩的Apriori算法的研究[J].计算机工程与应用，2013,49(1):159-162.MIAO Miao-miao,WANG Yu-ying.Research on improvement of Apriori algorithm based on matrix compression.Computer Engineering and Applications,2013,49（1）：159-162.

[9]傅慧，邹海.基于待与项集的频繁项集挖掘算法的研究[J].计算机工程与设计，2009,30(1):129-131.FU Hui，ZOU Hai.Algorithm of mining frequent itemsets based on pending items [J].Computer Engineering and Design，2009,30(1):129-131.