椭圆曲线密码算法在VPN安全握手中的应用

白永祥

（1．西北大学 信息科学与技术学院，陕西 西安 710127；2．渭南职业技术学院 陕西 渭南 714000）

为防止网络上未授权的用户读取信息，在VPN中，对通过公共网络传递的数据必须实施加密，因此，加密技术是VPN中的一项关键技术。通常VPN采用安全套接层协议（Secure Sockets Layer，SSL）来实现数据的保密性、完整性及认证服务。在SSL会话中，使用证书来验证通信双方的身份，协商加密算法及密钥生成等，通常采用基于RSA的非对称加密算法交换密钥，保证密钥的安全性。由于RSA加密算法进行加密的VPN系统存在不足，我们提出将椭圆曲线加密算法（Elliptic Curve Cryptosystem，ECC）应用于SSL安全握手中。同RSA等常用加密算法相比较，ECC在相同的安全强度下具有密钥长度短，运算量较小，复杂度低等特点，所以在实际应用中可以显著提高运算效率[1]。

1 基于SSL协议的VPN

安全套接层SSL位于TCP和应用层之间，它主要适用于Point-to-Point之间的信息传输，常采用Client/Server结构模式 (简称C/S)，具有保护传输数据以及识别通信机器的功能。SSL主要采用非对称加密体制和X.509数字证书技术,在Internet基础上提供用户和服务器身份的合法性认证、链路上的数据完整性和数据机密性等安全性保证。SSL并不是一个单独的协议，它由两部分组成，上层协议包括SSL握手协议、SSL密码算法选择协议和SSL警报协议，下层协议为SSL记录协议。SSL握手协议（SSL Handshake Protocol）主要维护客户和服务器之间的会话状态，为通信双方建立安全的传输信道，它建立在SSL记录协议之上，是SSL协议中最复杂的部分。在执行握手协议的过程中实现对服务器的身份认证，或者对通信实体双方身份进行鉴别，协商确定加密和鉴别算法以及协商密钥。加密算法可以选择DES、3-DES、IDEA、RC4等，鉴别算法可使用MD5、SHA-1、SHA-2等，密钥交换常采用RSA公钥算法来完成，当然还有其他一些辅助算法，如压缩算法等。当这些顺利完成后，才可以实现服务器和客户机之间逻辑意义上的“安全握手”，再下来应用程序才能开始交换数据，具体过程如图1所示。

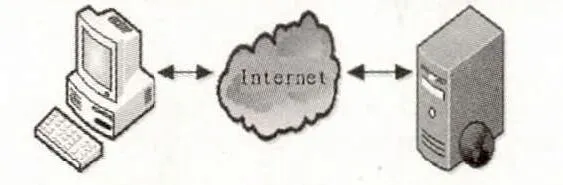
图1 客户/服务器结构模式Fig.1 Client/Server structure mode

目前，SSL VPN接入技术有3种：Web代理、端口转发和隧道技术。作为一种远程接入技术，SSL VPN必须解决终端安全问题，并且真正的提供全网接入能力，客户端（Client）将数据SSL封装后发送到服务器，服务器端(Server)将来自客户端的数据进行正确解码后转发到SSL协议的应用层，要求使用非对称加密算法协商密钥，传统的基于RSA加密算法的SSL服务器CPU大量时间耗费在处理SSL加解密上，只有少量时间处理应用程序逻辑。本文基于椭圆曲线密码体制的优势将ECC加密算法应用到握手协议的加解密过程中。SSL握手协议有多种操作模式，图2包括了所有工作模式下所涉及的消息[2]。

表1 SSL协议结构Tab.1 The SSL protocol srtucture

2 椭圆曲线密码体制

图2 SSL握手协议Fig.2 SSL handshake protocol

2.1 椭圆曲线加密体制原理

1985年，Miller和Koblitz各自独立的提出了椭圆曲线公钥密码[3]，它是基于有限域上的椭圆曲线构成加密体制，其安全性基于有限域上椭圆曲线离散对数问题 （Elliptic Curve Discrete Logarithm Problem,ECDLP）的难解性。ECDLP难解性是指：对于曲线上给定的离散点P和Q，难以找到整数I，使得I×P=Q。设P为公钥，Q为私钥，其安全性就表现为知道P无法推导Q。对于有限群上的x和y，若存在正整数n，使得y=xn，求解n=logxy的问题称为有限群上离散对数问题（Discrete Logarithm Problem,DLP）。而对椭圆曲线上离散点P和Q，求解I，使得I×P=Q称为椭圆曲线离散对数问题，ECDLP的难解性优于DLP。

由于椭圆曲线加密算法具有密钥长度短，占用存贮空间少、灵活性好等特点，所以在运算速度和存贮空间方面有很大的优势，与同长度密钥算法相比较安全性高，是一种能适现代通信技术及信息安全技术发展的先进加密体制。由于服务器端的CPU处理能力和存储空间都有限，所以椭圆曲线加密算法相对于以往基于RSA加密算法的握手过程具有绝对的优势，目前已成为非对称密钥加密体制中的研究热点。

2.2 ECC加密和解密算法原理

非对称加密方案可用来提供机密性，但加密过程比较复杂，运算量大，不适应于对大量数据的加密解密，一般应用在少量数据的加密上，如信用卡号码、密钥加解密。大批量的数据文件加解密使用运算速度更快的对称密钥算法来完成。下面给出了加密和解密方案[1]：

加密过程，当用户Alice发送信息M给用户Bob时，用户Alice执行下列步骤：

1)找出 Bob的公钥 QB；

2)将信息M表示成椭圆曲线E(Fq)上的一点m，且m∈Fq；

3)在区间[1,n-1]内随机选取一个整数k；

4)计算点(x1，y1)=kP；

5)计算点(x2，y2)=kQB，如是 x2=0，则返回到第 3)步；

6)计算 c=m×x2；

7)将加密数据(x1，y1，c）传送给 Bob。

解密过程，当Bob解密从Alice收到的密文 (x1,y1,c)时，Bob执行下列步骤：

1)Bob 使用私钥 dB，计算点(x2,y2)=dB(x1,y1)，得出 x2∈Fq；

在上述过程中，QB=dP是公开的，如果除Alice、Bob外的第三者能解答椭圆曲线上的离散对数问题，就能从dP中求出d，从而解密信息m。

3 ECC优势及其在SSL安全均衡中的应用

1)ECC优势:在相同安全性下，椭圆曲线加密算法的密钥短，所以计算量小、占用存储空间小、处理速度快，与RSA相比椭圆曲线的密钥长度和系统参数要小得多，比如：160位ECC与1 024位RSA具有相同的安全强度，210位ECC安全强度等同于2 048位RSA，很明显ECC它所占用存储空间要小得多，相应的椭圆曲线加密算法的带宽要也非常低。此外，由于椭圆曲线具有丰富的群结构和多选择性，可以通过改变参数设置获得不同的曲线，所以，椭圆曲线加密算法的灵活性要高于RSA加密算法。

2)对ECC加密算法的优化:椭圆曲线有理点加法运算构成一个群，设P是椭圆曲线上的一个点，将P自身相加k倍在运算，称为倍点运算。在椭圆曲线公钥生成和加密解密算法中需要大量的倍点运算，因此，对倍点运算的优化意义重大，倍点运算如下：

计算倍点最常用的方法是二进制法，具体步骤如下：

①令Q=P；

②For i=l-1 to 1 step-1

Q=2Q

if ni=1 then Q=Q+P

③输出Q。

具体的倍点运算优化算法如下[4]：

①将k表示成二进制数形式，k=(knkn-1…k1k0)2；

②去掉 k=(knkn-1…k1k0)2的最高位 kn，得(ki-1…k1k0)2；

③P1=P,P2=2P,i=1；

若 i≤2h-1，则作 P2i+1=P2i-1+P2；

④Q=O；

⑤若i≥0转⑥，否则转⑧；

⑥若ki=0，则Q=2Q，i=i-1否则转⑦；

⑦Q=2i-l-1Q+P(ki…kl),i=l-1 转⑤；

⑧输出Q。

采用常规方法，需进行n次点加运算；在以上算法中，平均只须3/2[log2n]次运算，最多需要2[log2n]次运算。

在对明文m加密之前，首先要将明文m映射到椭圆曲线有限域Fq上的一个点，这就需要判别数是否为模P下的平方剩余。现有的平方剩余判定算法只简单地根据平方剩余定义来判别，如果涉及大数的平方运算和取模运算，算法效率就会非常低，所以如何提高平方剩余判定方法的效率非常关键。

如果明文m映射到点Pm(x,y)上，即满足：256≤x≤256(m+1)，Pm(x,y)∈Fq。 这个问题可以转换为：

给定一个x，判定A=x3+ax+b是否是模p下的平方剩余。即判定A/p是否为1，即如下情况所示。

4 基于ECC的SSL安全均衡握手协议

Alice向Bob在传输数据前，就必须知道Bob的公钥，如何保证Bob的公钥不被人假冒或修改，这里就需要对Bob进行身份认证，通常使用数据证书实现这一目标。所谓数据证书就是网络通信中的“身份证”，一般由一个权威机构认证机构颁发（CA），客户证书就是一份关于用户公钥的文件，采用数据签名技术来保证文件的真实性。在设计适合于VPN系统的安全协议时，首先要解决这个问题[5]。这里选用一种简化了的X.509标准的证书形式，用户Bob的证书可能如下：

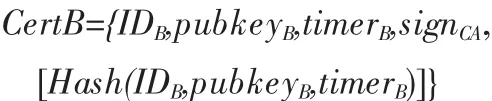
在基于ECC密码算法体制下，首先要为Alice、Bob生成公钥和私钥，然后才能进行加密、解密和签名，整个这个过程非常复杂，此处不再详述，有兴趣的读者可以阅读相关资料。这里简单描述一下形成过程。

1)认证中心选择定义在有限域上的椭圆曲线E[GF(q)]

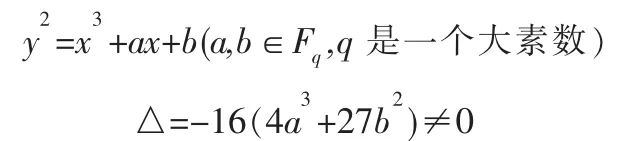
E上的点构成循环群P∈E[GF(q)]，CA选取一条椭圆曲线，G称为基点，且=k，k≥160位，这样选择的椭圆曲线能保证其上的离散对数难解性[5]。

2)CA随机选择一个数KCA∈{1,2,…,l-1}，作为其私钥，(KCA,l-1)=1，计算公钥PUCA，并公开公钥，以便对服务器端和客户端的证书进行签名。

3)客户随机选择一个数Cd∈{1,2,…,l-1}，作为其私钥，(Cd,1）=1，计算PUC作为其公钥，并提交给CA为其颁发证书：

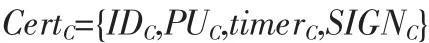
这里SIGNC是CA的签名。用户联网时，为其生成私钥和公钥，同时根据用户提交的有效信息生成证书：

4)客户接收到服务器端证书后，首先要验证证书的合法性，并利用证书中的信息IDC,PUC,TimerC生成：

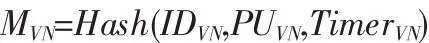
然后验证：

如果不成立，立即停止继续执行，否则，则签名有效，证书合法，并计算kP,k,PUVN和Q=(SVN+k)PUVN=(X,Y)

X和Y分别是点Q的坐标。保存{k,kP,kpVN}和X。这里一定要注意k在每次进行身份认证的时候都必须重新随机产生。

5 结论

在椭圆曲线加密算法中采用160 bits的密钥可与1024bits密钥的RSA算法的安全性相当，且随着模数的增大，它们之间安全性的差距猛烈增大[6]。本文首次把椭圆曲线加密算法技术运用到了SSL VPN的安全握手技术中，并使用了倍点加速优化技术，与传统的加密和解密过程相比较，使SSL服务器的工作效率得到大大提高。

[1]王学理，裴定一.椭圆与超椭圆曲线公钥密码的理论与实现[M].北京：科学出版社，2006.

[2]Cryptography and network security principles and practice,fifth edition[M].北京：电子工业出版社.2011.

[3]祝跃飞，张亚娟.椭圆曲线公钥密码导引[M].北京：科学出版社，2006.

[4]Jose H.Silverman.The arithmetic of elliptic curves[M].Springer-Verlag.1992.

[5]李丽，刘福军.基于ECC加密算法的SSL VPN安全握手技术研究[J].辽宁工业大学学报,2008(8):228-231.LI li,LIU Fu-jun.The research of SSL VPN security handshake technology based on ECC[J].Journal of LiaoNing University of Technology,2008(8):228-231.

[6]吴世忠，祝世雄等.应用密码学协议、算法与C源程序[M].北京：机械工业出版社,2010.