基于LS-SVM的压缩机防喘振非线性模型预测控制

金 星，王照明，姜长泓

（长春工业大学 电气与电子工程学院，长春 130000）

本文设计了一个关于压缩机防喘振非线性模型预测控制系统，该控制系统可以有效地在减小喘振线和控制线之间距离的同时避免喘振的发生。根据预测模型的预测作用，提前判断工作点是否越过控制线，减小了执行器调节时间对防喘振控制动作的影响，有效缩短了控制线和喘振线之间的距离[2]；将防喘振条件分别加入到期望轨迹和滚动优化算法的限制条件中，达到防喘振的目的。

1 压缩机防喘振非线性模型预测控制系统的设计

出口压力和质量流量是压缩机的2个主要变量，决定了压缩机工作点的位置。在工业生产中，控制好这2个变量是至关重要的。压缩机是一个非线性的系统，在设计中，包含2个非线性预测模型，一个是出口压力预测模型，另一个是质量流量预测模型。通过转速控制出口压力，执行器为驱动器；通过出口节流控制质量流量，执行器为出口节流阀。整个控制系统主要分为出口压力预测控制和质量流量预测控制，每一部分分别包含模型预测、参考轨迹、滚动优化和反馈校正[3]，如图1所示。

1.1 预测模型

预测控制是一种基于模型的控制算法，预测模型的功能是根据对象的历史信息和未来输入预测其未来输出，本文采用LS-SVM建立预测模型，LSSVM既能够降低模型处理的复杂程度，又能保证模型参数的准确[4]。压缩机的出口压力模型可表示为

式中：kt和v为系统输入，分别是压缩机回流阀的控制信号和压缩机转速；p为系统输出，是压缩机的出口压力；n为模型阶次；m为控制输入阶次，m≤n。

l个采样点的采样集可表示为

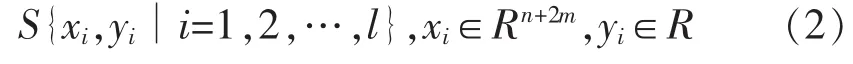
式中：xi=［p（i），…，p（i-n），v（i），…v（i-m），kt（i），…，kt（i-m）］；yi=p（i+1）。模型的处理是寻求一种最佳的函数f为

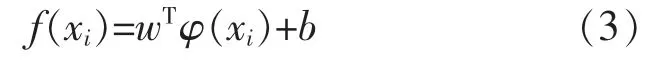
式中：φ（·）为映射函数；w为系数；b为偏置量。基于LS-SVM理论，压缩机出口压力模型可以实现，通过解决如下二次项问题：

与亲密关系丧失不同的是，死亡凸显还会额外导致高自尊者职业情感的降低，这一效应可能是由死亡凸显所引发的无意义感所导致，而亲密关系丧失不具备这一心理效应。 人是活在意义之网上的动物，我们需要相信自己生活在一个有意义的世界中，但死亡却否定一切意义，凸显了我们作为自然界中一个普通生物体的存在，给个体带来了恐惧、虚无等消极的情绪体验，也许正是这些消极情绪的蔓延削弱了高自尊者的职业情感。

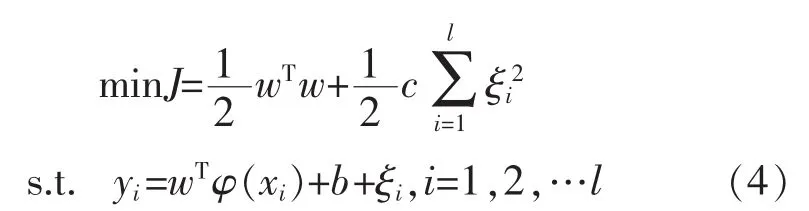
式中：c为惩罚系数；ξi为误差。

式（4）的拉格朗日构建为

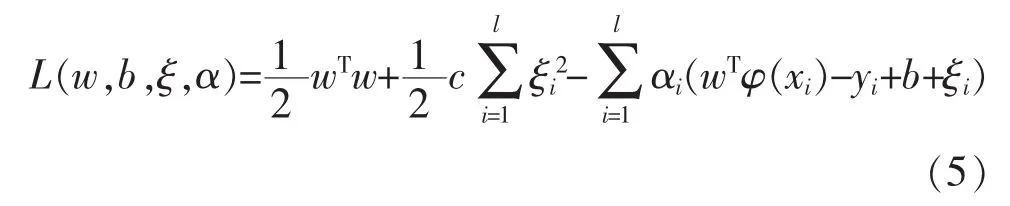
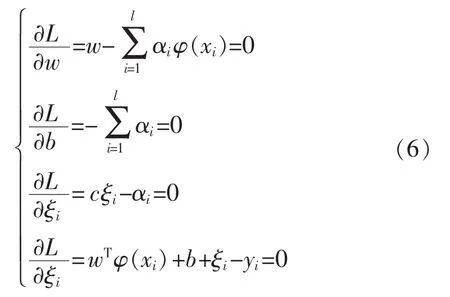
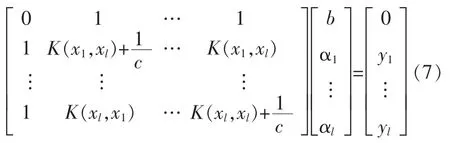
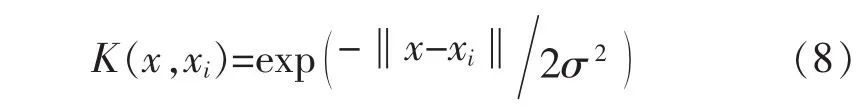
对式（7）解线性方程组，可得出口压力预测函数为

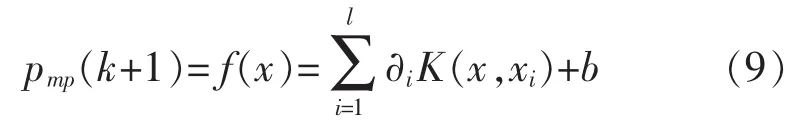
同理，质量流量的预测模型函数可由上述方式得到。

1.2 参考轨迹

对于压缩机，它的出口压力参考轨迹可表示为

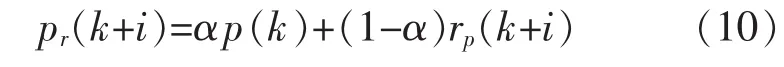
式中：pr（k+i）为出口压力的参考轨迹；α（0，1）为模糊系数；rp（k+i）为出口压力的期望轨迹。采用指数变化的形式来消除误差，并且要求压缩机的工作点绝对不能越过控制线，因此rp（k+i）被定义为

式中：sp（k）为排除压力的设置点；εp（k）为误差；Ts为采样时间；Tref为参考时间，它可以决定反应速度，rm（k+i）为质量流量的期望轨迹，pCL（rm（k+i））为 rm（k+i）在控制线上对应的排除压力。通过在参考轨迹中加入限制条件，可以确保由参考轨迹所确定的工作点始终位于控制线的右侧。

1.3 滚动优化

滚动优化实际上就是用最小的控制器输出能量获得最优的控制效果[5]。以压缩机出口压力为例，K时刻，压缩机出口压力的性能指标为

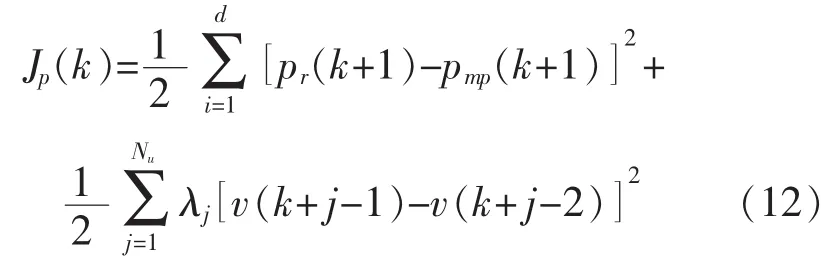
式中：λj为控制量的加权系数；d为预测时域；Nu为控制时域，一般d≥Nu≥1。考虑到离心压缩机转速、工作范围以及控制线的限制，防喘振控制问题可转化为如下的优化问题：

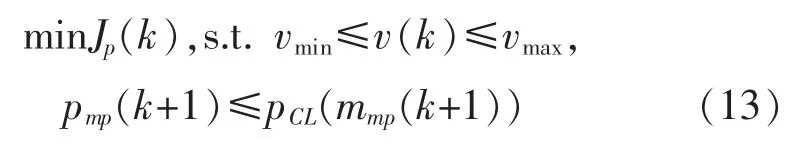
式中：vmin和vmax分别为压缩机的最小和最大转速；mmp（k+1）为质量流量预测模型的输出；pCL（mmp（k+1））为mmp（k+1）在控制线上对应的排除压力。 压缩机出口压力的控制输入通过控制质量流量的输入，使得控制器始终将工作点控制在控制线的右侧[6]。

1.4 反馈校正

模型预测输出与真实输出之间必然存在误差，为保证精度，需要对误差进行反馈校正，以压缩机出口压力为例，加入反馈后的预测值校正公式为

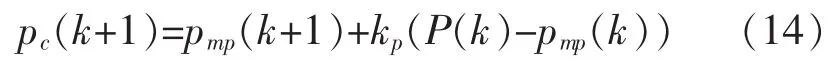
式中：kp为误差修正系数；P（k）为压缩机出口压力；pmp（k）为压缩机出口压力预测模型的输出。

2 仿真和实验

2.1 非线性预测模型的仿真识别

对压缩机出口压力和质量流量的非线性预测模型在脱机下进行。压缩机出口压力与质量流量预测模型的回归向量分别为[7]

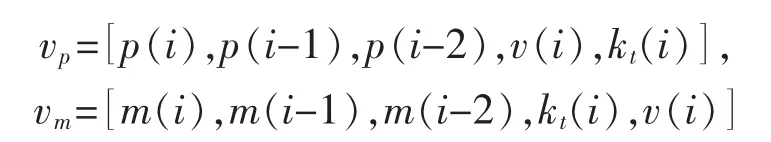
通过记录压缩机的工作数据，从中选取500个测试样本。归一化处理后，获得300个样本点作为训练集，最后取得200个样本点作为测试集。用k-折交叉算法， 得 εp=1.55，σp2=0.49，εm=3.4，σm2=0.28。训练集用来评价LS-SVM预测模型，测试集用于辨识模型。辨识误差的数据如图2所示，出口压力LSSVR模型的最大辨识误差为0.07 MPa，质量流量LS-SVR模型的最大辨识误差为0.06 kg/s，可以认为它们符合压缩机的动态特性。

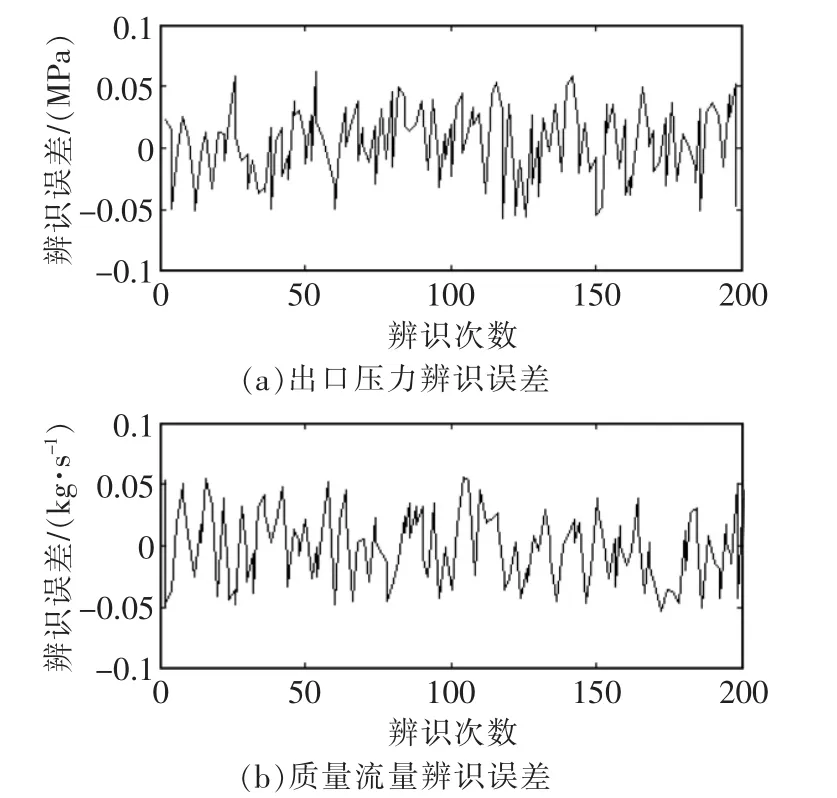
图2 压缩机LS-SVM模型校验误差Fig.2 Predict model verify error

2.2 工作点变化实验

应用预测模型，对压缩机工作点的变化进行研究，首先采用可变极限流量法进行仿真，在t=5 s时改变压缩机的工作点由图3中C点至D点，图3下半部分是质量流量和出口压力的响应曲线。由图中可见，新工作点D距喘振线较近，当工作点变化至D点附近时[8]，由于控制器超调等因素的影响，致使工作点继续向左侧移动，从而越过了控制线。由于可变极限流量法无法提前判断工作点的运行轨迹，因此只有当工作点越过控制线时，控制器才会发出控制作用打开回流阀，但由于回流阀打开的延迟特性，导致工作点没有及时回到控制线右侧，而是继续向左侧移动，越过了喘振线，因此导致了压缩机在大约t=7.5 s时发生了喘振。

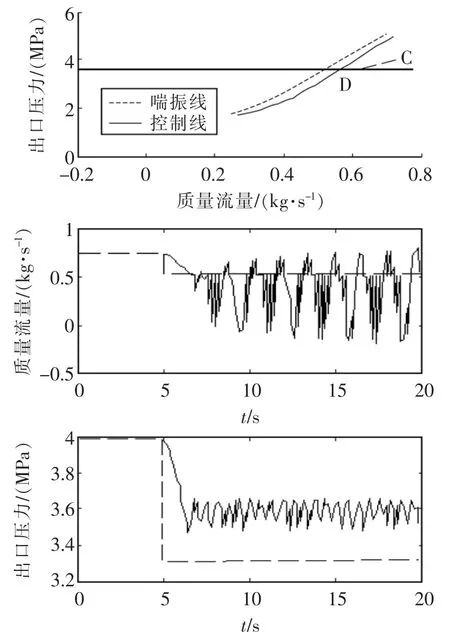
图3 可变极限流量法防喘振仿真Fig.3 Avoidance control effect

采用本文提出的防喘振预测控制策略进行仿真，在t=5 s时改变压缩机的工作点由图4中C点至D点，图4下半部分是质量流量和出口压力的响应曲线。由图中可见，基于预测控制的高级控制方式，控制器可以提前判断工作点是否越过控制线，因此可以提前发出控制动作打开回流阀，避免了喘振发生，并且超调量小，工作点变化平稳，使压缩机稳定工作于D点[9-10]。

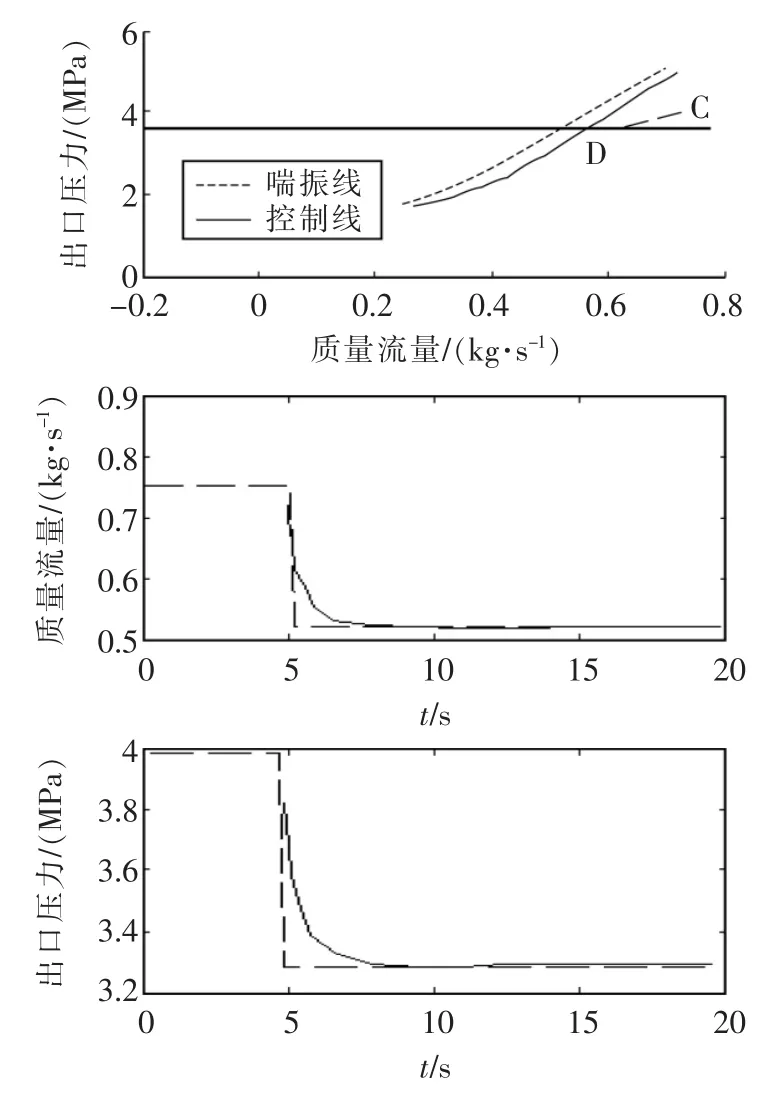
图4 防喘振预测控制仿真Fig.4 Predictive control effect

3 结语

为了提高压缩机的运行效率，设计了压缩机防喘振非线性模型预测控制系统，这个系统可以在减小喘振线和控制线之间距离的同时有效避免喘振的发生。压缩机的动态模型通过LS-SVM进行建造。根据预测模型的预测作用，提前判断工作点是否越过控制线，减小了执行器调节时间对防喘振控制动作的影响，有效缩短了控制线和喘振线之间的距离；将防喘振条件分别加入到期望轨迹和滚动优化算法的限制条件中，达到防喘振的目的。仿真结果表明，基于LS-SVM的压缩机防喘振非线性模型预测控制策略可以达到理想的效果。

[1]鲁国强.一种离心压缩机防喘振控制策略及其应用[J].化工设备与管道，2010，47（5）：43-46.

[2]王传鑫.离心压缩机综合控制方法研究[J].大连理工大学，2010，25（5）：51-56.

[3]陈静，石晓瑛，许智榜，等.自适应预测控制在纸浆浓度控制系统中的应用[J].自动化技术与应用，2003，22（8）：49-51.

[4]时维国，宋存利.基于脉冲响应的预测控制算法及仿真[J].大连铁道学院学报，2004，26（4）：51-54.

[5]张彩虹，滕军.基于二次型性能指标的控制器优化布置方法[J].地震工程与工程振动，2003，23（3）：184-189.

[6]杨帆，赵红强.DCS在压缩机防喘振控制系统中的应用[J].石油化工自动化，2003（4）：49-51.

[7]何海琴，王龙一，侯森.线性压缩机RC负载全阻抗输出特性研究[J].低温工程，2013（2）：13-19.

[8]王志国.防喘振控制方案在废酸再生装置压缩机中的应用[J].广东化工，2010，37（6）：268-269.

[9]陈广，郭建岭，方留安.四合一机组防喘振控制探讨[J].石油化工自动化，2012，48（6）：43-46.

[10]姜林，石敬君.浅析离心式压缩机喘振原因及解决措施[J].农家科技，2013（10）：159-161.