偏心度与间隙比对轴流泵流动激励力的影响

王珏星　杨爱玲　陈二云　戴韧　李国平

摘 要： 叶轮偏心将会引起轴流泵叶轮顶部间隙沿周向不均匀，从而导致附加的流动激励和噪声.利用计算流体力学商业软件Fluent模拟不同偏心度和间隙比的轴流泵非定常流场，研究周向非均匀间隙对泵内压强脉动及叶轮激励力的影响.结果表明：壁面压强脉动强度并不是在最小间隙处达到最大，而是出现在偏离最小间隙处约30°～60°的方向，并随着间隙比增大，脉动强度最大值发生位置逐渐向最小间隙处靠拢；同时，偏心造成的非均匀叶顶间隙引起了轴频处的压强脉动，在间隙比为2.5%下偏心度从0%增加到60%，轴频处的压强脉动相对增量为661.54%；叶轮受到的径向激励力时均值与偏心度呈线性关系，其斜率与间隙比的平方根成正比.

关键词：非均匀叶顶间隙； 偏心度； 间隙比； 压强脉动； 叶轮激励力

中图分类号： TH 312 文献标志码： A

随着流体机械以及涡轮机械载荷的不断加大，轴系涡动现象日益显著.轴系涡动导致叶轮顶部间隙沿周向呈非均匀分布，产生附加流动激振力，从而引起旋转机械振动并辐射噪声.这一问题已得到国内外学者的关注.

早在上世纪五、六十年代，Thomas[1]、Alford[2]对汽轮机及燃气轮机的转子偏心进行了研究，结果发现叶轮高速旋转时会出现偏心现象，并且Alford导出了叶轮偏心引起的激振力公式，该力也被称为Alford力.1984年Vance等[3]利用鼓风机进行的偏心实验证实了Alford力的存在.1994年晏砺堂等[4-5]对偏心引起的自激力作了理论和实验分析，研究表明自激力会推动转子反进动.2006年唐云冰等[6]以Jeffcott转子为例研究了叶轮偏心间隙引起的气流激振力对转子稳定性的影响规律.2008年黄来等[7]通过数值模拟方法分别对不同间隙、偏心度、转速对气流激振力的影响进行了研究.2011年游磊等[8]对轴流泵振动加速度作了监测，证实转速为960 r·min-1时存在轴偏心和叶轮偏心.

国内外公开发表的研究资料[9]表明，叶轮在旋转时会出现偏心现象，且这种叶轮偏心引起的周向叶顶间隙不均匀性会随着叶片载荷的增加而增加.学者们对汽轮机的转子偏心间隙问题高度关注，并开展了深入细致的研究.然而，关于因转子偏心导致的周向非均匀叶顶间隙对轴流泵性能与流动激励力的影响的研究十分匮乏.本文利用数值方法模拟在不同偏心度、间隙比下叶顶非均匀间隙对轴流泵壳壁静压脉动以及激励力的影响，以期对今后研究水泵振动以及噪声问题有所帮助.

1 几何模型及数值求解方法

1.1 轴流泵几何参数

本文研究的轴流泵叶轮轮毂半径R1=66.67 mm、叶轮叶顶半径R2=125 mm、叶片数Z=4、额定转速n=960 r·min-1、额定流量Qs=300 m3·h-1.图1为轴流泵叶轮几何参数示意图，其中：δ0为初始均匀叶顶间隙；e为叶轮偏心量；h为叶高.叶轮在工作过程中，由于转轴涡动及流体不平衡力作用，叶轮可能偏离中心位置，形成周向不均匀的叶顶间隙.在实际情况下，e在叶轮工作过程中一直随时间变化，直接采用数值方法模拟叶轮偏心运动过程带来的非均匀叶顶间隙时，需不断计算叶轮位置并生成新的旋转叶轮及间隙区域网格，需模拟的时间物理尺度包括偏心运动周期和叶轮旋转周期，这些都存在较大的困难.本文对模型进行了简化，忽略叶轮偏心运动的动力特性，在不同偏心度下模拟轴流泵流场，对比分析非均匀叶顶间隙对轴流泵水力性能、流动非定常激励力的影响.表1给出了本文模拟叶轮偏心的模型参数，其中：J为间隙比，为δ0与h的比值；P=e/δ0，为偏心度，用于衡量非均匀叶顶间隙的程度，P=0%对应于叶轮位于泵管中心的状态.

1.2 计算域及计算网格

图2为轴流泵模型的计算域示意图，其中：r为径向轴；z为轴向轴；ω为叶轮旋转角速度；D2为管径.为了简化几何模型，忽略了轴面几何细节，并在叶轮前、后分别加了一段长为6倍管径的延长段.计算域由叶轮域、间隙域、进口延长域和出口延长域4部分组成，其中叶轮域为旋转域，其它域为静止域.

计算域采用结构网格进行离散，总体网格数约162万，其中：叶轮域网格数为101万；间隙

域网格数为18万；进、出口延长域网格数均为22万左右.图3～4分别为叶轮域和间隙域网格轴向视图及其中的局部放大图，图3中A为叶轮域和间隙域交接处；B为叶轮叶根前缘处.

1.3 数值计算方法及边界条件设置

轴流泵的工质为水，在常温常压下一般视为不可压液体.因此，本文采用三维不可压的雷诺时均N-S方程组作为定常流场的控制方程，相应的湍流模型为k-ε RNG模型，流场迭代求解采用SIMPLEC压力速度耦合方法.将获得的定常流场收敛解作为初场，采用大涡模拟方法计算轴流泵内的非定常场，从而获取泵内压强脉动与激励力信息.在非定常计算中，时间步长ΔT=T/360，T为叶轮旋转周期.每迭代一个时间步长，相当于叶轮旋转了1°.采用该时间步长，流场脉动信号中最高分辨频率f不小于2 880 Hz（f=1/（2ΔT）），远高于叶片通过频率64 Hz.

轴流泵的流场边界条件主要有3类：进口边界、出口边界及固壁边界.进口边界以质量流量的进口方式给定，该方式在已知进口流量的情况下相比速度入口更为方便，因为不需要考虑进口截面上的速度分布.在出口压强未知的情况下采用自由出流条件，出口边界条件为默认流体出口处流动已充分发展，法向速度梯度为零.计算中，无论是静止固壁（壳壁）还是运动固壁（叶片表面、轴面），均采用无滑移边界条件，即相对固体壁面流体的法向与切向速度等于零.对计算域动静交界面的处理，本文在定常计算中采用多重坐标系，而在非定常计算中采用滑移网格.

1.4 网格无关性验证

为了确定网格的总体尺度，本文分别选取94万、123万、162万、205万等4种网格数，在相同的转速、湍流模型以及边界条件下对轴流泵性能进行计算.

图5给出了间隙比为2.5%、叶轮处于泵体中心（即P=0%）时网格数对水泵扬程H和效率η的影响.图中横坐标为无量纲流量，例如Q/Qs=1.0表示额定流量.需要说明的是，这4种网格数仅考虑了叶轮域网格的疏密变化，其它计算域的网格数保持不变.从图5可知，随着网格数增加，水泵扬程和效率均逐渐增加，但增加趋势逐渐放缓.在额定流量下，网格数从94万增加到205万，η增加了3%；从162万增加到205万，η仅增加了0.26%，增加幅度明显减小.可见，选择162万和205万网格数均可满足计算要求，但采用这4种网格数在相同的并行计算机上获得收敛数值解的计算时间分别为4、6、7、11 h左右.如果进行非定常计算，获得稳定的非定常流场解所需时间是相应定常计算时间的20多倍.综合数值解准确度和计算效率两方面因素，本文后续的轴流泵模型在相同的网格划分方式下，网格数均控制在162万左右.

2 计算结果及分析

2.1 不均匀叶顶间隙对轴流泵水力性能的影响

图6（a）、（b）分别给出了间隙比为2.5%不同偏心度的扬程和效率.随着叶顶间隙的不均匀程度增加，小流量情况下扬程和效率几乎未受影响，而在大流量情况下扬程和效率均受到一定影响，并且随着叶顶间隙的不均匀程度增加，扬程和效率均有所增加.以额定工况下Q/Qs=1.0为例，从偏心度0%增加至60%，H增加了5.43%，η增加了1.58%.

2.2 不均匀叶顶间隙对壳壁压强脉动特性影响

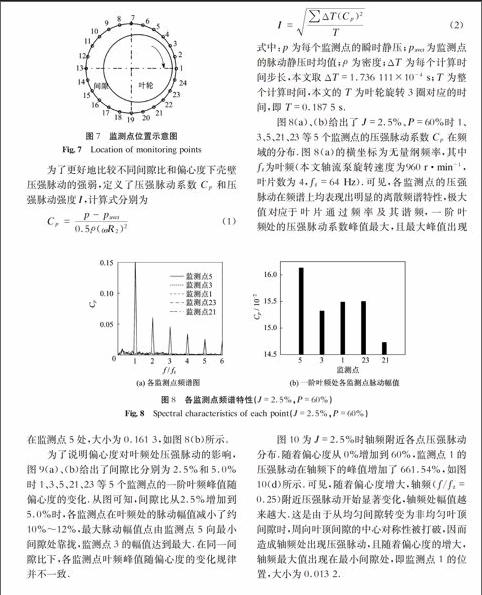
为了分析不均匀叶定间隙对轴流泵内非定常流场的影响，在不同的间隙比和偏心度下计算了轴流泵非定常流场，计算工况为轴流泵额定工况.图7给出了轴流泵壳体壁面上24个监测点的分布，相邻监测点间的周向夹角均为15°.

式中：p为每个监测点的瞬时静压；paver为监测点的脉动静压时均值；ρ为密度；ΔT为每个计算时间步长，本文取ΔT=1.736 111×10-4 s；T为整个计算时间，本文的T为叶轮旋转3圈对应的时间，即T=0.187 5 s.

图8（a）、（b）给出了J=2.5%、P=60%时1、3、5、21、23等5个监测点的压强脉动系数Cp在频域的分布.图8（a）的横坐标为无量纲频率，其中fz为叶频（本文轴流泵旋转速度为960 r·min-1，叶片数为4，fz=64 Hz）.可见，各监测点的压强脉动在频谱上均表现出明显的离散频谱特性，极大值对应于叶片通过频率及其谐频，一阶叶频处的压强脉动系数峰值最大，且最大峰值出现在监测点5处，大小为0.161 3，如图8（b）所示.

为了说明偏心度对叶频处压强脉动的影响，图9（a）、（b）给出了间隙比分别为2.5%和5.0%时1、3、5、21、23等5个监测点的一阶叶频峰值随偏心度的变化.从图可知，间隙比从2.5%增加到5.0%时，各监测点在叶频处的脉动幅值减小了约10%～12%，最大脉动幅值点由监测点5向最小间隙处靠拢，监测点3的幅值达到最大.在同一间隙比下，各监测点叶频峰值随偏心度的变化规律并不一致.

图10为J=2.5%时轴频附近各点压强脉动分布.随着偏心度从0%增加到60%，监测点1的压强脉动在轴频下的峰值增加了661.54%，如图10（d）所示.可见，随着偏心度增大，轴频（f/fz=0.25）附近压强脉动开始显著变化，轴频处幅值越来越大.这是由于从均匀间隙转变为非均匀叶顶间隙时，周向叶顶间隙的中心对称性被打破，因而造成轴频处出现压强脉动，且随着偏心度的增大，轴频最大值出现在最小间隙处，即监测点1的位置，大小为0.013 2.

图11给出了间隙比分别为2.5%和5.0%时，不同偏心度下轴流泵壳体内壁面监测点的压强脉动强度的分布.从图可看出，无论J=2.5%还是J=5.0%，最小间隙处（监测点1）的脉动强度均大于最大间隙区（监测点13），且壳壁上半圈（监测点1至13点）的脉动强度普遍大于壳壁下半圈（监测点13至24），这是由于叶轮旋转造成的非均匀间隙流道非对称效应.由于叶轮旋转，在间隙区上部流道逐渐减小，为膨胀过程，而下半圈正好为压缩过程.同样的原因，壳壁脉动强度最大处并不出现在最小间隙处，而是在上半圈偏离最小间隙处约30°～60°处（监测点3至5点）.图11还表明，随着间隙比从2.5%增加到5.0%，各偏心度下的最大脉动强度减小.这表明随叶顶间隙增加，间隙内流动由于偏心引起的膨胀和压缩效应减弱，此时，最大脉动强度位置也向最小间隙处偏移.

2.3 叶轮激励力分析

由于在未偏心时，叶轮流动参数呈周向对称，因而径向力约为零.随着偏心度增加，存在径向不平衡，使得径向力变大.图12给出了不同间隙比时径向激励力时均值随偏心度的变化.从图可知看，当J=2.5%，偏心度分别为0%、20%、40%、60%时，叶轮受到的时均径向激励力Fr分别为0.295、5.398、10.518、17.225 N；当J=5.0%，Fr分别为0.273、7.775、16.455、24.365 N.若以线性规律拟合数据，当J=2.5%，直线斜率为0.282；当J=5.0%，斜率为0.402，其斜率变化规律与间隙比的平方根成正比.

对间隙比J=2.5%的轴流泵模型的径向力Fr时域信号进行傅里叶变换，不同相对偏心比下径向激励力频谱图如图13所示.从图可看出，随着偏心度P不断增加，径向力的轴频信号（f/fz=0.25）幅值也不断增加，且随着偏心度的增加，径向力Fr主要频谱峰值出现在f/fz=1.6，即约102 Hz处.

3 结 论

本文利用Fluent软件对不同偏心度和间隙比的轴流泵模型进行了模拟计算，研究结果表明：

（1） 从壳壁的压强脉动强度分布规律看，无论间隙比为多少，最小间隙区的压强脉动强度均大于最大间隙区.但最小间隙处（监测点1）并不是压强脉动强度最大处，而是在距最小间隙约30°～60°左右（监测点3至监测点5段内）的非均匀叶顶间隙膨胀区.随着间隙比增大，最大压强脉动强度向最小间隙处偏移.

（2） 因未考虑叶轮质心运动，故从频谱上看，壳壁的脉动表现出明显的离散频谱特性，且极大值对应于叶片通过频率和其谐频.但叶轮在旋转偏心时所带来的非均匀叶顶间隙会对泵内流场在轴频处压强脉动产生影响.随着叶顶间隙的非均匀程度增大，即随偏心度增大，轴频下压强脉动增加，且增幅远大于叶频处的脉动增幅.

（3） 叶轮径向激励力的时均值与偏心度成正比，其斜率则与间隙比的平方根成正比，且随着偏心度的不断增加，径向力的轴频信号幅值也不断增加.

参考文献：

[1] THOMAS H J.Unstable natural vibration of turbine rotors induced by the clearance flow in glands and blading[J].Bull.de lAIM，1958，71（11/12）：1039-1063.

[2] ALFORD J S.Protecting turbomachinery from selfexcited rotor whirl[J].Journal of Engineering for Gas Turbines and Power，1965，87（4）：333-343.

[3] VANCE J M，LAUDADIO F J.Experimental measurement of Alfords force in axial flow turbomachinery[J].Journal of Engineering for Gas Turbines and Power，1984，106（3）：585-590.

[4] 晏砺堂，洪杰，李其汉，等.压气机叶轮偏心引起的自激力和稳定性的理论分析[J].航空动力学报，1994，9（2）：157-160.

[5] 晏砺堂，洪杰，李其汉，等.压气机叶轮偏心引起的自激力和稳定性的实验研究[J].航空动力学报，1994，9（2）：161-164.

[6] 唐云冰，高德平，罗贵火，等.叶轮偏心引起的气流激振力对转子稳定性影响的分析[J].航空学报，2006，27（2）：245-249.

[7] 黄来，骆名文，丁学俊，等.叶轮偏心间隙气流激振力的数值模拟[J].流体机械，2008，36（4）：19-21.

[8] 游磊，方方，李平勇，等.轴流泵振动加速状态监测诊断系统的研究与设计[J].四川大学学报，2011，43（S1）：236-239.