自动锚泊定位系统的张力混合优化算法

苏晓宇， 金鸿章， 胡晓东

(1.上海工程技术大学电子电气工程学院，上海201620;2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001;3.中船重工第七0四研究所，上海200031)

0 引言

为了改善传统锚泊定位系统定位精确度低的缺点，本文从经济性及安全性角度出发，提出一种新的基于锚链切换控制的自动锚泊定位方案。该方案为半潜平台提供均匀分布的水平回复力以平衡环境扰动，以保持其在海面上的位置及安全性。据以往的海洋平台事故资料，当锚泊事故发生时，首先均是受力最大的锚链断裂，环境外力在余下的缆绳中重新分配又引起余下锚链中受力最大的断裂直至全部断裂，导致严重的后果［1］。因此，环境力在锚链上的分配不均是安全的大隐患，有时即使环境载荷不大，但由于受力严重不均还是有可能产生事故。所以，研究一种使锚链受力均衡的方法尤为必要。所提出的自动锚泊定位方案是以张力的均匀分布为基础，优化方法的效率和精确度将直接影响整个系统的运行速度和定位精确度，传统的优化方法则存在各自的局限性，因此利用全局搜索和局部搜索相结合的混合优化策略来提高优化效率，保证海洋平台的快速准确定位。其中，全局搜索采用遗传算法，局部搜索则采用模拟退火算法。

由于海洋环境的不确定性，导致系统方程中的水动力参数具有严重不确定性，所以采用具有较强鲁棒性的保性能控制器来产生抵抗环境扰动的控制合力，其特点是对于所有允许的不确定性，闭环系统是渐近稳定的，并能保证闭环系统的性能指标不超过某个确定的上界［2］。考虑到平台主要受定常环境扰动的影响，这使得系统的稳态误差显著，因此在最优保性能控制器中引入积分作用来减小系统的稳态误差。

1 自动锚泊定位系统方案

半潜式平台对于风浪流作用下产生的水平运动不具有回复力，需要配备定位系统以平衡外力。为保证平台的作业性能及设备安全可靠，提出具有自动收放锚链及均衡锚链张力分布等功能的自动锚泊定位系统。图1为系统的原理框图，系统由积分型最优保性能控制器计算出在环境扰动作用下，平台定位到期望位置所需要的控制合力，张力优化算法将控制合力均匀分配给12条锚链，以保证锚链力场的均匀分布，同时将优化值作为锚链切换的阈值。随动机构通过控制锚链的收放来保证张力达到设定的阈值，从而使平台尽可能地保持在海平面上所要求的位置。

传统的自动锚泊定位系统采用12台锚机控制12条锚链的收放以产生张力来削弱海洋环境的干扰，将其改良为仅由4台三链轮卧式锚机分别对12根锚链进行切换控制。中央控制站同时向4台锚机发送指令，控制4条锚链的收放，即每台锚机的驱动装置只能与其中的一条锚链结合，而其余2条锚链处于切断状态。当与驱动装置所接合的锚链的张力达到优化方法所设定的阈值时，发送控制指令控制锚机驱动装置进行切换，与另一条锚链接合，继而控制所接合锚链的收放，直到到达理想的位置。这种控制方式在保证平台的定位精确度的基础上，降低了自动锚泊定位系统的总体成本，同时兼顾了锚链张力场的均匀分布，避免了因张力分配不均而引起锚链断裂的安全隐患。

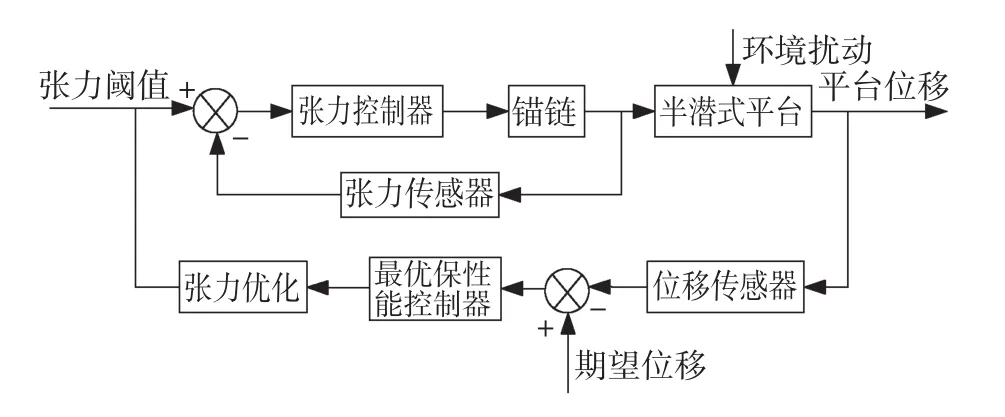
图1 锚泊自动定位系统原理Fig.1 Principle of Automatic Mooring Positioning System

2 锚泊定位系统保性能控制器设计

2.1 平台数学模型

半潜式平台在风浪流等海洋环境扰动作用下将产生高频往复运动及低频慢漂运动。高频运动只是影响到平台的运动姿态，对平台位移的影响很小，而低频运动是使平台漂离基准位置的主要因素。若对高频模型进行控制，会引起锚机响应频繁、锚链磨损加速及系统控制能量消耗增加等问题，因此仅考虑平台的低频运动模型。平台水平方向的控制模型一般可表示为

式中:η =［x，y，φ］T为固定坐标系下的平台纵荡位移、横荡位移及艏摇角度;v=［u，v，r］T为运动坐标系下相应的水平方向上的速度向量;R(ψ)为固定坐标系和运动坐标系间的旋转矩阵;M为质量矩阵;D为包括锚链阻尼及平台阻尼在内的总阻尼矩阵;τ=［Fx，Fy，Nz］T为锚链张力及低频环境扰动力在水平方向上的合力(力矩);b∈R3表示未建模的环境力(力矩)。为减少旋转矩阵中的耦合性，假设艏向角相对于期望值的变化不大，则可应用小角理论，非线性的旋转矩阵可近似的表示为一个单位矩阵［3］:=Rv≅Iv，基于此假设条件，式(1)可转化为如下的状态空间形式:

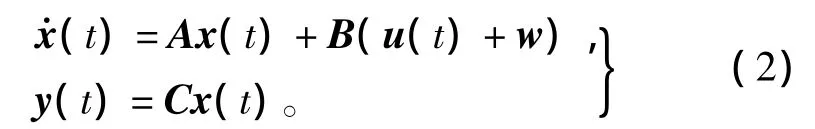
式中:x=［vT，ηT］T为状态向量，u(t)为水平方向上控制力(力矩)的合力(力矩);W为三维扰动向量，包括稳流风、隶属于低频范围内的湍流风、海流及波浪漂移载荷;y是平台位置和艏向角的观测向量。系数矩阵

由于海洋环境的不确定性，使得平台运动方程中的质量及阻尼矩阵具有严重的不确定性［4］，同时考虑到平台主要受到可视为定常扰动的稳流风，流及二阶波浪力作用，使得系统的稳态误差显著，因此在模型中引入能有效减小稳态误差的积分作用形成增广空间，计入不确定性及积分作用的平台自动锚泊定位系统控制模型可以表示为

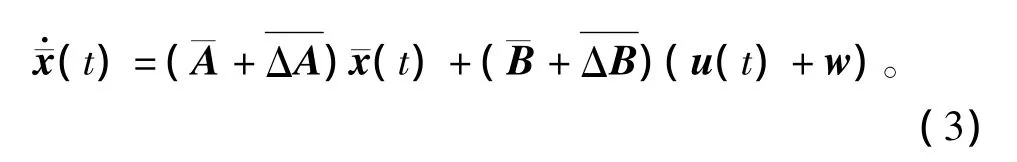
2.2 最优保性能控制

保性能控制是研究不确定系统的一种重要的鲁棒控制方法，运用保性能控制可以保证对于所有允许的不确定性，闭环系统是渐进稳定的，并具有一定的鲁棒性。针对式(3)所表示的不确定性系统，假设所考虑的参数不确定性是范数有界的，且具有以下形式［5］:

式中:D，E1，E2为适当维数的已知常数矩阵，反应了不确定性的结构信息，F(t)∈Ri×j是一个未知矩阵，它可以是时变的，且满足:F(t)∈ΩF:={F(t):‖F(t)‖≤I}，针对系统(3)，定义二次型性能指标:

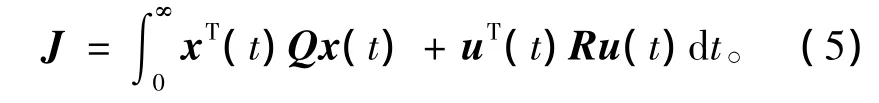
对于系统(3)和性能指标(5)，如果存在一个控制律u(t)和一个正数J*，使得对于所允许的不确定性，闭环系统是渐进稳定的，且闭环系统性能指标满足J≤J*，则J*为不确定系统(3)的一个性能上界，u(t)为不确定系统的一个保性能控制律。如何选取一个适当的控制律使得系统性能指标最小，即为最优保性能控制，具体过程如下:

定理1 对给定的系统(3)及性能指标(5)，如有以下优化问题:

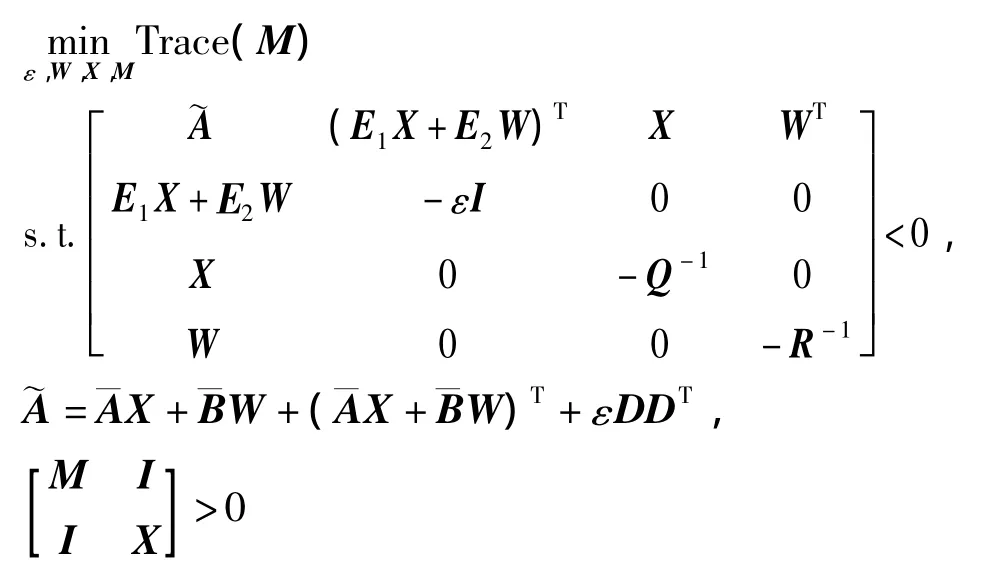
证明过程略，参照参考文献［5］。

由最优保性能控制计算出使平台定位到期望位置所需的控制力(力矩)，需张力优化算法将控制合力均匀分配给12条锚链，以保证锚链力场的均匀分布，同时将优化值作为锚链切换的阈值。

3 锚泊定位系统张力优化

3.1 优化模型

锚泊自动定位系统应通过对锚链的收放，使平台尽可能保持在目标位置，并能同时保证各锚泊张力的均匀分布。锚链张力的均匀分布对于防止锚链断裂，保证海洋平台的安全具有重要意义［6－7］。因此，目标是在保证平台目标位置的基础上优化锚链的张力分布，结合锚泊系统模型，定义目标函数为各锚链张力差的平方和，即

约束条件为

其中:Fx和Fy分别为横荡及纵荡方向上的海洋环境扰动力;M为艏摇方向的海洋干扰力矩;Ti为各锚链的张力值;φi为锚链的布置角度;θi为着缆点与平台中心的连线和x轴的夹角;di为着缆点到平台中心的距离;K是锚链的安全因子，根据API RP－2SK规定，其一般大于1.67［8］。约束条件中的等式约束用来保证海洋平台的位置，而不等式约束则用来保证锚链的安全性。

3.2 混合优化算法总体框架

所提出的自动锚泊定位方案是以张力的均匀分布为基础，优化方法的效率和精确度将直接影响整个系统的运行速度和定位精确度，而传统的优化方法则存在各自的局限性，因此将遗传算法和改进的模拟退火算法结合形成混合搜索策略来提高优化效率［9］，保证海洋平台的快速准确定位。

遗传算法全局搜索能力强，但进化后期收敛速度慢;而模拟退火算法局部搜索能力强，运行时间较短，求解精确度高。因此，为提高自动锚泊定位系统的整体运行速度，保证锚链张力的均衡分布及海洋平台的定位精确度，借鉴Memetic算法思想将遗传算法与模拟退火算法相结合。混合优化基本流程的伪码描述为:

Procedure general MA

begin

for i=1 to p－size do

initialize p(t);

evaluate f(xi);

endfor

if SA is applied then

add the ε largest fitness individuals to EP;

apply SA upon each individual of EP;

endif

do until a termination condition is reached

selection;

crossover;

mutation;

update p(t);

for i=1 to p－size do

update p(t):add EP to p(t)and replace the small fitness individuals with EP;

endfor

select for next generation

enddo

end

其中p－size表示种群个体数，EP表示具有高适应度个体的精英集合。如上面流程所示，这种混合算法仍是从一个随机产生的初始种群开始，然后利用遗传算法从种群中选择适应度较高的精英集合进行局部改进，执行模拟退火算法，直到满足终止条件为止。

3.3 改进模拟退火算法

模拟退火算法中，随机搜索变量的产生方式，初始及终止温度的选取，接受概率及冷却函数均是影响寻优速度的关键因素［10］。在每代进化中引入精英集合EP(‖EP‖≪p－size)，仅对EP中的个体进行SA局部搜索。同时对标准SA算法进行改进以提高搜索寻优效率:由混沌遍历搜索确定初始温度，以便消除高温阶段的冗余迭代;由一维logistic混沌遍历搜索代替随机搜索。用一维logistic映射产生混沌变量，即

确定初始温度

其中:fmin及fmax分别为初始种群中最大及最小适应度值;pr为最差初始接受概率。如此可通过pr来调整初始温度，避免过高初温对寻优速率的影响及过低初温对优化质量的影响。同时用线性变换将logistic产生的混沌向量映射到锚泊线张力分配的状态空间中，并对其采用混沌遍历搜索作为SA算法中的搜索策略。

4 仿真结果及分析

对半潜式海洋平台在一年一遇海洋环境扰动下的纵荡运动进行仿真研究。为了有效利用Matlab中LMI工具箱，半潜式平台采用无因次参数描述，在系数矩阵A，B的基础上，由于积分作用的引入，需对系数矩阵进行增广，增广之后如考虑3自由度运动，则系数矩阵A是9维方阵，为节约篇幅，仅给出纵荡运动设计过程参数，其他两个自由度具有相同的过程。

系统性能指标(5)的加权矩阵为

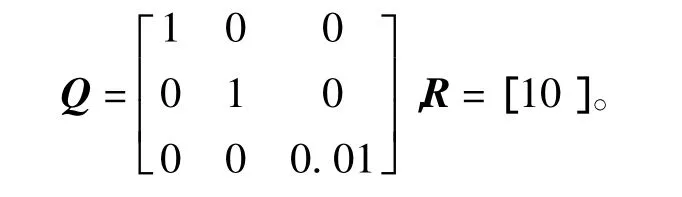
根据定理1，求解矩阵不等式，可得

图2 纵荡方向的合力Fig.2 Force in surge direction

目标平台的作业水深为1 500 m，锚泊系统采用链－缆－链分段组合形式，共12根，布置方式如图3所示。考虑风、浪、流方向相同的最不利工况(以海洋环境载荷以45°方向作用于平台为例)。

图3 锚链布置示意Fig.3 Distribution of mooring lines

令初始种群规模为200，在遗传算法的选择操作中应用精英保留策略，即通过适应度函数对个体进行评价排序，适应度较高的个体(本文中选取20%)进行局部改进，执行模拟退火算法。遗传算法交叉概率0.7，变异概率0.02，精英保留个数40，进化代数200。模拟退火算法中初始温度500℃，温度下降参数0.85。分别采用遗传算法及混合优化算法对12根锚链的张力分配进行优化。优化结果如表1及图4所示。

优化结果表明，混合优化算法相对于传统遗传算法更适合于本文提出的基于锚链张力优化值作为切换阈值的海洋平台自动锚泊定位系统的设计，因为其具有更快的收敛速度及更高的优化精度，能够保证海洋平台的快速准确定位，平台纵荡方向的位移如图5所示。

图4 两种优化方法进化进程Fig.4 Evolution process of two optimization methods

表1 两种优化方法优化结果Table 1 Optimization results of two methods

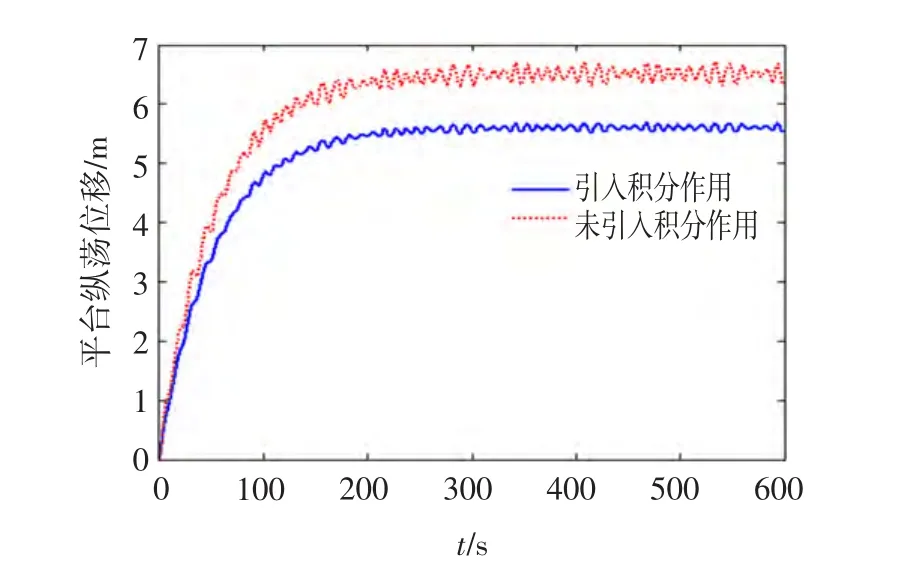
图5 平台纵荡位置仿真结果Fig.5 Surge simulation results of the platform

由图可知，引入积分作用的最优保性能控制有效减小了稳态误差。但引入积分作用后，仍存在一定的稳态误差(期望位置为纵向5 m处)，一方面是由于作为锚链切换阈值的张力优化结果存在一定的允许误差，致使张力的合力不恒等于零而引起的位移偏差;另一方面，环境扰动中的高频一阶干扰力所引起的误差:为了避免锚机动作频繁，锚链的磨损加速及控制能量消耗增加等现象，仅对低频扰动进行控制，尽管控制过程中不计入高频的一阶干扰力，但其作为环境扰动是真实存在的，在理想情况下，高频一阶扰动是均值为零的随机过程，但在一段时间内，其均值存在不等于零的情况，引起一起部分误差。虽然方案存在一定的误差，但其充分满足平台的作业要求，并能均衡锚链力场的分布，保证了海洋平台工作的安全性。

5 结论

本文提出了一种基于锚链切换控制的自动锚泊定位新方案。利用保性能控制在处理参数不确定性方面的优势，设计了改进最优保性能控制算法，解决了由于海洋平台运动模型的不确定性对系统设计造成的困难，同时所设计的控制器由于积分作用的引入，减小了系统的稳态误差。张力优化方面，利用遗传算法和模拟退火算法的互补性，以实现各锚链张力值方差最小为目标函数，构造混合算法来优化锚链的张力分布以使其受力均衡，防止单根锚链因受力过大而断裂，并将优化结果作为锚链切换的阈值。优化结果表明，混合优化算法具有更快的收敛速度及更高的优化精确度，更加适用于本系统设计。整体仿真表明，提出的方案能够保证海洋平台的定位要求，并能兼顾锚链力场的均匀分布。同时，由于锚链切换控制的加入，使得该锚泊定位系统仅采用4台三链轮锚机即可实现原有12台锚机的功能，降低了系统的总体成本，保证了经济性。

［1］BERNTSEN P I，LEIRA B J.Ensuring mooring line integrity by dynamic positioning:Controller design and experimental tests［J］.Automatica，2009，1285 －1290.

［2］马闯，李清华，伊国兴，等.大延时网络化控制系统保性能控制［J］.电机与控制学报，2008，12(1):104 －108.MA Chuang，LI Qinghua，YI Guoxing，et al.Guaranteed cost control for networked control systems with large time delays［J］.Electric Machines and Control，2008，12(1):104 －108.

［3］GARRETT D.Coupled analysis of floating production systems［J］.Ocean Engineering:2005，32(7):802－816.

［4］SORENSEN A.Structural issues in the design and operation of marine control systems［J］.Annual Reviews in Control，2005，29(1):125－149.

［5］俞立.鲁棒控制——线性矩阵不等式处理方法［M］.北京:清华大学出版社，

［6］LOTFI K G，SHERIFA M，ASHRAF O N.A particle swarmbased genetic algorithm for scheduling in an agile environment［J］.Computers＆ Industrial Engineering，2008，55(3):707－720.

［7］SHAFIEEFAR M，REEZVANI A.Mooring optimization of floating platforms using a genetic algorithm［J］.Ocean Engineering，2007，34:1413－1421.

［8］严传续，钱宏，项军毅，等.铺管船锚泊定位系统优化设计研究［J］.中国造船，2010，51(1):84 －93.YAN Chuanxu，QIAN Hong，XIANG Junyi，et al.Study on design optimization of mooring positioning system for pipelaying vessel［J］.Shipbuilding of China，2010，51(1):84 －93.

［9］GALLARDO J E，COTTA C，FERANDEZ A J.On the hybridization of memetic algorithms with branch-and-bound techniques［J］.IEEE Transactions on Systems，Man，and Cybernetics－ Part B，2007，37(1):77－83.

［10］张军，张侃谕，周强.基于改进模拟退火算法的多台冷水机组负荷优化分配［J］.农业机械学报，2012，43(3):187－19.ZHANG Jun，ZHANG Kanyu，ZHOU Qiang.Improved simulated annealing algorithm in optimal load distribution of multiple chillers for energy conservation［J］.Journal of Agricultural Machinery，2012，43(3):187－19.