模块组合式定子永磁电机边端力分析及削弱方法

张炳义， 贾宇琪， 冯桂宏

(沈阳工业大学电气工程学院，辽宁沈阳110870)

0 引言

近年来，低速大功率永磁电机直接驱动技术在矿山、石油、冶金、船舶推进以及风电等机械装备中得到了越来越广泛的关注。低速大功率电机一定具备低速大转矩电机的特点，而电机的转矩又与电机的有效体积成正比，因此低速大功率直驱永磁电机的体积势必很庞大。电机过大的体积会给其制造、运输、装配以及维护带来巨大的困难。在一些例如军用、航天、船舶推进等对设备运行可靠性要求高的领域，即使驱动系统出现故障，也要求维持驱动系统部分功能或保证重要部件能够继续运行，这就对电机驱动系统提出了故障后容错的要求。为此，本文提出了一种基于采用不等跨距绕组的模块组合式定子永磁电机结构(permanent magnet synchronous machine with module combination Stator，MCS － PMSM)，实现了交流电机定子的模块化制作，从一定程度上能够缓解大型交流电机定子过大带来的相关问题。为了满足该种电机装配、固定及故障拆卸维修需要，相邻定子模块之间需要留有一定的缝隙，而该缝隙的存在会导致定子模块边端磁导的突变，引起边端效应。为了改善电机运行的平稳性和控制精确度，本文对MCS－PMSM中的边端力进行了分析。

目前，为了减小推力波动，提高伺服精确度，国内外学者进行了大量的研究，主要形成了两种方法，一种是改进优化电机结构，另外一种是通过控制补偿抑制推力波动［1］。例如，文献［2］在采用二维有限元对电机静态推力分析的基础上，通过能量法推导了电机的推力公式;文献［3］则采用基于标量磁位分离变量法解析求解了径向充磁圆筒永磁直线同步电机磁场;徐同月等［4］通过优化电机动子长度方法降低边端力，极大地减少了PMLSM的推力波动，提高了其伺服控制精确度;Kok等［5］采用滞后的继电反馈控制方法，对推力波动和摩擦力扰动进行了补偿，改善了跟踪性能;文献［6］提出了一种直线电机采用圆角平滑过渡结构来减缓磁导的突变，进而降低边端力;文献［7］采用将动子两边端的齿降低一定高度的方法来降低边端力;文献［8］依据电磁场理论对长初级DSLIM的动态纵向边端效应进行了分析，导出了电机的等效电路模型及其修正系数;文献［9］采用有限元法对电机的齿槽力和边端力进行了仿真分析，并根据仿真结果对改型电机的推力波动进行了优化;文献［10］从理论分析、数字仿真的角度研究了电机极数及边端铁心对电机静态纵向边端效应的影响机理;文献［11］研究了弧形永磁电机转矩波动的削弱方法。

综上可以看出，现有文献对电机边端力的研究主要集中在直线电机上面，对于本文提出的MCSPMSM结构则鲜见报道。因此，本文将重点分析MCS－PMSM力矩波动的来源和边缘效应，并利用Schworz－Christistoffel变换方法，求解了气隙相对磁导函数，进而得到定子模块边端处的气隙磁场分布，最后采用基于定子模块宽度优化和定子铁心轴向错位结构两种方法对定子模块边端力进行了分析和削弱研究。

1 MCS-PMSM样机结构和参数

MCS－PMSM样机基本结构如图1所示，图中所示电机定子以8个单元模块组成为例，转子结构与常规永磁电机基本相同。为了能够形成三相对称绕组，每个定子模块内嵌放着由大、小两种跨距规格线圈构成的不等跨距绕组，并且通过采用大跨距线圈反向嵌放的方法实现三相绕组在每个定子模块内的独立放置，不等跨距绕组结构如图2所示。设计出MCS－PMSM样机的主要参数见表1。

图1 MCS－PMSM样机模型Fig.1 Prototype model of MCS-PMSM

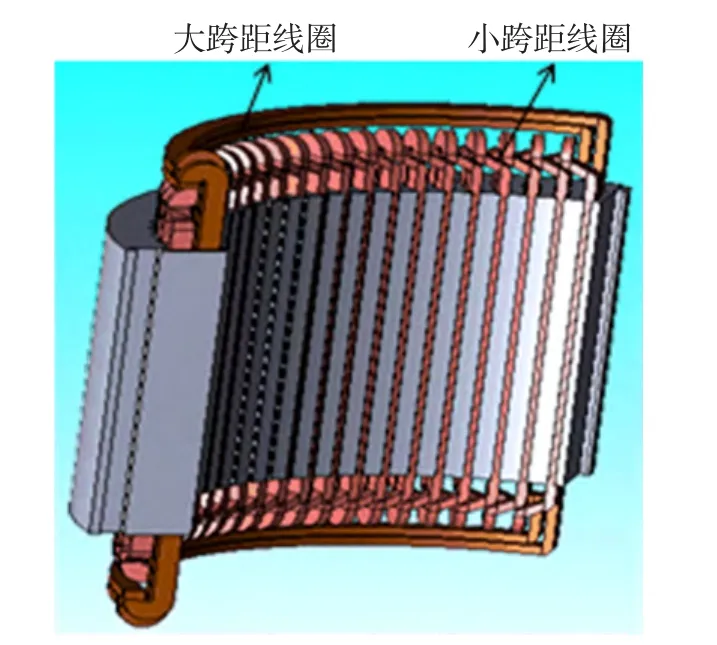
图2 不等跨距绕组结构图Fig.2 View of Unequal span winding

MCS－PMSM的突出优势在于当电机某个或者某几个单元模块发生故障时，电机仍然能够降功率维持运行，这显然提高了电机本身的可靠性和容错能力。考虑到电机每个定子模块装配、固定以及维修的需要，电机相邻定子模块之间需要留出一定的缝隙，MCS－PMSM装配示意如图3所示。主要研究相邻定子模块之间缝隙的存在而引起MCSPMSM中单个定子模块的边端效应和所受到的边端力。由于每个单元模块都相同，因此后续对定子模块受到边端力的分析只任意选取其中的一个模块进行。

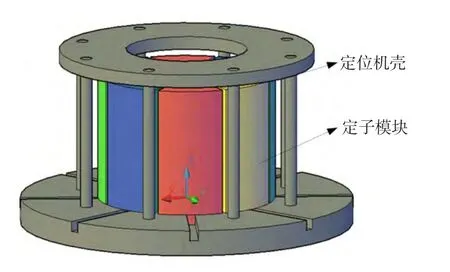
图3 MCS－PMSM装配示意Fig.3 Assembly sketch map of MCS-PMSM

2 MCS-PMSM力矩波动来源与边端效应分析

2.1 MCS-PMSM力矩波动来源分析

MCS－PMSM在某种程度上可以看作是由标准的直线电机弯曲而成，而直线电机的推力为

式中:N为线圈匝数;lef为铁心计算长度;Bm为气隙磁密的幅值;Im为相电流幅值。

从式(1)可知，理想情况下电机的电磁推力正比于电流幅值和气隙磁密基波幅值，当电流幅值和气隙磁密基波幅值为常数时，推力就保持恒定，不存在波动。但是实际中，由于制造公差和装配工艺等因素的影响，导致电机绕组中的电流和气隙磁密不是完全的正弦波，而是存在一系列谐波;另外，再加上电机结构存在一些不随电流存在而存在的力矩，如齿槽力矩和边端力矩等，电机运行过程中，齿槽力矩和边端力矩会附加在电磁力矩上引起电机的转矩波动，从而引起电机的电磁推力不为恒值。关于齿槽力矩的分析已有众多文献，因此重点分析MCSPMSM的边端力。

2.2 基于Schworz-Christistoffel变换边端效应分析

MCS－PMSM的边端模型如图4所示，采用Schworz－Christistoffel变换进行分析前，作以下假设:

1)定子铁心为无限长，无限高;

2)定子铁心磁导率无穷大，其表面为等磁位面，一面磁位是0，一面磁位是φ0;

3)转子铁心表面光滑。

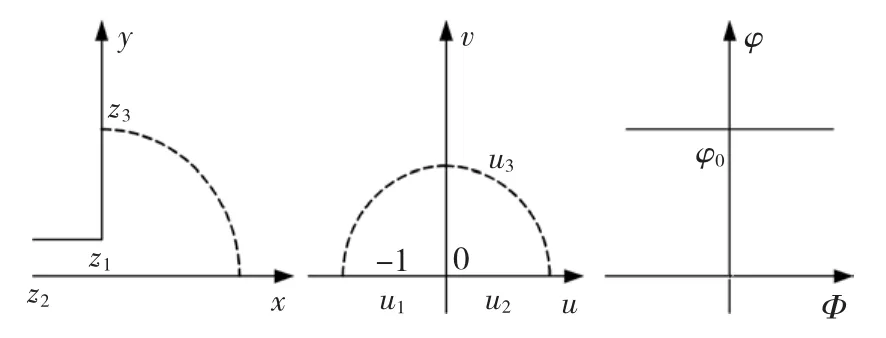
图4 边端效应Schworz－Christistoffel变换模型Fig.4 Schworz-Christistoffel transformation model of MCS-PMSM end effect

对应上图的 Schworz－Christistoffel变换为［12］

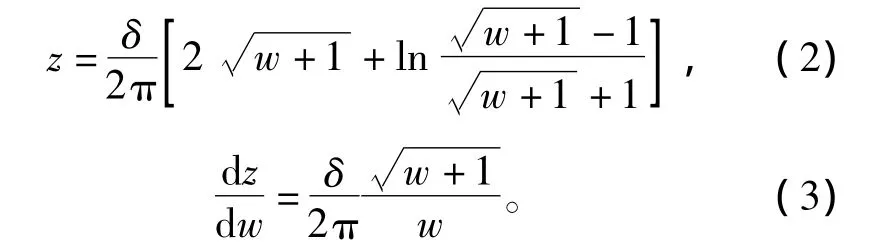
式中，δ为定子与转子之间的气隙高度。

从w平面到t平面的变换为

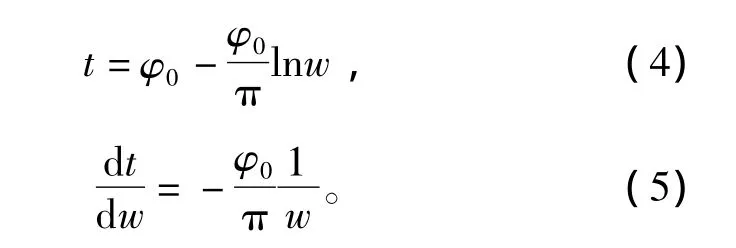
于是，电机端部任意一点处的磁感应强度为

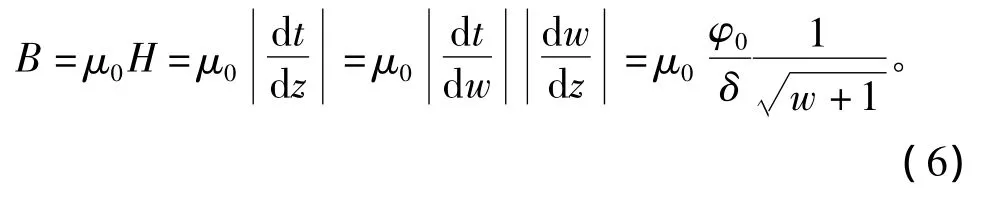
将z=x，w=u代入到式(11)，得到 x－B的关系

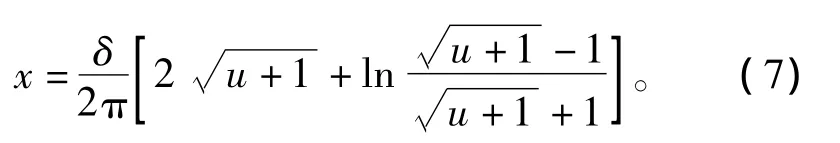
综上，得到的MCS－PMSM定子边缘处磁感应强度随位移变化如图6所示。同时，为了验证采用Schworz－Christistoffel变换方法的合理性，也采用有限元方法进行了仿真分析，模型如图5所示。分析区域位于2个定子模块铁心的中间开断部分(缝隙宽度bf=4 mm)，通过提取该区域气隙中心线沿圆周方向分布的磁感应强度的幅值，进而求得该区域的磁感应强度随定子边缘处距离变化的关系。

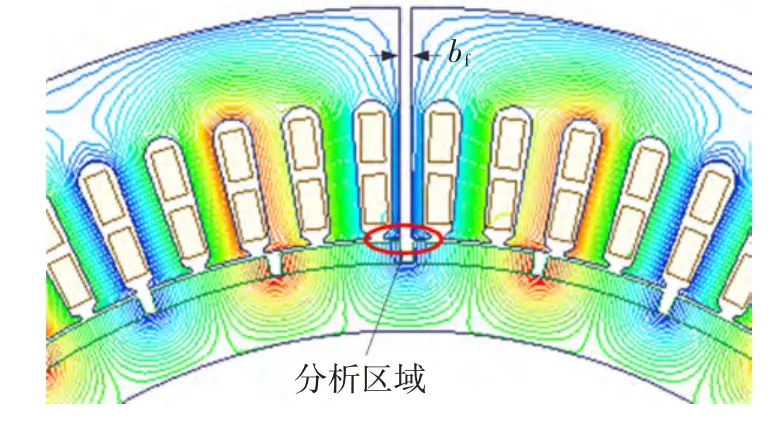
图5 边端效应有限元分析模型Fig.5 FEM analysis model of end effect

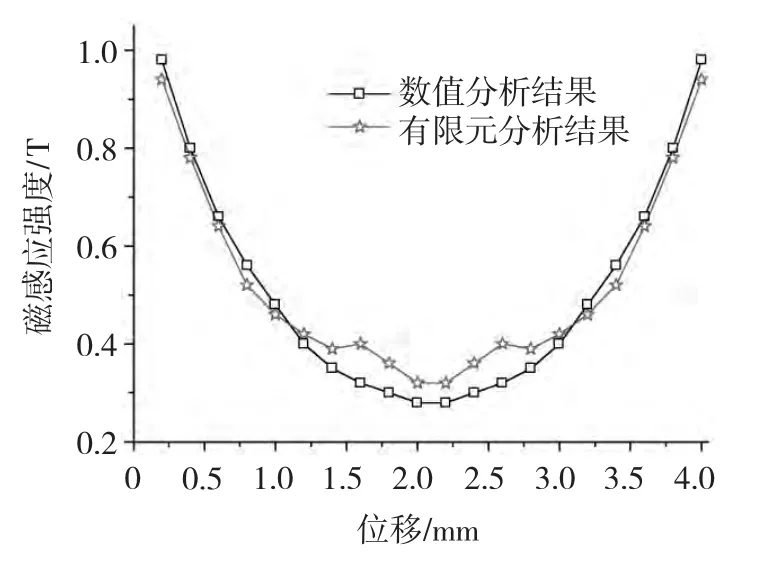
图6 磁感应强度随定子边缘处距离变化Fig.6 Module stator edge magnetic induction intensity change with displacement

通过图6中数值分析结果和有限元分析结果的对比，可以看出采用两种方法求得的电机定子边缘处磁感应强度波形基本一致，从而很好地证明了采用Schworz－Christistoffel变换方法的合理性。两种方法分析结果中存在的误差主要是由于数值解析方法的前提假设引起。

3 MCS-PMSM边端力削弱方法研究

3.1 基于定子模块宽度优化的边端力削弱方法

从以上分析可知，定子边端磁导的突变导致了边端力的产生。根据文献［13］可知，通常情况下单元模块定子宽度为2～3倍极距，单个模块两边端之间基本上没有相互影响。定子模块两端受到幅值大小相同，但方向相反的边端力的作用，且两者存在一个相位差，而该相位差的大小取决于定子的宽度。因此，可以通过优化定子宽度的方法来使左右两端的边端力相互抵消，从而降低电机的力矩波动。文献［14］分析认为，若两端所受的边端力相位差为(2k－1)π，则左、右边端力能够完全相互抵消，从而使整个铁心模块受到的合成边端力为零。但是由于实际中边端力的谐波成份复杂，而且铁心模块的几何相位差和两个边端力的相位差并不一致，所以不能直接利用这个方法来优化定子模块的宽度。以下采用分析左、右两个边端力谐波成份来寻找减小边端力的方法。

从上述分析，有

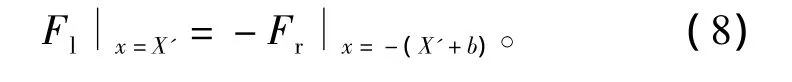
式中:Fl、Fr分别为定子铁心模块所受的左、右边端力;b=kτ为定子模块沿圆周方向宽度;τ为极距;k为任意整数。

将左边端力展开为傅立叶极数，有

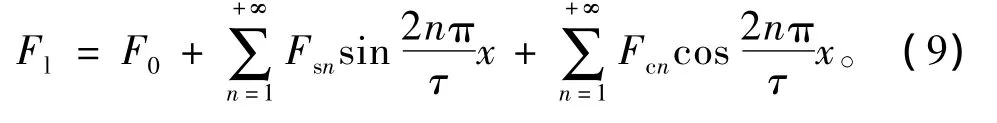
由式(8)、式(9)，得

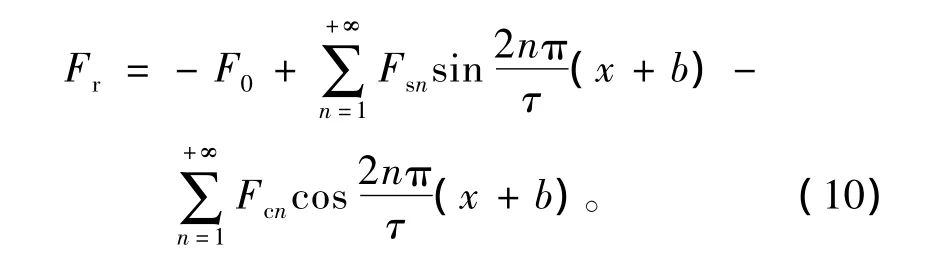
合成边端力可以看作为左、右两个边端力的合力，即

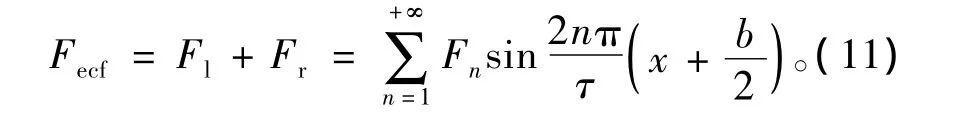
其中:

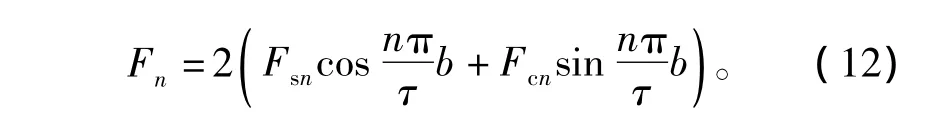
显然，要使Fecf最小，可以令系数:

综上，求得使Fecf最小的b值，为

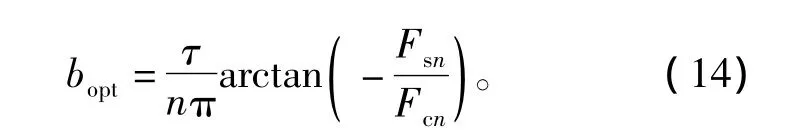
但是，由于边端力Fecf中包含了各阶谐波分量，因此无法使Fecf各次谐波系数都为0，而只能使Fecf尽量达到最小。分析边端力中各次谐波成份所占的比重，不难发现基波成份最大。因此，能使Fecf达到最小的b值为

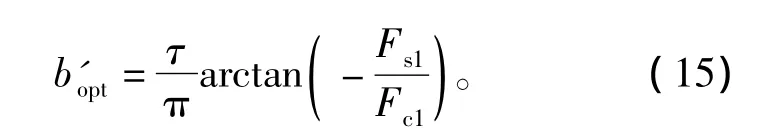
通过有限元方法来计算定子模块的最优宽度。原型样机初始定子宽度为4倍极距，即单个模块所占机械角度为45°。为了防止齿槽力对电机边端力分析造成影响，模型中定子铁心为无齿槽结构，如图7所示。分析过程中，定子模块保持不动，转子以65°/s的机械角速度转动，得到的定子模块左、右边端的边端力如图8所示。

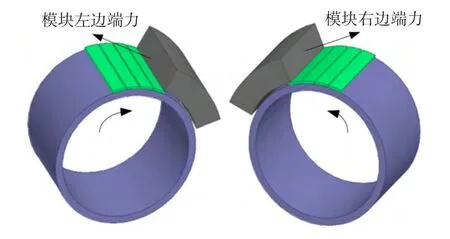
图7 单个定子模块左、右边端力分析模型Fig.7 Left and right end cogging force FEM Analysis model of single module stator

从图8看出，模块定子的左、右边端力都呈现明显的周期规律，且最小周期为

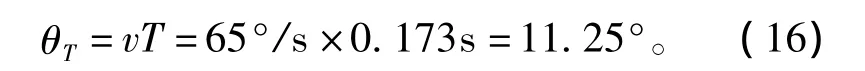
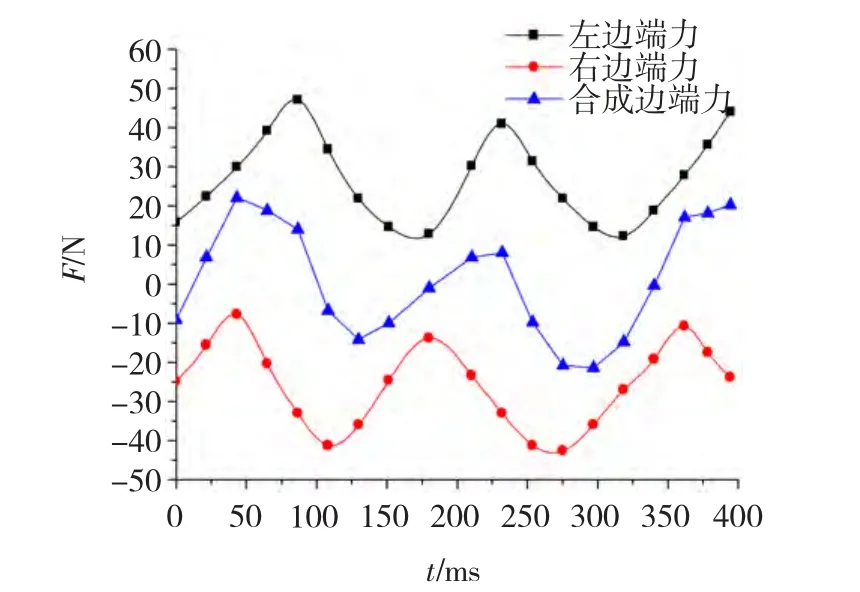
图8 单个模块定子左、右边端力仿真结果Fig.8 Simulation result of left end cogging force and right cogging end force by FEM

也就是说边端力都是以电机极距为周期波动，这与前面的分析结果相吻合。下面采用多阶傅立叶极数对得到的左、右边端力进行回归分析，有

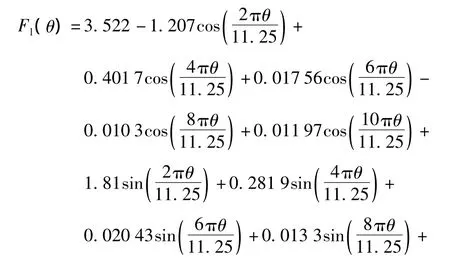
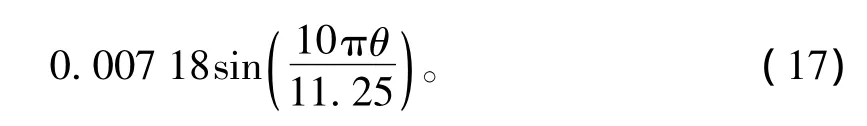
根据式(15)、式(17)，得

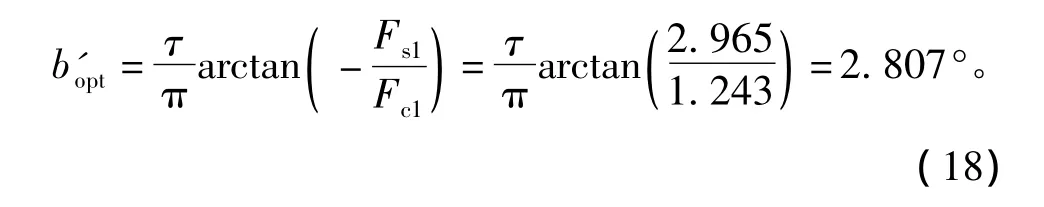
另外，从图8仿真结果还可以发现，左、右边端力存在一个相位差，使得左边端力为最大时右边端力并非最小，并且该相位差与模块定子的宽度相关。试想，若在现有定子宽度的基础上减小一定的宽度，就可以实现模块定子左、右边端力之间的相位互差180°，进而就可以最大程度的削弱合成边端力。显然，图中左、右边端力峰值之间的时间差是43.27 ms，于是定子模块宽度应该减小角度:

从式(18)、式(19)看出，采用两种方法计算得到的定子铁心模块的宽度优化结果基本相同。最终电机的定子宽度应为

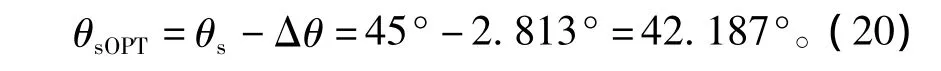
考虑到加工制造方便，实际中可以取电机定子宽度为42.2°。优化后与优化前的模块定子合成边端力如图9所示。

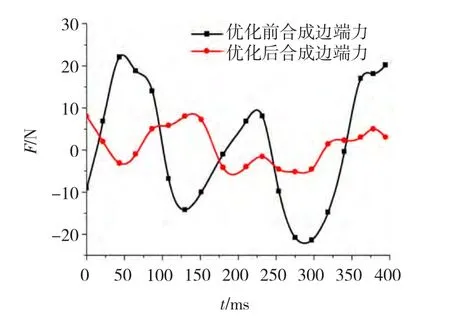
图9 优化前后模块定子合成边端力对比Fig.9 Synthesis result of left end cogging force and right end cogging force before and after optimization

从图9看出，电机定子模块宽度没有优化时，其合成边端力有效值为26.87 N·m，优化后的合成边端力仅为7.29 N·m。从优化结果可以看出，基于定子宽度优化减小模块定子边端力方法对于削弱定子边端力效果还是比较明显的。另外，从装配的角度说，该方法在减小模块定子边端力的同时，也为相邻模块之间留出了更大的缝隙，而该缝隙是电机装配、固定及拆卸维修所必需的。

3.2 基于定子铁心轴向错位结构的边端力削弱方法

如前所述，定子模块宽度的大小决定了其所受到的左、右边端力之间相位差的大小。试想，如果定子模块铁心采取轴向分段错位结构，那么定子模块所受到的单侧边端力会因错位尺寸的不同而产生一个相应的相位差。因此，如果错位尺寸选取合理，使的定子模块铁心单侧不同错位部分受到的边端力相位相差一定的相位，则同样能够起到削弱边端力的作用。下面以定子铁心轴向两段错位结构受到的右边端力为例来进行计算说明。

定子铁心轴向错位结构如图10所示。采用同样的分析方法，即保持定子模块不动，转子以65°/s的机械角速度逆时针转动，来分析轴向两段错位铁心结构的右边端力，结果如图11所示。

从图11可以看出，采用定子模块铁心轴向两段错位结构后，定子模块受到的右边端力从优化前的33.58 N·m降至优化后的26.43 N·m，并且波动幅度大幅度降低。优化结果标明，采用定子铁心轴向错位方法亦能够从一定程度上减小定子模块所受边端力，大幅度缩小其波动幅度。

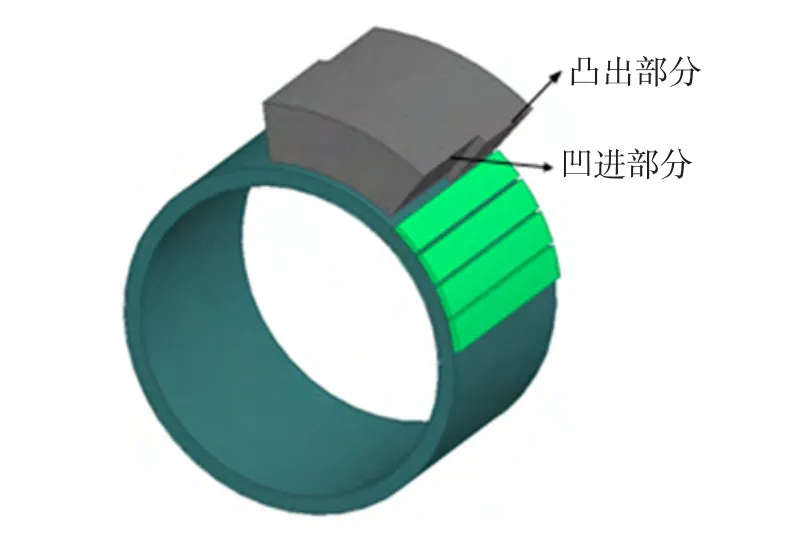
图10 定子铁心轴向两段错位结构示意Fig.10 Structure of module stator core adopting two section axial dislocation

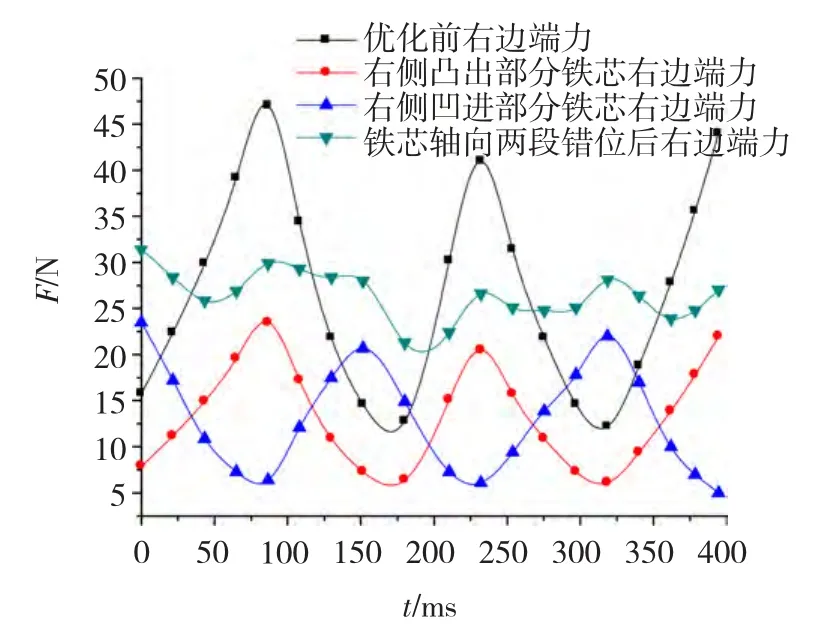
图11 定子模块铁心轴向两段错位结构右边端力仿真结果Fig.11 Simulation result of right end cogging force with Structure of module stator core adopting two section axial dislocation

4 结论

针对低速大功率电机过大的体积给其制造、运输、装配以及维护带来不便和可靠性低等问题，本文提出了一种基于采用不等跨距绕组结构的MCSPMSM结构，实现了低速大功率电机定子的模块化制作，从一定程度上缓解了低速大功率电机定子过大带来的相关问题，从而增强了电机的制造灵活性、运行可靠性以及可维护性，提高了电机运行的可靠性和容错性。为了提高模块组合式定子永磁电机运行的平稳性和控制精确度，分析了MCS－PMSM力矩波动的来源，重点对模块化定子的边端效应进行了研究。指出相邻模块之间存在装配、固定及故障维修所必需的缝隙引起定子边端的磁导突变是产生边端力的主要原因。定子模块两侧的边端力大小基本相同，方向相反，明显具有周期性。最后研究了采用定子模块宽度优化和定子模块铁心轴向错位结构两种途径削弱合成边端力。分析结果表明了两种方法对于减小模块定子边端力的有效性。研究内容为实现MCS-PMSM的高精度控制提供了一定的参考依据。

［1］陆华才，江明，郭兴众，等.永磁直线同步电机推力波动约束［J］.电工技术学报，2012，27(3):128－132.LU Huacai，JIANG Ming，GUO Xingzhong，et al.Thrust ripple suppression for permanent magnet linear synchronous motor［J］.Transactions of China Electrotechnical Society，2012，27(3):128－132.

［2］黄磊，余海涛，胡敏强，等.用于电磁弹射的容错性初级永磁直线电机特性［J］.电工技术学报，2012，27(3):119－127.HUANG Lei，YU Haitao，HU Minqiang，et al.Characteristics of a primary permanent magnet linear machine with fault－tolerant capability for electromagnetic launch［J］.Transactions of China Electrotechnical Society，2012，27(3):119 －127.

［3］赵镜红，张俊洪，方芳，等.径向充磁圆筒永磁直线同步电机磁场和推力解析计算［J］.电工技术学报，2011，26(7):154－160.ZHAO Jinghong，ZHANG Junhong，FANG Fang，et al.Analytical calculation of magnetic field and thrust force in radial magnetized tubular permanent magnet linear synchronous motor［J］.Transactions of China Electrotechnical Society，2011，26(7):154－160.

［4］徐月同，傅建中，陈子辰.永磁直线同步电机推力波动优化及实验研究［J］.中国电机工程学报，2005，25(12):112－115.XU Yuetong，FU Jianzhong，CHEN Zichen.Thrust ripple optimization and experiment for PMLSM［J］.Proceedings of the CSEE，2005，25(12):112－115.

［5］Si Lu CHEN，Kok Kiong TAN，Sunan HUANG，et al.Modeling and compensation of ripples and friction in permanent－magnet linear motor using a hysteretic relay［J］.IEEE/ASME Transaction on Mechatronics，2010，15(4):586 －594.

［6］潘开林.永磁直线电机的驱动特性理论及推力波动优化设计研究［D］，浙江:浙江大学，2003，24－32.

［7］Yu Wu Zhu，Sang Gun Lee，Koon Seok，et al.Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM［J］.IEEE Transactions on Magnetics，2009，45(6):2863－2866.

［8］鲁军勇，马伟明，李朗如.高速长初级直线感应电动机纵向边端效应研究［J］.中国电机工程学报，2008，28(30):73－78.LU Junyong，MA Weiming，LI Langru.Research on longitudinal end effect of high speed long primary double－sided linear induction motor［J］.Proceedings of the CSEE，2008，28(30):73－78.

［9］薛志强，罗雷，周羽.永磁直线无刷直流电机推力波动仿真分析及削弱方法［J］.船电技术，2010，30(5):11－17.XUE Zhiqiang，LUO Lei，ZHOU Yu.Simulation of thrust ripple of PM linear brushless DC motor and its minimization［J］.Marine E-lectric＆ Electronic Engineering，2010，30(5):11－17.

［10］孙兆龙，马伟明，鲁军勇，等.长初级双边直线感应电动机静态纵向边端效应及阻抗矩阵研究［J］.中国电机工程学报，2010，30(18):72－77.SUN Zhaolong，MA Weiming，LU Junyong，et al.Research of static longitudinal end effect and impedance matrix for long primary double-sided linear induction motors［J］.Proceedings of the CSEE，2010，30(18):72－77.

［11］Chang Jiu jian，Wen li Ma，Yong Kun Fan，et al.New methods for arc permanent magnet linear synchronous motor to decrease torque ripple［J］.IEEE Transactions on Magnetics，2012，48(10):2659－2663.

［12］K C LIM，J K WOO，G H KANG.Cogging force minimization techniques in permanent magnet linear synchronous motors［J］.IEEE Transactions on Magnetics，2002，38(3):1157 －1160.

［13］G.KREBS，A.TOUNZI，B.PAUWELS.Modeling of a linear and rotary permanent magnet actuator［J］.IEEE Transactions on Magnetics，2008，44(11):4357 －4360.

［14］ZHU Z Q.Reduction of cogging force in slotless linear permanent magnet motors［J］.IEEE Transactions on Magnetics，1997，144(4):277－282.