一种风电场HAPF后向线性谐波电流预测方法
李圣清, 张彬, 匡洪海, 徐天俊, 杨峻
(湖南工业大学电气与信息工程学院,湖南株洲412007)
0 引言
风电场中许多类型的分布式发电电源受制于自然条件,运行不确定性强,具有间歇性、复杂性、多样性及不稳定性特点,其电能质量特征与传统电力系统有很大差异[1-3],给谐波电流治理带来了较大的困难。对谐波电流进行跟踪和预测,然后根据预测值进行补偿,对解决谐波补偿延时问题起到了积极地作用[4-13]。从预测时间顺序角度考虑,谐波预测方法分为前向预测和后向预测两大类型,前向预测是根据x(k-1),x(k-2)…,x(k-m)之值预测 x(k)值。相应地,由x(k-m+1),x(k-m+2)…,x(k)之值预测 x(k-m)值,就称为后向预测[4]。尽管人们对前向预测有比较深入的研究,但后向预测问题几乎无人问道。文[14]选用一种模型预测控制策略,根据有源电力滤波器(active power filter,APF)实际输出与预测输出间的误差进行反馈校正和滚动优化,克服了系统的不确定性,提高了APF的谐波电流补偿特性。不足之处是系统计算较为复杂,不利于实际操作。文[15]提出一种基于灰色模型的无时延预测控制方法,并将其成功应用于并联型混合有源电力滤波器(Hybrid active power filter,HAPF)控制中,具有一定的谐波抑制和无功补偿性能,但是系统预测精度与稳定性有待于提高。文[16]提出了一种新型三相并联型APF的径向基函数神经网络预测控制方法,建立三相四线制并联型APF的数学模型及电流预测控制的离散化模型,设计神经预测控制器,具有较好的稳定性,但是动态响应特性有待于提高。
本文提出了基于后向最佳线性预测理论的风电场HAPF谐波电流预测方法,能根据现在时刻的谐波电流,预测出前面时刻的谐波电流,响应速度快,预测精度高,为对其展开分析和评估及制定后续谐波电流控制方法提供强有力的依据。
1 风电场HAPF工作原理
传统的HAPF装置直流侧储能元件一般为电容器,在快速跟踪风电场谐波电流时,逆变器产生的开关损耗会引起电容器上的电压波动,使直流侧出现欠压或过压,势必影响HAPF的正常工作。再加上储能单元的多数闲置状态等原因,考虑有源滤波器在应用于风电场时,将其直流侧电容与储能装置进行并联,由于并联后的输出为直流电,所以并联后的直流侧电容与储能装置可等效为直流电源,不用再进行直流侧电压的控制,电容器安全性大大增加,且容量也可以适当减小,同时增加了储能单元的利用率。图1给出了风电场HAPF总体框图,图中左半部分为风电场的简化图,中间为无源滤波器,右边虚线内为有源电力滤波器的控制原理,包括信号采样、指令电流的生成和控制以及驱动与保护等部分。
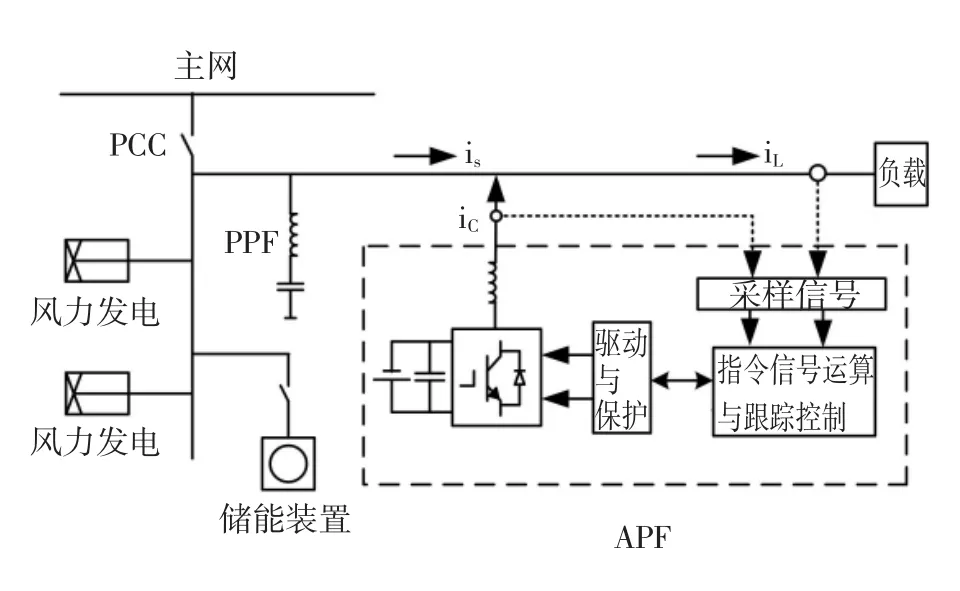
图1 风电场HAPF总体框图Fig.1 Overall diagram of HAPF in wind farm
2 后向线性谐波电流预测与分析方法
2.1 后向最小预测误差
若风电场谐波电流信号x(t)在t=0,1,2,…,k-1,k-m,k时刻的采样值分别为 x(0),x(1),x(2),…,x(k-1),x(k- m),x(k),由已知其中的x(k-m+1),…,x(k)等值来预测 x(k-m)值,则其线性预测值为
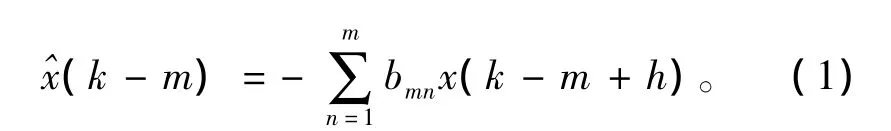
式中,bmn为后向线性预测系数,1≤h≤m。相应的线性预测误差为
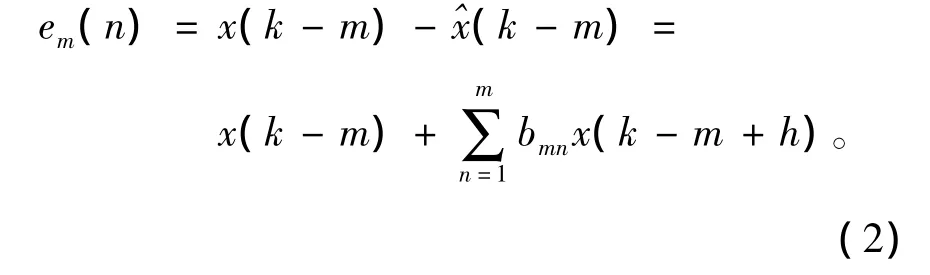
后向线性预测滤波器工作原理如图2所示。
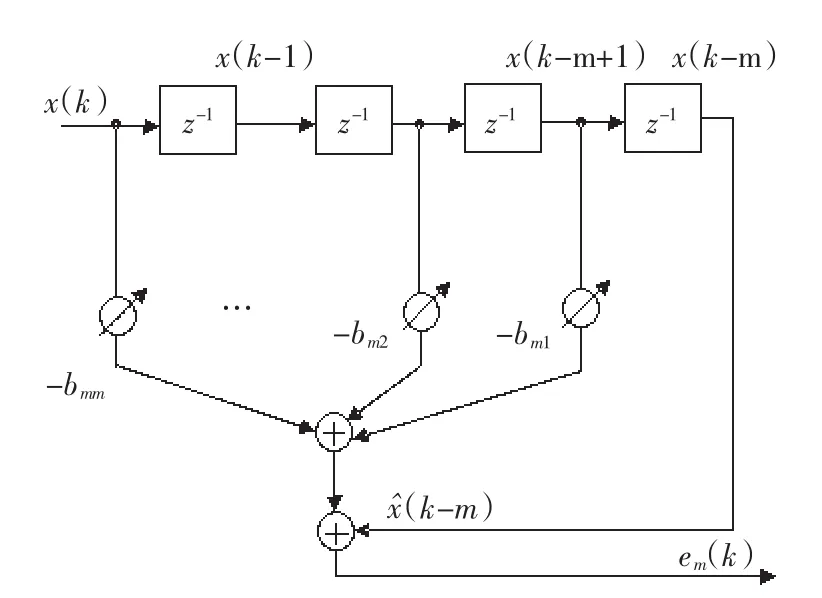
图2 后向线性预测滤波器Fig.2 Backward Linear Prediction Filter
使线性预测误差最小的bmn称为最佳预测系数,为求其误差最小值,令其对bmn的偏导数为零,可得
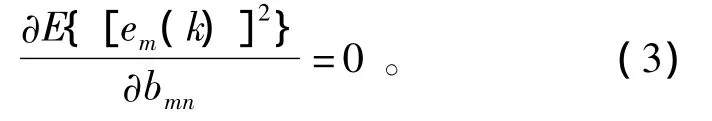
从而得到后向线性预测的正交方程为
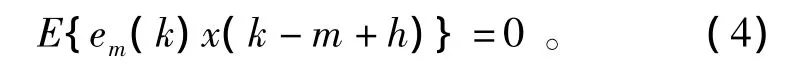
由式(1)、(4)可得bmn必须满足的正则方程为
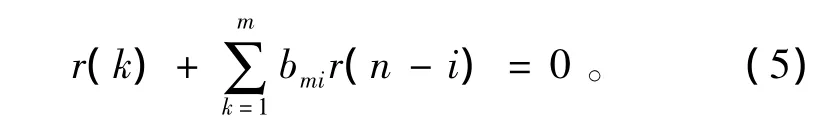
式(5)中 r(k)=E{x(n)x(n-h)},由式(4)、式(5)得最小后向预测误差方程为
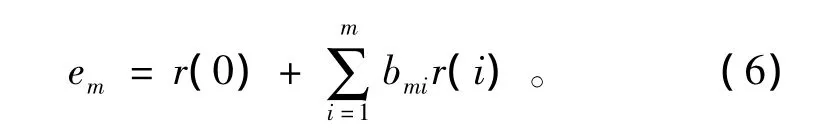
定义后向预测误差em(n)与前向预测误差e'm(n)的相关系数为
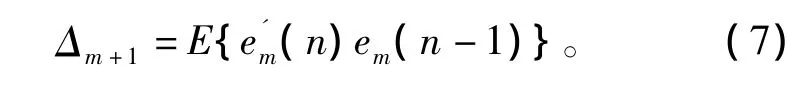
对于最佳预测系数,根据式(4)及前向线性预测方法[4]可得
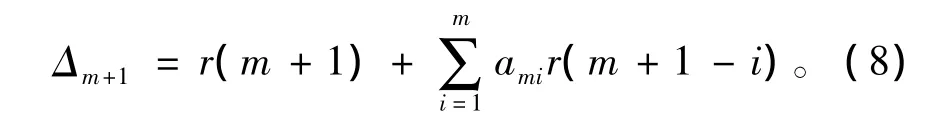
由Levinson-Durbin算法可得最小预测误差及系数的阶更新方程为
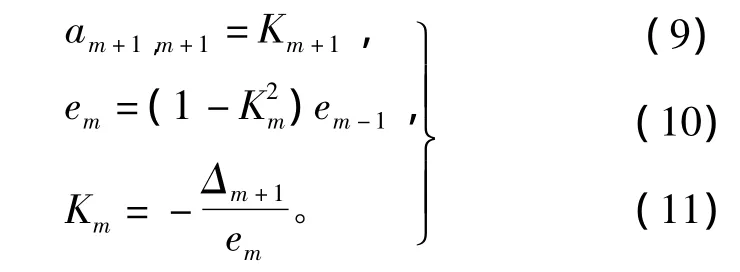
式中,的Km称为反射系数,在线性预测中起着比较重要作用。
2.2 后向谐波电流预测方法
风电场HAPF后向谐波电流预测方法如图3所示,主要由谐波电流检测、预测、控制与补偿模块组成。检测模块采用傅里叶算法,计算出t时刻风电场谐波电流,并送入预测模块。预测模块采用后向谐波电流预测方法,根据t时刻负载的谐波电流和历史经验数据,计算出t-1时刻的谐波电流。然后从负载过去的谐波电流数据中等间隔地抽取ih(km+1),ih(k-m+2),…,ih(k-m+9)等值,建立后向线性预测模型,根据这些历史数据,采用该方法预测出ih(k-m)值;再由 ih(k-m),ih(k-m+1),…,ih(k-m+8)等值,类似预测出ih(k-m-1)值;同理可得ih(k-m-2)、ih(k-m-3)…值。对这些预测值进行分析和综合,为近期谐波电流的评估及制定后一段时间谐波电流控制方法提供可靠依据。
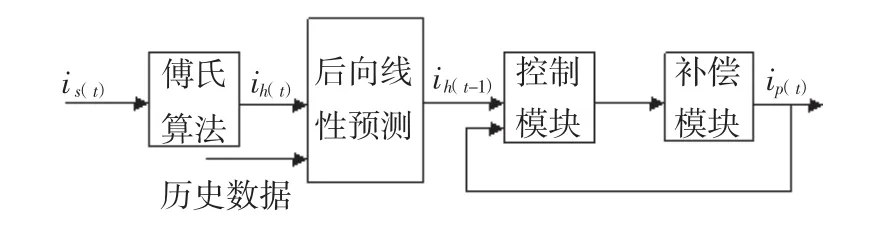
图3 后向谐波电流预测方法Fig.3 Backward harmonic currents prediction method
控制模块采用显式预测控制方法,该方法基于动态规划思想,利用多参数二次规则技术(multipara-metric quadratic programming,MP-QP)设计控制器,并给出保证闭环系统稳定性的局部固定状态反馈增益。考虑到预测控制的滚动优化原理,只存储k=0时单级优化问题最优控制律的相关信息。这样,不仅有效减小离线求解优化问题的复杂度而且节约控制律所需的存储空间。该方法使得在线操作只需查找当前状态所在的分区并计算相应的最优控制律,相对于传统预测控制方法,不仅能够保证系统的稳定性,还可大大减小最优控制律的在线计算时间。
3 仿真与实验
3.1 仿真
为了检验本文所提谐波电流预测方法的有效性,采用Matlab软件对其进行了仿真。主要参数为:交流侧串联等效阻抗为0.02 Ω,并联等效阻抗为460 Ω,电抗器电感值为1.8 mH,储能单元等效内阻为0.2 Ω,直流侧电容为3 000 μF,储能单元输出电压为550 V,三角载波频率为3 000 Hz。
1)风电场风力突变情况
模仿风电场风力突变情况,在0.25 s时刻,使得谐波电流的幅值突变为原来的2倍,在0.3 s时刻突变回原来值。此时,灰色预测方法和后向线性预测方法的预测与实际电流波形如图4所示。对比图4中两个波形可以得知,图4(a)的整个过程中预测值与实际值有一定的偏差,图4(b)中除了在两个突变瞬间谐波预测值稍微滞后于实际值,但很快预测值跟踪上了实际值,其他时间预测值和实际谐波电流值十分吻合。由此可见后向线性预测方法具有较好的动态响应特性和精确度。
2)风电场中三相负载电流幅度突变情况
图5(a)为补偿前三相负载电流波形,在0.25 s及0.3 s时三相负载电流幅度发生突变现象,图5(b)、(c)为灰色预测方法和后向预测方法补偿后负载电流波形。由图可见,利用后向预测方法的三相电流幅度波动的状况得到了明显改善,表现出良好的对电流幅度突变的平衡及稳定效果,比灰色预测方法应对突变的能力要强。
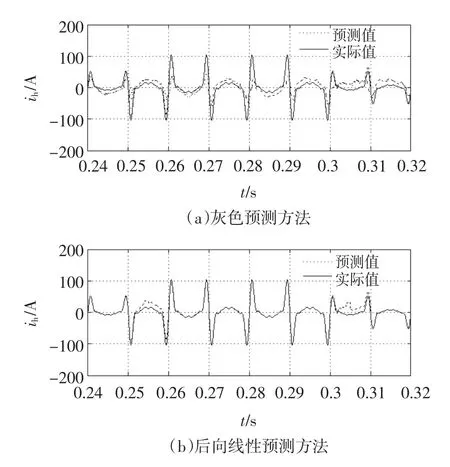
图4 两种方法的预测和实际谐波电流波形Fig.4 Predict and practical harmonic currents of two method
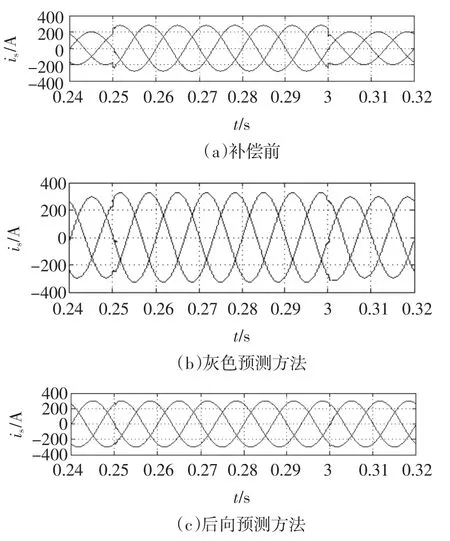
图5 两种方法的HAPF三相电流幅度突变补偿效果Fig.5 Three-phase current amplitude mutation compensation waveform of two method
3)风电场中谐波电流治理情况
图6(a)为补偿前网侧电流波形,畸变严重,对比图6(b)、(c)中的电流波形,采用灰色预测方法后电流畸变率为3.31%,而采用后向预测方法后电流畸变率仅为1.32%,波形十分接近正弦波,输出电流波形效果比灰色预测方法要好的多。
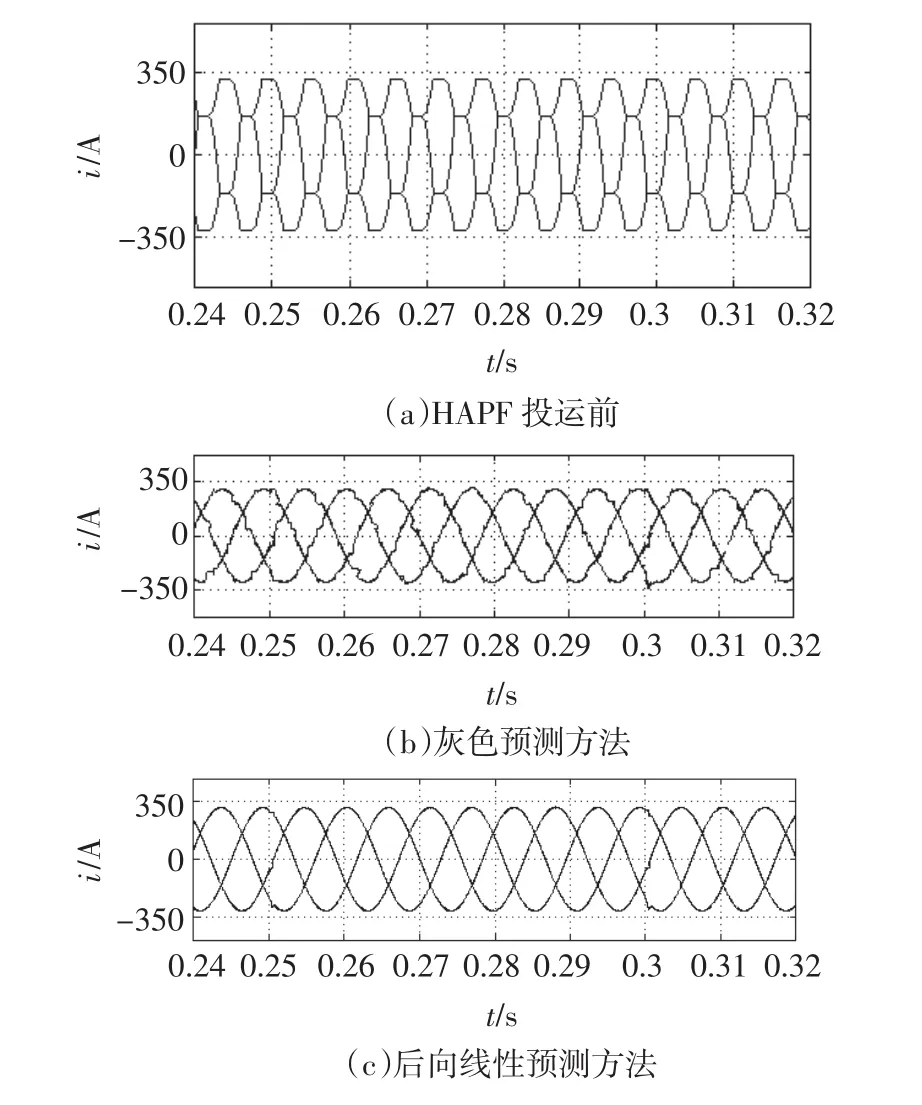
图6 网侧电流波形Fig.6 Waveforms of system currents
3.2 实验
实验用的元器件参数为:Fluke F435型号谐波测试仪;APF的容量为0.5 kVA;开关频率为5 kHz;直流电容器容量为1 100 μF;直流电压为300 V;PPF的参数见表1。分别对风电场中的感应电动机、电力电容器及工业整流负载谐波源进行了实验。
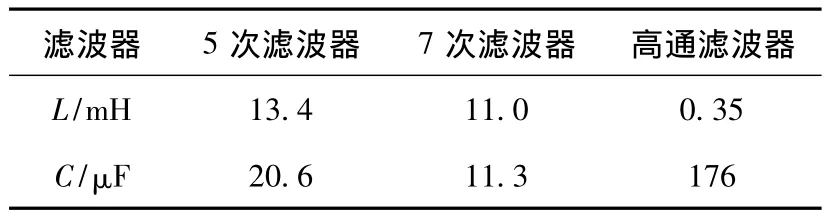
表1 系统PPF参数Table 1 System PPF parameter
1)风电场中感应电动机负载情况
采用上述型号谐波测试仪对某风电场中电动机负载各次谐波电流的测试值和本文方法预测出的各次谐波电流值如表2所示。表中还给出了各次谐波的预测误差(定义为测试值与预测值的差值和测试值之比),其中最高、最低误差分别为1.42%、0.16%。表明该方法对感性负载具有较高的精度。
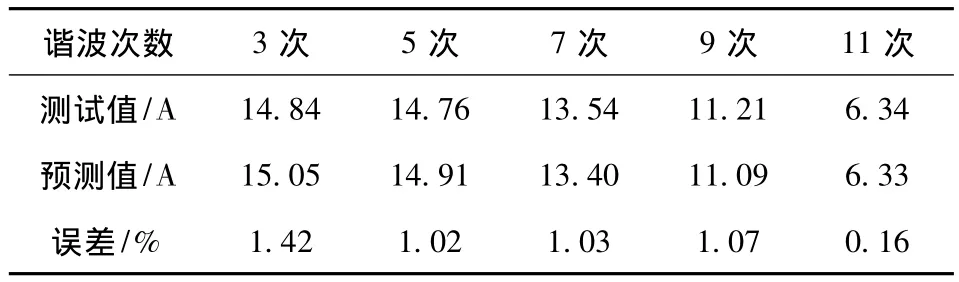
表2 电动机负载各次谐波电流Table 2 Each harmonic current of motor load
2)风电场中电力电容器负载情况
采用上述方法对风电场中电力电容器负载谐波源进行了实验,测出及预测出的各次谐波值如表3所示。最高误差为1.54%,最低误差为0.52%,证明了该方法针对容性负载同样具有较高的精度。
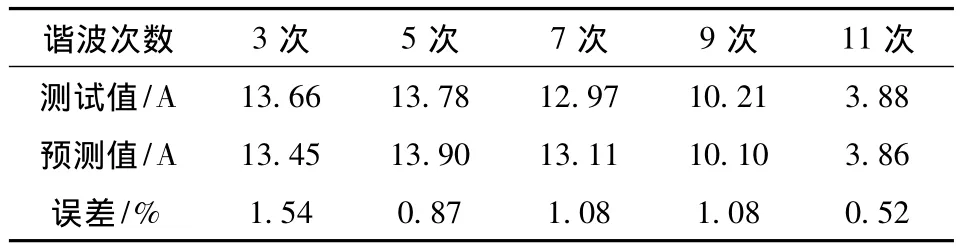
表3 电力电容器负载各次谐波电流Table 3 Each harmonic current of power capacitor load
3)风电场中感应工业整流负载情况
对某风电场工业用6脉波整流负载产生的谐波情况进行了预测实验,预测与实测谐波电流对比情况如表4所示。由表中数据对比可以看出,最高误差为1.30%,最低误差为0.34%,再次证明该方法工业实际应用的可行性及可靠性。
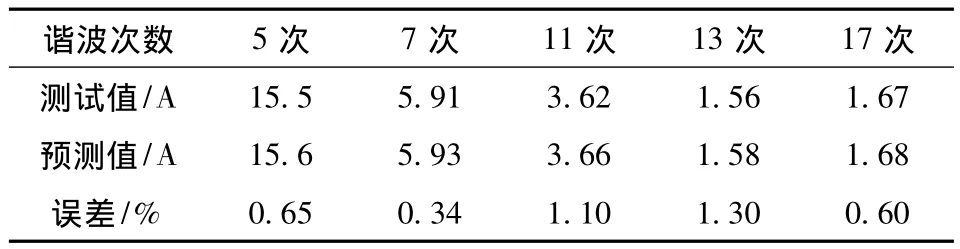
表4 整流负载各次谐波电流Table 4 Each harmonic current of rectifier load
4)综合补偿效果
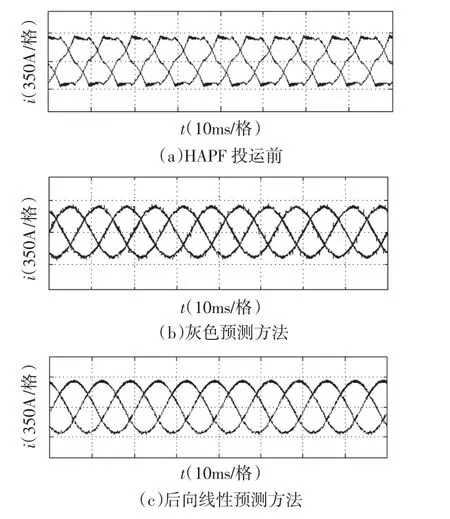
图7 两种方法补偿后负载电流波形Fig.7 Waveforms of system currents after compensate of two method
HAPF补偿风电场某负载电流波形如图7(a)所示,谐波含量高,波形严重畸变。采用灰色预测方法和后向线性预测方法的补偿效果如图7(b)、(c)所示,对比图7中的3个电流波形可知,基于后向线性预测方法HAPF的波形十分接近正弦波,输出电流波形效果比传统灰色预测方法电流畸变率要小,波形质量更好。
4 结论
该文提出的HAPF后向线性谐波电流预测方法能对风电场负载谐波电流进行准确预测和最小误差补偿,具有以下特点:
1)该方法适用于突发性、随机性强的风电场谐波电流补偿情况,对风力突变、三相负载电流幅度突变等情况均有良好的补偿效果。
2)对于风电场感性、容性等负载各次谐波的最小预测误差仅有0.16%。
3)对风电场负载谐波电流综合补偿效果好,电流畸变率仅有1.32%。
[1]杨向真,苏建徽,丁明,等.面向多逆变器的微电网电压控制策略[J].中国电机工程学报,2012,32(7):7 -14.YANG Xiangzhen,SU Jianhui,DING Ming,et al.Voltage control strategies for microgrid with multiple inverters[J].Proceedings of the CSEE,2012,32(7):7 -14.
[2]王成福,梁军,孙宏斌,等.风电场混合无功功率补偿系统及其控制策略研究[J].电机与控制学报,2013,17(5):38 -44.WANG Chengfu,LIANG Jun,SUN Hongbin,et al.Hybrid reactive power compensation system and its control strategy for wind farm[J].Electric Machines and Control,2013,17(5):38 -44.
[3]曾正,赵荣祥,杨欢.含逆变器的微电网动态相量模型[J].中国电机工程学报,2012,32(10):65 -71.ZENG Zheng,ZHAO Rongxiang,YANG Huan.Dynamic phasors model of micro-grid with grid-connected inverters and simulation[J].Proceedings of the CSEE,2012,32(10):65 -71.
[4]李圣清,罗晓东,李永安,等.基于前向线性预测理论的混合电力滤波器谐波电流预测方法[J].中国电机工程学报,2011,31(34):100-104.LI Shengqing,LUO Xiaodong,LI Yongan,ZENG Lilin,HE Zhengping.A harmonic current forecasting method for hybrid active power filters based on the forward linear prediction theory[J].Proceedings of the CSEE,2011,31(34):100 -104.
[5]李圣清,张彬,栗伟周,等.含微网的配网统一电能质量调节装置[J].电机与控制学报,2014,18(6):90 -95.LI Sheng-qing,ZHANG Bin,LI Wei-zhou,et al.Unified power quality conditioner of distribution network containing micro-grid[J].Electri c Machines and Control,2014,18(6):90 -95.
[6]漆铭钧,罗安,刘定国,等.有源电力滤波器参考电流的预测方法及其实现[J].中国电机工程学报,2009,29(7):128 -134.QI Ming-jun,LUO An,LIU Ding-guo,et al,LI Feng.Prediction of the Reference Current of Active Power Filter and Its Realization[J].Proceedings of the CSEE,2009,29(7):128 -134.
[7]HAN B,BAE B,KIM H,et al.Combined operation of unified power quality conditioner with distributed generation[J].IEEE Transactions on Power Delivery,2006,21(1):330 -338.
[8]张彬,李圣清,徐天俊,等.一种新型的太阳能逆变器并网控制方案[J].湖南工业大学学报,2014,28(3):52 -55.ZHANG Bin,Li Shengqing,Xu Tianjun,et al.A new grid-connected control scheme of solar inverter[J].Journal of Hunan University of Technology,2014,28(3):52 -55.
[9]CUTRI R,MATAKAS L J.A new instantaneous method for harmonics,positive and negative sequence detection for compensation of distorted currents with static converters using pulse width modulation[C]//International Conference on Harmonics and Quality of Power.New York:IEEE Press,2005:33 -36.
[10]MOHAMED Y R,El-Saadany E F.Robust high bandwidth discrete-time predictive current control with predictive internal model:a unified approach for voltage-source PWM converters[J].IEEE Trans.on Power Electronics,2008,23(1):126 -136.
[11]MASTROMAURO R A,LISERRE M,KEREKES T,et al.A singlephase voltage controlled grid-connected photovoltaic system with power quality conditioner functionality[J].IEEE Trans.on Industrial Electronics,2009,56(11):4436 -4444.
[12]CHENG Zhongyuan,WU Bin.A novel switching sequence design for five-level NPC/H-bridge inverters with improved output voltage spectrum and minimized device switching frequency[J].IEEE Transactions on Power Electronics,2007,22(6):2138-2145.
[13]栗伟周,李圣清,徐文祥,等.一种实用型电能质量调节装置及其控制[J].湖南工业大学学报,2013,27(5):53 -71.LI Weizhou,LI Shengqing,XU Wenxiang,et al.Design and Control of Practical Power Quality Conditioner[J].Journal of Hunan University of Technology,2013,27(5):53 -71.
[14]唐鑫鑫,惠晶.基于模型算法预测控制策略的APF的研究[J].电力电子技术,2011,45(11):92 -111.TANG Xinxin,HUI Jing.Research on predictive control of APF based on model algorithmic control[J].Power Electronics,2011,45(11):92-111.
[15]徐子利,罗春风.基于灰色预测理论的并联型混合电力有源滤波器研究[J].电力系统保护与控制,2009,37(22):83-86.XU Zili,LUO Chunfeng.Study of hybrid filter connected in series APF with PF based on grey prediction control[J].Power System Protection and Control,2009,37(22):83 -86.
[16]颜文旭,韩立圣,惠晶,等.三相四线有源电力滤波器新型神经预测控制[J].电力系统及其自动化学报,2011,23(1):28-33.YAN Wenxu,HAN Lisheng,HUI Jing,et al.Novel neural network predictive control scheme for three-phase four-wire active power filter[J].Proceedings of the CSU-EPSA,2011,23(1):28-33.

