一种三维磁路永磁电机的集中参数磁路模型

张继鹏， 陈鹏， 苏锦智， 孙立志

(1.包头市永磁电机研究所，内蒙古包头014030;2.哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

0 引言

许多电机的磁路结构是三维的，往往是由径向磁路和轴向磁路共同构成的。常见的电机类型包括传统的爪极电机、混合步进电机、基于横向磁场原理的旋转电机、以及一些新出现的永磁电机及开关磁链运行原理电机等等。这些电机往往具有较单一径向磁场或轴向磁场电机更高的功率密度，适合于一些多极低速应用领域如直驱风力发电机等［1－4］。

对于这些具有三维磁路结构的电机分析，传统的二维电磁场有限元分析无法准确描述电机的电磁性能，需要进行三维电磁场有限元计算。而三维数值计算方法的计算量巨大，计算时间长，不利于电机的参数计算和结构优化。而采用磁路计算方法，如果能够在十分接近磁场数值计算方法结果的情况下，将大大简化计算量，提高电机设计、分析和优化的效率。其中集中参数磁路模型的研究方法具有计算准确的特点，尤其可以简化三维磁路结构电机的分析和设计优化工作。

对于集中参数磁路模型研究方法，文献［5－9］建立了二维磁路结构的永磁开关磁链电机的集中参数磁路模型并进行了磁路解析计算，取得了与磁场计算相近的结果。文献［5］提出了采用三维集中参数磁路模型分析单相永磁开关磁链电机，计算了气隙磁场分布，电机反电动势及电感波形，平均静态转矩，同时分析了定子外径漏磁和端部漏磁对反电动势波形的影响，以及电机轴向长度和永磁体尺寸对端部效应的影响。文献［6］建立了永磁开关磁链电机的集中参数磁路模型，并分别采用磁路解析方法及磁场有限元计算方法分析了不同定转子极数时的电机参数以及电磁转矩。文献［7］针对电机边缘区域及局部区域的饱和效应，建立了非线性等效磁路模型来分析电机静态参数，并将解析计算结果与磁场有限元计算结果相比较。文献［8］分析了永磁体磁动势与电枢反应磁动势的交叉耦合效应和电机饱和效应，分别建立了以永磁体磁动势为磁动势源和以电枢反应磁动势为磁动势源的双集中参数非线性磁路模型。文献［9］建立了单相永磁开关磁链电机的3维集中参数磁路模型，并分析研究了电机轴向长度及永磁体尺寸对电机端部效应的影响，并用3D有限元计算对磁路计算的结果进行了验证。

本文针对一种类爪极电机结构，在对空载静磁场及电枢反应磁场计算、分析的基础上，根据电机各部分在不同定、转子相对位置时的磁场分布情况，对三维磁路结构进行集中参数磁路模型建模，并推导出节点磁动势矩阵，通过对矩阵进行解析计算以及对计算结果的分析，推导出电机各主要电磁参数的解析表达式。该三维磁路结构集中参数磁路模型解析表达的建立，对其他三维磁路结构电机的计算和分析工作具有普遍参考意义。

1 三维磁路永磁电机的磁场分析

1.1 电机结构及运行原理

图1为所研究的三维磁路电机结构图。电机采用外转子结构，定子采用类爪极磁极形状及环形集中绕组，有利于大功率化时的绕组制造及绕组绝缘，相较爪极电机又可以减少极间漏磁;转子采用软磁材料，转子轭上安装着2P个永磁磁极，磁钢的充磁方向为外转子切线方向。定子铁心分为3段，中间段为轴向磁路，外径较小，其外周缠绕一相集中绕组，为环形线圈;两侧铁心为径向磁路，两铁心结构相同且相互错开180°电角度，外径为电枢直径，其上面开有P个齿(槽)，槽内不放置绕组，与外转子共同形成气隙。

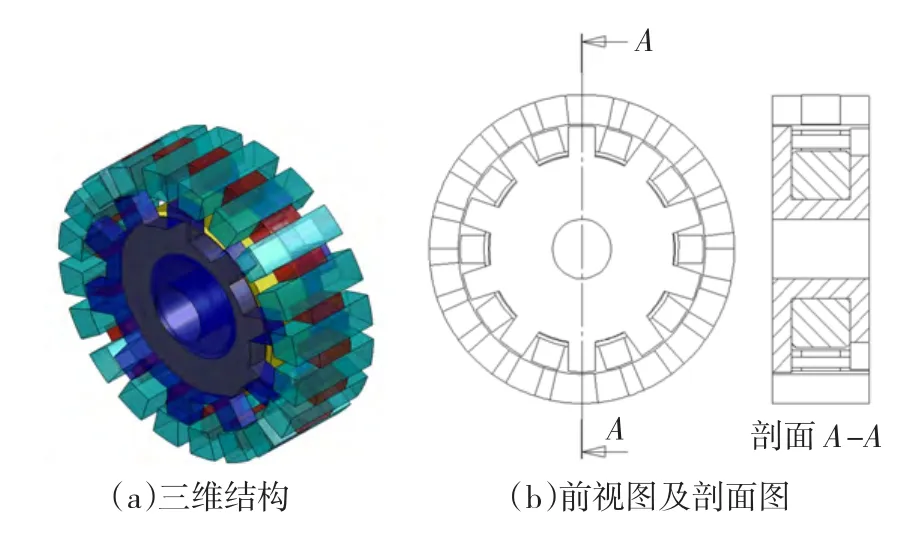
图1 所研究电机结构Fig.1 Machine structure

该电机的主磁通路径如图2所示，当转子旋转到图2(a)位置时，永磁体产生的主磁通沿切线方向进入转子铁心，磁场方向变为径向，然后主磁通经径向气隙进入一侧定子铁心的齿部，再通过中间轴向铁心，进入另一侧定子铁心，并通过另一侧定子铁心的齿部重回气隙，经转子铁心及永磁体闭合形成三维磁路，这时定子集中绕组内磁链方向沿轴线方向，即为磁链开状态;当电机转子旋转到图2(b)所示位置时，永磁体产生的主磁通经过转子铁心构成的主磁极及气隙，在一侧定子铁心的齿部内直接闭合，此时集中绕组不匝链磁通，即为磁链关状态。转子的持续旋转，主磁通将切换其路径，不断进行磁链开、关状态的转换，从而使定子集中绕组中匝链的磁通的大小和方向均发生变化，进而感应出反电动势。因此该电机结构也可以称为开关磁链永磁电机。

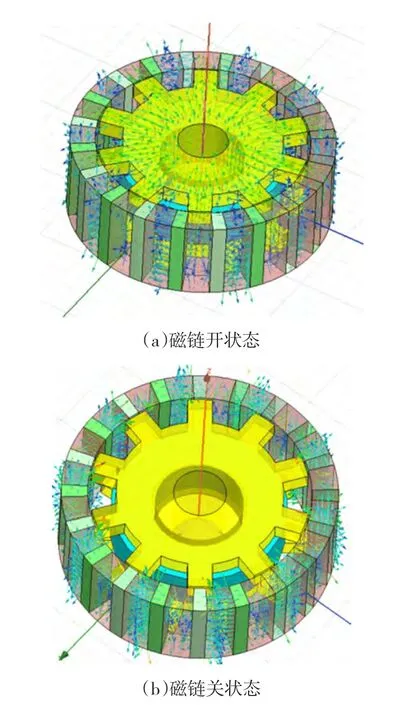
图2 磁链开、关状态磁密分布Fig.2 Flux density of the PMSM

上述结构为单相结构，在单相电机的基础上可以进行多相化，所以单相电机的分析具有代表性。所计算电机参数如表1所示。

表1 所计算电机的设计参数Table 1 Parameters of the motor

1.2 磁链开状态主磁通分布

磁链开通时，侧部定子铁心、中间铁心、转子主磁极磁密分布如图2所示，两侧定子铁心轭部中轴向磁场向径向磁场逐步过渡，齿部中为径向磁场，且齿部磁密大于轭部磁密;定子中间铁心中大致为均匀的轴向磁场，两端磁密稍高于中部磁密，且两侧边缘靠近侧部铁心处磁密含有径向分量;由于特殊的三维磁路结构，转子极靴可分为前、中、后3部分，从极靴A第一部分经过第二部分进入转子磁钢，再进入极靴B第二部分经过第三部分进入另一侧定子齿，从磁密分布的层次也可清楚看到。由磁密分布可知极靴A第三部分和极靴B第一部分存在漏磁，磁密较低，同时由于中间段靠近磁钢，故磁密也较低。

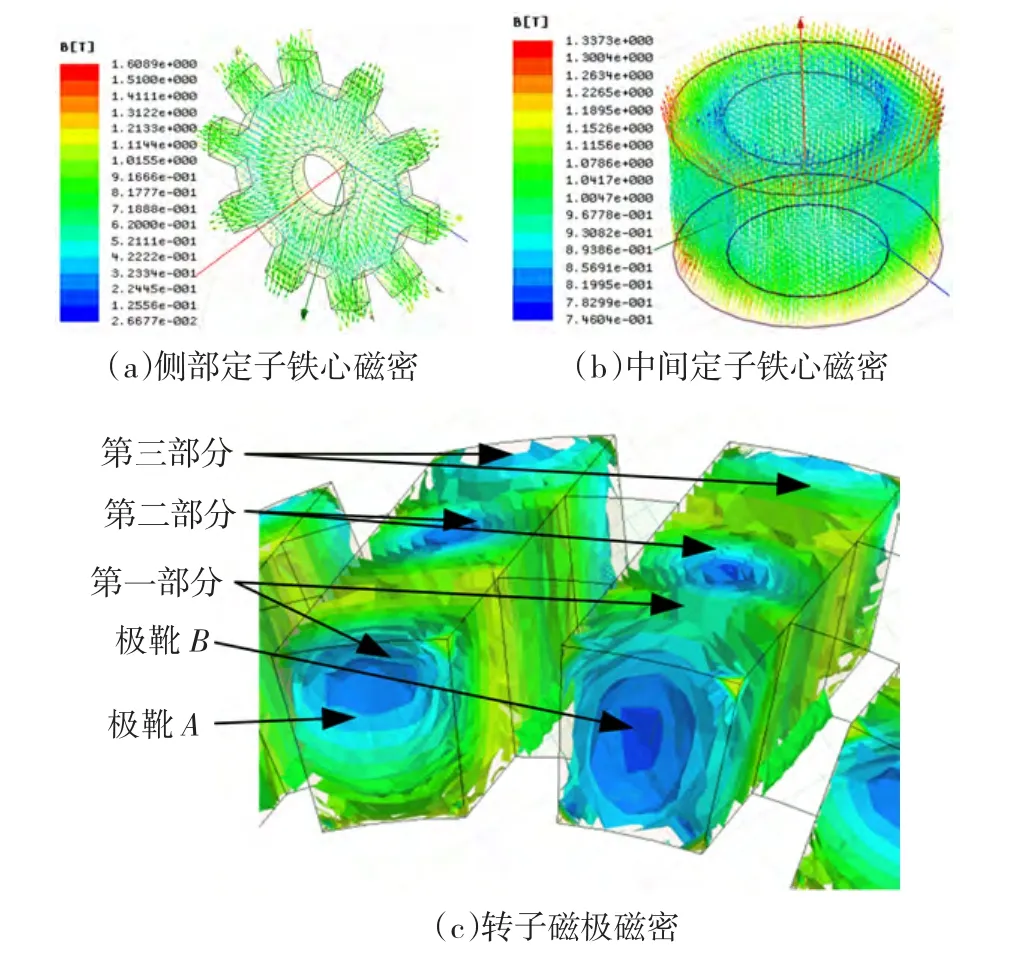
图3 磁链开状态主磁场分布Fig.3 The main magnetic field distribution at flux-on state

1.3 磁链开状态漏磁场分布

电机槽漏磁无法通过转子磁钢闭合，因此空载漏磁场主要集中在气隙及其附近的定子齿和转子极靴中。漏磁场主要分为以下5个部分。

1)漏磁场从转子极靴经气隙进入定子齿，再经气隙返回相邻转子极靴，如图4(a)所示。

2)由于磁钢轴向长度小于极靴轴向长度，两相邻极靴之间会存在漏磁场。漏磁路径由两相邻极靴及它们之间的气隙和磁钢组成，如图4(b)所示。

3)轴向端部漏磁如图4(c)所示，漏磁路径从极靴出发，经转子端部空气、相邻极靴和磁钢闭合。

4)由于采用混合式磁极结构，转子圆周外侧含有如图4(d)所示的平行于径向分布的漏磁场。

5)漏磁路径从极靴出发，沿径向方向进入定子两侧部铁心之间气隙，沿轴向方向进入定子齿内侧，最后经气隙返回极靴，如图4(e)所示。

这5部分空载漏磁场中，第1、2部分为主要组成部分，而第3、4、5部分所占比重不大;第1、4部分属于二维路结构，第2、3、5部分属于三维磁路机构;第1、5部分通过定、转子闭合，漏磁通大小随定转子相对位置变化而变化明显;第2、3、4部分直接在转子闭合，漏磁通大小不受定转子相对位置变化影响，而受电机转子尺寸影响较大。

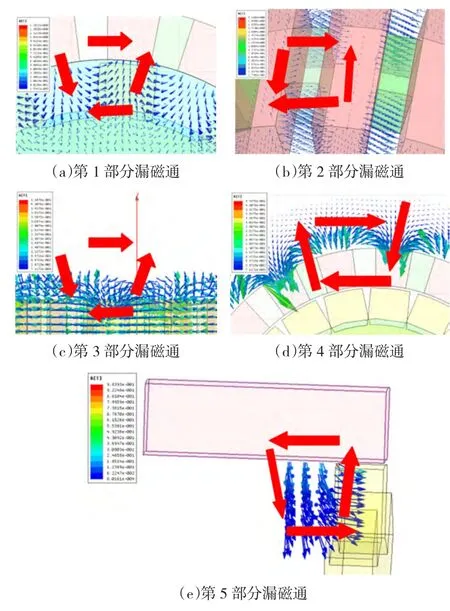
图4 5种漏磁通分布Fig.4 Five pathes of leakage flux distribution

1.4 磁链关状态磁场分布

磁链直接闭合时的气隙空载磁链分布如图5所示，由于定子齿正对磁钢，主磁通由极靴进入气隙后分别沿径向和周向两种路径进入定子齿，再从齿部另一侧经相似路径回到极靴。

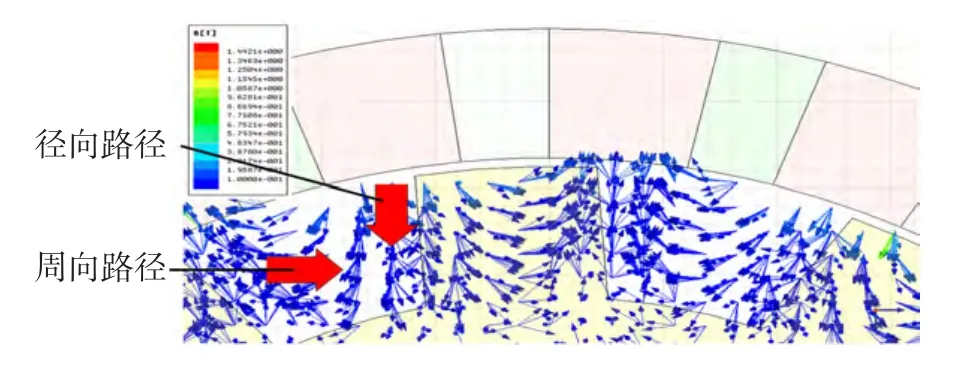
图5 转子极靴磁密分布Fig.5 The magnetic flux density distribution in rotor poles

磁链关闭情况也存在5个部分漏磁场，第1、5部分随定转子相对位置变化明显，在磁链关闭时漏磁通明显降低。第2、3、4部分不受定转子相对位置影响，因此漏磁通基本不变。

2 电机磁路模型

2.1 磁路元素模型的建立

基于节点磁动势矩阵的集中参数磁路模型的基本原则如式(1)所示。

其中Φ、F、P分别代表一个磁路元素的磁通、磁动势和磁导。磁路元素是指在磁路模型中对电机结构的某一部分(例如定子齿部、定子轭部、气隙等)进行的磁路模型化等效，例如定子齿可等效为一长方体磁路元素，长方体磁导如式(2)所示。

其中:μr、μ0分别代表相对磁导率和真空中的磁导率;Lr、Sr分别为元素的有效长度和横截面积。

永磁体等效磁通Φm=BrSm，Sm、Br分别为永磁体垂直于充磁方向的横截面积和剩磁，永磁体的磁导可由式(2)推出。

各部分的磁导可由各部分磁密及磁化特性求得，磁密Bps由式(3)所示。

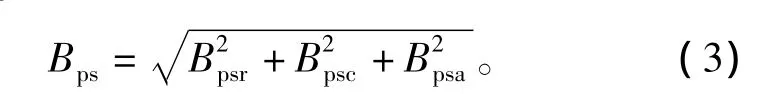
其中 Bpsr、Bpsc、Bpsa分别为径向、圆周方向及轴向磁密。最后极靴等效合成磁导Pps由式(4)所示，其他非线性区域的磁导推导与此推导过程相同。

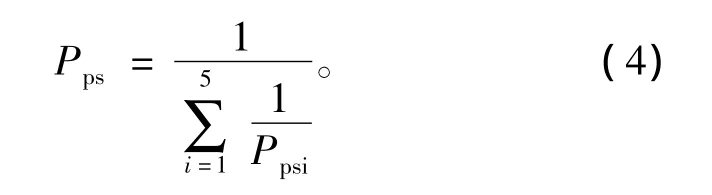
当电机定、转子极数较多时，可在直角坐标系中建立磁路解析模型［8］，图6给出了两种典型定、转子相对位置时气隙磁通分布。

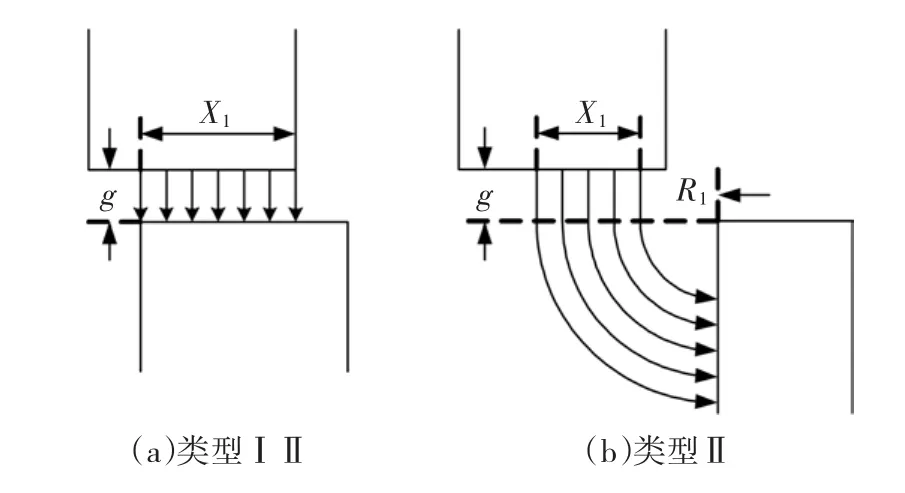
图6 两种典型定、转子相对位置时气隙磁通分布Fig.6 Two typical air gap flux distribution diagrams

相应的气隙磁导如式(5)～式(8)所示。

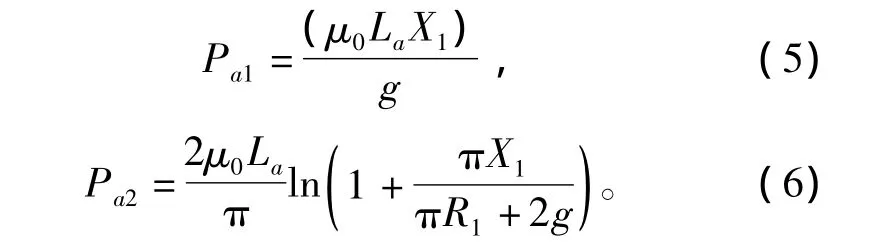
其中μ0、La分别为真空中磁导率和气隙轴向长度。

两相邻转子极靴径向外表面及轴向外表面的理想磁通路径如图7所示，由半圆柱体磁通路径和半圆环磁通路径构成，相应的磁导如式(7)、式(8)所示。

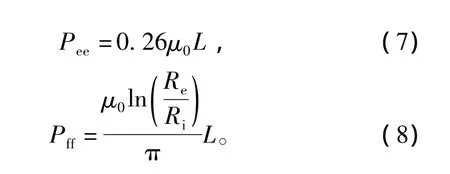
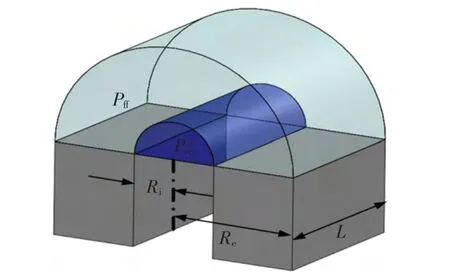
图7 电机轴向与径向端面理想磁通路径Fig.7 The ideal flux path of motor axial and radial face

当电机旋转至图8所示位置，定子齿正对转子极靴，电机为磁链开状态同时绕组磁链达到最大值，箭头表示主磁通及漏磁通路径。气隙主磁通仅由正对主磁极提供，这将大大简化磁路模型复杂程度，进而提高磁路计算准确性。

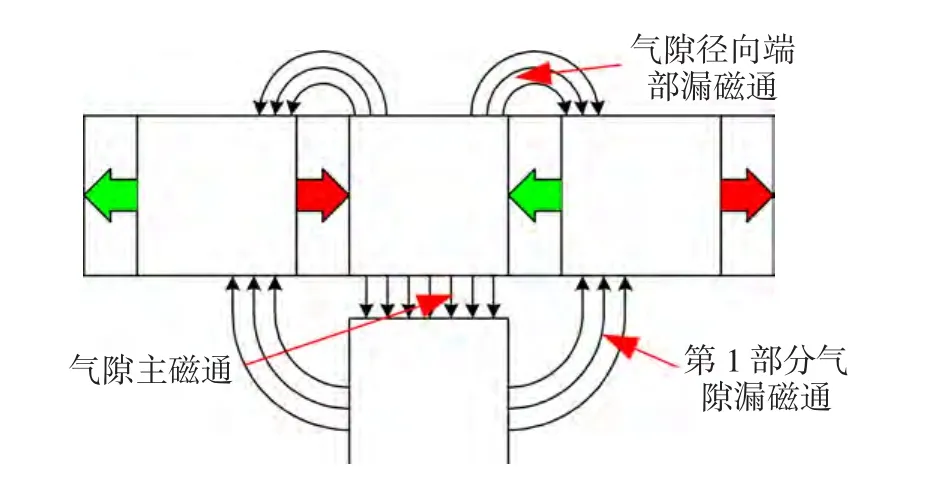
图8 气隙主磁通及漏磁通路径Fig.8 The path of air gap flux and leakage flux

电机旋转至图9所示位置时，仍为磁链开状态，这时气隙主磁通逐渐减小而气隙漏磁通逐渐增加同时绕组磁通匝链逐渐减小。

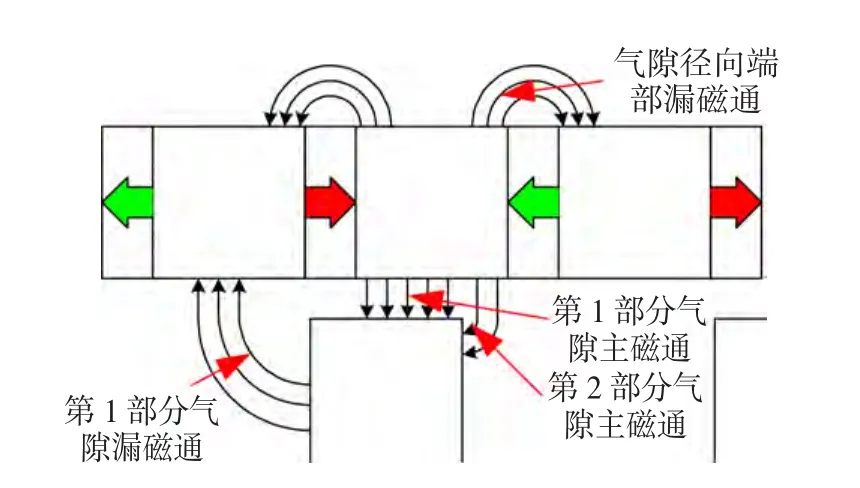
图9 气隙主磁通及漏磁通路径Fig.9 The path of air gap flux and leakage flux

电机旋转至图10所示位置时，仍为磁链开状态，与图9主要区别在于漏磁通路径增加了径向路径。

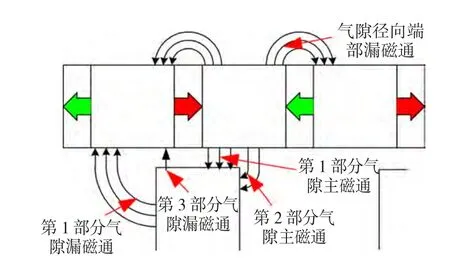
图10 气隙主磁通及漏磁通路径Fig.10 The path of air gap flux and leakage flux

电机旋转至图11所示位置时，定子齿正对转子磁钢，气隙主磁通与气隙漏磁通相等，相当于主磁通在定子齿部直接闭合，电机处于磁链关状态。

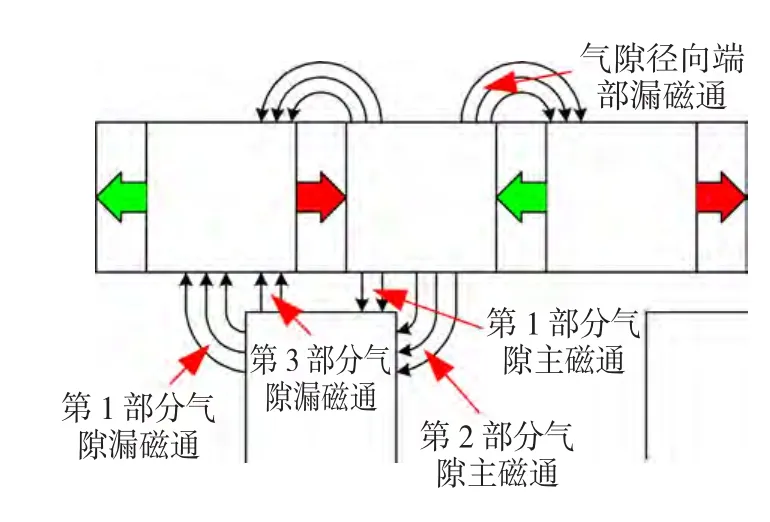
图11 气隙主磁通及漏磁通路径Fig.11 The path of air gap flux and leakage flux

2.2 集中参数磁路模型的建立

为建立表1中电机集中参数磁路模型，需要简化分析，并作如下假设。

1)电机极数较多，可对定子齿、转子磁钢和转子极靴等部分近似成长方体磁路元素;

2)磁钢轴向长度与极靴轴向长度相等，避免计算空间分布较为复杂的第2部分漏磁场;

3)两相邻转子极靴径向及轴向端部漏磁通路径与漏磁导表达式相同，可合到一处;

4)转子极靴同时为一侧定子齿提供主磁通以及为另一侧定子齿提供漏磁路径，可将沿轴向分成两部分，前侧极靴和后侧极靴。

下面针对磁链开状态所建立的集中参数磁路模型。磁路模型中，Φm为单个永磁体提供的总磁通;Pm为永磁体的内磁导;Prf1为主磁通转子前侧极靴的磁导;Prf2为漏磁通转子前侧极靴磁导;Prb1为主磁通转子后侧极靴磁导;Prb2为漏磁通转子后侧极靴磁导;Pst为定子齿部磁导;Psy为定子轭部磁导;Psm为定子中间铁心轭部磁导;Pa1及Pa2为图7气隙主磁导和气隙漏磁导;Pa3为转子极靴径向及轴向端部气隙漏磁导。由于每个主磁极相对独立工作且每个磁钢和极靴的尺寸均相等，以及电机结构的对称性，因此每对主磁极对应的 Φm、Pm、Prf1、Prf2、Prb1、Prb2、Pst、Psy、Pa1、Pa2、Pa3等参数对称关系。这将大大简化磁动势矩阵的计算。

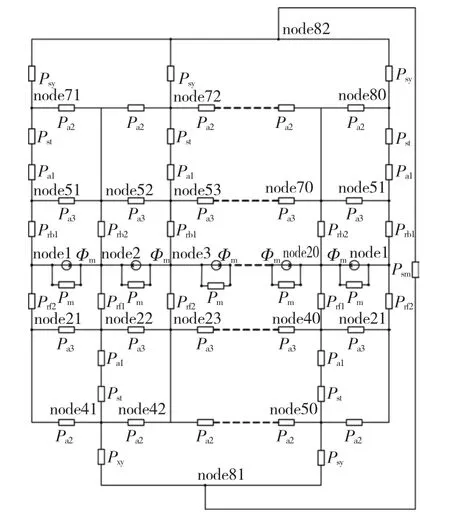
图12 集中参数磁路模型Fig.12 The lumped parameter magnetic circuit model

2.3 磁动势方程建立及简化

根据上述集中参数磁路模型可以建立磁动势方程，得到全部节点的磁动势进而求得相应的电机参数。磁动势方程的矩阵形式如式(9)所示。

其中:F是待求节点磁动势向量;Φ为已知磁通源向量;P为磁导矩阵。电机转子Nr个极，定子Ns个极且Nr=Ns=N，F、Φ、P如式(10)～式(12)所示。

当极数N=20时，需解82个方程及6 724个磁导，因此需要对磁导矩阵简化。根据假设4将转子极靴分成前侧极靴和后侧极靴，且两侧极靴独立的与两侧部定子铁心组成闭合磁路，由于两个闭合回路磁通路径相同，方向相反，由对称性可知Prf1=Prb2=Pr1、Prb1=Prf2=Pr2。根据节点磁动势对称相等的关系，通过利用元素磁导对称性，无论定转子极数多少，都可简化成10种节点磁动势。

2.4 计算结果

将电机各部分磁导值代入到式(10)～式(12)中，计算出各节点的磁动势，根据式(1)即可得出各支路磁通，根据电机结构的对称性，仅需计算出电机一次磁链开状态至下一次磁链关状态之间的1/4周期绕组主磁通，即可得到绕组整个周期匝链主磁通的分布情况。定义z轴正方向为绕组主磁通正方向，则主磁通Φ1如下式所示。

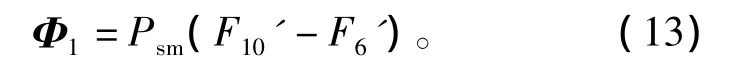
采用等效磁路方法及电磁场数值分析方法计算的绕组主磁通如图13所示。由于建立磁路模型时忽略一部分漏磁通及对电机各部分磁密的近似处理，采用磁路计算主磁通偏大，误差约为4%。

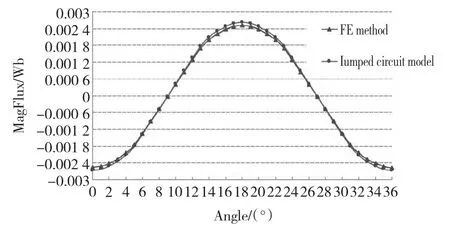
图13 磁路法及电磁场有限元法计算的绕组主磁通Fig.13 The winding main magnetic flux calculation of magnetic circuit method and finite element method

2.5 优化及分析

根据上述磁路计算模型计算方法，可以较为方便地对电机结构及参数进行优化。

定义定子凸极率为定子齿底圆弧半径同定子齿顶圆弧半径之比，用凸极率表征定子齿部高度变化对电机性能的影响。通过磁路参数模型进行计算，当定子凸极率为1.56时绕组内有效磁通最高，电机效率最佳。

采用等效磁路方法计算了定子齿宽变化时计算的绕组主磁通，当定子齿宽与定子齿距之比为0.5时绕组磁通最高，这与电磁场有限元计算方法的结论相吻合。

进一步进行计算分析，可以得到电机结构参数包括定、转子极数、电机整体轴向长度、定子齿部高度、定子齿宽、定子侧部铁心轴向长度、转子永磁体切向厚度、转子永磁体轴向长度等对电机性能的影响，进而可以选择最优值以实现电机理想的运行性能和工作特性。

样机目前正在制造过程中。

3 结论

三维磁路结构永磁电机往往具有较高的力能指标。在本文所研究的电机结构中，定子采用类爪极磁极形状及环形集中绕组，有利于大功率化时的绕组制造及绕组绝缘，相较爪极电机又可以减少极间漏磁;转子上采用混合磁极以降低永磁材料损耗。针对三维有限元磁场计算复杂，计算周期长，不利于电机参数设计优化，在磁场计算的基础上建立单相电机磁路模型，得到以下结论:

1)此三维磁路结构电机每对主磁极相对独立工作，并且每对主磁极磁链开关状态一致，共同提供气隙主磁场，参与能量转换。

2)由于电机工作的周期性，可对电机绕组磁链开关一次之间的1/4周期的磁路变化模型进行分析，降低模型复杂度。

3)电机结构的对称性，每一磁极对应的主磁通及漏磁场一致，对于任何极数的电机，均可将磁路模型中磁动势化简为一个10种节点的方程，具有普遍的适用意义。

由于节省大量计算量，因此可采用集中参数磁路模型计算的方法分析多个电机参数同时变化时对电机性能的影响，节约了大量计算时间。

［1］CHEN Y C，PILLAY P，and KHAN A.PM wind generator topologies［J］.IEEE Transactions on Industry Applications，2005，41(6):1619－1626.

［2］WANG F X，BAI J L，HOU Q M，et al.Design features of low speed permanent magnet generator direct driven by wind turbine［C］//Proceedings of the Eighth International Conference on Electrical Machines and Systems(ICEMS)，Sept.2005，Nanjing.2005(2):1017－1020.

［3］POLINDER H，BANG D，VAN ROOJI，et al.10 MW wind turbine direct-drive generator design with pitch or active speed stall control［C］//IEEE International Electric Machines ＆ Drives Conference(IEMDC)，May 2007，Antalya，Turkey.2007(2):1390－1395.

［4］POPESCU M，CISTELECAN M V，MELCESCU L，et al.Low speed directly driven permanent magnet synchronous generators for wind energy applications［C］//IEEE International Conference on Clean Electrical Power(ICCEP)，May 2007.Capri，Italy.2007:784－788.

［5］CHEN Y，ZHU Z Q，and HOWE David.Three-dimensional lumped-parameter magnetic circuit analysis of single-phase fluxswitching permanent-magnet motor［J］.IEEE Transactions on Industry Applications，2008，44(6):1701 －1710.

［6］CHEN J T，ZHU Z Q.Influence of the rotor pole number on optimal parameters in flux-switching PM brushless AC machines by the lumped-parameter magnetic circuit model［J］.IEEE Transactions on Industry Applications，2010，46(4):1381 －1388.

［7］WANG D H，WANG X H.Analysis of static performance for flux-Switching motor by nonlinear equivalent magnetic circuit model［C］//International Conference of Electrical Machines and Systems(ICEMS)，Sep 2010，Korea.2010:1661－1665.

［8］CHEN J T，ZHU Z Q，HOWE D.A dual-lumped parameter magnetic circuit model accounting for the cross-coupling effect with particular reference to flux-switching permanent magnet machines［C］//International Conference on Power Electronics，Machines and Drives(PEMD)，Apr 2008，York，UK.2008:111－115.

［9］ZHANG G，CHENG M，HUA W.Analysis of flux-switching permanent-magnet machine by Nonlinear magnetic network model with bypass-bridges［C］//2010 International Conference on Electrical Machines and Systems(ICEMS)，Sep 2010，Korea.2010:1787－1791.