矩形永磁体空间磁场解析式推导及验证

1、长春理工大学机电工程学院 吕琼莹 杨柳 盛龙 周凌宇 2、93313部队 蒋贵德

1 引言

随着稀土永磁材料的不断涌现和应用领域的不断扩大，人们对永磁体的磁场计算更加关注。不同的应用领域所要求的永磁体的形状不同，对磁场的空间分布和磁场强度的要求也不同[1-4]。目前应用最多的是圆柱形、长方形、扇形和圆环形[1-2]等具有较高对称性的永磁体。本文描述了分子环流假说观点，并利用毕奥—萨伐尔定律对矩形永磁体空间三维场解析式进行推导并验证。

2 矩形永磁体分子电流理论

关于磁介质的磁化理论有两种不同的观点：磁荷观点[5]和分子电流观点。

2.1 安培分子电流假说

安培分子环流假说[6]：安培认为，在原子、分子等物质微粒的内部，存在着一种环形电流——分子电流，分子电流使每个物质分子都成为一个微小的磁体，它的两侧相当于两个磁极。对此，把环形电流产生磁场的知识和安培定则联系起来，就不难理解。值得注意的是，这两个磁极跟分子电流不可分割地联系在一起，因而磁极不能以单独的N极或S极存在。

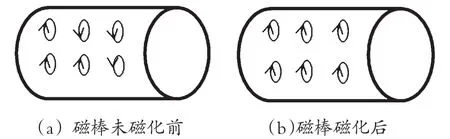
图1 安培分子环流模型

安培的分子电流假说揭示了磁性的起源，它使我们认识到磁铁的磁场和电流的磁场本质是一样的，都是由电荷的定向运动产生的。运动的电荷（电流）产生磁场，磁场对运动的电荷（电流）有磁场力的作用，所有的磁现象都可以归结为运动电荷（电流）之间通过磁场而发生的作用，这就是磁现象的电本质。

2.2 磁感应强度B与毕奥—萨伐尔定律

分子电流观点认为电流在其周围空间产生磁场，磁场再对其他电流发生作用，磁场矢量用磁感应强度B来描述。

根据毕奥—萨伐尔定律，在空间一点 P（x，y，z）产生的磁感应强度为：

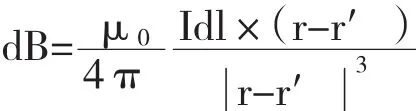
式中 r —源点（x0，y0，z0）矢径；

r —场点 P（x，y，z）矢径；

μ0—真空磁导率，μ0=4π×10-7H/m；

所以整个电流回路在P点产生的磁感应强度为：

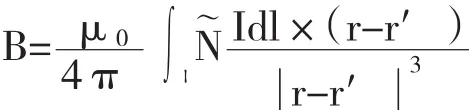
B的SI制单位为Wb/m2。

其电流强度为 I=Jdz，在 P（n，p，q）点处产生的场强为dB可视为由AB、BC、CD、DA段电流源产生的磁场叠加而成[9-10]。

AB 段在点 P（n，p，q）处产生的磁场强度为：

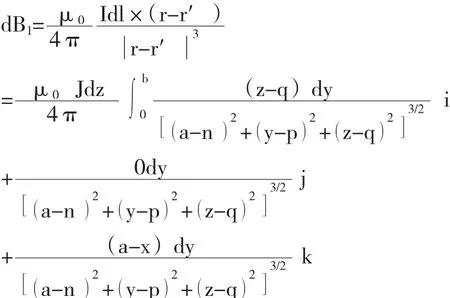
BC 段在点 P（n，p，q）处产生的磁场强度为：

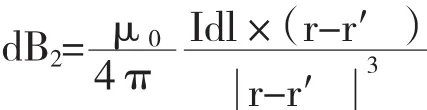
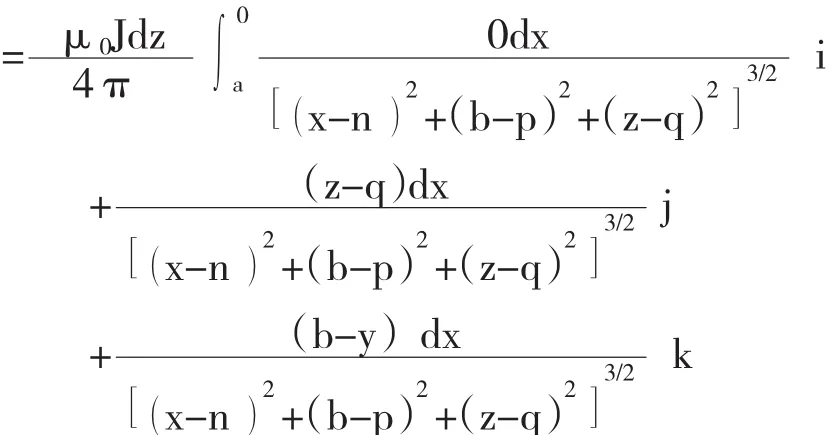
CD 段在点 P（n，p，q）处产生的磁场强度为：

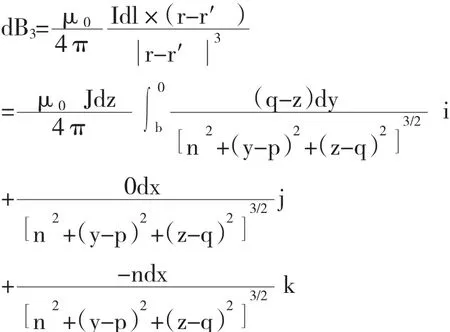
DA 段在点 P（n，p，q）处产生的磁场强度为：

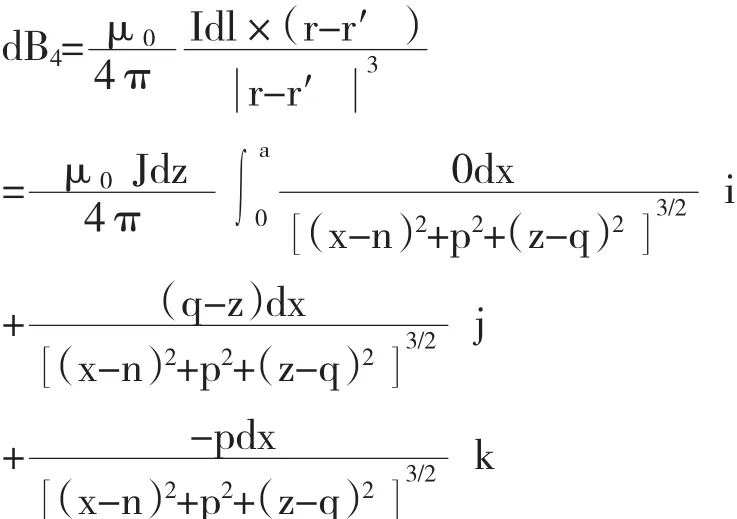
所以薄层电流环ABCDA在点P（n，p，q）处产生的总磁场强度为：

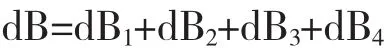
由于μ0、J均为已知常数，令K=，

则薄层电流环ABCDA在点P处的磁场分量为：

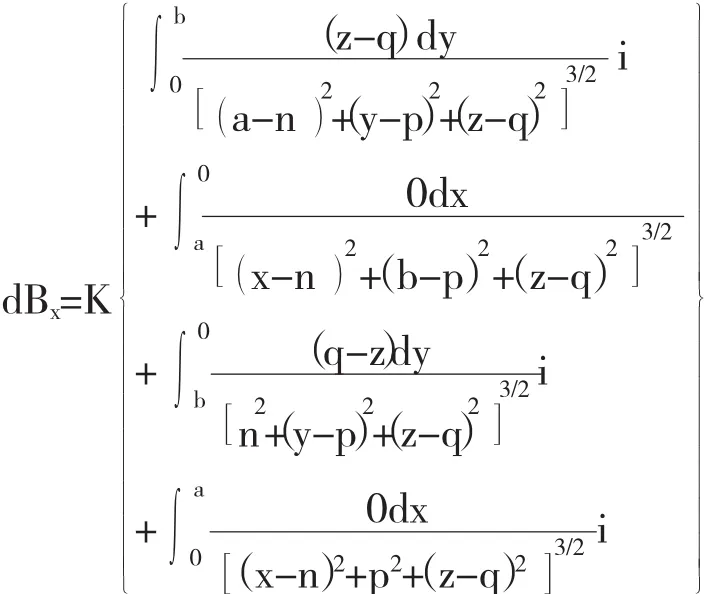
计算整理得:

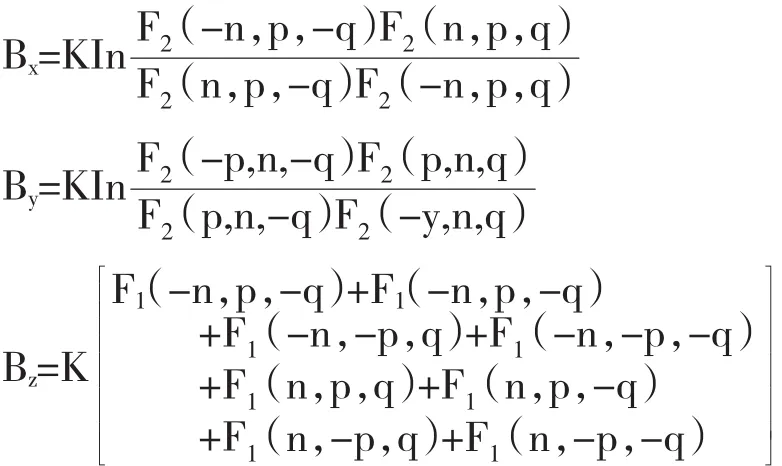
其中：

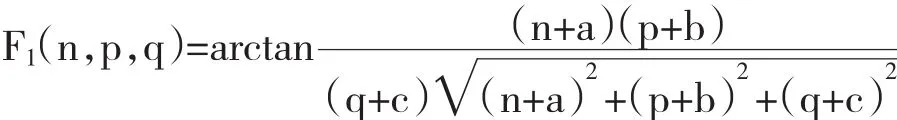
3 计算磁感应强度大小并验证解析式

3.1 MATLAB软件绘制磁感应强度曲面模型

运用MATLAB软件绘制磁体表面磁场强度，建立表面磁场强度的三维曲面模型。选取铷铁硼永磁体N50[11]。 规格如下：长×宽×高：a×b×c=40×30×10mm；剩磁 Br=1.40T（1T=104Gs），内禀矫顽力[10]HcJ=955kA/m，如图2所示。

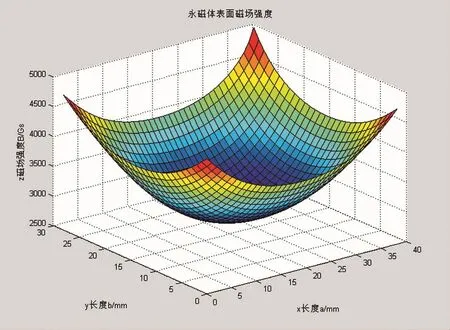
图2 MATLAB软件绘制磁体表面磁场强度

如图2所示，x，y轴表示永磁铁的长度和宽度。z轴表示永磁铁表面上任意一点的磁感应强度的大小。由此可得出：在磁体中心处的磁感应强度最小，磁体边缘处的磁感应强度最大。

3.2 ANSYS磁场模块对磁感应强度公式的验证

运用ANSYS分析软件中的电磁模块对上述永磁体进行分析，结果如图3所示。

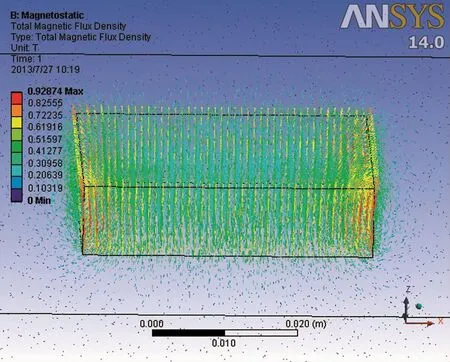
图3 ANSYS软件分析

如图3所示，根据ANSYS软件分析的结果可以看出，磁体的中心到边缘的磁感应强度的颜色变化是由蓝色逐渐过渡到红色，即磁感应强度有逐渐由小到大的变化趋势。磁体中心磁感应强度大小约为2000～3000Gs(1T=10000Gs)，与理论近似计算公式得出的结果相吻合。

可得出结论：在磁体厚度为3cm，长宽比为2.6时，磁体中心处的磁场强度最大。

4 结论

本文根据磁介质的分子电流观点，建立了矩形永磁体的分子环流理论模型。基于毕奥—萨伐尔定律，推导了该模型的三维磁感应强度解析表达式，并且运用MATLAB和ANSYS软件对此解析式进行了验证，与推导结果一致。

[1]王瑞凯；左洪福；吕萌.环形磁铁空间磁场的解析计算与仿真[J].航空计算技术，2006，41（5）：19-23

[2]王明勇；郎志坚. 方形磁体的空间磁场分布[J]. 磁性材料及器件, 2001, 32(6): 17-20

[3]李晓阳；徐金伟；刘宏娟.矩形永磁体三维磁场空间分布[J].北京工业大学学报，2008,34（1）：1-6

[4]苟晓凡；杨勇；郑晓静. 矩形永磁体磁场分布的解析表达式[J]. 应用数学和力学, 2004, 25(3): 23-34

[5]刘世明. 由磁荷观点分析均匀磁化介质球的磁场分布[J].电子科学, 2009, 13(7): 43-54

[6]赵普选；赵强；张考林. 安培分子电流假说思想的应用[J].物理与工程, 2003, 13(1): 12-24

[7]付林兴；邓志武. 毕奥-萨伐尔定律的推导[J]. 湘潭师范学院学报（自然科学版）, 2006, 28(1): 81-88

[8]贾兆平；刘惠恩. 磁场强度H与磁化电流之间关系的讨论[J].教学讨论

[9]刘宏娟.矩形永磁体三维磁场空间分布研究[D].北京工业大学.2006.5

[10]李景天；宋一得；郑勤红等.用等效磁荷法计算永磁体磁场[J].1999.4.19(2):33-36

[11]王臣；梁国君；杨文英等.永磁体磁特性参数测量分析方法的研究[J].机电元件.2009.6.2（29）：8-13