无阻力双星串行编队相对位置有限时间控制

张永合，梁旭文，张 健，胡庆雷

(1．中国科学院上海微系统与信息技术研究所，上海200050;2．上海微小卫星工程中心，上海201203;3．哈尔滨工业大学航天学院，哈尔滨150001)

0 引言

无阻力卫星具有通过自身无阻力控制回路消除外部保守力对卫星的影响的特点，在纯重力轨道下运行，能够实现卫星的超稳定控制。对于无阻力卫星的研究始于20世纪60年代，工程上一般可通过位移模式和加速度计模式实现卫星和其内部的质量块隔离，达到消除大气阻力等干扰的目的。文献［1］提出内嵌模型的设计思想，通过简化模型得到控制参数和分配指令，再由卫星的实际输出信号对其修正，取得良好的控制效果。文献［2］分析近地无阻力卫星的干扰模型，得到了带有干扰状态的卫星动力学增广系统，并设计了混合H2/H∞最优控制器，通过仿真校验了算法能够有效抑制干扰。近年来，欧美等航空技术先进国家，提出了采用无阻力卫星构成编队的协同工作方式，其中美国2002年发射的地球重力场测量卫星(GRACE)，欧空局的下一代重力卫星(NGGM)，激光干涉空间天线(LISA)等任务都采用了无阻力卫星编队控制的形式［3］。文献［4］采用频域方法对无阻力卫星编队的无阻力控制器与编队控制器输出信号进行讨论。无阻力卫星编队已经在深空探测、对地测量等空间科学领域中应用广泛，在航空科学研究与工程中承担了重要使命。本文以两颗无阻力卫星组成的串行编队为对象，研究该无阻力卫星编队在轨运行中相对位置控制问题。

在传统的卫星编队建模中，多采用主从式构型［5］，将主星作为建模坐标系的原点，并假设主星在理想情况下运动不需控制，分析从星相对于主星的运动，最终得到Clohessy－Wiltshire方程等编队运动模型。然而，这种假设在实际中难以保证，当主星受到不可忽略的扰动影响时，这种建模方法无法确保编队中的卫星运动到期望状态。文献［6］考虑了J2项摄动对主从卫星轨道的影响，给出了一组线性化的卫星编队动力学方程，并通过仿真校验该模型相比二体非线性模型具有更高的精度。对于无阻力卫星，虽然可以通过自身无阻力控制对外部环境干扰达到抑制作用，但仍存在一些不能完全消除的扰动，如加速度计测量偏差，推力器的噪声等，会引起编队卫星的星间距离变化。本文将以两颗无阻力卫星位置连线中点(可由GPS测量计算得到)为参考坐标系原点，考虑J2项摄动作用，分析两颗卫星相对原点的运动，推导出编队相对位置动力学模型并加以控制。

国内外学者针对卫星编队的协同控制、队形保持、交会对接等问题展开了研究。文献［7］针对主从式卫星编队，首先给出了最优参考轨迹，推导出相对该轨迹的跟踪误差模型，并进一步设计了鲁棒自适应控制器。文献［8］在编队中卫星速度不可测量情况下，考虑质量不确定性以及外界干扰作用，提出了一种高增益观测器，获取上述状态的精确观测值，并设计了输出反馈控制算法。文献［9］针对电磁卫星编队，考虑了摄动干扰和输入时延等问题，设计了滑模变结构控制器，实现了高精度的相对位置控制。注意到，上述文献中的控制器都只能保证系统渐近稳定于期望状态，对系统的收敛速度要求较低。近年来，随着控制理论的发展和软硬件水平的提高，有限时间控制算法受到了关注，并在提高系统的响应速度和抗干扰能力方面体现出优势。文献［10］考虑导弹末端制导问题，设计了连续的有限时间制导律，并通过引入线性反馈项，提高了系统在距原点较远处向平衡点趋近的速率。文献［11］考虑电磁卫星编队的轨迹跟踪，采用终端滑模方法，提出了有限时间控制算法。文献［12］以小行星登陆车为对象，基于视线坐标系建模，根据齐次系统理论设计了有限时间控制器。

本文首先定义无阻力卫星编队相对位置建模的参考坐标系，给出了无阻力卫星编队的相对位置数学模型。针对该相对位置模型，提出了带有自适应参数辨识的有限时间连续控制算法。本文设计的实际有限时间控制器能够保证闭环系统的快速稳定，同时利用对卫星质量的参数自适应估计使本文的算法不依赖于确定已知的卫星质量，保证了系统的鲁棒性。

1 基础知识

1．1无阻力卫星编队相对运动模型

本文考虑由两颗无阻力卫星组成的串行编队，图1中为无阻力卫星编队相对位置控制系统框图。卫星在轨运动的位置和速度信息由GPS实时测量得到。卫星可以通过自身的无阻力控制抵消太空环境中的大气阻力等干扰，但对于高频扰动的消除能力有限，因此存在无阻力控制残差。相对位置控制系统与卫星无阻力控制分别独立设计，无阻力控制的残差以及卫星的推力装置噪声对卫星位置控制存在干扰。由控制器计算得到的控制输出量将平均分配到两颗卫星的推力装置。

图1 无阻力双星编队相对位置控制系统示意图Fig．1 Relative position control system for drag－free dual－satellite formation

图2 无阻力双星编队飞行示意图Fig．2 Drag－free dual－satellite formation flying

图2为编队在轨飞行示意图，图中黑色实线定义为近圆的参考轨道，遵循二体轨道规律。现实中，单颗卫星无阻力的控制不可能完全抵消外界干扰，存在无阻力控制残差，记为δr。无阻力控制残差将引起卫星的运动会偏离原参考轨道。通过GPS测量两颗卫星的位置，可计算得出两颗卫星位置连线中点C，且C点的运动轨迹相对于由参考轨道中C－点的偏移由扰动矢量δr引起。虚线表示双星位置连线的中点C运动形成的轨迹。以位置中点C为原点建立参考坐标系，x轴沿卫星速度方向，y轴沿轨道法向，z轴符合右手定则。两星相对位置矢量Δr符合 Δr=δr1－ δr2，δr1与 δr2分别为两星相对于原参考轨道上C－点的位置矢量。rc－为C－点相对地心OI的矢量，r1、r2分别为两卫星相对于地心的矢量。首先，考虑卫星1相对于C－点的加速度方程［13］

考虑二体运动和J2项扰动，参考轨道上C－点的加速度为=g0(rc－)+J2(rc－)。其中，g0(rc－)表示无扰动下C－点的加速度，J2(rc－)表示由J2项引起的C－点加速度。J2(rc－)由平均值g2(rc－)和周期项δg2(rc－，θ)组成。于是，卫星1相对于C－点的加速度可分解为

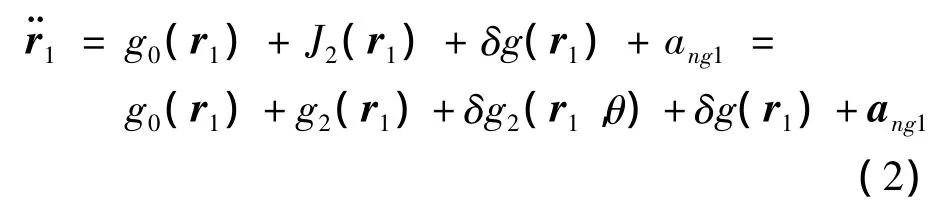
式中:g0(r1)表示无扰动下卫星1的加速度，J2(r1)表示由J2项引起卫星1的加速度，由平均值g2(r1)和周期项δg2(r1，θ)组成，δg(r1)表示其他高阶摄动力，ang1为非重力加速度。将在C－点线性展开可得

式中:▽g0(rc－)，▽J2(rc－)分别表示重力加速度和J2摄动项在C－点的梯度函数，▽g0(rc－)与▽J2(rc－)的具体形式如下［13］

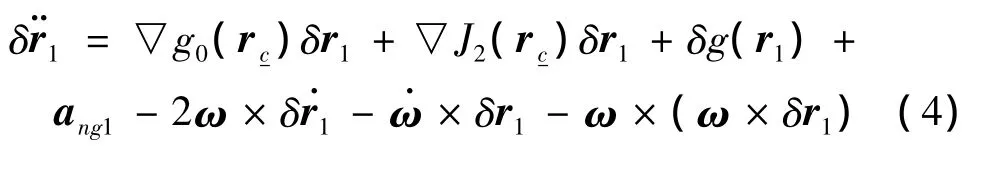
若以两星位置连线中点C作为参考点，得到δr1的加速度方程为

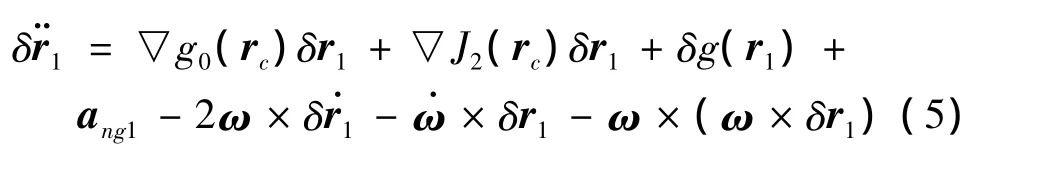
式中:▽g0(rc)，▽J2(rc)表示重力加速度和J2摄动项在C点的梯度函数。根据两星相对位置Δr=δr1－ δr2，δr2加速度方程形式与式(5)类似，整理得两星相对位置Δr加速度方程

两颗无阻力卫星之间相对位置 Δr=［x y z］T，式(6)中 Δg=δg(r1)－ δg(r2)表示除J2项外的其他高阶摄动力，Δang=Δang1－Δang2为非重力加速度，由于Δg和Δang在实际中为很小的数值，因此可以忽略，得以下方程

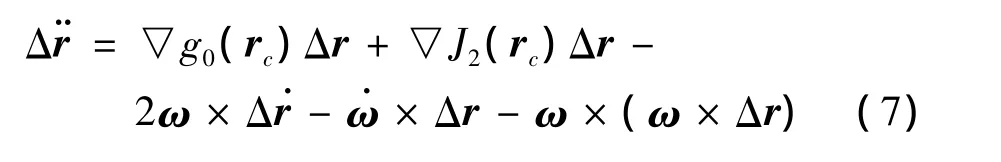
最终，得到无阻力双星编队的相对位置动力学模型表示如下:

式中:ρ=［x y z］T表示相对位置矢量Δr，卫星质量m为未知常数。i为轨道倾角，由于考虑J2摄动的影响，轨道平均角速度为，其中，经整理，矩阵A和B具体形式如下，

注1．用于测量重力场的无阻力卫星编队，一般在低地轨道飞行，建立更为精确的动力学模型，需考虑J2摄动产生的影响。

注2．显然，式(9)中A矩阵为反对称阵。

注3．区别于传统主从式卫星编队模型，本文以两颗无阻力卫星位置连线中点为原点建模，将计算得到的控制量平均分配到两个卫星上，控制两星相对位置达到期望状态，平衡了两颗卫星的能量消耗。

1．2相关引理

引理1．［15］考虑下面的系统

其中，f:U0×R+→Rn在原点x=0的开邻域U0上是连续的。如果有一个正定函数)(定义在×R+上，其中¯U⊂U0⊂Rp是原点的一个邻域)，实数c＞0和0＜α＜1，使得在上半负定，则(x)在有限时间内逼近于0。并且，该有限时间T满足

引理2．［16］考虑系统=f(x，u)，假设存在连续函数(x)，标量φ＞0，0＜φ＜1和0＜ϑ＜∞ ，0＜σ≤1，0＜σ0＜1，则

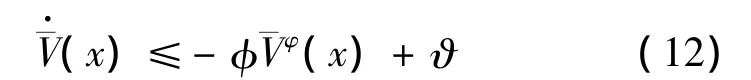
引理3．［17］对于∀x∈R和∀y∈R，若p1和p2为正奇数，则

引理4．［17］对于∀x∈R和∀y∈R，若c＞0和d＞0，则有

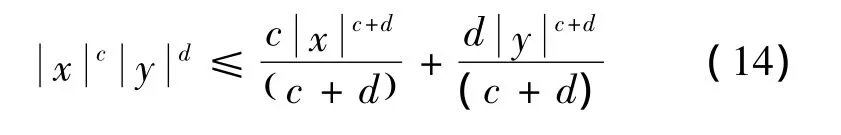
引理5．［18］∀x∈R，i=1，2，…，n，有实数m∈(0，1］，以下不等式成立

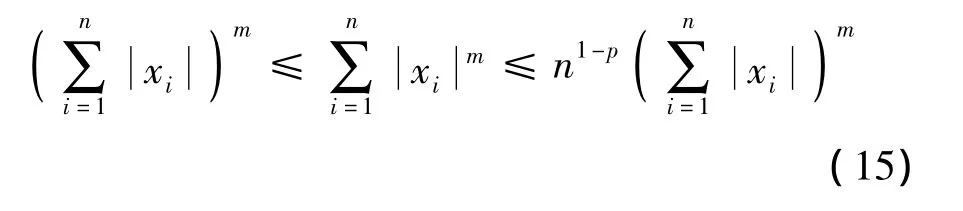
2 无阻力卫星编队相对位置有限时间控制

无阻力卫星编队在航天工程中得到了广泛的应用，卫星编队队形的保持和重构对于航天任务起到关键作用，特别是在某些军事侦察任务中，能否快速精确地形成期望队形捕捉目标决定了编队任务的成败。另外，在轨运行卫星往往受到质量不确定性、外部干扰等影响，虽然无阻力控制系统对于太阳光压、大气扰动等干扰力有抑制效果，但不能保证完全消除环境干扰以及自身工作噪声的扰动。因此，本文提出了带有自适应参数辨识的卫星编队相对位置有限时间控制算法，使得系统在有限时间内收敛到期望状态，并且克服了质量不确定性，保证了系统的鲁棒性和精确性。

定理1．考虑无阻力双星编队相对运动模型(8)，假设卫星的质量m为不确定常数，设计有限时间控制器(16)及参数自适应更新律(17)

则闭环系统实际有限时间稳定，即两颗卫星之间相对位置ρ在有限时间内收敛到期望位置ρd的有界邻域内，且收敛时间为

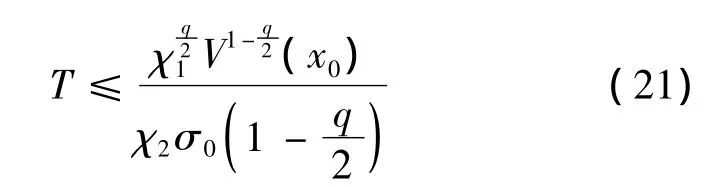
式中:0＜ σ0＜1，θ1，χ1，χ2，q和V将在证明过程中定义。

证．两颗卫星之间的期望相对位置由ρd表示，则相对位置误差为ρe=ρ－ρd，期望的相对位置ρd为常数，因此首先，为使相对位置误差收敛到0，取Lyapunov函数V1，

对式(22)求导数，并令ρe=v，则

(23)进一步简化为

将式(24)代入式(23)得

取V2i形式如下

由文献［17］可知，V2i为正定函数，对式(26)求导得

注4．在有限时间控制问题中，较多采用终端滑模设计有限时间控制器，由于含有符号函数项，造成系统存在抖振。本文所设计的控制器在理论上是连续反馈控制，然而，实际系统长时间工作在小信号区，该控制器仍难以实现连续控制。设计能够克服系统抖振的控制器，依然是值得研究的问题。

3 仿真及分析

本文针对两颗无阻力卫星构成的串行编队进行数字仿真，取单颗的无阻力卫星质量m=300 kg，两星初始相对位置 ρ0=103×［9．55 0．43－0．52］Tm，期望相对位置为ρd=103×［10 0 0］Tm。卫星轨道为太阳同步轨道，轨道半长轴为6730 km，轨道倾角i=97°，偏心率为0．001，升交点赤经为0°，近地点幅角为45°，初始时刻参考点真近点角为70°。仿真中，高频干扰d采用高斯白噪声 Ξ(0，δp)，Ξ(0，δp)表示均值为0，方差为δp=0．01的高斯白噪声信号。

图3 两颗卫星相对位置仿真曲线Fig．3 Response curves of relative position between two satellites

考虑本文相对位置模型(8)，有限时间控制器(16)及自适应更新律(17)，取p=15/13，λ=0．02，k1=0．004，k2=0．5，得到仿真结果如图3～图5所示。图3为两星相对位置误差曲线(ρe=ρ0－ρd)，在无干扰情况下，两星相对位置在2000 s收敛到期望值，并在3000 s以后精度达到±0．1 m。当高频干扰d存在的情况下，两颗卫星相对位置达到期望值的所用时间约为2000 s，并且仍能保持在±2 m的允许误差范围内。图4为两星相对速度曲线。图5为控制力曲线，控制输出幅值在范围内，并且高频干扰没有引起控制量最大幅值显著变化，所设计的控制器具有良好的干扰抑制能力。

图4 两颗卫星相对速度仿真曲线Fig．4 Response curves of relative velocity between two satellites

4 结论

图5 控制力仿真曲线Fig．5 Response curves of total control force

本文针对两颗无阻力卫星构成的串行编队相对位置控制问题，设计了实际有限时间控制器。首先，选取了两星位置连线中点作为参考坐标系原点，建立了相对位置动力学模型。基于该模型，提出了带有自适应参数辨识的有限时间控制器，利用对卫星质量的估计值得到了使闭环系统实现有限时间控制算法。仿真结果表明，该算法能够使无阻力双星编队的相对位置在短时间内运动至期望值，并且闭环系统具有较好的鲁棒性。

［1］Canuto E，Bona B，Indri M，et al．Drag free control for the European satellite GOCE，part ii:digital control［C］．The 41st IEEE Conference on Decision and Control，Las Vegas，Nevada USA，Dec．10－13，2002．

［2］ 曹喜滨，施梨，董晓光，等．基于干扰观测的无阻力卫星控制器设计［J］．宇航学报，2012，33(4):411－418．［Cao Xi－bin，Shi Li，Dong Xiao－guang，et al．An adaptive control law for autonomous formation flight［J］．Journal of Astronautics，2012，33(4):411－418．］

［3］ 张锦绣，曹喜滨，董晓光，等．无阻力卫星编队的发展现状和趋势研究［J］．哈尔滨工业大学学报，2010，42(5):673－677．［Zhang Jin－xiu，Cao Xi－bin，Dong Xiao－guang，et al．Development status and tendency of drag－free satellite formation flying［J］．Journal of Harbin Institute of Technology，2010，42(5):673－677．］

［4］Theil S，From M，Pettazzi L，et al．Formation of drag－free satellites［C］．The 56th International Astronautical Congress，Fukuoka，Japan，Oct．17－21，2005．

［5］Kristiansen R，Grøtli E，Nicklasson P，et al．A model of relative translation and rotation in leader－follower spacecraft formations［J］．Modeling，Identification and Control，2007，28(1):3－13．

［6］ 杏建军，时伟，蒋炳炎．J2项摄动条件下线性化的编队卫星动力学方程［J］．宇航学报，2013，34(5):605－610．［Xing Jian－jun，Shi Wei，Jiang Bing－yan．Linearized formation flight dynamics model under J2perturbation［J］．Journal of Astronautics，2013，34(5):605－610．］

［7］ 董晓光，曹喜滨，张锦绣，等．卫星编队飞行的鲁棒自适应控制方法［J］．自动化学报，2012，38(5):132－141．［Dong Xiao－guang，Cao Xi－bin，Zhang Jin－xiu，et al．A robust adaptive control law for satellite formation flying［J］．Acta Automatica Sinica，2012，38(5):132－141．］

［8］Lee K，Singh S．Adaptive output feedback spacecraft formation flying via observer based feedback linearization［C］．51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition，Grapevine，Texas，USA，Jan．7－10，2013．

［9］ 苏建敏，董云峰．电磁卫星编队位置跟踪滑模变结构控制［J］．宇航学报，2011，32(5):1094－1099．［Su Jian－min，Dong Yun－feng．Sliding mode variable structure control for electromagnetic satellite formation station－tracking［J］．Journal of Astronautics，2011，32(5):1094－1099．］

［10］ 丁世宏，李世华，罗生．基于连续有限时间控制技术的导引律设计［J］．宇航学报，2011，32(4):727－733．［Ding Shihong，Li Shi－hua，Luo Sheng．Guidance law design based on continuous finite－time control technique［J］．Journal of Astronautics，2011，32(4):727－733．］

［11］Zeng GQ，Hu M．Finite－time control for electromagnetic satellite formations［J］．Acta Astronautica，2012，74:120－130．

［12］Lan Q X，Li S H，Yang J，et al．Finite－time control for soft landing on an asteroid based on line－of－sight angle［J］．Journal of the Franklin Institute，2014，351(1):383－398．

［13］Canuto E，Molano－Jimenez A，Perez－Montenegro C，et al．Longdistance，drag－free，low－thrust，LEO formation control for earth gravity monitoring［J］．Acta Astronautica，2011，69(7－8):571－582．

［14］Schweighart SA，Sedwick R J．High－fidelity linearized J2model for satellite formation flight［J］．Journal of Guidance，Control，and Dynamics，2002，25(6):1073－1079．

［15］Bhat S P，Bernstein D S．Finite－time stability of continuous autonomous systems［J］．SIAM Journal on Control and Optimization，2000，38(8):751－766．

［16］Zhu Z，Xia Y Q，Fu M Y．Attitude stabilization of rigid spacecraft with finite－time convergence［J］．International Journal of Robust and Nonlinear Control，2011，21(6):686－702．

［17］Qian C J，Lin W．A continuous feedback approach to global strong stabilization of nonlinear systems［J］．IEEE Transactions on Automatic Control，2001，46(7)，1061－1079．

［18］Hardy G，Littlewood J，Polya G．Inequalities(1st ed)．［M］．Cambridge:Cambridge University Press，1952．