基于相似性的高光谱海冰图像的波段选择研究

张 龙 ，韩彦岭 ，张 云 ，袁国良

（1.上海海事大学 上海 201306；2.上海海洋大学 上海 201306）

海冰是影响极地乃至全球气候系统的一个重要因子[1]，因此研究极地海冰变化成为气候研究的重要方向。与常规的观测手段相比，高光谱遥感技术可以及时有效地获取海冰变化的详细信息以及海冰接近连续的光谱信息，为极地海冰检测及重要信息的获取提供了重要手段。然而，高光谱数据量大，波段多且窄，波段之间相关性强，信息冗余度较高。一方面数据量的剧增给数据的处理和解译带来很多问题；同时波段之间的相关性和冗余信息对传统的图像分类算法提出了巨大挑战。因此，有必要对高光谱海冰数据进行降维处理。现有的降维方法有基于特征提取和基于波段选择两种方法，而波段选择方法可以保持图像的原有特性，更有利于对图像进行分析，成为高光谱降维的重要研究方向。目前已经提出的波段选择算法很多，具体分为监督波段选择和非监督波段选择两类，非监督波段选择方法不需要有关地物类型的先验知识，更符合遥感图像处理的实际情况，在遥感图像处理中有着广泛的应用。

非监督波段选择的基本思路是选择具有代表性的波段子集，使得该子集内的波段间相关程度最小且各波段自身信息量尽量大[2]。目前对非监督波段选择的研究很多，如基于信息理论的波段选择算法[3]等。但这些方法存在缺点，例如熵只考虑了波段的信息量，忽略了波段间的相关性使得所选择的波段子集不一定最优。应用于衡量不同像元间光谱相似性度量的方法[4]，如光谱相关性度量（SCM），光谱信息散度（SID）和波谱角 （SAM）、以及结合SID和SAM优点的混合度量方法SID_SAM[5]等在光谱识别方面取得较好的效果。因此，本文提出将这些基于光谱相似性度量的方法应用于高光谱海冰图像的非监督波段选择中，利用光谱相似性度量比较波段间的不相似性，首先以熵最大的波段开始，然后采用SCM和SID_SAM方法进行初始波段选择，再通过LP算法进行后续波段选择，为了确保选出信息量较大，又有区别性的波段，数据需要进行预处理，例如，确定针对高光谱海冰数据可分性较好的波段范围、移除坏波段等。另外，波段选择过程中像素选择的影响，需要选择的波段数本文也进行了分析研究，并通过一些已广泛运用的波段选择算法，如熵（ENTROPY），一阶光谱导数（FSD）[6]进行对比分析，实验结果表明，就分类性能而言本文提出的方法优于其他传统方法。

1 基于相似性的波段选择算法

基于相似性的波段选择是在考虑波段信息量的基础上，尽量选择相似性低的波段。该算法包括两个过程：先通过计算单波段之间的相似度进行初始波段选择，从而选出最不相似的两个波段；然后联合计算单波段与多波段之间的相似度进行后续波段选择，从而能够从整个波段空间选择相似性最小的波段组合。

1.1 初始波段选择算法

假设原始高光谱图像有M个波段，初始波段选择算法的基本步骤如下：

1）结合海冰的光谱特征，以随机的或者熵最大的波段B1初始化算法。

2）从剩下的M-1个波段中找到与波段B1最优的组合波段B2，B2与B1最不相似。

3）从剩下的M-1个波段中找到与波段B2最优的组合波段B3，B3与B2最不相似。

4）如果B3＝B1，则证明B1和B2为最不相似的波段组合，此时，算法中止执行。如果B3≠B1，继续执行下一步。

5）继续执行算法直到Bi+1＝Bi-1为止，然后将选择的波段Bi-1或者Bi作为初始波段（或者将二者作为初始波段对）。

采用的两种初始波段选择算法定义如下：

1）SID:由辐射或者反射的性质，假设波段B中所有的分量都是非负的，光谱信息散度定义如下：假设波段B1对应像素概率为 q =（q1，q2，…，qL），其中：qi=b1i/相应的可得到波段 B 2 对应像素概率为 p =（p1，p2，…，pL），其中：由信息理论得到波段B2关于波段B1的相对熵：

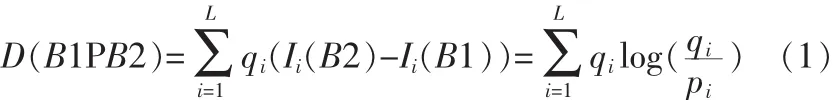
B1关于B2的相对熵为：

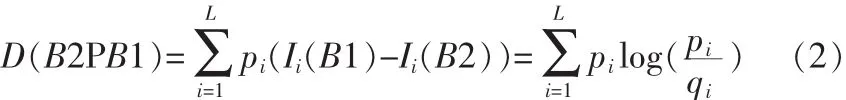
则两个波段之间的光谱信息散度定义如下：

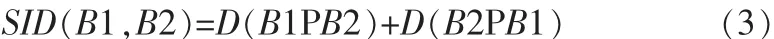
其中，Ii（B1）和 Ii（B2）为波段 B1 和 B2 在第 i个分量上的自信息，越小的度量值表明了两个波段之间越大的相似性。

2）SAM：两个波段的波谱角定义如下：

SID 与 S AM的混合度量有 S ID×sin（SAM）和 S ID×tan（SAM）两种[5]，都取得了比较好的评价结果，本文选择前者。

3）SCM:假设波段B1和B2为集合Φ中的两个波段B1=（b11，b12，…，b1L），其中波段和波段 B 2=（b21，b22，…，b2L），则两个波段之间的相关性度量：

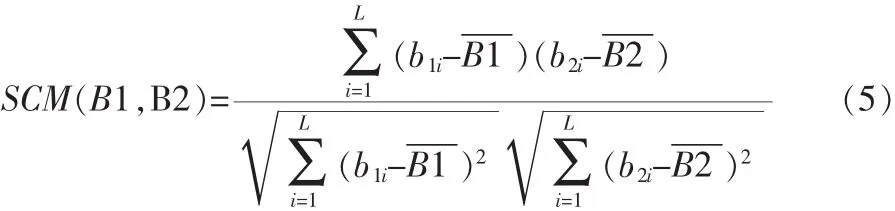
1.2 后续波段选择算法

后续波段选择算法的基本步骤如下：

1）以选择的初始波段B1开始，初始化算法，得到选择的波段子集Φ={B1}。

2）由确定的算法，找到与B1最不相似的波段B2，此时选择的波段子集更新为Φ=ΦU{B2}。

3）继续执行第二步，直到子集Φ中选择的波段数目满足要求为止。

采用的后续波段选择算法定义如下：

LP:假设波段B1，B2为子集Φ中的两个波段，为了找到与波段B1和B2最不相似的波段B，B1和B2可以用来估计波段B:

其中B′，为使用波段B1和B2对波段B的估计或者线性预测，a0，a1和a2是最小化线性预测误差的参数，误差：emin=PB-B′P，参数向量 a=（a0，a1，a2）T可以由最小二乘解来确定：

其中，x为L×3矩阵，第一列均为1，第二列包含波段B1的所有选择像素，第三列包含波段B2的所有选择像素，y为包含波段B的所有选择像素的L×1向量。则获得最大误差emin的波段被认为与波段B1、B2最不相似，作为波段B3选入子集Φ中，很显然，继续执行算法可以继续选择波段，直到子集Φ中选择的波段数目满足要求为止。

2 波段选择过程中相关问题分析

2.1 像素选择

由于高光谱的波段图像之间具有很高的空间相关性，为了减少计算量提高波段选择的效率需要对像素进行选择。选择的像素数目和像素位置往往对波段选择算法的性能影响很大，因此本文中对不同的像素选择方法做了对比分析。

1）选择像素的数目：首先选择所有像素进行波段选择，然后分别选择1%的像素和1‰的像素进行对比分析。

2）选择像素的位置：为了消除随机选择像素时可能无法包含所有类别像素的影响，本文提出基于k_means聚类的像素选择方法，具体步骤如下：

①选择所有原始波段 （坏波段移除后）进行k_means聚类，合并相同类别。

②对不同类别的数目和位置进行统计，确定每类要选择的像素数目。

③根据②，均匀的选择相应类别的像素，直到每类像素的数目满足要求为止。

通过实验分析发现，基于k_means聚类的像素选择方法能够根据不同类别的像素所占比例，选择相应的像素，为了对不同波段选择算法的性能进行分析，可以存储选择的像素，从而提高分析的可靠性。

2.2 选择的波段数

实际应用中很难确定需要选择的波段数，根据经验，如果图像场景很复杂包含较多的类别时就需要选择较多的波段，这是因为数据的维度应该足够高以容纳这些类别用于检波或者分类[2]。高光谱图像中不同信号源的最小数目可以使用虚拟维度（VD）来估计[7]。虚拟维度估计方法中，一般情况下，噪声子空间投影（NSP）获得了最大的估计，结果可以作为需要选择波段数的一个参考值。

2.3 性能评价

为了对选择的波段信息量和类可分性进行评价，文中分别采用支持向量（SVM）进行监督分类和k_means进行非监督分类用于结果分析。当没有可利用的像素级的真实地表信息时，来自于所有原始波段的分类图可被看作真实地表，来自于选择波段的分类图可以用空间相关系数ρ与该真实地表进行对比，平均相关系数ρ越趋近于1意味着越好的分类结果。该方法是基于针对类别相似但光谱可分离情况下的一种合理假设[8]：使用所有的原始波段（坏波段剔除后），可得到一个很好或者至少令人满意的分类性能。这种基于图像相似性的方法在非监督情况下或者缺少像素级地表真实图像的情况下，可以给出定量的评价。

3 实验分析

实验采用2014年4月12日采集的左上角经纬度74°1′10.93″N，79°47.22″W， 右 下 角 经 纬 度 73°2′12.71″N，80°5′33.86″W，具有 242个波段，大小为 3233×256海冰类型较容易判别EO-1高光谱海冰图像。图像中的地物类别主要有4类：厚冰，薄冰，海水和积雪。

3.1 数据的预处理

为了选择信息量较大又有区别性的波段，水汽吸收波段和低信噪比波段需要先移除，这是因为这些波段虽然不相似，但是几乎不包含有用信息[2]。EO-1高光谱遥感L1产品数据包含242个波段，剔除受水汽影响、未经过辐射定标处理和重叠的波段后，剩下176个波段，即：8至57、79至120、128 至 166、179 至 223[9]。

由北极海冰的反射率特征[1]和实验中高光谱海冰图像的海冰反射率特征可以确定选择波段的波长范围为400~1 350 nm。包含在此波长范围的已选择波段为8至57和79至120，共92个波段作为波段选择的原始波段。

3.2 选择的波段数

表1列出了在给定不同虚警概率情Pf况下由NSP得到的虚拟维度的估计：

表1 NSP得到虚拟维度的估计Tab.1 VD estim ates obtained by the NSP method

如表1所示，在给定不同虚警概率时VD的值均为4，在后面的分析中，将此作为需要选择波段数的一个参考值。

3.3 像素选择的影响

实验中，通过随机选择1%的像素，k_means法选择1%像素，k_means法选择1‰像素和选择所有像素分别进行波段选择以进行对比分析。

图1展示了不同像素条件下，SCM+LP选择的波段进行监督和非监督分类结果与使用所有原始波段 （坏波段移除）对应分类图之间的平均相关系数。如图1（a）所示，在k_means选择1‰的像素时，SCM+LP选择4个波段的监督分类平均相关系数0.9861，选择8个波段的监督分类平均相关系数为0.9864，分类精度只有细微的提高，而波段数却增加了一倍。同时随着选择波段数的增加，分类精度也几乎没有变化。因此，虚拟维度的值VD=4在选择合适的波段数目上给出了合理的预测，它可以在分类精度与所需降低的数据维数之间取得平衡。由图1（a-b）可知k_means法选择1%像素时选择波段的分类精度与使用所有像素选择波段的分类精度几乎相同。同时k_means法选择1‰像素时，SCM+LP选择波段的分类精度是最高的，这表明了k_means法是一种非常有效的像素选择方法。

在随机选择像素的情况下，由于选择的像素的变化，选择的波段也随之变化很大，更重要的是，随机选择像素时不能保证所选择的像素总能包含所有类别，尤其是像素较少的类别。相比较而言，k_means法选择的像素总能包含不同类别的像素，在进行重复选择时所选择的波段号是固定不变的，便于对不同算法进行对比分析。需要指出的是，当k_means选择0.1‰像素时，由于聚类误差的存在，选择像素太少时降低了波段选择算法的性能，因此这里不再讨论。

3.4 波段选择算法的性能评价

由3.3中的结果，这里仅对1‰像素的波段选择结果进行对比分析。图2给出了92个原始波段的熵，如图2所示，第33个波段即40号波段的熵最大，在后面的分析中，将此作为选择初始波段的起始波段。图3为各个算法选择波段的监督和非监督分类结果与所有原始波（坏波段移除后）对应分类图之间的平均相关系数。

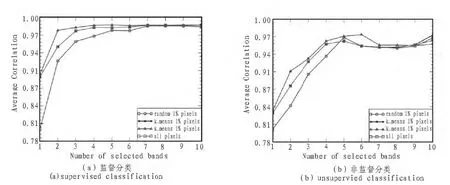
图1 SCM+LP选择波段性能（所有像素，随机选择1%，k_means选择1%和k_means选择1‰）Fig.1 The performance analysis of band selection based on SCM+LP（Comparison between using all pixels， 1%pixels with random selection pixels，1%pixels with k_means and 1‰ pixels with k_means）

如图3所示，虽然ENTROPY+SCM和ENTROPY+SID_SAM选择初始波段的分类精度要低于ENTROPY和FSD，但是随着选择波段数的增加，分类精度均高于后二者。LP在选择3个波段时，分类精度也高于后二者。选择6个波段时，三者分类精度均收敛。因此，就整体而言ENTROPY+SCM+LP、ENTROPY+SID_SAM+LP和LP选择波段的分类精度是最好的，这说明了三者的波段选择性能要优于ENTROPY和FSD。同时，本文提出的方法ENTROPY+SCM+LP获得了最高的评价，分类精度优于ENTROPY+SID_SAM+LP和传统的LP算法。ENTROPY+SCM+LP在选择4个波段时，分类精度已经收敛，监督分类平均相关系数为0.98几乎接近于1，但是数据的维数由92降到了4。

图2 所有波段的熵Fig.2 The entropy of all bands

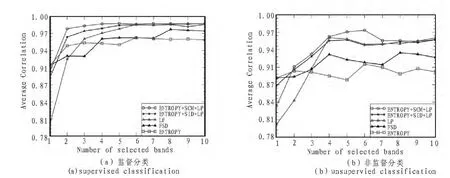
图3 ENTROPY+SCM+LP，ENTROPY+SID_SAM+LP，LP，FSD和 ENTROPY的分类精度对比（k_means选择1‰像素）Fig.3 Comparison on classification accuracy for ENTROPY+SCM+LP，ENTROPY+SID_SAM+LP，FSD and ENTROPY methods（1‰ pixels selected by k_means）

4 结 论

本文从极地海冰光谱特性出发，针对不同海冰类型在可分性较好的波段上进行波段选择，将基于波段相似性度量的非监督波段选择算法应用于高光谱海冰检测，根据实验结果分析，所研究方法，在考虑波段信息量的基础上找出最不相似的波段，大大提高波段选择效率的同时获得较高的分类性能。主要贡献如下：1）考虑到极地海冰的光谱特征，选择光谱特征明显且可分性较好的波段应用到高光谱图像的波段选择过程，可以有效缩减原始波段范围，提高算法效率的同时选出信息含量比较高的波段。2）考虑到高光谱图像较高的空间相关性，采用基于k_means聚类的像素选择，分析以不同比率选择像素情况下分类精度的变化，得出基于k_means聚类的1‰像素选择可以兼顾效率与性能的平衡，在降低像素数目的同时保证了较高的分类性能。3）将光谱相似性度量方法应用于高光谱海冰图像的初始波段选择中，分析了不同的初始波段算法与后续波段算法组合的性能，本文提出的ENTROPY+SCM+LP方法获得了最高的评价，能够有效应用于高光谱海冰图像的数据降维。

[1]柯长青，谢红接，雷瑞波，等.北极海冰的光谱特征分析[J].光谱学与光谱分析，2012，32（4）:1081.KE Chang-qing，XIE Hong-jie，LEI Rui-bo，et al.Analysis of the spectral characteristicsof the arctic sea ice[J].Spectroscopy and Spectral Analysis，2012，32（4）:1081.

[2]Du Q，Yang H.Similarity-based unsupervised band selection for hyperspectral image analysis[J].Geoscience and Remote Sensing Letters， IEEE，2008，5（4）:564-568.

[3]Martínez-UsóA，Pla F，Sotoca J M，et al.Clustering-based hyperspectral band selection using information measures[J].Geoscience and Remote Sensing， IEEE Transactions on，2007，45（12）:4158-4171.

[4]Kong X，Shu N，Huang W，et al.The research on effectiveness of spectral similarity measures for hyperspectral image[C]//Image and Signal Processing （CISP）， 2010 3rd International Congress on.IEEE，2010，5:2269-2273.

[5]Du Y，Chang C I，Ren H，et al.New hyperspectral discrimination measure for spectral characterization[J].Optical Engineering，2004，43（8）:1777-1786.

[6]Bajcsy P，Groves P.Methodology for hyperspectral band selection[J].Photogrammetric Engineering&Remote Sensing，2004，70（7）:793-802.

[7]Chang C I，Du Q.Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J].Geoscience and Remote Sensing， IEEETransactionson，2004，42（3）:608-619.

[8]Platt R V，Goetz A F H.A comparison of AVIRIS and Landsat for land use classification at the urban fringe[J].Photogrammetric Engineering&Remote Sensing，2004，70 （7）:813-819.

[9]谭炳香，李增元，陈尔学，等.EO-1 Hyperion高光谱数据的预处理[J].遥感信息，2006（6）:36-41.TAN Bing-xiang，LI Zeng-yuan，CHEN Er-xue，et al.EO-1 Hyperion hyperspectral data preprocessing[J].Remote Sensing Imformation，2006（6）:36-41.