基于可靠度理论的无机胶植筋设计方法

丁红岩 ，梁玉国，2，高天宝

（1. 天津大学建筑工程学院，天津 300072; 2.河北省建筑科学研究院，河北 石家庄 050021; 3.天津城建大学能源与安全工程学院，天津 300384）

混凝土植筋锚固技术已成为现代建筑技术的重要组成部分，主要应用于工程结构的维修、加固以及混凝土新增结构构件连接等方面，可以有效地解决新老混凝土连接、钢筋漏埋、错埋等钢筋生根问题[1]．目前，国内外已开展了一些植筋技术的研究工作，相关研究主要集中在不同埋深下化学植筋单筋受拉承载力、破坏形态、粘结滑移以及增层改造工程中常见的植筋梁柱试件抗震性能等方面，并取得了一定的成果[2-5]．关于植筋的可靠度研究方面，主要集中在化学植筋的可靠度分析上[6]．无机胶植筋与化学植筋相比具有如下优点：成本低，损耗小；强度的热稳定性、抗惨性、护筋性能良好；耐老化性与混凝土构筑物本体一致；施工简便[7]．因此，无机胶植筋的应用范围将越来越广泛．目前，实际工程中无机胶植筋锚固深度通常采用 15 d或植筋胶生产商提供的建议值，未充分考虑各种锚固条件的影响，植筋结构的安全性及可靠性有待通过理论分析予以保证．本文通过统计分析大量无机胶植筋拉拔试验数据，利用一次二阶矩法（FOSM）对其进行可靠度分析，提出了无机胶植筋锚固长度的设计方法，对于无机胶植筋的工程应用具有现实意义．

1 极限状态方程和统计分析

1.1 极限状态方程

混凝土植筋在拉拔力作用下的失效主要表现为：钢筋屈服和粘接锚固破坏．当植筋的锚固长度处于临界锚固长度（lacr）时，粘接锚固破坏与钢筋屈服同时发生，锚固力的大小决定于钢筋的屈服强度（fy）及平均粘结锚固强度（τu）．由此，极限状态方程可表示如下：

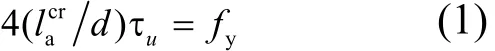
式中：lacr为临界锚固长度；d为钢筋直径；τu为平均极限粘结锚固强度；fy为钢筋的屈服强度．

根据大量试验数据的统计回归，无机胶植筋的极限粘结应力采用下式表示[8]：

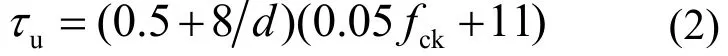
式中：d为钢筋直径（mm），fck为混凝土立方体抗压强度（MPa）．试验中实测的粘接锚固强度uτ,e可与利用式（2）计算得到的计算值ucτ,进行比较，经统计可得ueτ,/ucτ,的平均值为0.995 1，方差2σ为0.017 7，变异系数δ为0.133 7．将（1）式采用通用形式表示：

式中：R为锚固抗力，与锚固长度、钢筋直径和粘结强度有关；S为作用效应，即植筋的拉拔力．

1.2 统计资料

1.2.1 钢筋的屈服强度

根据文献[8]的试验统计结果，钢筋的变异系数δfy=0.069 9，钢筋的屈服强度按现行《混凝土结构设计规范》取其标准值 fyk，按 95%保证率求得的HRB335级钢筋屈服强度的平均值为：

1.2.2 基体混凝土抗拉强度

根据文献[9]得混凝土抗拉强度ft的统计参数如表1所示．

表1 混凝土抗拉强度参数统计(MPa)Tab.1 The tensile strength of concrete statistical parameters

1.2.3 几何尺寸

构件几何尺寸偏差统计参数见表2．

表2 构件几何尺寸偏差统计参数Tab.2 The geometry size deviation statistical parameters

1.2.4 计算模式的准确性

计算模式的准确性为试验实测值τu,e与试验回归统计值τu,c的比值，按以下公式计算：

由文献[8]试验资料统计得：平均值μΩp＝0.995 1，变异系数 δΩp＝0.133 7．

2 可靠度指标

为充分利用钢筋的极限承载能力，无机胶植筋的失效应保证使锚固钢筋达到屈服强度，而不是发生粘接锚固破坏．因此，锚固失效概率 Pfa应是钢筋应力超过屈服强度事件与锚固力小于屈服力事件同时发生的概率，即：

根据文献[10]，对于安全等级为二级的结构构件，取锚固承载力可靠度指标为βa＝3.95，相应失效概率Pfa＝4.0×10-5．钢筋应力达到屈服强度时的可靠指标β＝3.2，相应允许概率Pf＝6.87×10-4．因此，粘结锚固应力达到极限（τ=τu）事件的允许概率Pf0为：

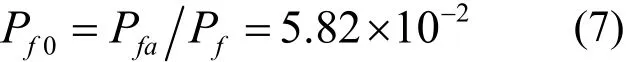
相应的可靠度指标β01＝1.57．

3 可靠度分析

本文采用一次二阶矩法（FOSM）中的中心点法对无机胶植筋进行可靠度分析．极限状态方程式（1）中各变量为相互独立的随机变量，式（3）中的R和S均为服从正态分布的综合变量，无机胶植筋的锚固长度 lacr可以通过一个方程式求解．结合前述分析可得：

效应S的特征参数：由公式（1）、（3）得效应的平均值 μS＝μfy，变异系数 δS＝δfy．

抗力的一般表达式为：

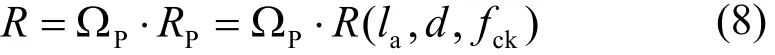
式中：ΩP为反映计算公式准确性的系数；RP为按给定公式计算所得的抗力；R（·）为抗力函数．

根据粘结锚固强度公式(2)，极限状态方程(1)及抗力表达式（8），有：

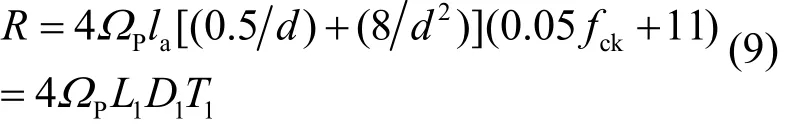
计算可得抗力R的统计参数为：

平均值

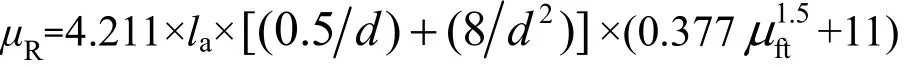
变异系数

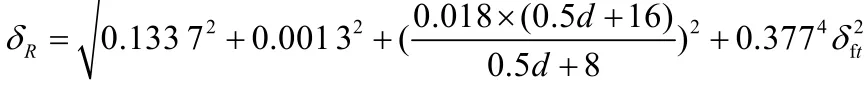
随机变量S、R均可认为服从对数正态分布，由可靠度指标表达式可得出计算锚固长度的方程式为：

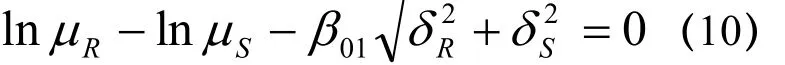
代入相应的统计参数为：

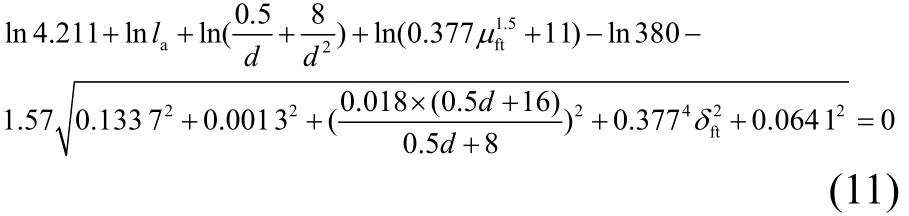
以不同的混凝土强度、不同的钢筋直径代入上式，即可得到在一定可靠度下各种直径钢筋在不同基体混凝土上的锚固长度的可靠度计算值如表3所示．

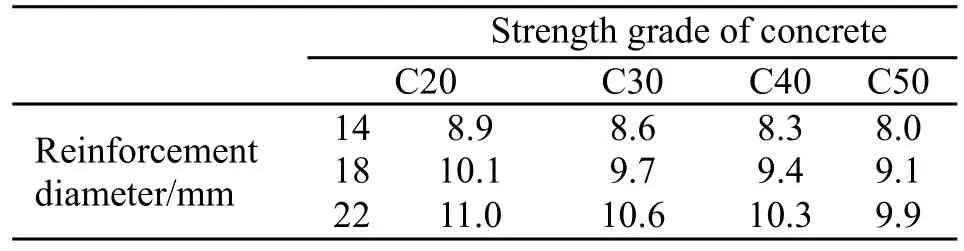
表3 无机胶植筋锚固长度的可靠度解（la/d）Tab.3 Reliability solution of inorganic adhesive anchorage length

为直观显示混凝土强度及钢筋直径对无机胶植筋锚固长度的影响，将常用钢筋直径及混凝土强度等级的可靠度计算值绘于坐标图中，如图1所示．

图1 钢筋直径及混凝土强度对锚固长度的影响Fig.1 Effects of diameter of reinforcement and concrete strength on the anchorage length

从图1可以看出，钢筋直径越大、混凝土强度越低，无机胶植筋所需的粘接锚固长度越长．

4 无机胶植筋锚固的设计建议

文献[1]给出了弹性剪切模式下的极限拉拔力和锥体高度的计算公式，但是计算较为复杂，不利于实际应用．因此，为使植筋设计与我国现行的“混凝土结构设计规范”相协调，本文建议无机胶植筋锚固长度采用均匀剪切模式方法，通过考虑不同锚固条件的影响进行简化计算．

4.1 基本锚固长度

采用无机胶植筋的受拉钢筋的基本锚固长度按下式计算：

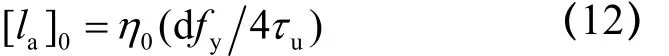
式中：fy为钢筋的设计强度（MPa）；d为钢筋直径（mm）；η0为考虑可靠度的安全系数，取 1.45；τu为在不同基体砼强度时所测得的植筋胶的极限粘结强度（MPa），本文采用式（2），并将其中的砼强度标准值改为设计值，即:τu= ( 0.5 + 8 d ) (0.05 fc+ 1 1)．

4.2 锚固长度的修正

不同锚固条件下的无机胶植筋的受拉钢筋的锚固长度按下式[11]计算：

式中：η1为结构重要性系数，安全等级为一级时，η1＝1.1；安全等级为二级时，η1＝1.0；安全等级为三级时，η1＝0.9；η2为钢筋类型影响系数，光圆钢筋η2＝2.25，带肋钢筋η2＝1.0；η3为钢筋锚固位置影响系数，一般取 η3＝1.0，不利时取 η3＝1.3；η4为加载方式影响系数，静载情况下取η4＝1.0，动载情况下取η4＝1.2．

5 算例

以安全等级为二级、采用Ⅱ级钢筋、锚固位置不利、且为动载情况时为例，无机胶植筋锚固长度的设计值如表4所示．

表4 锚固长度的设计值（la/d）Tab.4 Design value of anchorage length (la/d)

由算例可以看出，实际工程中所采用的植入深度为15 d基本满足设计要求，但并不合理，无机胶植筋的锚固长度应综合考虑不同锚固条件的影响．

6 结论

本文首先列出了无机胶植筋的锚固极限状态方程及有关的统计资料，进而对无机胶植筋进行了可靠度分析．在可靠度分析的基础上，本文采用均匀剪切模式方法进行简化，综合考虑不同锚固条件对无机胶植筋锚固长度的影响，给出了锚固长度合理实用的设计公式．主要结论如下：

（1）钢筋直径越大、混凝土强度越低，无机胶植筋所需的粘接锚固长度越长．

（2）实际工程中所采用的植入深度为15 d基本满足设计要求，但并不合理．

（3）本文提出的设计公式综合考虑了不同锚固条件的影响，对混凝土结构无机胶植筋的设计和施工具有现实的指导意义．

References

[1] 高天宝,杨树标,吴斌. 混凝土植筋设计的两种剪切模型[J].煤炭工程,2006(5): 75-78.GAO Tianbao, YANG Shubiao, WU Bin. Two kinds of shear model of bonded rebar design [J].Coal Engineering,2006(5): 75-78.

[2] 欧阳坚.混凝土加层框架节点抗震及建筑结构胶植筋的试验研究[D].南京:东南大学,2001.OUYANG Jian. Experimental study on reinforced concrete frame node seismic and bonded rebar [D].Nanjing:Southeast University, 2001.

[3] 周新刚.混凝土植筋锚固性能分析[J].岩石力学与工程学报, 2003,22(7):1169-1173.ZHOU Xingang. Anchorage behavior of post-embedded bars in concrete subjected to tension [J]. Rock Mechanics and Engineering, 2003, 22(7):1169-1173.

[4] 黄维民.温度作用下植筋锚固试件拉拔试验研究[D].长沙:中南大学,2010.HUANG Weimin. The drawing experimental study of bonded rebar under temperature [D].Changsha: Central South University, 2010.

[5] RONALD A Cook, JACOB Kunz, WERNER Fuchs, et al.Behavior and Design of Single Adhesive Anchors under Tensile Load in Uncracked Concrete [J]. ACI Structural Journal, 1998, 95( 1): 9-25.

[6] 刘向华. 植筋粘结锚固性能的试验研究及可靠度分析[D].合肥:合肥工业大学,2004.LIU Xianghua. The Experiment Study on Bonded Anchor Behavior of Planted Bar and Reliability Analysis[D].Hefei:Hefei University of Technology,2004.

[7] 姜常玖. 无机胶植筋式后锚固连接的抗火性能研究[D].济南:山东建筑大学,2013.JIANG Changjiu. Experimental study on fire behavior of the inorganically post-installed rebar connection [D]. Jinan:Shandong Jianzhu University, 2010.

[8] 高天宝. 混凝土结构无机料植筋拉拔试验研究[D].邯郸:河北工程大学, 2005.GAO Tianbao. The research on planting bars with inorganic material in concrete [D].Handan: Hebei University of Engineering, 2005.

[9] 赵更歧.植筋粘接锚固性能的试验研究[D].郑州: 郑州大学, 2001.ZHAO Gengqi. Experimental study on the anchorage performance of bonded rebar [D].Zhengzhou: Zhengzhou University. 2001.

[10] 赵国藩, 曹居易, 张宽权.工程结构可靠度[M]. 北京:科学出版社,2011.ZHAO Guofan, CAO Juyi, ZHANG Kuanquan. Reliability of engineering structure [M]. Beijing: Science Press,2011.

[11] 邵卓民, 沈文都, 徐有邻.钢筋砼的锚固可靠度及锚固设计[J].建筑结构学报,1986(6):36-49.SHAO Zhuomin, SHEN Wendu, XU Youling. The Reliability and Design for Anchorage of Reinforcing Bars[J].Journal of Building Structures,1986(6):36-49.