激光导引AGV的转弯算法研究

唐 瑞，颜文俊

(浙江大学电气工程学院，浙江杭州310027)

0 引言

自动导向小车(简称AGV［1-3］)是移动机器人的一种，是现代制造企业物流系统中的重要设备，主要用来储运各类物料，为系统柔性化、集成化、高效化运行提供重要保证［4］。

自动引导车的应用范围广泛，种类多式多样，按不同的标准可以有不同的分法，按照引导技术可以分为电磁引导、光条纹引导、磁带引导、超声波引导、激光引导和视觉引导等类型。其中激光引导式AGV 依靠激光扫描器发射激光束，然后接收由运行路径沿途墙壁或支柱上安装的高反光性定位标志反射回的激光束，计算出车辆当前位置及运动方向，再通过和内置的数字地图比对来校正方位，完成作业任务［5］。按照驱动方式可以分为单轮驱动、差速驱动和全方位驱动。单轮驱动AGV 往往是三轮式，前轮既是驱动轮，也是转向轮，两个后轮是从动轮［6］。

激光引导单轮驱动后叉式AGV 应用十分广泛，几乎可以替代传统叉车的所有功能［7］。这种AGV 主要的生产厂家有国内的云南昆船、沈阳的新松等。但其转弯速度都很慢而且转弯精度不高。因此通过研究精确度高、运行速度快的转弯算法，不仅可以提高AGV的运行速度，也可以提高整个行业的效率和经济效益。

本研究的对象是一种激光导引单轮驱动后叉式AGV 小车，其控制核心是西门子PLCS7-300。通过对其运动模型的建立和转弯误差的理论分析，同时结合Matlab 平台的仿真模拟，最后再通过实验验证。本研究提出一种弯道预补偿和直线矫正相结合的转弯算法，通过实际测试验证其有效性。

1 AGV 小车的结构及运动模型

1.1 AGV 小车的结构

AGV 小车的结构如图1所示。

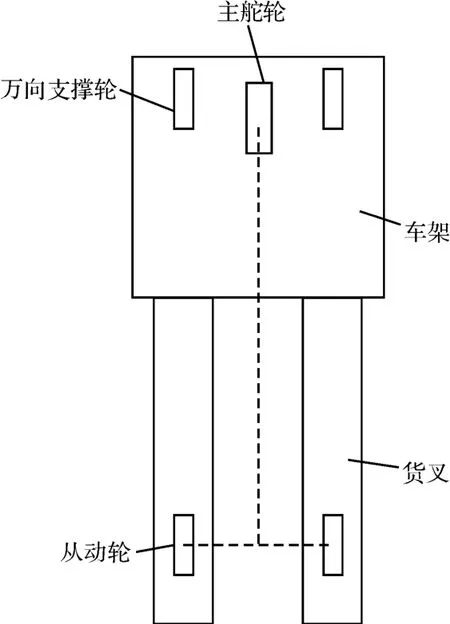
图1 AGV 小车结构示意图

AGV 小车采用单舵轮结构，主要包括1 个主舵轮和2 个从动轮，以及若干个万向辅助支撑轮。其中主舵轮既是驱动轮也是转向轮，分别由直行伺服电机和转弯伺服电机进行驱动。从动轮被固定在货叉支撑体的下部，只能前、后方向滚动。主舵轮与从动轮的相对位置与布局方式决定了AGV 的运动学模型，而万向辅助支撑轮对模型的建立没有影响［8-9］。

1.2 AGV 小车的运动学模型

为了建立小车的运动学模型，本研究做出3 个假设:①车体关于纵向轴线严格对称，且重量相等;②运行场地的表面保持水平，车轮与表面始终保持接触;③车轮始终做滚动运动。

AGV 小车的运动学模型如图2所示。

根据几何关系可以求得:

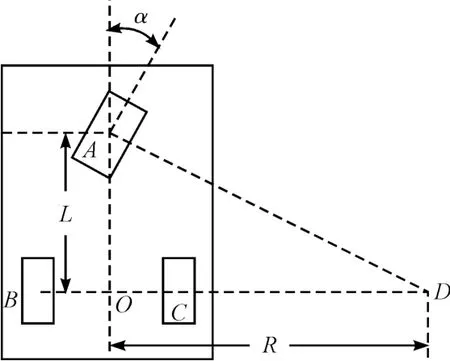
图2 AGV 小车运动学模型

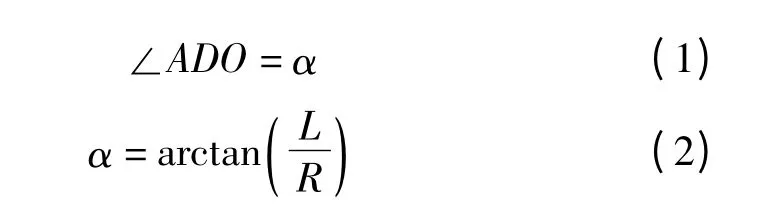
AGV 小车在做直线运动时即前行或者后退时其运动学模型与图2 类似，只是α=0°，导引算法一般采用成熟的PID 控制算法。AGV 小车做直线运动时，其运动学模型的基本方程很简单，只要进行X 坐标或者Y 坐标与目标坐标的比较，所以其控制算法结构简单，运行速度快，控制精度高。

AGV 小车在走圆弧轨道时，转弯伺服电机需要控制主舵轮转动一个角度。根据小车所走的圆弧轨道的半径不同，由式(2)可知，转弯伺服电机需要控制主舵轮转动的角度就会不同。由于物理规律的限制，转弯伺服电机控制的主舵轮不能瞬间转到所需的角度，需要一个加速减速的过程。在主舵轮转弯的同时AGV小车一直在运动。所以这里就会存在很大的误差，从而导致AGV 小车偏离目标圆弧。本研究就是通过研究AGV 小车转弯时误差，找出其规律，然后通过预先补偿来减少甚至消除小车的圆弧误差。下一节就这个问题进行讨论。

2 AGV 转弯时的误差分析及补偿

2.1 AGV 小车的参数

本研究实验用的AGV 小车的各项参数如下:车长L=1.365 m;主舵轮的最大转角α = ±20°;转弯伺服电机的最大转速为2 800 r/min;减速比为200;设转弯伺服电机的加速时间为0.05 s，所以主舵轮的最大转角速度ω=2 800 ×2 ×π/60/200;最大角加速度δ=ω/0.05。

2.2 AGV 小车主舵轮转弯过渡段分析

为了方便分析，本研究把主舵轮的转弯过程进行离散化，离散化曲线如图3所示。

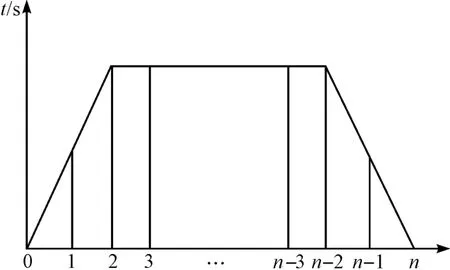
图3 主舵轮转弯过程离散化曲线

设主舵轮由0°转到所需的角度α 的运行时间为t，以0.025 s 为周期将时间t 分为n 段，并且设转弯伺服电机的加速和减速过程都采用最大角加速度δ，则主舵轮的加、减速段分别被分为2 段。加速段取距离本段起点时间2/3 处时间值为本段的时间参数;减速段取距离末端时间点2/3 处的时间点作为本段的时间参数;匀速段时间参数则选取本段中点的时间值作为本段的时间参数［10］。

主舵轮加速和减速过程转过的角度如下式所示:

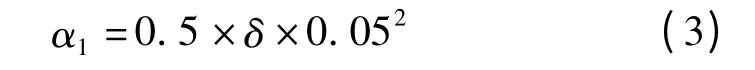
主舵轮匀速段转过的角度如下式所示:

主舵轮匀速转动的时间如下式所示:

每一段运行时间如下式所示:

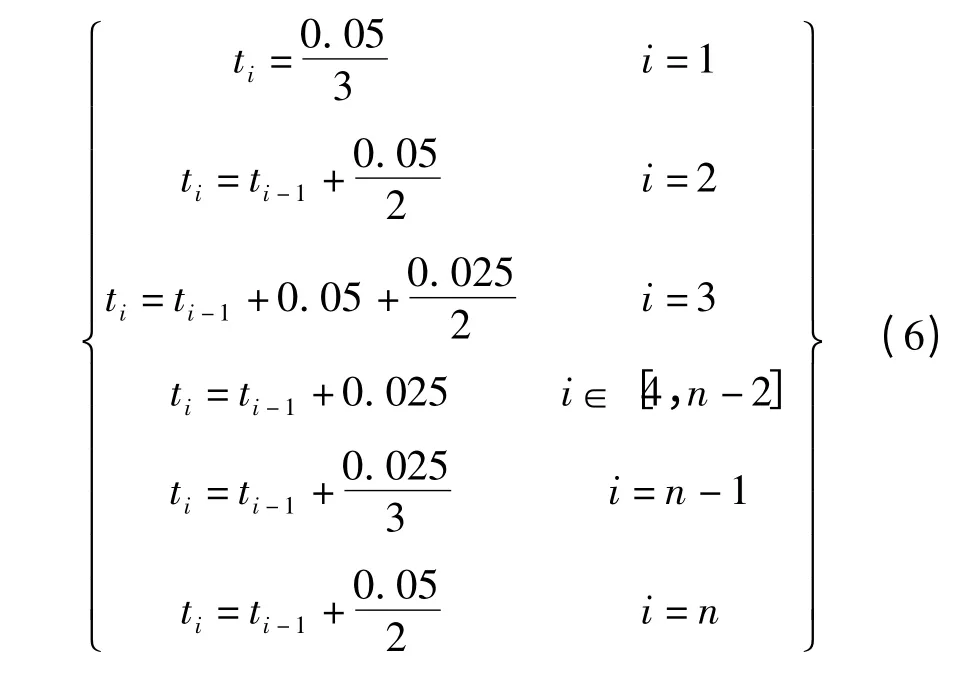
主舵轮转过的角度值如下式所示:

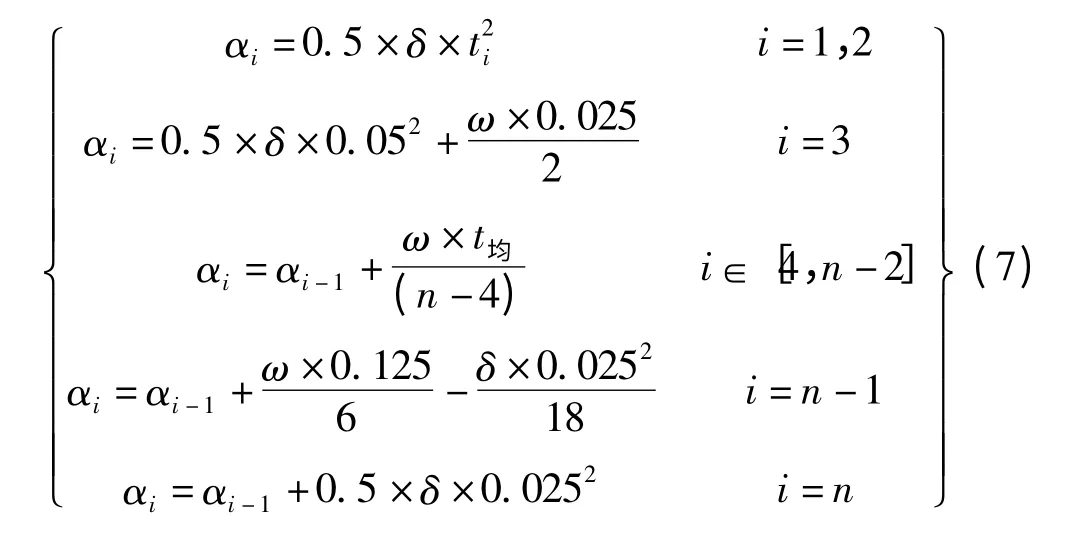
每段时间内AGV 小车的弯道半径如下式所示:

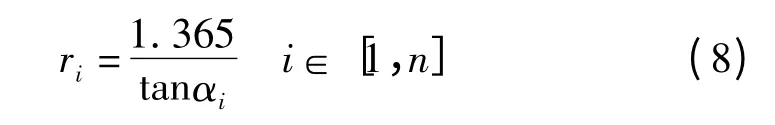
AGV 的角速度如下式所示:

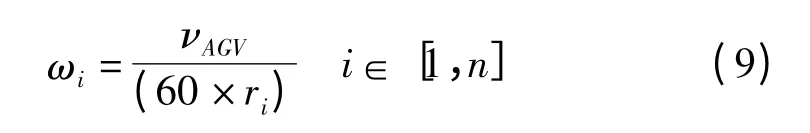
AGV 转过的角度增量如下式所示:

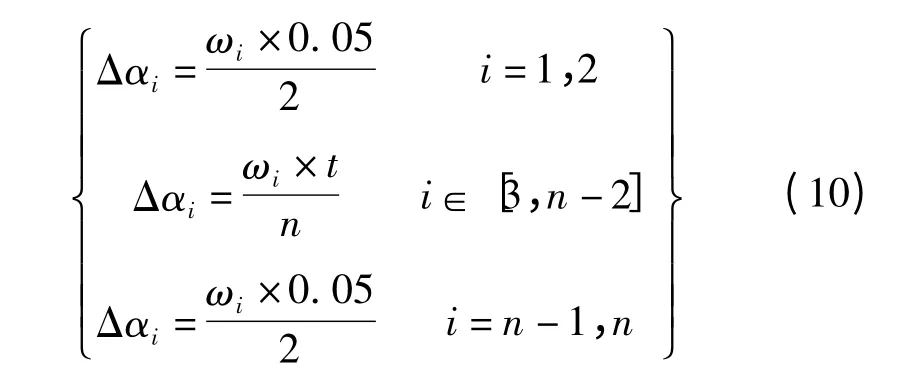
AGV 转过的角度如下式所示:

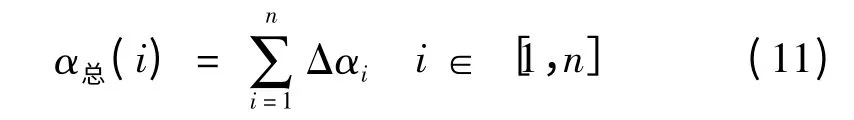
每一段x 的增量如下式所示:

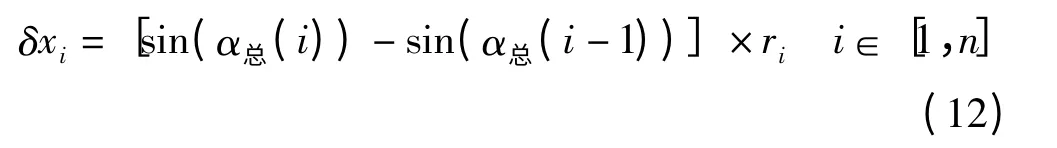
每一段y 的增量如下式所示:

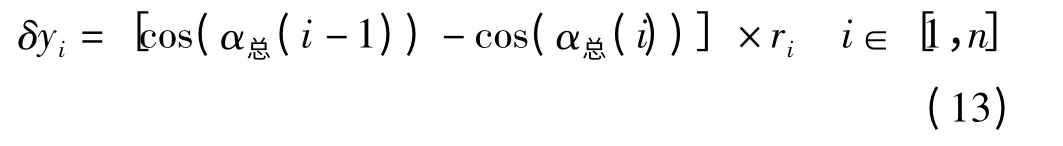
通过上面的主舵轮转弯过程离散化分析可知，AGV 小车从直行状态进入弯道时，因为主舵轮转到目标角度需要时间。在这段时间内AGV 小车还在前进，从而造成AGV 小车偏离目标圆弧轨迹。

本研究采用预先弯道补偿和直行矫正相结合的方法来减少甚至消除弯道误差，其基本的思路如下:转向轮转到目标角度需要一定时间，在此期间小车一直在向前运动，这段时间就是造成小车弯道误差的原因，本研究是通过让小车提前转弯，当小车转向轮转到目标角度值时，这个坐标点刚好就在目标轨迹上，从而减小小车的弯道误差。小车需要提前的转弯的直线距离结合2.2 节弯道过渡过程的分析可以计算得到，具体的分析见下一节的特例仿真。

3 仿 真

为保证预先弯道补偿方法的可靠性，本研究在AGV 小车允许的转弯半径范围中，随机取一个数值比如r=2 m 来进行仿真分析，同时设小车进入弯道的车速为20 m/min。

取0.025 s 为采样时间，主舵轮的角速度变化图如图4所示。主舵轮转到目标角度所花费的时间图如图5所示。

因为本研究采用的实验AGV 小车，是物流行业中经常使用的后叉式AGV，它的转弯圆弧轨迹一般都是四分之一段圆弧，所以本研究在仿真时为了贴合实际，设AGV 小车需要转过的是一段0°到90°半径是2 m的圆弧轨迹，圆弧的起点坐标为x =0，y =0，圆弧的终点坐标为x=2，y=2。

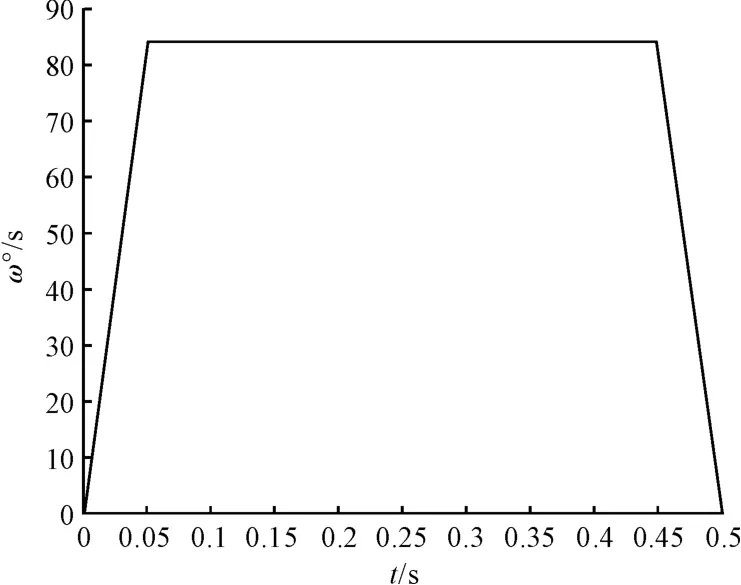
图4 主舵轮的角速度曲线图

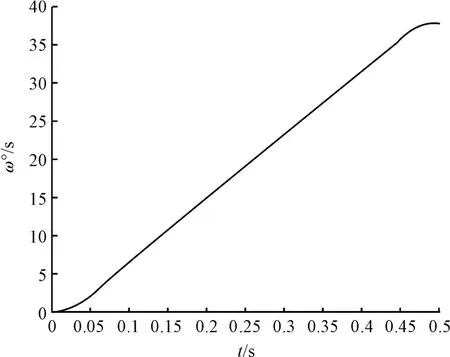
图5 主舵轮的角度变化曲线图

本研究在Matlab2013a 中进行弯道补偿前和补偿后AGV 小车转弯的圆弧轨迹的对比，AGV 运行轨迹图如图6所示。

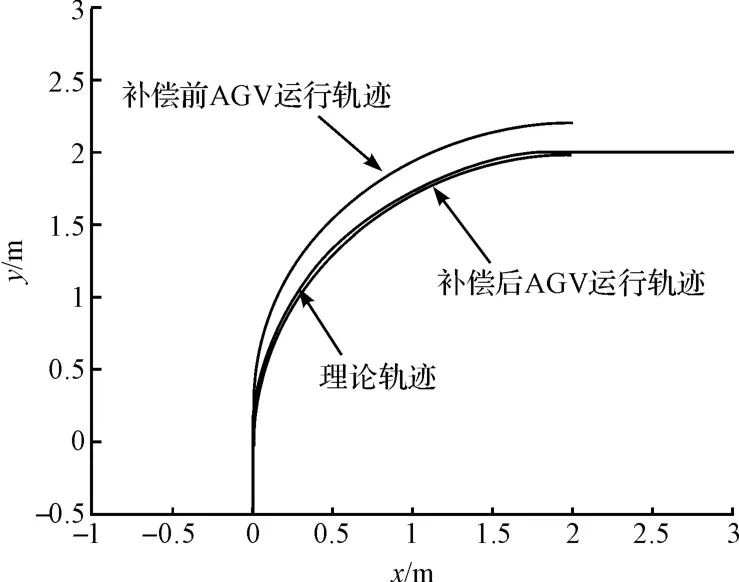
图6 AGV 运行轨迹图

代入式(2)计算可得，AGV 小车的主舵轮需要转动的目标角度为34.313 5°，由图5 可知主舵轮转到目标角度需要0.458 5 s。代入2.2 节的转弯过程计算公式后，可得AGV 小车转到目标角度时的车身坐标为(0.086 2，0.126 2)，结合图6 可知，此时的圆心坐标为(2.086 2，0.126 2)，整个圆弧沿y 轴正方向移动了0.126 2 m，明显偏离目标轨迹。

结合主舵轮的转弯角度和AGV 小车进入弯道的车速采用的弯道预补偿算法，小车提前转弯的距离为0.13 m，AGV 运行轨迹图如图6所示，经过补偿后的AGV 小车圆弧轨迹和目标轨迹的误差很小。经过计算可得终点坐标误差为3 mm，满足AGV 小车的误差要求。

4 现场实验

为了验证弯道预补偿算法的实际效果和其运行速度，本研究在研究所自主研发的激光引导后叉式AGV小车上进行了实验验证，AGV 小车的实物如图7所示。

图7 实验平台

本研究设置AGV 小车需要转过的目标圆弧轨迹的半径为2 000 mm，圆弧的起点坐标为:(1 500，3 000)，终点坐标为:(3 500，5 000)(单位是mm);小车分别以不同速度进入弯道。

为了保证实际实验结果的有效性，本研究所做的30 次实验，都是在同一块场地，从相同的起点开始转弯。

本研究从30 组实验数据中，选取了12 组有代表性的实验数据，如表1、表2所示。

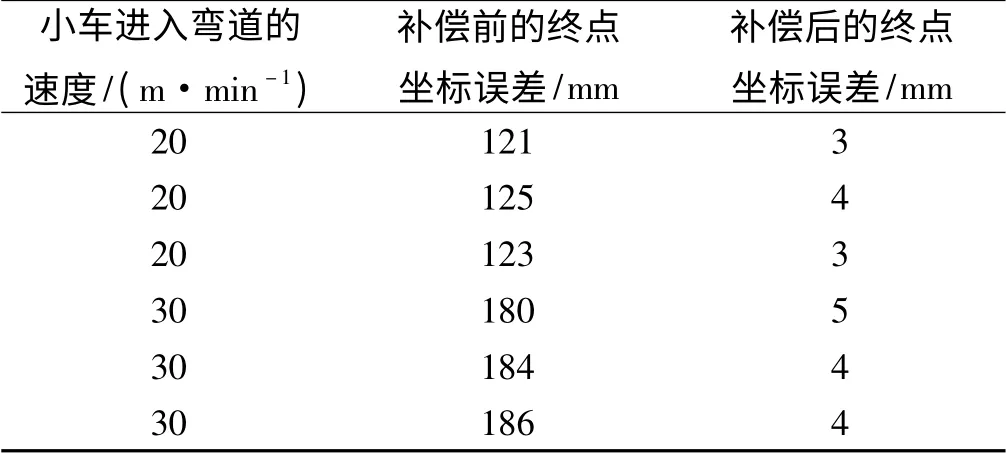
表1 不同弯道速度下AGV 小车转弯精度

由表1 可以看出，经过弯道预补偿后，AGV 小车的转弯精度有了明显的提高，同时在提高车速的情况下，小车的转弯精度也能满足要求。

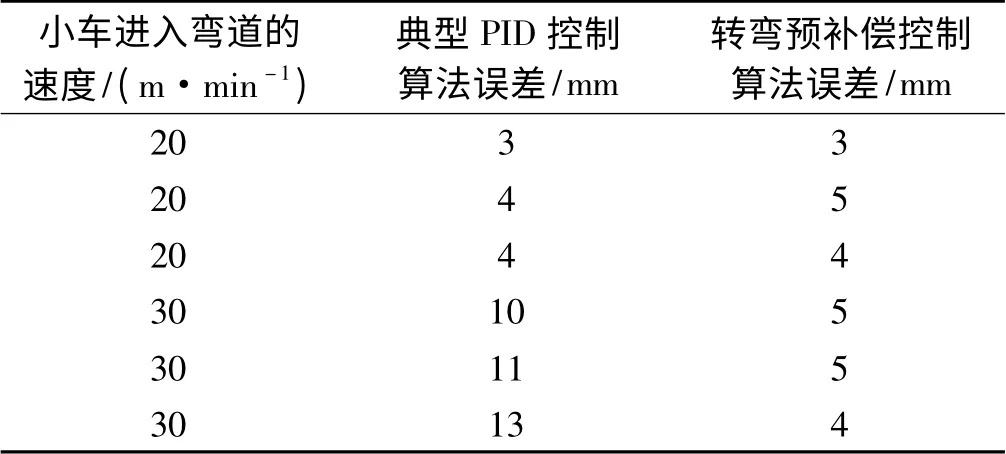
表2 不同转弯控制算法下AGV 小车的转弯误差

由表2 分析可知:AGV 小车在低速入弯时，比如速度为20 m/min 时，弯道预补偿算法的弯道控制精度与经典的PID 算法控制精度基本相同;当AGV 小车入弯速度提高到30 m/min 时，弯道预补偿算法的精度反而优于经典的PID 控制算法。

经过分析可知:该实验使用的AGV 小车的控制核心是西门子PLCS7-300，其CPU 的运算速度一般，当小车高速入弯时，经典PID 弯道控制算法因自身的复杂程度高，对PLC 的运算速度要求增高，从而造成控制精度下降;弯道预补偿算法因其结构简单，对PLC 运算能力要求不高，所以当AGV 小车入弯速度提高时，其控制精度仍然满足要求。

但是弯道预补偿算法的高精度是通过移动圆弧轨迹的圆心实现的，所以AGV 小车的入弯速度不能太高;当实际情况要求很高的转弯速度时，可以通过弯道预补偿算法和直行矫正相结合的方式来达到要求。具体的流程如下:适当降低转弯精度，当小车进入随后的直线运行时，通过直行引导算法消除误差。之所以上面的结合控制方式可行，是因为直行引导算法结构简单，不需经过复杂的几何运算，运算速度快控制精度高，能迅速地矫正前一段弯道的误差。

5 结束语

本研究对单轮驱动转向型AGV 进行了运动学分析，在对其转弯误差分析的基础上，提出了弯道预补偿算法，并进行了仿真分析和实验验证。实验结果表明，该控制算法可以在满足弯道精度的前提下，提高AGV弯道速度。可以为常规的生产提供理论参考。

在下一阶段，本研究将通过大量实验来进一步确定AGV 小车的理想弯道速度。同时由于弯道速度的增加，最终的误差可能不满足要求，因此在今后的研究中，需要进一步改进弯道预补偿算法，减少误差，达到更好的控制效果。

［1］HAMZHEEL M，FARAHANI R Z.An ant colony-based algorithm for finding the shortest bidirectional path for automated guided vehicles in a block layout［J］.International Journal of Advanced Manufacturing Technology，2013，64(1-4):399-409.

［2］SOK Y L，HAI W Y.Navigation of automated guided vehicles using magnet spot guidance method［J］.Roboticsand Computer-Integrated Manufacturing，2012，28(3):425-436.

［3］YING C H，TA W L.Zone design and control for vehicle collision prevention and load balancing in a zone control AGV system［J］.Computer ＆ Industrial Engineering，2009，56(1):417-432.

［4］刘 波，汪宇辰，梁伟健，等.基于MC9S12XS128MAL 控制的光电导引式AGV［J］.机电工程，2013，30(7):837-838.

［5］朱天宇，谭 琳.激光导引四轮驱动型AGV 小车模糊控制的研究［J］.机电工程，2013，30(8):1026-1028.

［6］范 堃.自动导引车车载系统研究与实现［D］.杭州:浙江大学电气工程学院，2013.

［7］李占贤，冯永利.单舵轮AGV 路径跟踪控制器设计［J］.控制工程，2014，5(21):70-71.

［8］耿牛牛.单舵轮AGV 路径跟踪方法的研究［J］.制造业自动化，2011，33(4):81-82.

［9］沈 颖.激光导引AGV 车载控制系统研究［D］.合肥:合肥工业大学机械与汽车工程学院，2007.

［10］赵玉麟.单轮驱动/转向AGV 轨迹分析及视觉导航［D］.西安:西安理工大学机械电子工程学院，2006.