基于FPGA的磁悬浮微驱动器控制系统研究*

杨莉莉，郭 亮

(浙江理工大学机械与自动控制学院，浙江杭州310018)

0 引言

微驱动器是指能产生精度较高的驱动力器件或装置，其作为微机电系统(MEMS)的核心部件，广泛存在于微小机器人的活动关节、微小航天仪器、磁盘驱动、超精密加工等方面，因此对微驱动器的测量控制研究显得尤为重要［1-2］。由于传统的接触式、气浮式微驱动器难以在定位精度、运动自由度等方面实现更高的设计要求，磁悬浮式微驱动器以其优越的定位性能受到了广泛关注，并在精密微小领域获得了更大的发展。磁悬浮微驱动器系统是一个非线性、参数摄动、耦合、抗干扰能力差的精密复杂系统［3-4］，对于动子多自由度的运动控制是由单个自由度运动控制结合而成的，因此完成动子多自由度精确定位的重要基础是动子的无静差稳定悬浮。

本研究主要实现对磁悬浮微驱动器悬浮状态的精确控制，传统控制系统中常采用PC 或DSP 进行控制，PC 控制系统中外部数据采集卡的采样频率较低，难以满足高速数据处理的要求，进而无法实现高精度控制的目的;DSP 运算速度快，合适处理密集的加乘运算［5］，但用户可自定义管脚过少，不利于实现对多相电机的控制。而FPGA 以其高时钟频率著称，不仅内部延时小，能并行运行程序完成大量数据运算，而且扩展性较好，便于后续控制系统功能的升级［6-7］，经过综合分析比较后，选择型号为EP2C5T144I8 的FPGA 作为主控芯片，用于实现磁悬浮微驱动器的悬浮系统控制。

本研究针对日磁悬浮微驱动器的实时精确控制问题，对FPGA 的磁悬浮微驱动器进行了研究。

1 磁悬浮微驱动器

1.1 磁悬浮微驱动器结构

层叠绕组式磁悬浮微驱动器的结构如图1所示，它由背铁、塑胶板、空心绕组及定子永磁阵列等4 部分组成。其中:定子部分的永磁体采用二维Halbach 的永磁矩阵结构，该矩阵由形状尺寸完全相同的109 块钕铁硼材料制成的永磁体模块和12 块铁块组成，动子部分采用层叠式空心绕组的结构，四层绕组正交叠加，自上而下的四层导线中第一、三层沿y 方向铺设，第二、四层沿x 方向铺设［8］。

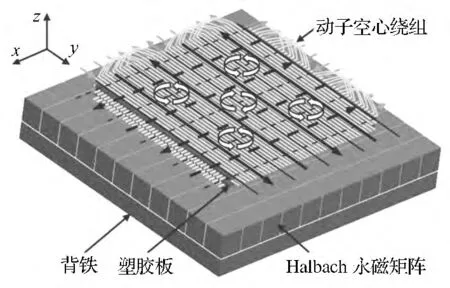
图1 磁悬浮微驱动器结构

1.2 磁悬浮微驱动器工作原理

动子线圈采用相互间隔的直导线的形式排列，通过改变动子导线中的通电电流的大小和方向，即可改变动子导线板受到的洛仑兹力，从而改变动子的悬浮状态。

本研究以图1 中最底层的沿x 方向排列的直导线为对象进行分析，该层动子导线板与永磁体的位置关系如图2所示。相邻实线之间的导线电流方向相同，磁场为水平方向。笔者将水平充磁磁块上方虚线间的绕组设置为悬浮力控制绕组，其余绕组则设置为水平推力控制绕组;改变悬浮力控制绕组的电流即可实现动子直导线板的悬浮定位和绕x 轴旋转，而改变水平力控制绕组的电流即可实现其y 方向的平动，同理可对y 方向排列的空心绕组进行分析，并由此得出结论。通过控制绕组中的电流可实现动子线圈5 个自由度的运动，分别为沿x、y、z 轴平移以及绕x 轴、y 轴旋转。

1.3 磁悬浮微驱动器动子运动模型

为了避免悬浮过程中动子线圈其他自由度方向的运动，本研究利用滚珠直线轴承把动子线圈固定在4根垂直杆上，使其只能进行z 方向运动。通过对动子线圈的电流控制调整后使得每根导线中电流元受到的洛伦兹力方向向上。以动子导线板的位移、运动速度以及电流为变量，根据洛伦兹力、电路原理以及运动学相关原理可知，悬浮微驱动器动子的运动模型如下:

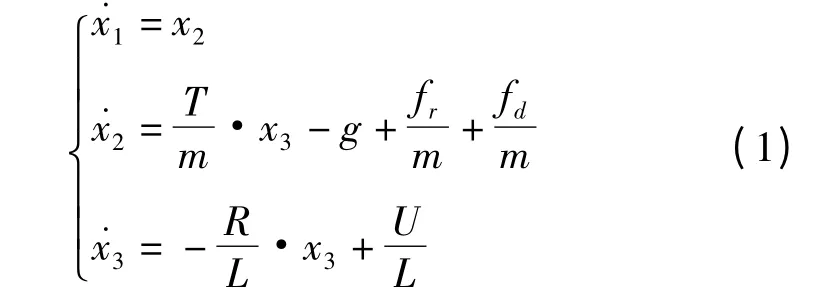
式中:T—磁场强度;g—重力加速度;fr—动子导线板所受的摩擦力;fd—系统所受到的外部干扰;l—磁场中每根导线的长度;m—动子导线板质量，其值为313.36 g;R—单根导线电阻，其值为0.7 Ω;L—直导线形成的等效电感，其值为84.3 μH;U—系统输出的控制电压。

2 PID 控制仿真

PID 控制通过对误差进行比例、积分、微分调节，具有参数调整方便、结构简单、稳定性好等优点［9］。为减小计算过程中产生的误差，本研究对PID 算法进行离散化后分别得到第k 次和第k－1 次控制算式，两式相减后得到增量型PID 控制算法公式如下式所示:

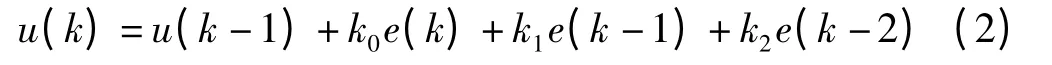
式中:KP、Ki、Kd—比例、积分、微分环节对应的参数，系数k0= Kp+ Ki+ Kd，k1=－ Kp－2Kd，k2= Kd，e(k)、e(k－1)和e(k－2)分别为第k、k－1 和k－2 次测量偏差。

笔者通过Matlab 对微驱动器运动模型进行PID控制仿真，其仿真模型如图3所示。结合Signal Constraint 调节PID 参数，仿真出的PID 参数为KP=10.986 1，Ki=2.704 3，Kd=0.070 7，PID 参数下系统的1 mm阶跃响应仿真波形如图4所示。仿真结果的超调为4%，整定时间0.06 s，稳态误差小于1%。

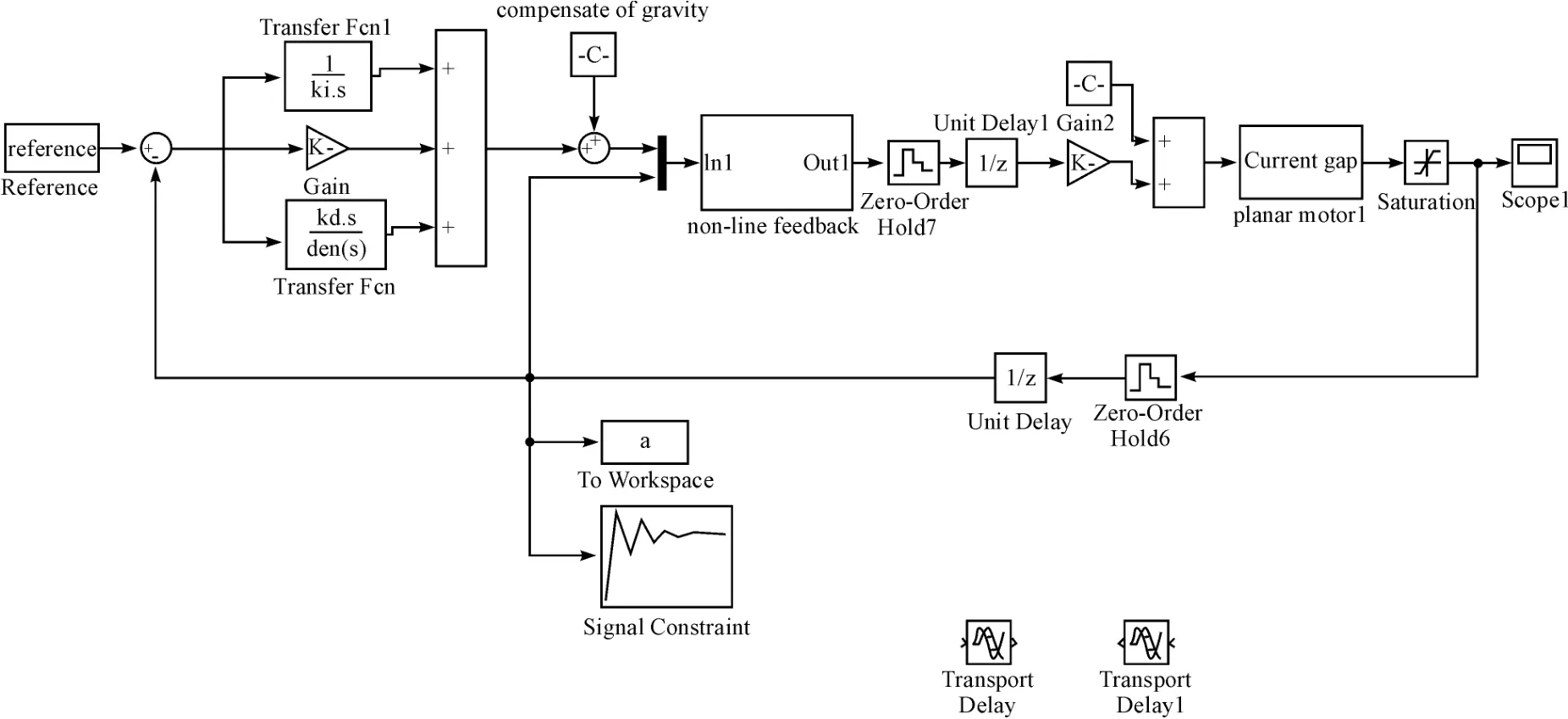
图3 PID 控制仿真模型

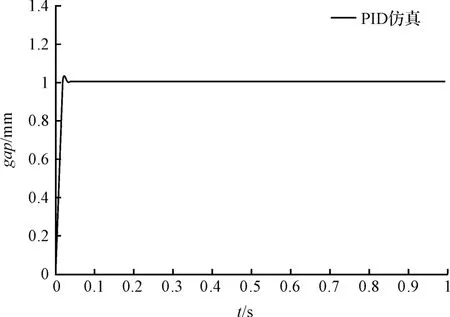
图4 PID 仿真波形

3 控制系统硬件设计

为实现动子无静差悬浮和快速响应，需设计硬件系统将采集到的动子悬浮气隙高度转化为电压信号，经过数据处理后将控制信号传输给动子线圈，从而实现整个系统的闭环控制。控制系统选用涡流传感器KD2306-2S1 测量动子悬浮高度，输出的位移信号经A/D 转化为数字量后传输至FPGA 中，数字信号在FPGA 中完成滤波算法，通过电压转换后完成PID 控制算法，最后由FPGA 将控制信号发送给DA 并输出至驱动器，从而完成驱动平面电机动子的工作。同时需要将采集到的电压信号传输至PC 机并转化成动子线圈的悬浮高度，实时显示在上位机界面上，观察响应时间、超调量、波动等信息，验证控制效果。系统硬件框图如图5所示。

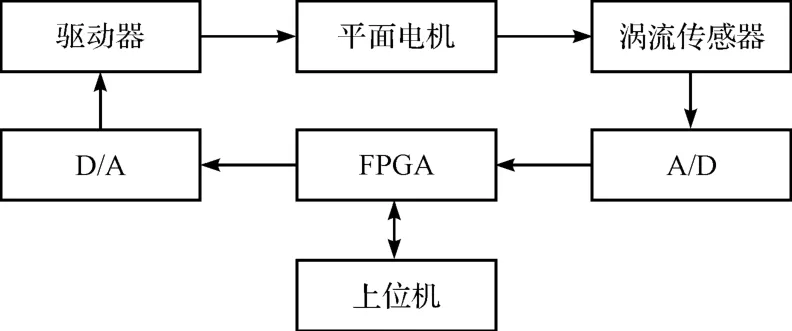
图5 系统硬件框图

3.1 A/D 采样电路

A/D 采样电路中使用的ADC 芯片AD7671AST 为16 位逐次逼近式高精度模数转换器，其最高采样速率可达1 MSPS。为了驱动AD7671 且保持其SNR 和转换噪声的性能，选择低噪声、高增益带宽的OP07AZ 作为输入缓冲器，并接入10 pF 的外部补偿电容。2.5 V参考电压由电源转换芯片ADR421 提供。OVDD 输入引脚设置为数字3.3 V 以匹配FPGA 的端口电压［10-11］。

(1)WARP 和IMPLUSE 配置为低电平，使AD7671工作于NORMAL 模式;

(2)SER/PAR 配置为低电平，使采样电路输出16位并行信号;

(3)采集的微驱动器悬浮信号的范围为－10 V ～10 V，依据模拟输入配置表将INA 接参考电压REF，INB、INC 接模拟地、IND 接模拟输入;

(4)CS、CNVST、RD、BUSY 控制引脚和16 位DATA 数据引脚分别与FPGA 各引脚相连，完成AD7671的采样过程。

3.2 DA 数据输出电路

DA 芯片选用16 位串行高速数模转换芯片AD5545，为了输出±5 V 的信号，DA 输出口外接高精度运算放大器AD8620，运算放大电路中选用0.01%精度的电阻以提高输出精度。FPGA 通过CS、RS 及LDAC控制信号将数据从SDI 引脚输出至DA，完成驱动控制。

4 控制系统软件设计

FPGA 内部逻辑控制模块主要包括ADC 采样模块、FIFO［12］模块、滤波模块、PID 控制模块、DAC 数据输出模块及RS-232 通信模块，FPGA 逻辑控制软件的整体框图如图6所示。

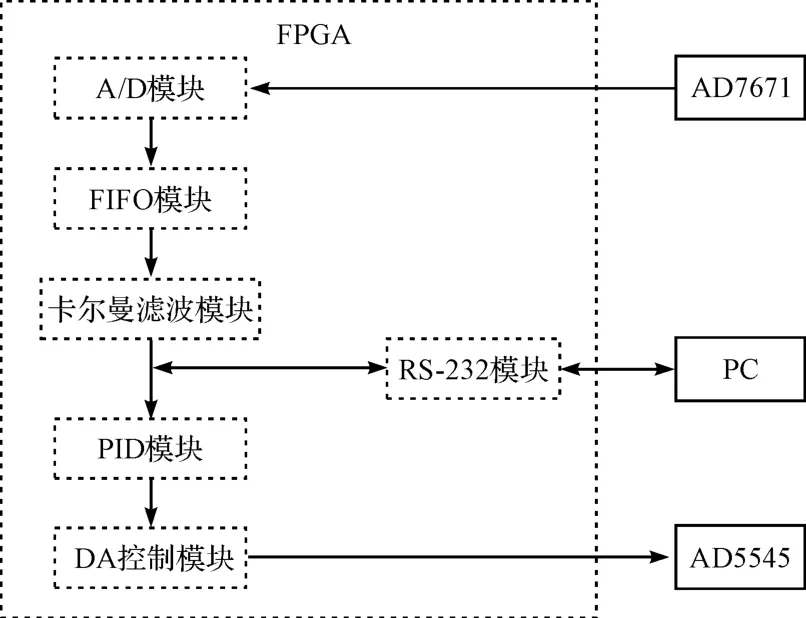
图6 软件控制系统框图

4.1 A/D 采样控制模块

A/D 采样时序由FPGA 控制产生，而时钟信号由AD7671 内部自己产生。CNVST 低电平时启动转换，完成信号读取，两个时钟周期后使CNVST 为高电平，进入数据保持阶段，BUSY 为AD7671 的反馈信号，一旦A/D 开始转换，则变为高电平，在BUSY 为高电平时选通RD 并读取上一次转换数据。状态机初始状态为S0，此时RD 和CS 为高电平状态，CNVST 为低电平，将CS 变为低电平，CNVST 变为高电平后，进入S1状态，即开始模数转换，等待1 个时钟周期后进入S2状态判断BUSY 是否为高电平，是则进入S3 状态，将RD 变为低电平，并开始读取转换结果;否则继续等待，读取完成后返回S0 状态。

4.2 FIFO 缓存模块

为解决A/D 数据采集速度和后续卡尔曼滤波器运算速度匹配问题，本研究通常在中间加入FIFO 缓存器。FIFO 缓存模块为四级缓存，该模块分别检测写信号和读信号，检测到写使能信号且寄存器未满时，将数据保存至寄存器，同理，检测到读使能信号时完成从寄存器中读取数据。

4.3 卡尔曼滤波模块

卡尔曼滤波是用一组递归方程组来估计系统的状态。卡尔曼滤波方法计算速度快，占用内存少，满足磁悬浮控制系统实时性的要求，当信号和噪声同时输入时，卡尔曼滤波器能在保留信号的同时，最大程度抑制噪声［13］。卡尔曼滤波算法步骤如下:

(1)设置系统初始估计值X0，初始均方误差阵P0和初始信号值Zk;

(2)由式(4)计算出预测误差Pk|k－1;

(3)再根据式(5)计算出滤波增益Kk;

(4)将数据代入(3)可得最优预测值Xk|k－1;

(5)最后根据以上数据通过式(7)计算出最优滤波估计值Xk，同时根据公式(6)更新Pk的值。

通过步骤(1)～(5)完成了一次滤波周期算法，卡尔曼滤波计算公式如下:

(1)最优预测值:

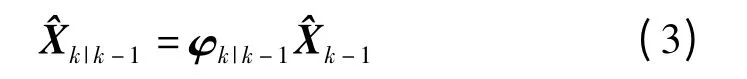
(2)预测误差协方差:

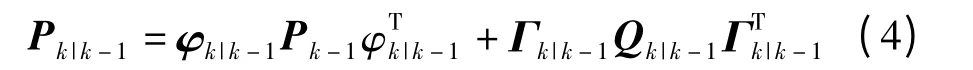
(3)滤波增益矩阵:

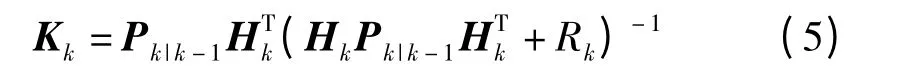
(4)估计误差协方差:

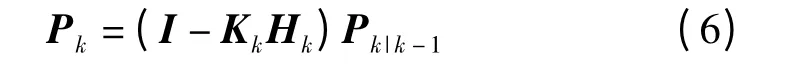
(5)最优滤波估计值:

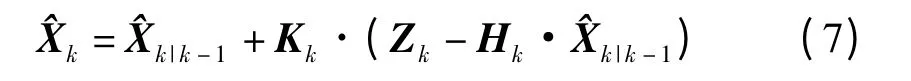
4.4 PID 算法控制模块

PID 算法选择并行方式实现，采用增量式算法将PID微分方程分解为FPGA 易实现的基本运算式，以便于将运算器和数据类型进行归一化处理，达到减少运算算子的目的。对并行结构方法进行改进的运算思路如下:

(1)减法运算通过二进制补码形式实现，即A－B=A+(B 补);

(2)扩展加法运算位数，同符号数相加时可能出现运算结果位数溢出，因此在数据运算中将数据结果扩展一位;

(3)由于FPGA 不支持浮点运算，故将浮点数转换成定点数进行运算;

(4)FPGA 只能进行整数运算，为保留采样数据的精度，计算时需要将实数转换为整数，即将数据扩大10n使小数转化为整数，计算后再使输出结果缩小10n作为输出信号;

(5)寄存器REG 可锁存信号，3 路信号并行计算减少了延时时间，提高了运算的速率。

笔者根据公式(2)对期望值r(k)与测量值y(k)的偏差e(k)进行PID 运算，其中系数k0、k1、k2均由仿真得出，与改进后的并行结构共需要4 个加法器、3 个乘法器，比传统并行结构少用了3 个减法器，不仅减少了连线数量，且提高了对设计的加法IP 核的利用率，降低了设计的难度，提高了工作效率。

4.5 DA 控制模块

DA 控制输出状态机初始状态为S0，此时CS =0，LDAC=0;CS 与LDAC 均变为高电平后，进入S1 状态;CS 上升沿触发DAC 输入，将包括地址信号在内的18 位数据传输至DAC 内部的输入寄存器中，然后进入S2 状态，此时计数器开始从0 ～18 的计数，保证DAC 完成输入寄存器的数据串行移位至DAC 寄存器;改变CS 和LDAC 的电平，使CS 和LDAC 变为低电平，进入S3 状态，完成数模转换并输出。

4.6 RS-232 通信模块

FPGA 与上位机通信采用RS-232 通信方式，波特率设定为9 600，即接收一个bit 的时间为1 s/9 600 =104 μs。由于FPGA 的晶振为50 MHz，故可用50 M 时钟设计计数器，并根据计数器发送数据，一次完整数据接收需要有1 144 000 ns，所以计数器必须计满57 200次，所以需要16 位计数器。由于A/D 采样得到的数据为16 位，而RS-232 一次最多传送8 位，本研究将16位数据分成两部分，高、低8 位依次经过RS-232 与上位机通信。

5 实验及结果分析

为验证磁悬浮控制系统的可行性，笔者搭建实验平台。磁悬浮平台的动子表面积略大于永磁体，边长大约为120 mm，动子板的4 个角通过滚珠式直线轴承与竖直导轨相连，使动子只产生z 方向位移，导轨上安装涡流传感器对悬浮高度进行实时测量，控制信号通过驱动器线性放大后转化为微驱动器动子绕组的输入电流信号，调节动子导线板与定子永磁体间相互作用的电磁力从而控制动子悬浮高度，上位机中实时显示控制效果。磁悬浮控制实验系统框图如图7所示。

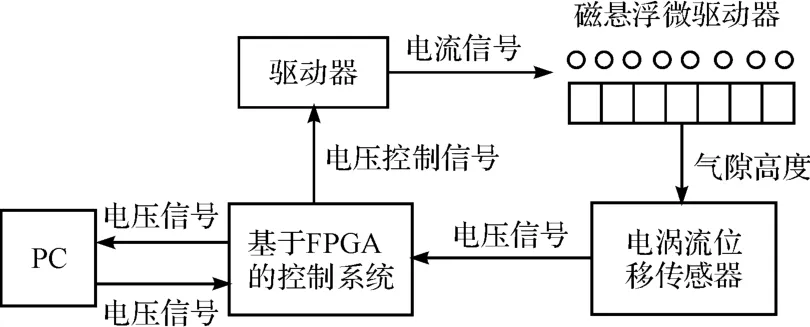
图7 磁悬浮控制实验系统框图

在PID 控制器下的磁悬浮系统的1 mm 阶跃响应实验图如图8所示。系统频率为10 kHz，通过分析曲线可知该系统的超调量为4.2%，整定时间为0.05 s，系统的稳态误差为1 μm，与图4 仿真结果基本一致。

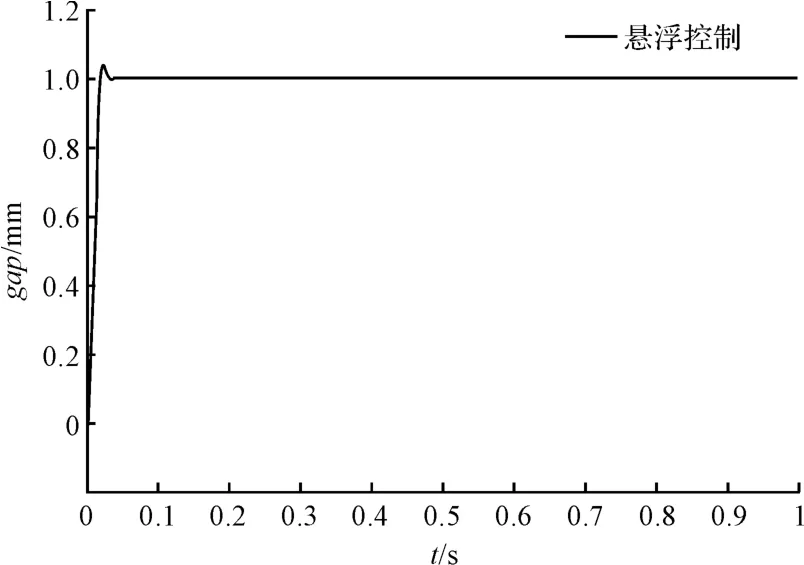
图8 PID 控制下系统阶跃图

验证磁悬浮控制系统的控制精度，控制系统在1 mm和1.7 mm 气隙高度下1 μm 位移的多次阶跃响应图形如图9所示。从图9 中可以看出系统能快速作出反应且波动范围在1 μm，基本能够实现定位精度为1 μm的大范围精确控制。

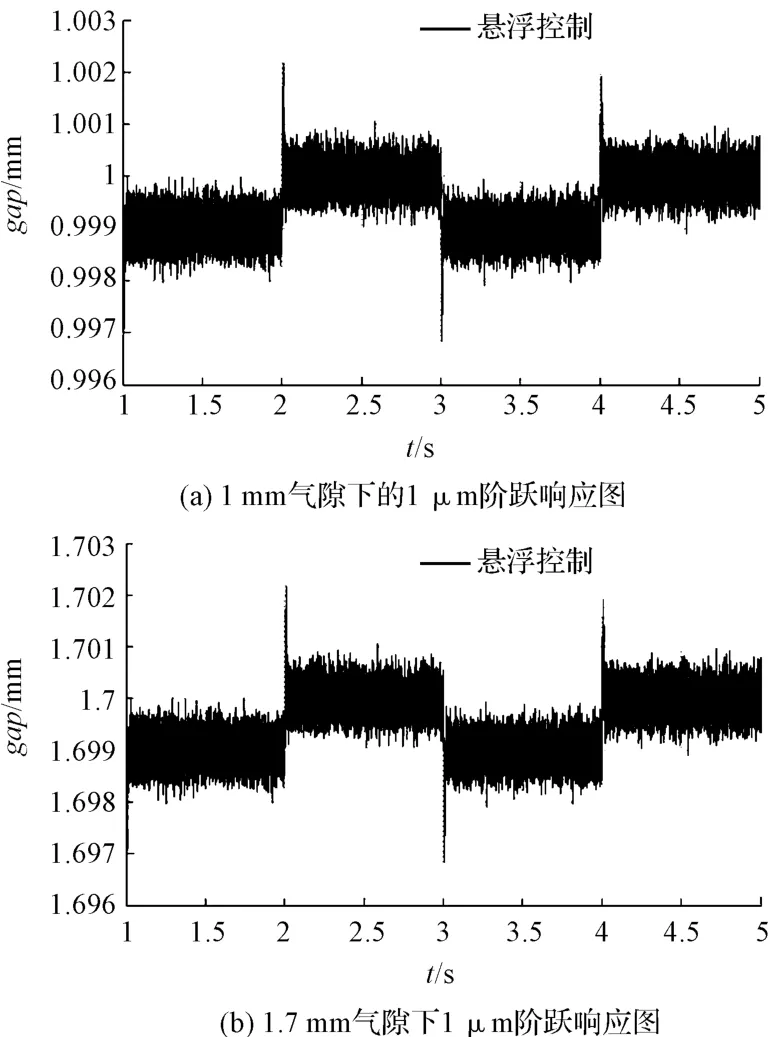
图9 1 μm 阶跃响应

然后验证磁悬浮系统在PID 控制下的运动跟踪能力，在1 mm 气隙下对正弦目标信号的跟踪实验结果如图10所示，系统对峰-峰值为20 μm，频率为10 rad/s 的正弦信号跟踪图如图10(a)所示，可看出系统符合预期曲线，跟踪效果较好，对峰-峰值为2 μm，频率为10 rad/s的正弦信号跟踪图如图10(b)所示，可以看到动子运动图形与预期正弦信号基本一致，并具有优良的实时性。

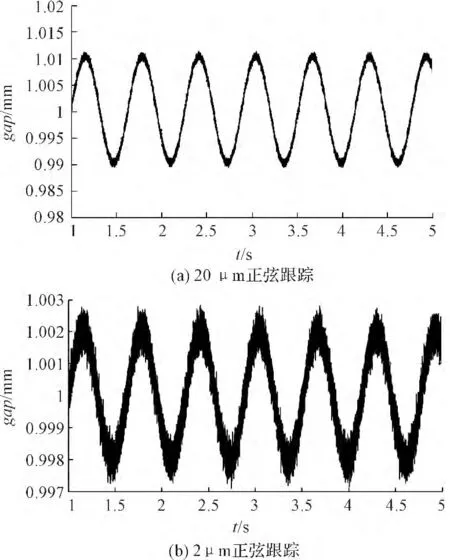
图10 正弦跟踪响应

6 结束语

该设计的硬件电路能对磁悬浮微驱动器悬浮运动模型进行精确的信号采集，PID 控制算法能切实有效地对悬浮信号进行闭环实时控制，通过搭建悬浮控制系统实验平台对磁悬浮微驱动器进行实时PID 控制实验，通过将控制系统仿真数据与实验数据进行对比可知，在1 mm 阶跃响应中，系统上升过程和稳态过程几乎完全相同，验证了运动模型的准确性。通过对不同气隙下的连续阶跃响应和不同幅值的正弦跟踪响应图形可知，系统的反应速度快、跟踪范围大、跟踪延迟和跟踪误差小、控制精度高，实现了2 mm 范围内1 μm精度的悬浮微运动控制，在磁悬浮微驱动器微小定位方面有着良好的应用，为MEMS 的精密化方向发展垫定了基础。

［1］赵立敏.MEMS 微驱动器的设计、工艺及应用［D］.西安:西安电子科技大学机电工程学院，2014.

［2］周海波.磁悬浮直线运动系统的设计与控制研究［D］.湖南:中南大学机电工程学院，2010.

［3］仇志坚，戴 军，陈小玲.基于不完全微分PID 的斥力型磁悬浮平台控制系统研究［J］.微特电机，2014，42(10):75-77.

［4］CHEN J，YANG S.Design of magnetic levitation micro-actuator positioning control system［J］.Application of Electronic Technique，2012，38(3):96-98.

［5］侯正男，蒋启龙，刘 东.基于DSP 的交流磁悬浮稳定控制［J］.电力电子技术，2014，48(9):48-50.

［6］JASTRZEBSKO R，POLLANEN R，PYRHONEN O.Real-Time Emulator of Magnetic Suspension System for FPGAbased Controller［C］//Mechatronics，2006 IEEE International Conference on.IEEE，2006:98-103.

［7］柏 滢，林 都，鲜 浩.基于FPGA+DSP 的数据采集与实时处理系统的设计［J］.传感器世界，2014，20(10):27-31.

［8］张 钊.层叠绕组式磁悬浮永磁直流平面电机鲁棒控制系统研究［D］.浙江:浙江理工大学机械工程学院，2014.

［9］李垂君.基于FPGA 的PID 控制器研究与实现［D］.辽宁:大连理工大学电子与信息工程学院，2008.

［10］李 苏，李 辉.基于AD7671 的声波采集电路设计［J］.石油工业计算机应用，2012(4):29-31.

［11］樊 凡，张 鹏.高精度模数转换器AD7671 的原理及应用［J］.今日电子，2004(9):57-58.

［12］XIAO J.Implementation of asynchronous FIFO buffer based on FPGA［J］.Electronic Measurement Technology，2009，32(11):92-94.

［13］周 倩.车辆组合导航中卡尔曼滤波器的设计及FPGA实现［D］.北京:北京交通大学电子信息工程学院，2009.